题目

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：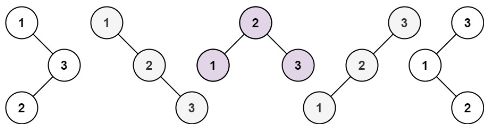
image.png

  1. 输入：n = 3
  2. 输出：5

示例 2：

  1. 输入：n = 1
  2. 输出：1

提示：

  • 1 <= n <= 19

    解题方法

    动态规划

    定义动态数组dp[i]表示i个节点能够组成的二叉搜索树的数量。
    对于节点总数为n的情况，根节点左右子树的节点和为n-1，设其左右子树节点数目分别为l和r，则有：
    96. 不同的二叉搜索树 - 图2
    因此递推关系如下：
    96. 不同的二叉搜索树 - 图3
    时间复杂度O(n^2)，空间复杂度O(n)
    C++代码：

    1. class Solution {
    2. public:
    3.   int numTrees(int n) {
    4.       int dp[20] = {0};
    5.       dp[0] = dp[1] = 1;
    6.       for(int i=2; i<=n; i++) {
    7.           for(int j=0; j<i; j++) {
    8.               dp[i] += dp[j]*dp[i-1-j];
    9.           }
    10.       }
    12.       return dp[n];
    13.   }
    14. };

    数学推导

    上述递推公式生成的数组称为 卡塔兰数。其递推公式如下：
    96. 不同的二叉搜索树 - 图4
    时间复杂度O(n)，空间复杂度O(1)。
    C++代码：

    class Solution {
public:
  int numTrees(int n) {
      long long result = 1;
      for(int i=0; i<n; i++) {
          result = result * 2 * (2*i+1) / (i+2);
      }

      return result;
  }
};