题目

给你一棵二叉树的根节点 root，返回其节点值的 后序 遍历 。

示例 1：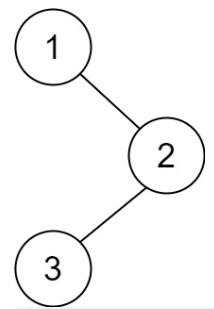

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

• 树中节点的数目在范围 [0, 100] 内

• -100 <= Node.val <= 100

  
  进阶：递归算法很简单，你可以通过迭代算法完成吗？

  解题方法

  递归

  迭代遍历二叉树，先后处理左子树、右子树、再将父节点压入数组。
  时间复杂度O(n)，空间复杂度O(logn)，最劣O(n)
  C++代码：

  /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
  class Solution {
  public:
    void post_order(TreeNode* p, vector<int>& vec) {
        if(p != nullptr) {
            if(p->left != nullptr)   post_order(p->left, vec);
            if(p->right != nullptr)  post_order(p->right, vec);
            vec.push_back(p->val);
        }
    }
  
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
  
        post_order(root, result);
  
        return result;
    }
  };
  

  迭代

  采用先序遍历的方式，调整顺序使遍历顺序为 中右左，随后反转数组即可。
  时间复杂度O(n)，空间复杂度O(logn)，最劣O(n)
  C++代码：

  /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
  class Solution {
  public:
    void post_order(TreeNode* p, vector<int>& vec) {
        stack<TreeNode*> nodes;
        if(p != nullptr) nodes.push(p);
        while(nodes.size()>0) {
            TreeNode *tmp = nodes.top();
            nodes.pop();
            vec.push_back(tmp->val);
            if(tmp->left != nullptr)   nodes.push(tmp->left);
            if(tmp->right != nullptr)  nodes.push(tmp->right);
        }
    }
  
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
  
        post_order(root, result);
        reverse(result.begin(), result.end());
  
        return result;
    }
  };
  

  Morris 遍历

  通过 Morris 遍历二叉树，在返回父节点后将左子树的最右节点支路压入数组，并将该段顺序反转。最后将从根节点到最右节点支路的全部节点压入数组，并反转。
  时间复杂度O(n)，空间复杂度O(1)。
  C++代码：

  /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
  class Solution {
  public:
    void add_nodes(TreeNode* p, vector<int>& vec) {
        int count = 0;
        while(p!=NULL) {
            count++;
            vec.push_back(p->val);
            p = p->right;
        }
        reverse(vec.end()-count, vec.end());
    }
  
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        TreeNode *mostright, *cur = root;
  
        while(cur != NULL) {
            mostright = cur->left;
            if(mostright != NULL) {
                while(mostright->right != NULL && mostright->right != cur)  mostright = mostright->right;
  
                if(mostright->right == NULL) {
                    mostright->right = cur;
                    cur = cur->left;
                }
                else {
                    mostright->right = NULL;
                    add_nodes(cur->left, result);
                    cur = cur->right;
                }
            }
            else {
                cur = cur->right;
            }
        }
        add_nodes(root, result);
  
        return result;
    }
  };
  

  标记法（二叉树遍历的统一写法）

  设置标志位来判别节点是否二次访问，对二次访问的节点压入数组。
  时间复杂度O(n)，空间复杂度O(logn)，最劣O(n)
  C++代码：

  /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
  class Solution {
  public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> nodes;
        if(root != nullptr)     nodes.push(root);
  
        while(nodes.size()>0) {
            TreeNode *tmp = nodes.top();
            if(tmp != NULL) {
                nodes.pop();
                nodes.push(tmp);
                nodes.push(NULL);
                if(tmp->right != nullptr)   nodes.push(tmp->right);
                if(tmp->left != nullptr)    nodes.push(tmp->left);
            }
            else {
                nodes.pop();
                tmp = nodes.top();
                result.push_back(tmp->val);
                nodes.pop();
            }
        }
  
        return result;
    }
  };