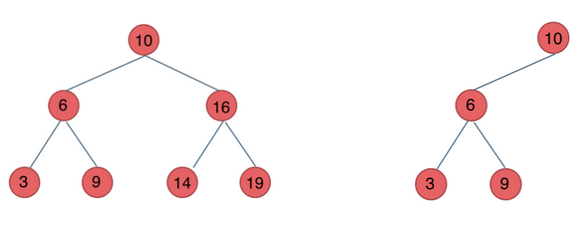
:::info 定义：是包含n个节点的有限集合，该集合或者为空集（此时，二叉树称为空树），或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。 :::

基本概念

树形结构

定义：每个节点连接若干个子节点的数据结构。
度：每个节点拥有的子节点数目
定理：在一个二叉树中，度为 0 的节点比度为 2 的节点多 1
二叉树：最大度为 2 的树形结构

二叉树的种类

二叉树主要分为两种形式：满二叉树、完全二叉树

满二叉树

定义：如果一棵二叉树只有度为 0 和 2 的节点，并且度为 0 的节点在同一层上，则这棵二叉树称为满二叉树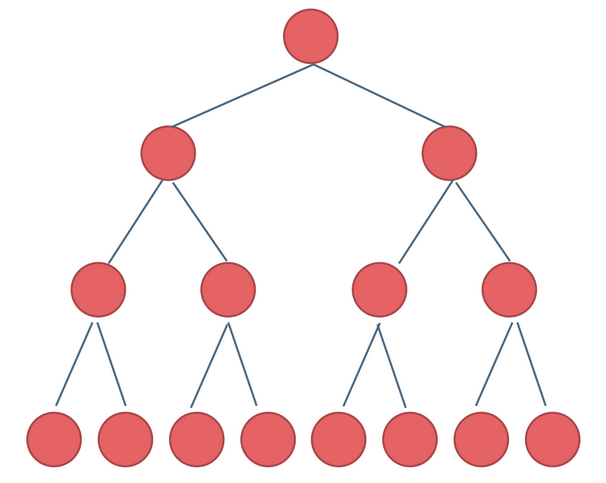
1.png
节点数目：对于深度为 k 的满二叉树，节点数为 2^k-1 个

完全二叉树

定义：除了最底层节点可能没填满外，其余层节点数均达到最大值，并且其下一层的节点都集中在该层最左边的若干位置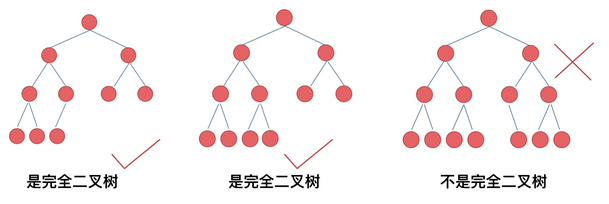
1.png 底层节点数目：设最底层为第 h 层，则该层包含 1~2^(h-1) 个节点
性质：完全二叉树的节点编号可计算、可使用连续的存储空间存储
节点编号：对于节点编号为 n 的节点，他的左子数根节点编号为 2n，右子树根节点编号为 2n+1

二叉搜索树

定义：节点有数值的二叉树，是一个有序数

  • 若左子树不为空，则左子树上所有节点的数值均小于根节点的数值
  • 若右子树不为空，则右子树上所有节点的数值均大于根节点的数值
  • 左、右子树也是二叉搜索树

1.png

平衡二叉搜索树

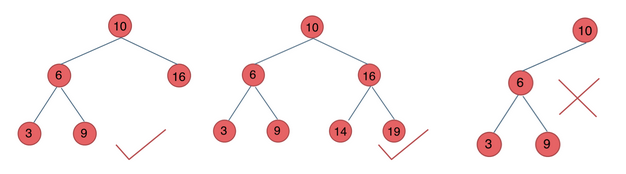
定义：AVL (Adelson-Velsky and Landis) 数，具有以下性质：

  • 一棵空树，或其左右子书的高度差绝对值不超过 1
  • 左右连个子树也都是平衡二叉树

1.png
C++中**map**、**set**、**multimap**，**multiset**的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是 logn
unordered_map、unordered_map底层实现是哈希表

二叉树的性质

  • 在二叉树中，第 _i_ 层上至多有 _2^(i-1)_ 个节点（i≥1）
  • 深度为 _k_ 的二叉树至多有 _2^k-1_ 个节点_（k≥1）_
  • 对一棵二叉树，如果叶子节点的个数为 _n_0，度为 2 的节点个数为 _n_2，则_n_0=_n_2+1

  • 具有 _n_ 个节点的完全二叉树的深度为⌊_log_2_n_⌋+1

    二叉树的存储方式

    二叉树可以通过链式存储，也可以通过顺序存储

    顺序存储

    顺序存储的二叉树通过数组实现，如下图
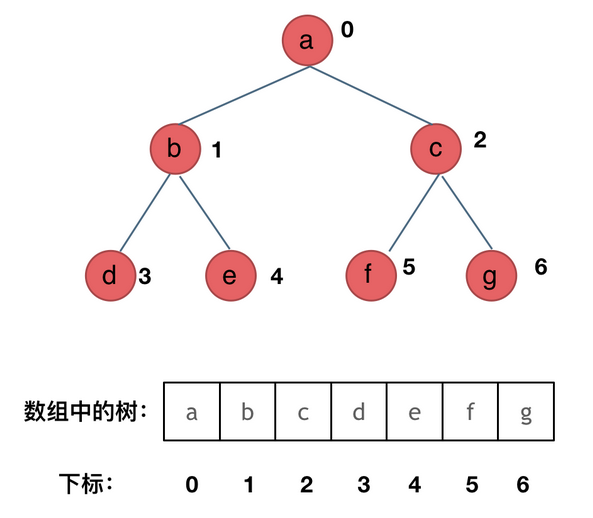    1.png 顺序存储中使用符号如'^'代表没有节点

    链式存储

    链式存储通过指针分别指向左右子树的根节点，实现如下

    1. struct TreeNode {
    2.   int val;
    3.   TreeNode *left;
    4.   TreeNode *right;
    5.   TreeNode(int x) : val(x), left(NULL), right(NULL) {}
    6. };

    二叉树的遍历

    二叉树的遍历方式分为深度有限遍历 (DFS) 和广度优先遍历 (BFS)
    深度优先遍历包括前序遍历、中序遍历、后序遍历，均可通过递归或迭代实现
    广度优先遍历包括层序遍历，只能通过迭代实现
    深度优先遍历中的顺序即中间节点的遍历顺序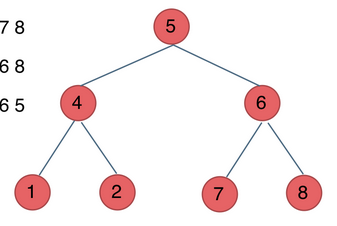
    1.png

    前序遍历

    方法：首先遍历父节点，再依次遍历左子树和右子树。
    遍历结果：5 4 1 2 6 7 8

    void pre_order(TreeNode *p) {
  if (p != NULL) {
      printf("%d\t", p->val);
      pre_order(p->left);
      pre_order(p->right);
  }
}

    中序遍历

    方法：先遍历左子树，再遍历父节点，最后遍历右子树
    遍历结果：1 4 2 5 7 6 8

    void mid_order(TreeNode *p) {
  if (p != NULL) {
      mid_order(p->left);
      printf("%d\t", p->val);
      mid_order(p->right);
  }
}

    后序遍历

    方法：先遍历左子树，再遍历右子树，最后遍历父节点
    遍历结果：1 2 4 7 8 6 5

    void post_order(TreeNode *p) {
  if (p != NULL) {
      post_order(p->left);
      post_order(p->right);
      printf("%d\t", p->val);    
  }
}

    中序遍历

    方法：逐层遍历节点
    遍历结果：5 4 6 1 2 7 8

    void lever_order(TreeNode *p) {
  list<TreeNode *> t;
  if (p!=NULL) {
      t.push_back(p);
  }

  while (t.size()>0) {
       printf("%d\t", (t.front())->val);
      if ((t.front())->left != NULL) {
          t.push_back((t.front())->left);
      }

      if ((t.front())->right != NULL) {
          t.push_back((t.front())->right);
      }

      t.pop_front();
  }
}