6.1 扩频码的同步
- 扩频码同步:
- 扩频码同步是指到达接收机的扩频编码信号与本地参考扩频信号,在码图案位置和码时钟速率,在时间上都是准确一致的。
- 扩频通信体制成败的关键性问题
- 扩频通信系统必不可少环节
- 对期望信号实现解扩和对非期望信号进行频谱扩展的关键
- 扩频码同步包含两个步骤:
- (1)同步捕获(Acquisition,粗同步):
- 使本地参考码与接收码的相位(延时)之差小于半个码元(切普)宽度,要求本地振荡中心频率精确到使解扩后信号频谱落在中频滤波器的通频带之内,保证解调器能很好地工作。
- (2)同步跟踪(Tracking,精同步):
- 同步捕获后,本地参考码必须尽可能精确跟踪接收信号的变化,使本地参考码相位与接收码相位的差别尽可能的小,以期在相关器获得最大相关输出。
- (1)同步捕获(Acquisition,粗同步):
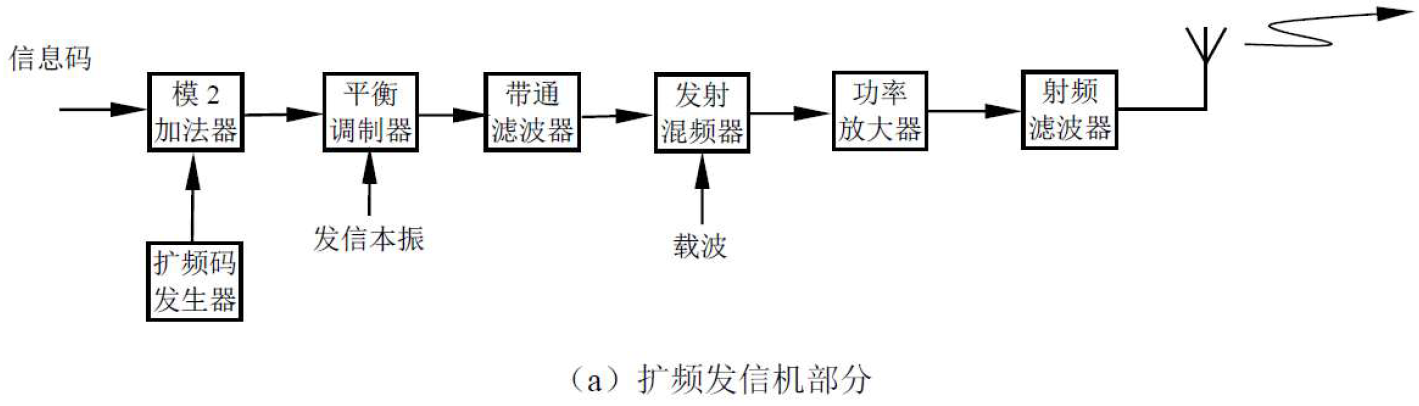
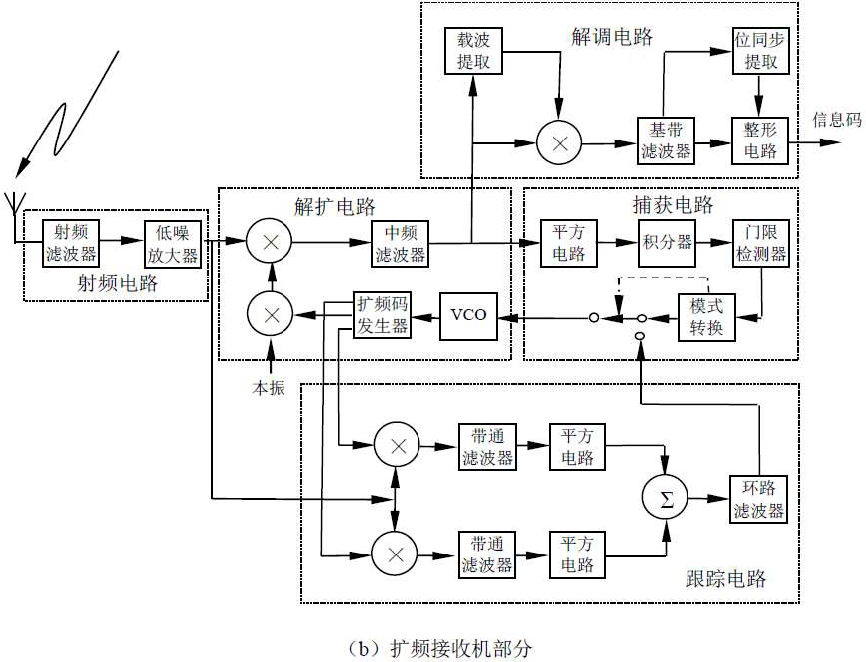
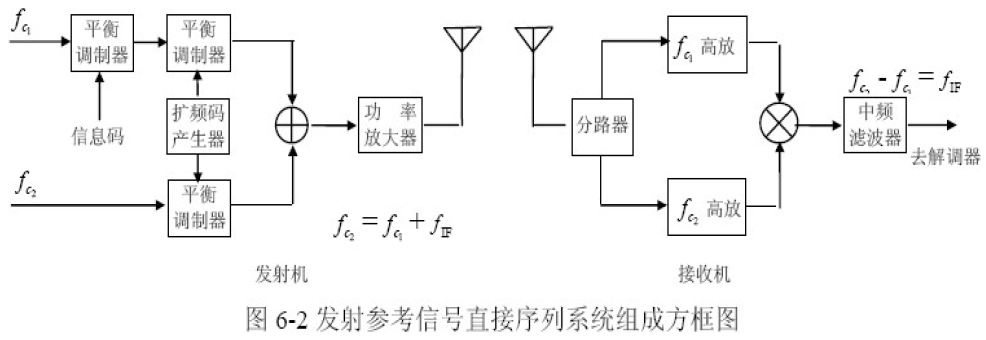
扩频码同步方法:
特点:
- 本地参考码由发射机产生,再发送到接收机。
- 扩频码同时对两载波进行调制,信息仅对载波
调制,两波相差一中频。
- 接收机混频后为已解扩的中频信号
- DS系统和频率FH系统都适用
特别适用于对接收机体积、重量和成本有严格限制的系统
(1)接收机简单
(2)抗干扰能力差
- 以降低系统抗干扰性能、加大接收机输出噪声或降低输出信噪比为代价
- 只要能进入接收机射频通道的两个频率差为
的干扰信号都能对接收机造成干扰,不受扩频处理增益抑制
- 接收机参考信号不是本地产生,而是经传输得到,在传输过程中必然会受到干扰或噪声的污染而使接收机输出噪声增大。
(3)效率低
- 从能量角度看,由于载波
不携带信息,对输出信噪比改善毫无贡献,浪费发射机功率资源。
- 从能量角度看,由于载波
(4)不适用于CDMA体制
卫星通信中广泛应用
- 在统一定时扩频通信系统中,可以采用像原子钟(铷钟,铯钟)那样准确度极高的时钟
- 若卫星轨道参数可以精确知道,传输延迟也可精确计算出来
- 接收机只要经过极短的搜索时间就可捕获接收到的扩频码信号,从而实现扩频码同步。
- 空间应用的原子时钟:
- 铯钟;精度最高、(2000万年差1 秒),GPS系统
- 铷钟
- 氢钟
对比石英晶体
- 误差每天不大于千分之一秒
原理
- 发射机发射一个短促的高功率低占空比脉冲信号,给接收机提供快速同步信息,告诉接收机随后而来的是DSSS信号或FHSS信号的起始相位(起始时间)
特点
自同步的理论依据:
- 基于接收码字序列本身所作的任何一种测度,只要同步和非同步状态能显示出明显差别,就可用于鉴别同步,一切同步技术根本原理。
- 扩频码同步捕获依据
- 伪随机码序列由于具有优良自相关特性,码序列同步时,相关函数取最大值;不同步时,相关函数取值较小或接近零。
- 同步捕获操作
- 接收机选择和调整本地参考码序列相位,使它与接收扩频码序列相位一致。此过程就是捕获接收码序列相位的过程,又称为扩频码序列初始同步。
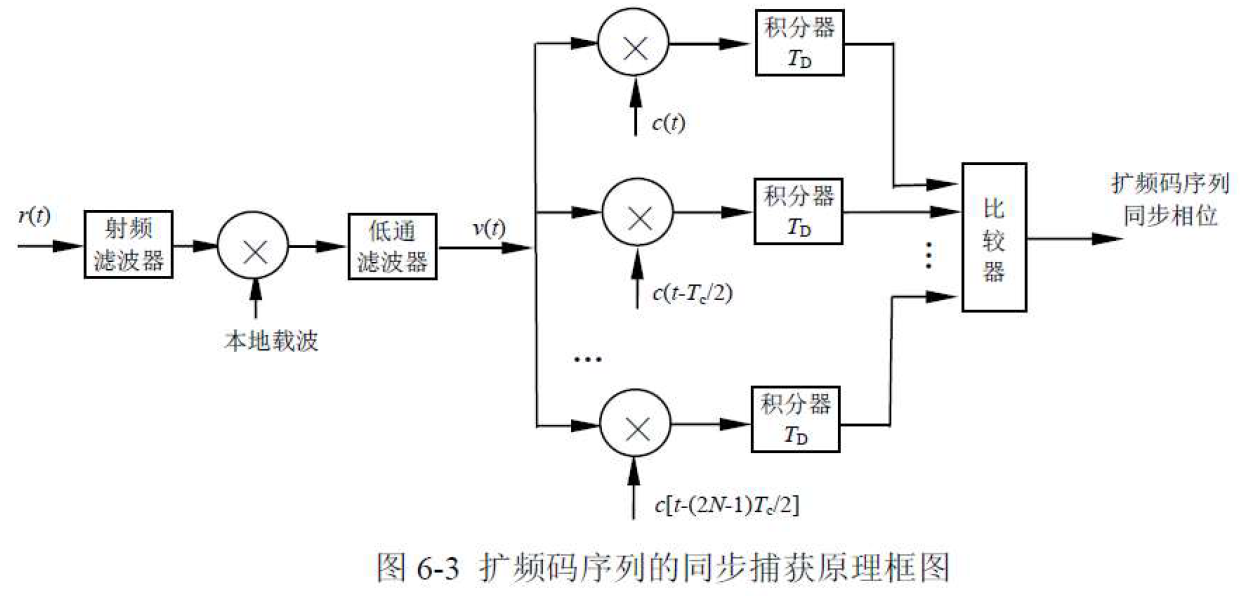
说明
- 采用2N个相关器。
- 使用同一本地参考码序列,相位各不相同,依次滞后半个码元。
- 积分器采用积分-清零方式。
- 2N个结果哪个最大,对应的码相位就是输入序列相位状态(接近),从而实现扩频码序列同步捕获。
扩频接收机接收信号:
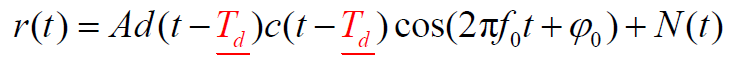
- 本地载波:
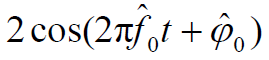
- 若载波已同步(频率和相位都同步),低通滤波器输出为:
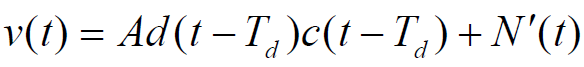
- 假设:积分时间
小于信息码元
,则 d(t) 可用一固定电平信号 (如+1) 代替
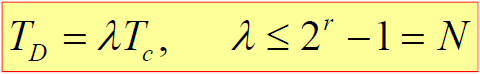
- 积分器输出:
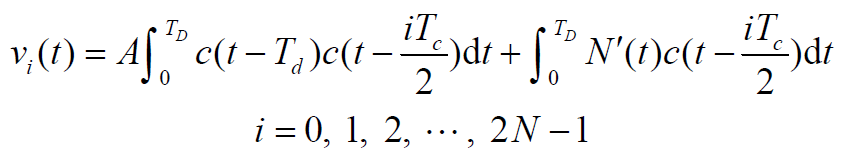
- 若相位延迟
满足:
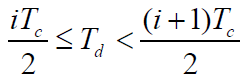
- 则 2N 个相关器中,第 i 个输出最大:
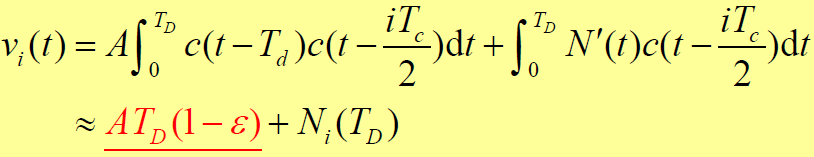
- 式中:
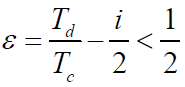 为归一化时间差
为归一化时间差
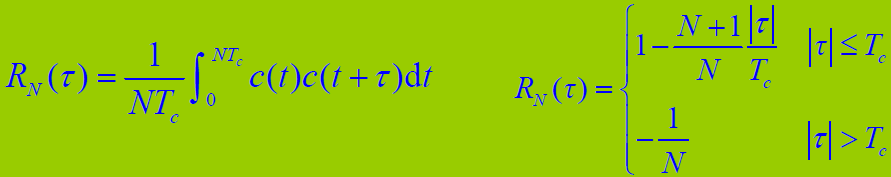
- 其它相关器输出:

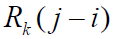 是扩频码中长为 λ 个码元的部分自相关,一般当 λ>r 时,有:
是扩频码中长为 λ 个码元的部分自相关,一般当 λ>r 时,有:
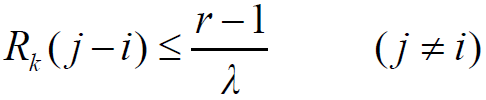
- 所以,在 λ>r 的情况下,下列不等式成立
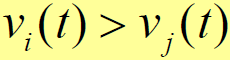
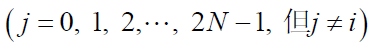
因此,若
最大,可知道
最接近接收扩频码序列的相位,实现了扩频码序列的同步捕获,
就是同步捕获电路给出的本地参考码的同步相位,即对
的粗略估计值。
扩频码同步捕获时间:
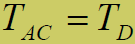
- 其中:

特点:
扩频码同步捕获问题是扩频通信中的一个核心问题。
- 理论上:
- 扩频码同步捕获原理就是计算并比较扩频码在 2N 个相位状态下的相关值。
- 工程上:
- 扩频码同步捕获包含两方面内容:
- (1)设备简单
- (2)时间短
- 同步捕获步骤:
- (1) 确定搜索扩频码的相位区域
- (2) 调整本地参考扩频码相位
- (3) 求解扩频码相关函数值
- (4) 对相关值进行判决
- (5)估计扩频码最可能的相位
同步捕获分类:
- 根据区域的搜索方法:
- 序列相位顺序搜索法,序列相位概率分布搜索法等;
- 根据改变本地参考码相位方法:
- 序列相位步进捕获法,序列滑动相关捕获法等;
- 根据同步捕获的判决方法:
- 单积分判决和多积分判决同步捕获等;
- 根据使用器件不同:
- 相关器同步捕获,匹配滤波器同步捕获等
- 匹配滤波器同步捕获又有:
- 声表面波器件(Surface Acoustic Wave,SAW)同步捕获
- 电荷耦合器件(Charge Coupled Device,CCD)同步捕获
- 根据区域的搜索方法:
不论如何分类,都是通过调整本地参考扩频码的相位,求解扩频码相关函数值
- 尽可能准确地估计出接收扩频码相位
-
6.2.1 搜索区域的确定
无码相位信息:
- 通常假设相位在2N个单元中服从均匀分布。
- 只能采用顺序搜索办法。
- 搜索可以从2N个单元位置中的任意一个开始,直到获得扩频码同步捕获为止。
- 已知码相位信息:
- 如果已有扩频码相位先验信息,则不宜采用顺序搜索。
- 例如:GPS接收机,在上一次接收卫星信息时,通过卫星的授时系统修正接收机时钟,使得接收机的时钟与卫星时钟基本保持一致;通过上一次扩频码同步信息就可以推断出本次接收信号中扩频码可能相位。
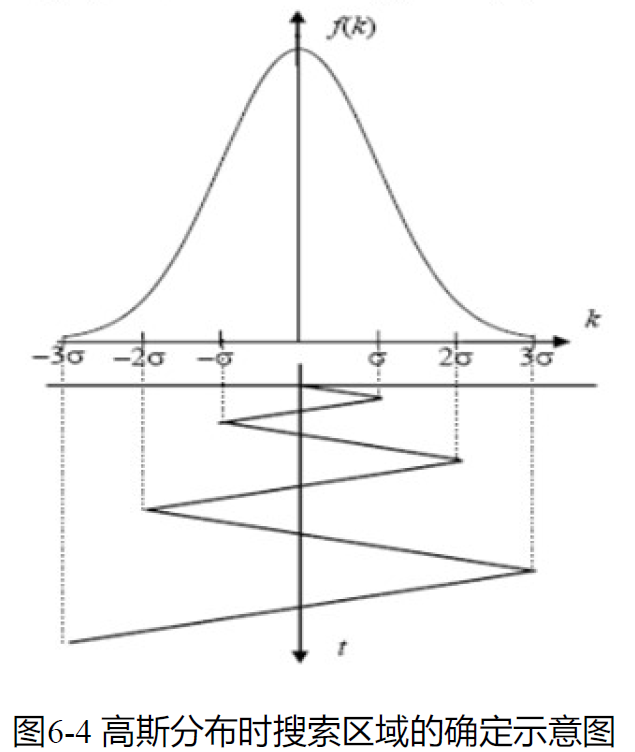
- 若已知扩频码相位所在位置先验概率P(k) ,首先应搜索那些最可能的扩频码相位单元,而后搜索次可能相位单元。
- 例如:假设扩频码相位服从高斯分布,较合理的搜索方法是先搜索以最可能的相位位置为中心的一个标准偏差范围内的单元。如没有搜到,扩大到两个标准偏差范围,依此类推。
6.2.2 序列相位搜索捕获法
- 工作原理:
- 扩频码捕获原理用2N个并联相关器结构来实现,设备量太大。
- 可以使用一个相关器来完成扩频码相位的搜索,称为扩频码序列相位搜索法。
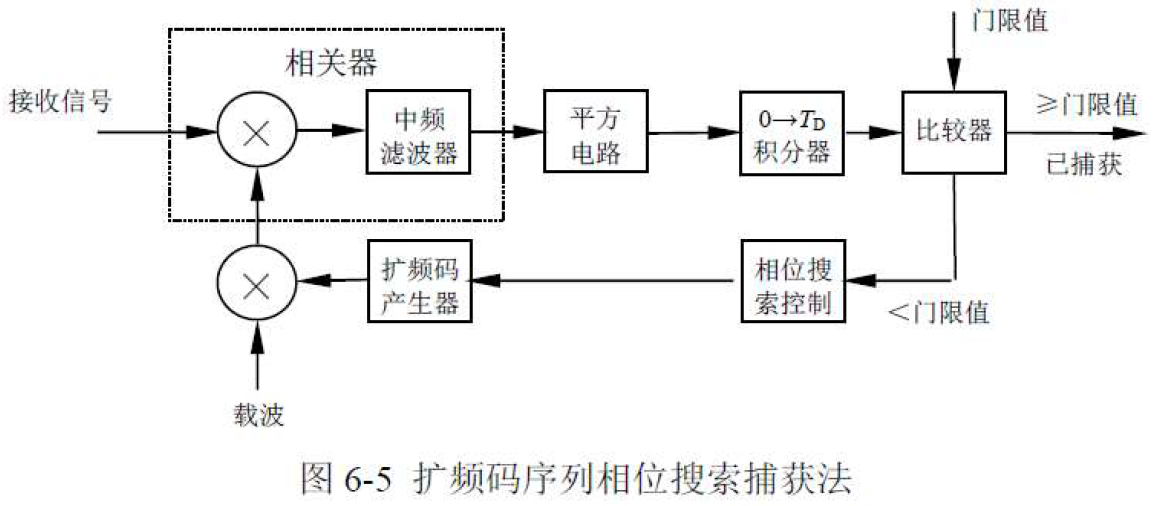
- 只使用一个相关器
- 积分时间为
- 本地参考扩频码相位状态变化量为
性能分析:
- (1)无漏检和虚警情况
- (2)有漏检和虚警情况
(1)无漏检和虚警情况
- 设扩频码序列长为N,码元宽度 Tc,周期 NTc
设检测概率为 Pd =1 ,虚警概率为 Pfa = 0 ,搜索相位改变增量为 Tc/2 ,则:
最大同步捕获时间:
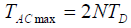
- 最小同步捕获时间:
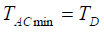
- 平均同步捕获时间(各相位等概出现)
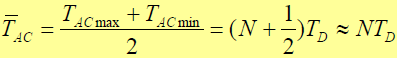
- 结论:序列相位搜索捕获法平均同步捕获时间,比使用 2N 个扩频码序列相关器捕获时间约大 N 倍。
- (2)有漏检和虚警情况
- 存在虚警情况:
- 研究虚警惩罚时间 (False Alarm Penalty Time)
- 假如某次积分处理出现虚警,则相位搜索控制电路不改变本地码相位,再作一次积分处理来证实是否发生虚警。
- 若此次积分处理不发生虚警,即证实前次积分处理是一次虚警,则下次积分处理将使相位改变Tc/2 ,接着重新开始搜索。
- 两次积分处理,本地参考码相位仅改变了Tc/2 ,出现虚警后的这次积分处理仅证实虚警发生,对相位改变毫无贡献,将此时间称为虚警惩罚时间,表示由于虚警浪费的时间。
- 若证实虚警发生的这次积分处理又发生了虚警,即接连出现两次虚警。由于虚警后本地参考码相位不发生变化,所以连续出现两次虚警惩罚时间为2TD。同理,连续出现三次虚警的惩罚时间为3TD ,…。则完成一次成功捕获的虚警惩罚时间为:
- 存在虚警情况:
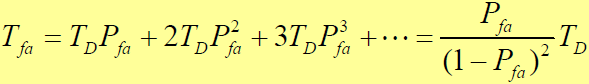
- 考虑虚警惩罚时间后的平均同步捕获时间:
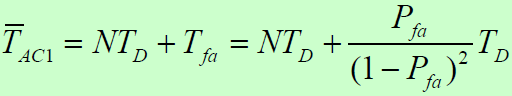
- 存在漏检情况:
- 若门限比较器的正确检测概率 Pd<1 ,则有 (1-Pd) 的概率, 在已经搜索到同步相位时,门限比较器不能给出完成捕获的输出信号(漏检),而要再做一次紧随其后的、相差NTc (正好一个周期)的相位搜索。
- 作一次这种搜索需要的平均同步捕获时间为:(可理解为漏检惩罚时间)。
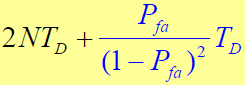
- (最后一项是虚警惩罚时间)- 扩频码序列已经捕获,但出现了概率为(1-Pd) 的不正确检测,则又要搜索NTc 个相位才能再一次捕获,随后还可能有 (1-Pd) 的概率出现一次、二次…等的不正确检测输出。- 不论出现几次不正确的检测,都要再搜索NTc个相位。因此,完成这种相位的搜索,最终花费平均时间(漏检惩罚时间)为:
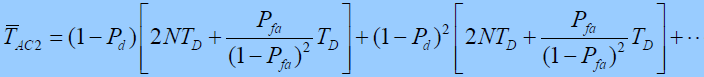
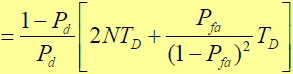
- 综合考虑情况:
- 相位搜索捕获法的平均同步捕获时间为:
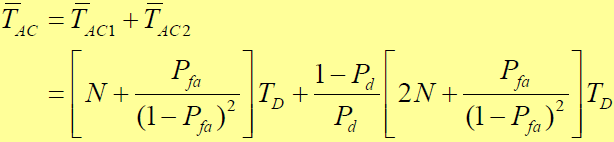
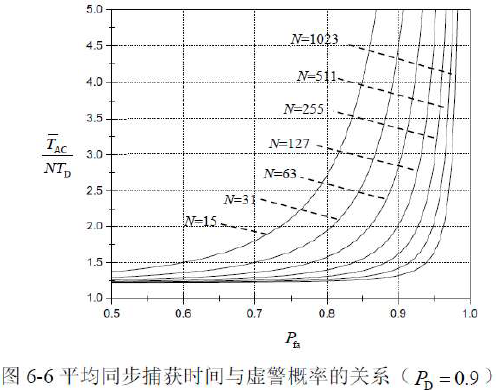
- 分析:- 扩频码序列相位搜索捕获法平均同步捕获时间至少是相关积分时间的N倍- 当码周期N较小时,虚警对平均捕获时间的影响比较显著- 当N较大时,比如N >100 ,只有在  时,虚警对平均捕获时间的影响才显著地表现出来。通常N取值都较大,而虚警概率也不可能接近1,故工程可认为虚警概率为零
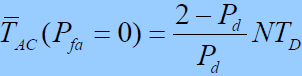
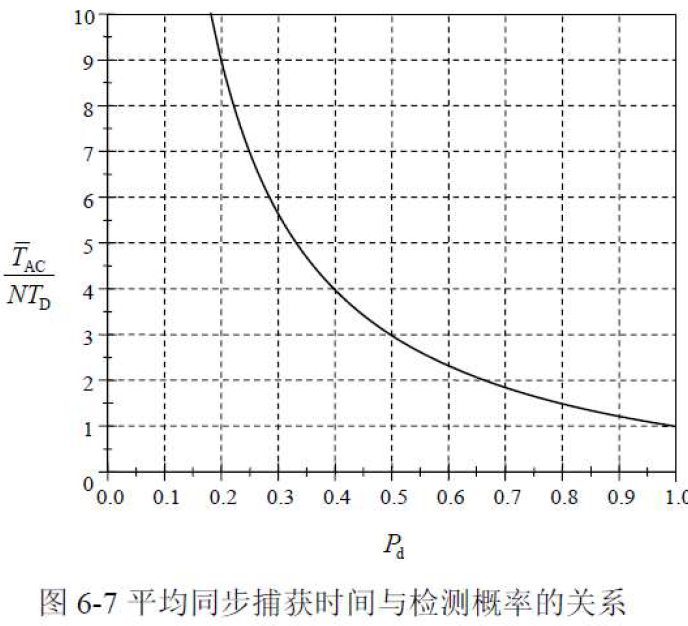
- 随着检测概率的降低,平均同步捕获时间将迅速增大。- 由于Pd <1,所以可得:

- 平均捕获时间随着检测概率的降低成反比例上升。
总结:扩频码序列相位搜索捕获法电路设备量少,但平均捕获时间随扩频码长度的增加而增大,要实现快速捕获很困难,特别是在扩频码长度比较大的情况下。
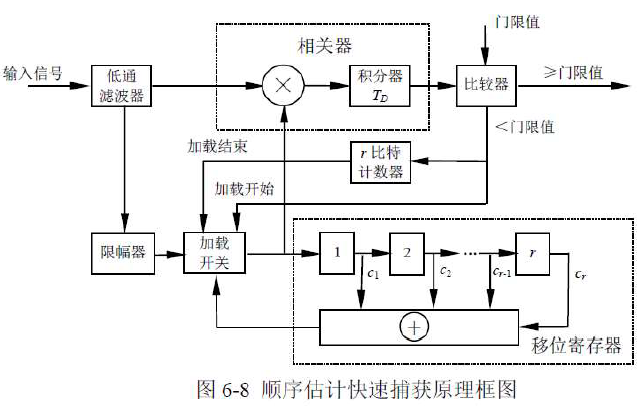
6.2.3 顺序估计快速捕获法
现象:
- 由线性反馈移位寄存器产生的伪随机序列,每一个时刻移位寄存器所处状态都可在所产生的伪随机序列中找到。
思想:
- 如能由接收信号准确估计出接收信号在某时刻移位寄存器应有的状态,并从这一状态开始产生伪随机序列,则此伪随机序列将与接收序列相匹配。
基于上述想法产生一种适用于基带信号的顺序估计快速捕获法
(Rapid Acquisition by Sequential Estimation,RASE)
假设:输入信号是取值±1的二元序列与加性高斯白噪声
- 平均同步捕获时间研究:
- 假设:准确估计一个接收符号概率是p,p是输入信噪比函数。
- 对 r 级都准确加载的概率就是
,移位寄存器没有准确加载的概率是(
) 。
- 在第 k 次获得准确加载的概率为:
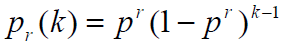
- 则实现准确加载的平均次数为:
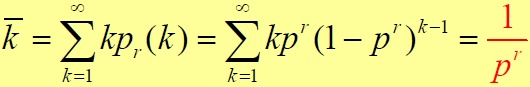
- 移位寄存器每次加载需要
秒,积分处理时间
- 在正确检测概率 Pd=1 时,RASE平均同步捕获时间:
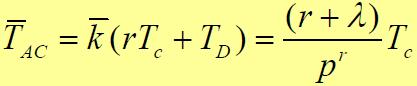
- 低信噪情况:
- 低信噪比情况,p近似为0.5;平均同步捕获时间为:
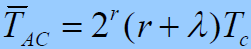
- 高信噪情况:
- 高输入信噪比情况,p≈1。平均同步捕获时间为:
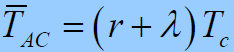
讨论:
- (1) 在低输入信噪比情况下, RASE平均同步捕获时间要比序列相关捕获法(
)长
- (2) 在高输入信噪比情况下, RASE平均同步捕获时间可以远远低于序列相关捕获法同步捕获时间
- (1) 在低输入信噪比情况下, RASE平均同步捕获时间要比序列相关捕获法(
-
6.3 匹配滤波器同步捕获法
6.3.1 匹配滤波器原理
任意滤波器输出都是输入信号和滤波器冲激响应的时域卷积积分,即
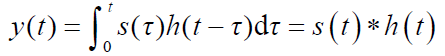
- 当信号被高斯白噪声污染后,匹配滤波器使其输出信噪比最大,理论分析表明,在
的时间间隔内,匹配滤波器的冲激响应是输入信号的时间反转,即
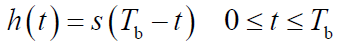
- 匹配滤波器传输函数:
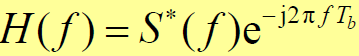
- 输入信号为BPSK调制:
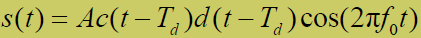
- 在一个信息码元持续时间 Tb 内,d(t) 取值为常数 d(t)=1
- 在无噪声情况下,扩频码 N 码元 BPSK 波形可写为:
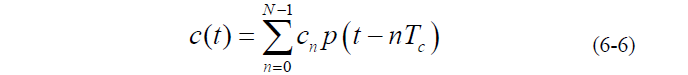
- 式中,cn =±1是扩频序列,p(t) 扩频码一个码元内的基本波形。
- 对式(6-6)傅立叶变换:
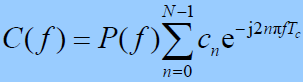
- P(f) 是基本脉冲信号 p(t) 的傅里叶变换
- 当基本脉冲波形为矩形方波时,p(t) 即闸门函数
,因此
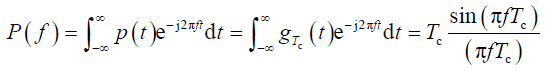
- 显然,P(f) 是实函数,所以
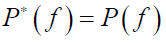
- 从而,得 s(t) 的傅立叶变换为:
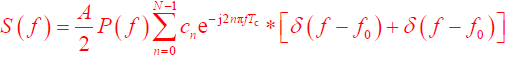
- 利用式
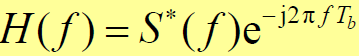 和上式,可得匹配滤波器的传输函数(注意:
和上式,可得匹配滤波器的传输函数(注意:)
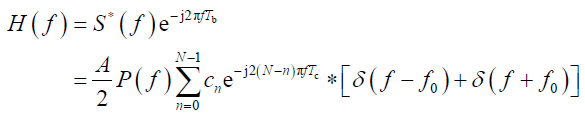
- 可以看出,与信号 s(t) 相匹配的滤波器,是一中心频率位于载波频率
处的带通滤波器,冲激响应为:
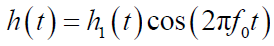
- 其中
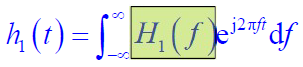
- 而
为匹配滤波器的低通等效传输函数:
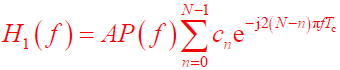
- 由此可知,与信号 s(t) 相匹配的滤波器,其传输函数应为脉冲波形 p(t) 的频谱移相
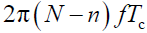 与扩频码元
与扩频码元 乘积的累加
- 而频域的相移为时域的延时,因此可用延迟线来实现信号 s(t) 的匹配滤波器
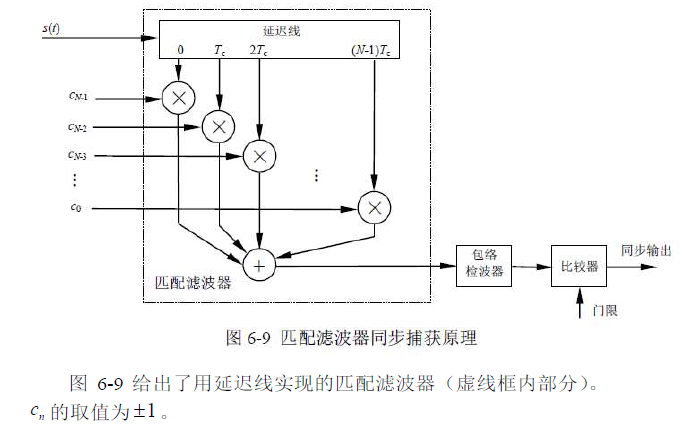
- 载波为
的BPSK 信号在延迟线内被延迟了
 延迟后的信号分别与
延迟后的信号分别与相乘,只有在 N 个乘法器输出信号的相位完全相同时,加法器才有最大的输出。
- 只有当进入延迟线的信号 s(t) 中的扩频码序列与本地参考扩频码序列
完全相等时,N 个乘法器输出信号的相位才能完全相同
当包络检波器输出最大时,此时输入信号 s(t) 中的扩频码序列的相位与本地参考扩频码序列
的相位完全相同,完成了扩频码的同步捕获。通过包络检波器和门限判决器,将同步时的最大值取出,作为同步跟踪的启动信号。
实际工程中,有时对整个周期的扩频码匹配难以实现,只能对周期内的一部分或大部分码元实现匹配,这也是可行的。
- 假设在
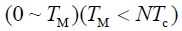 间隔内,与 s(t) 匹配的滤波器的冲激响应为:
间隔内,与 s(t) 匹配的滤波器的冲激响应为:
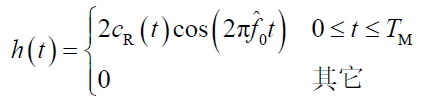
- 式中,
是扩频码 c(t) 的长为
的一段逆时间序列。
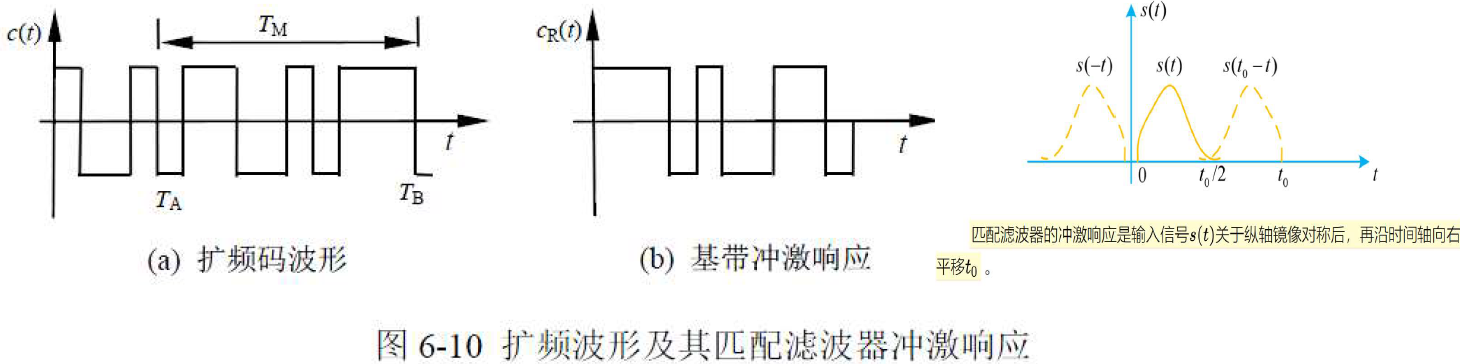
- 匹配滤波器输出(忽略高次谐波
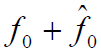 的成分):
的成分):
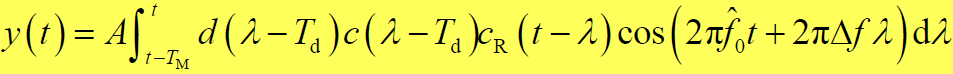
- 式中
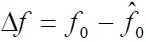 是包括多普勒频移在内的接收信号的频率偏移。在
是包括多普勒频移在内的接收信号的频率偏移。在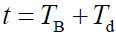 时刻,
时刻, 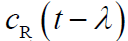 和
和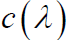 的一段是匹配的,此时乘积
的一段是匹配的,此时乘积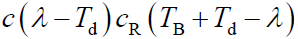 在积分区间内等于1。
在积分区间内等于1。 - 假设:数据信号相对于扩频码序列是缓慢变化的(即处理增益很高), 在积分期间(
)内可以看成是等于 ±1 的常数 d,则有:
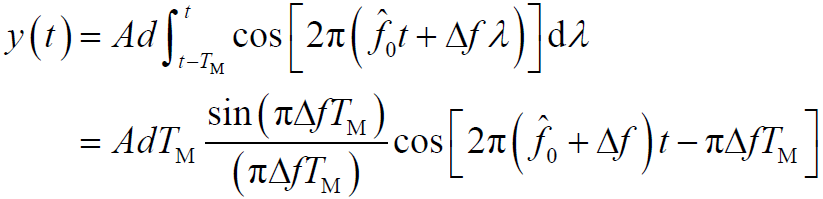
- y(t)的极大值为:
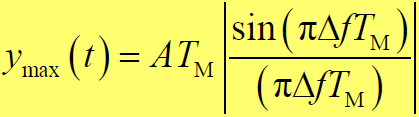
- 设法消除接收信号频率偏移Δf ,可以使匹配滤波器输出最大。
- 设若接收机的载波已经同步,即
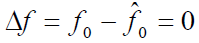 ,则有:
,则有:
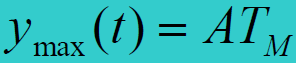
特点:
滑动相关捕获法 (Sliding Correlator Acquisition)
- 基本思想:
- 使本地码时钟与接收码时钟频率有一定偏差,通过改变本地扩频码产生器时钟频率来达到改变码序列相位,两个序列从相位上看好象在相对滑动。滑动到两个码序列相位一致时停止滑动。
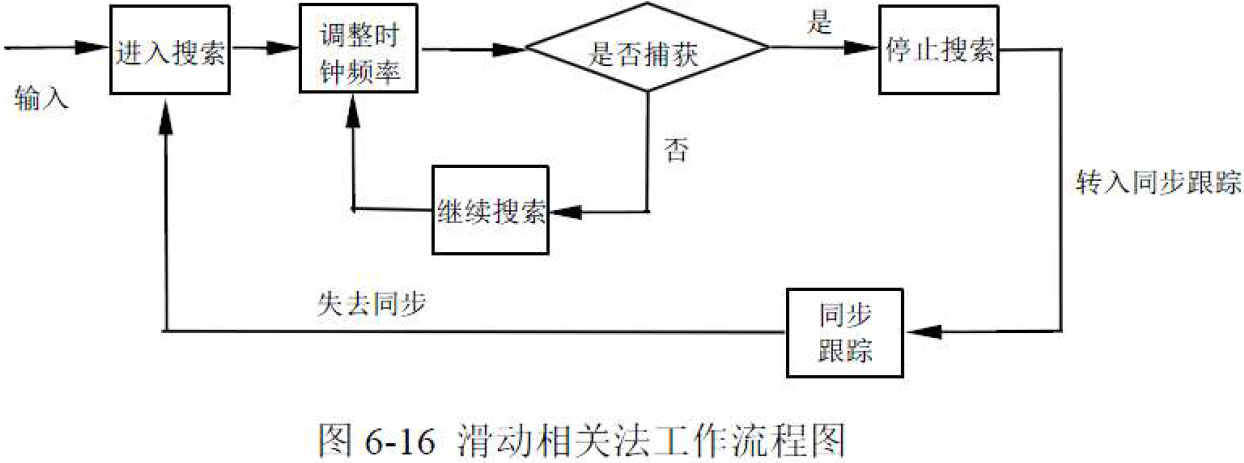
滑动相关法特点:
- 结构简单,搜索时间长
- 当扩频序列间失配很大时,搜索过程可能很长。
- 在某些场合(失配达上万比特),若仅用滑动相关器将花费几十分钟,甚至几个小时
- 工程上首选方案
- 也可与其他方法结合,先使两个扩频码序列的相位接近到一定程度,再用滑动相关法实现捕获
- 结构简单,搜索时间长
滑动相关法分类:
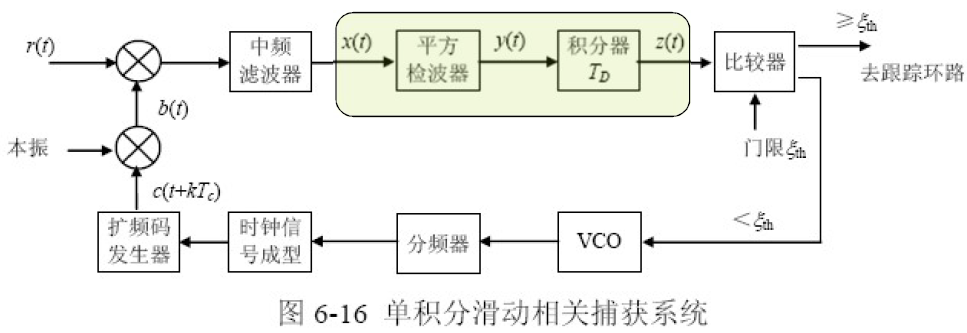
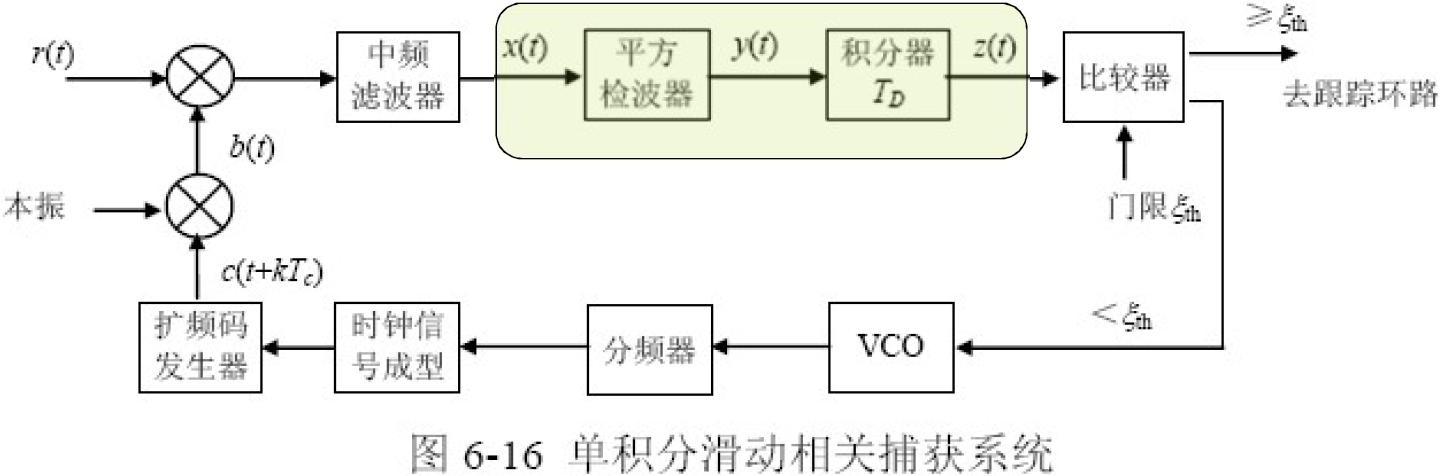
工作原理:
- 接收信号相关处理后,变为中频窄带信号,经平方检波后送到积分清除积分器。
- 若低于设定门限值,则改变时钟频率,改变本地参考序列相位状态。
- 若输出大于门限,则完成序列相位捕获,不再改变时钟电路,同时输出信号给同步跟踪电路,进入扩频序列同步跟踪。
- 特点:
- 滑动相关过程中,由于没有载波同步,不可能进行相干检测,因而采用包络检波进行非相干检测
时钟电路:
- 由压控振荡器(VCO)、分频器和时钟信号成型等组成。门限比较器输出控制VCO输出信号的频率,结果相当于本地参考序列相位作
滑动
- 若参考序列与接收序列相位差 ΔTc ,每次积分后参考序列相位滑动半个码元,则总共要作 2Δ 次相位滑动,此时同步捕获时间为 2ΔTD 。
- 注意:当扩频序列长度为N时,经2N次相位滑动则将遍历码序列整个周期的各个相位状态。
- 由压控振荡器(VCO)、分频器和时钟信号成型等组成。门限比较器输出控制VCO输出信号的频率,结果相当于本地参考序列相位作
【1】若门限比较器检测概率 Pd =1,虚警概率
,则:
- 最小同步捕获时间:
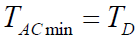
- 最大同步捕获时间:
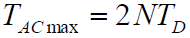
- 平均同步捕获时间:

- 【2】若Pd ≠1 (0≤Pd<1),Pfa≠0( 0<Pfa≤1):
- 数学模型:捕获过程可建模为马尔可夫链模型,通过生成函数信号流图方法得到。
- 平均同步捕获时间:
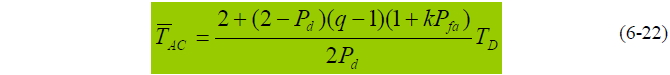
- 式中:- k 发生虚警时证实虚警发生所需的判决次数-  证实发生虚警所需时间(虚警惩罚时间)- q 搜索单元数,在每次滑动半个码元情况时,有 q=2N- 由于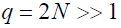 ,平均同步捕获时间近似为:
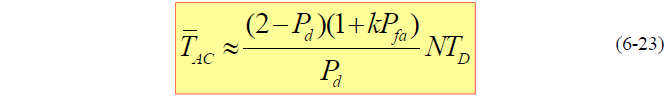
- 捕获时间方差:
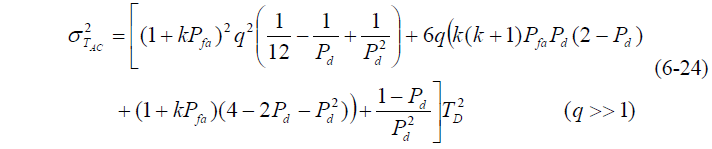
- 当 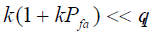 则:
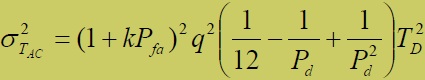
- 注意:由于k是一个随机变量,故式(6-22)与(6-24)结果也是 RVs,很难给出准确值。
检测概率
、虚警概率
、驻留时间
的关系:
- 【目标】:平均捕获时间及方差是检测概率
,虚警概率
和驻留时间
的函数。它们之间的关系如何?
- 【假设】:捕获时只有一个检测状态(cell)表示信号被捕获成功。
- (实际应用中,由于PN码相关峰值两侧±1个码片内都有相关值,因此若按1/2码片增量进行捕获,将会在峰值附近产生多个信号捕获的状态。)
- 【假设】:
- ① 接收信号由扩频序列调制的BPSK信号和窄带高斯白噪声信号组成;
- ② 积分时间内数据信号保持不变;为简化推导,假设无数据调制;
- ③ 假设系统已经处于同步状态,
- 【目标】:平均捕获时间及方差是检测概率
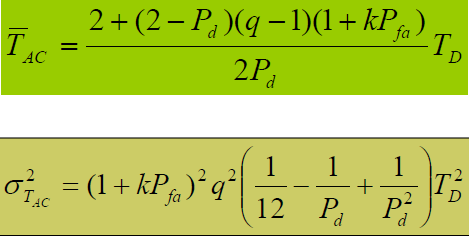
- 相关检测后平方检波器输入信号为:
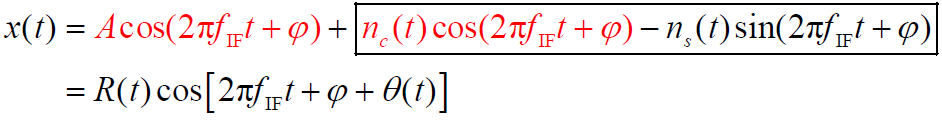
- 其中:
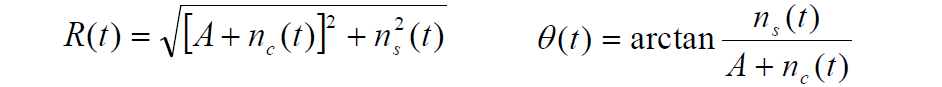
和
为窄带高斯白噪声,方差为
,
为高斯白噪声功率谱密度,B为中频滤波器带宽。
平方检测器输出:(忽略二倍频载波分量)
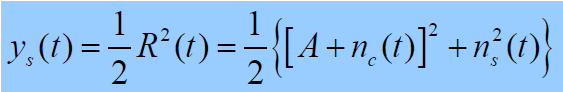
- 注意:
是二自由度非中心 χ2 分布,其 pdf 为:
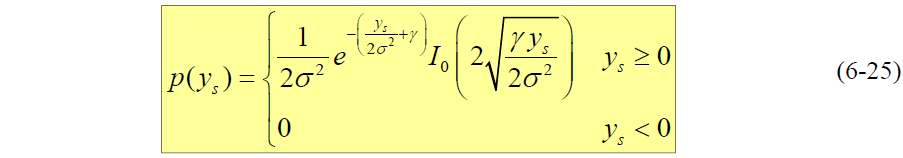
- 式中:
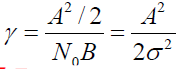 为信噪比;
为信噪比;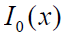 为零阶修正贝塞尔函数
为零阶修正贝塞尔函数 - 当无信号时,即A=0,则上式变为:
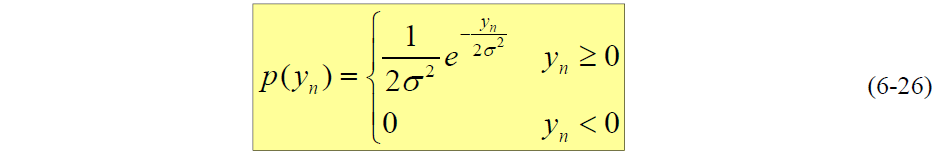
- 若信号 y(t) 以 τ=1/B 的间隔抽样 ( B 为中频滤波器等效噪声带宽),抽样值近似为相互独立。则积分器输出可近似为抽样值之和,即:
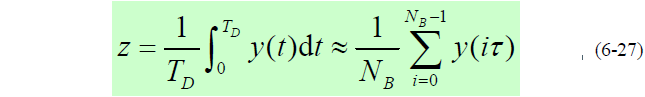
式中:
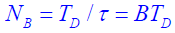 为
为时间间隔内的样值个数
(1)信号存在时,检测量 z 的概率密度函数pdf为:
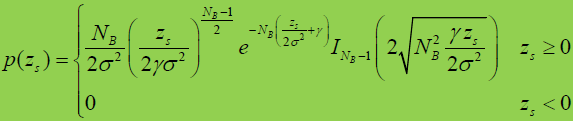
- (2)信号不存在时,检测量 z 的概率密度函数pdf为:
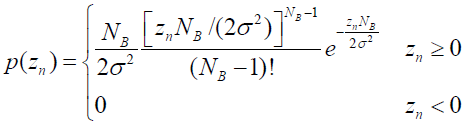
- 虚警概率:当信号不存在时,检测量 z 超过门限值
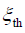 的概率
的概率
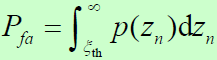
- 检测概率:当信号存在时,检测量z超过门限值
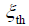 的概率
的概率
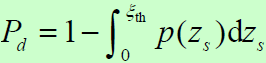
- 整理得:
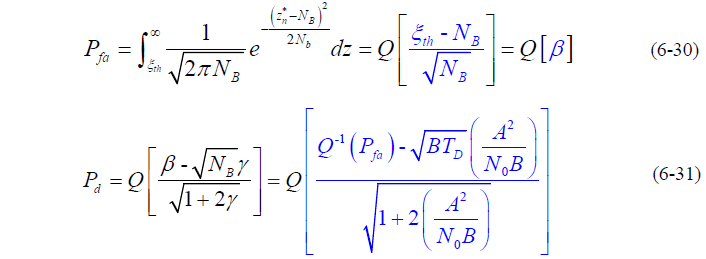
- 结论:
面临的问题:如何进一步缩短捕获时间?
- 单积分滑动相关捕获电路简单,但当扩频序列很长时,同步捕获时间很大
- 从平均的观点看,每次同步捕获从开始到完成过程中必定要经历许多非同步状态,因为同步相位只有一个,其余N-1个都是非同步相位
- 减小积分时间,当然能快速抛弃(判决出)非同步相位。同时,虚警概率将增大,导致花费更多时间来消除虚警(增加虚警惩罚时间)才能使电路进入同步状态。
- 单纯减小积分时间不是解决问题的办法。
解决思路:
- 采用多积分检测:由多个积分电路组成,彼此积分时间不同。
- 捕获初,先用积分时间最短的积分器进行积分判决,可快速抛弃非同步状态(同时引起很高的虚警概率)。
- 若检测器输出大于门限值,判决为同步(含虚警),再用积分时间更长的积分器检测(进一步去除虚警),直至所有检测器输出都大于对应的门限值时,才判为同步。
- 通过快速去除非同步相位,降低系统平均同步捕获时间。
最常采用双积分检测,将单积分滑动相关同步捕获系统改为双积分滑动相关同步捕获系统。
根据积分器相对位置不同,分为:
- 串行双积分滑动相关捕获系统
- 并行双积分滑动相关捕获系统
串行双积分滑动相关捕获系统
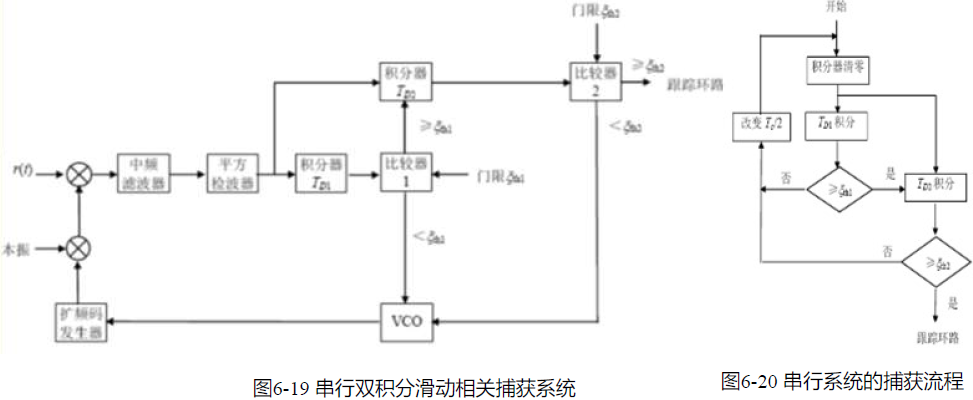
- 积分时间:
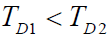
- 第一个积分器仅提供序列相位捕获的粗略估值,第二个积分器提供本地参考序列是否进入同步跟踪的更准确估值。(提供更高的检测概率、更低的虚警概率。)
- 平均同步捕获时间:
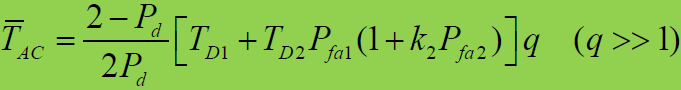
- 方差:
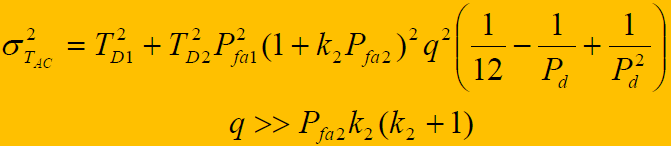
式中:
两个积分检测器都正确检测的联合概率
第二积分检测器虚警代价,即第二积分检测器消除一次虚警进行
积分次数
- q 消除本地参考序列相位与接收序列相位之差所需相位滑动次数
- 若
即第一积分检测器不起作用,则串行双积分捕获系统退化为单积分滑动相关捕获系统。
并行双积分滑动相关捕获系统
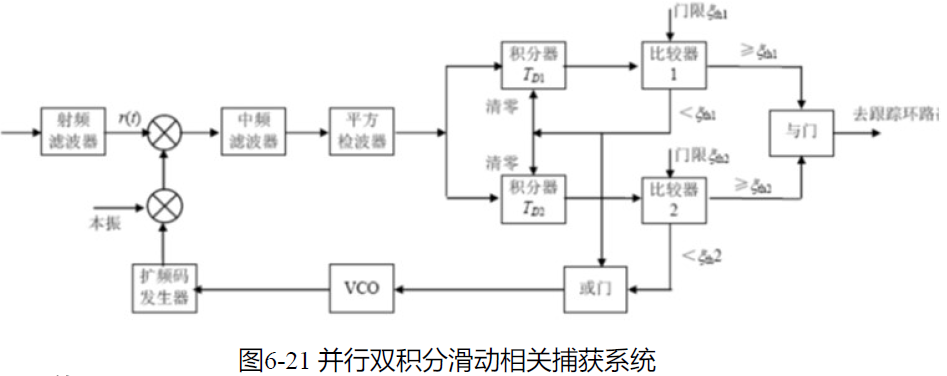
工作原理:
- (1)积分时间满足
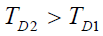 ,同时并行积分
,同时并行积分 - (2)捕获开始,积分器1进行积分并判决,若小于门限值,则对两个积分器同时清零,并开始下一个相位检测
- (3)若大于门限,则积分器2继续积分判决,直到两个积分器都大于门限值时,表明扩频序列已同步,完成同步捕获
- (1)积分时间满足
等效模型:
- 等效为一个积分检测器,其输出依次在 TD1 和 TD2 时刻采样并判决。
- 任何一次判决小于门限,则积分器清零,进行下一个相位检测。
- 如果在时刻 TD1 的判决大于门限,则可以等到 TD2 时刻作下一次判决。
- TD2 时刻判决大于门限,则捕获成功。
平均同步捕获时间:
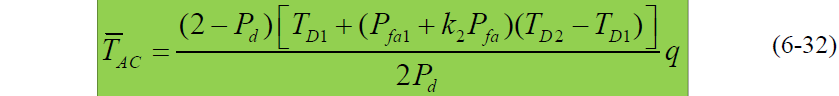
- 方差:
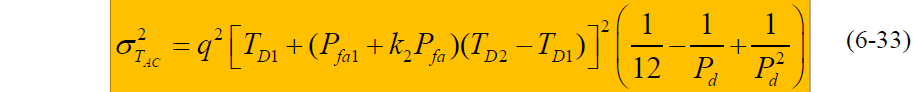
- 式中:
- Pd=Pd1Pd2 为联合概率
- Pfa=Pfa1Pfa2 为联合虚警概率
- q 是最大相位滑动次数,一般 q=2N
- k2 是第二积分检测器的虚警代价,即第二积分检测器消除一次虚警进行TD2积分的次数,虚警惩罚时间为 k2(TD2-TD1)
- 滑动相关捕获系统性能比较
- 单积分滑动:
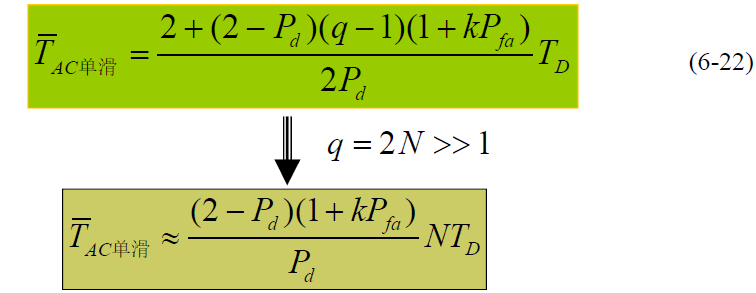
- 并行双积分:
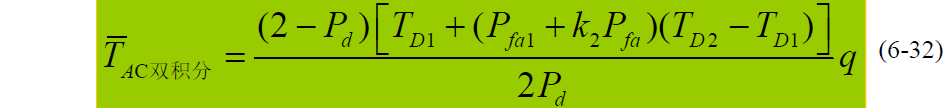
- 在虚警惩罚时间相等情况下,即
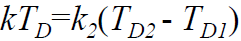 ,只要再满足
,只要再满足
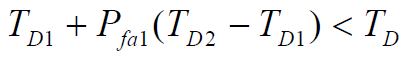
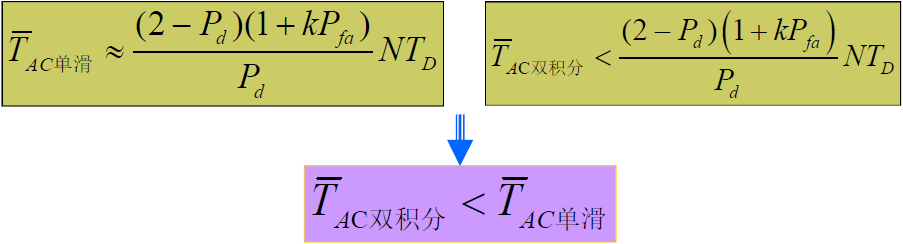
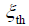 有关。
有关。
