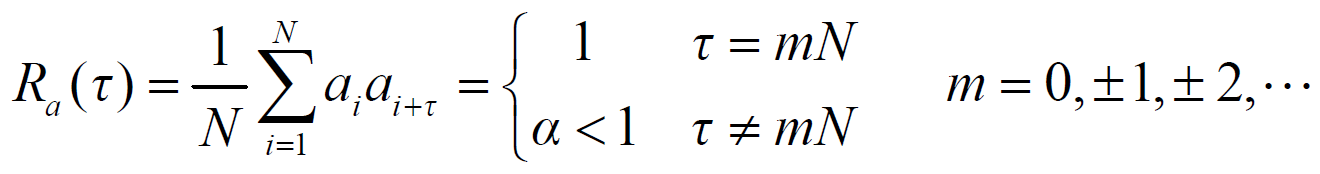3.1 有限域理论简介
（1）运算的自封性：
- 设F是一个非空集合，若F中的任意两个元素a、b的和与积仍是F中的元素
- 则称F对于加法运算与乘法运算是自封的或封闭的
（2）域：
- 若F对于规定的加法与乘法运算是自封的，且以下运算规则成立：对任意
有：
- 若F对于规定的加法与乘法运算是自封的，且以下运算规则成立：对任意
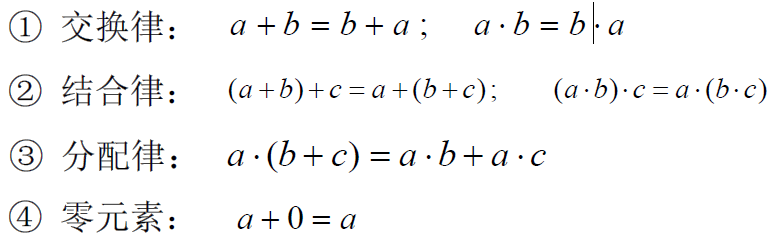
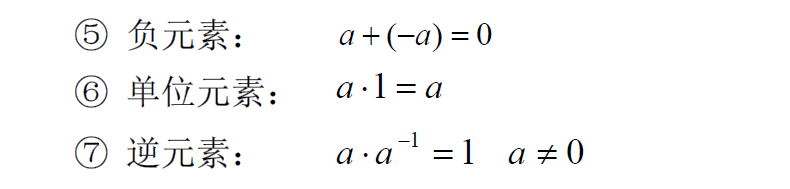
- 则F对于所规定的加法运算与乘法运算是一个域
- 阶数：域F中元素的个数
- 无限域：F的元素个数为无限个
- 有限域或伽罗瓦(Galois)域：F元素个数有限
- n阶有限域：F中有n个元素
- 一般来说，对整数集
- 若p为素数，对于模p的加法运算与乘法运算来说， p是一个有限域
- （3）域上多项式：
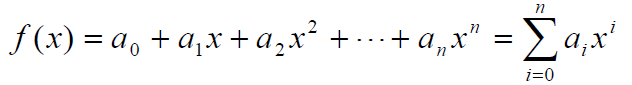
- 称 f(x) 为域F上的n次多项式，记作
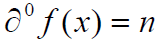
- 其中：
是域F的元素， 
称为 f(x) 的首项，
叫做的首项系数 - 记域 F上所有多项式组成的集合为 F(x)
- （4）域上多项式运算：
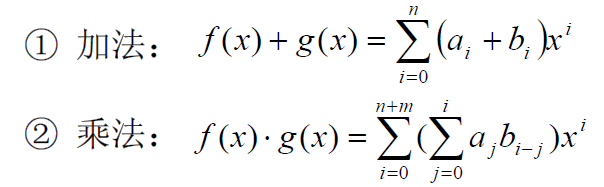
- 例子
（5）群
- 由上知道：在一个域中可以进行加法与乘法两种运算
- 定义：如果在一个元素集合G中只能进行加法或乘法中的一种运算，就把G叫做加法交换群或乘法交换群
- 无限交换群：若G的阶(即元素个数)是无限
- 有限交换群：若G的阶有限
- 域F对加法是一个交换群，而F中所有非零元素组成的集合F*，对于乘法来说也是交换群
注意：“域”和“群”的区别
无限阶元素：
- 设 a 是乘法交换群 G 中的任意一个元素，若对于任意正整数n都有
，把 a 叫做无限阶元素
- 设 a 是乘法交换群 G 中的任意一个元素，若对于任意正整数n都有
- 有限阶元素：
- 如果有正整数n使
，就把a叫做有限阶元素，而使
的最小正整数n称为a的阶 - 若 a 是一个n阶元素，则
- 如果有正整数n使
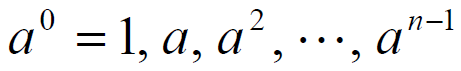
- 是G中n个不同元素- 由此得知：有限交换群中所有元素都是有限阶的
- n阶循环群:
- 设G是一个n阶乘法交换群。若G中有一个n阶元素，G中n个元素都可以表示成a的幂，即
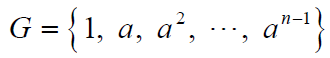
- 则此时G就是一个n阶循环群，而a叫做G的一个生成元- 可以证明：- 任一有限域F中所有非零元素组成的有限交换乘法群F*都是循环群- F*中一定有生成元存在，而有限域的交换群中的生成元称为该有限域的本原元- 若a是有限域F的一个本原元，则a一定是一个n阶元素，并且F的n个非零元素都可以表示成a的幂- 本原元另一定义：- 若有限域F中存在一非零元素a，F中的所有非零元素都可用a的幂来表示，则称元素a为有限域F的本原元- 可以证明：- 有限域中一定有本原元存在- 本原元个数：- 有限域理论证明：阶有限域中有个本原元- 其中： 是欧拉(Euler)函数，等于所有小于N的正整数中，与N互素的数的个数
3.2 伪随机编码基本概念
- Shannon信息论：
在高斯白噪声情况下，平均功率受限信道中，实现有效和可靠通信的最佳信号是具有白噪声统计特性的信号
白噪声是随机过程，正态分布，功率谱均匀分布
- 优点：优良相关特性，自相关函数类似于δ函数
- 缺点：无法进行放大、调制、检测、同步等操作
伪随机码（Pseudo Random Code，Pseudo Noise Code，PN码，伪噪声码/序列）就是一种人为构造的编码，用来逼近白噪声
- 工程中只能用类似于带限白噪声统计特性的伪随机码信号来逼近
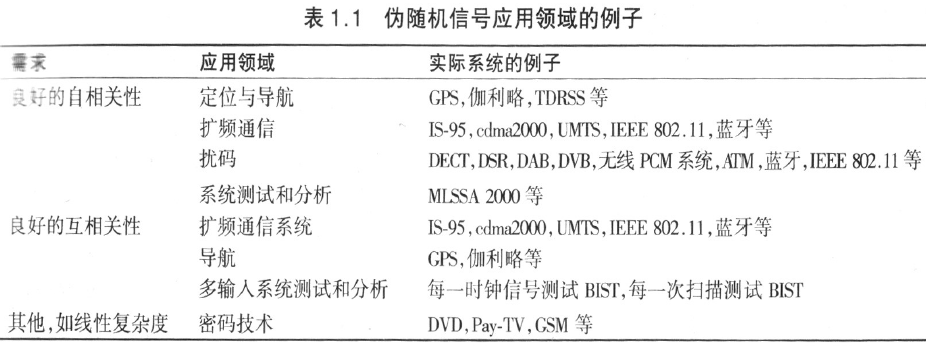
- 伪随机序列具有广泛应用：
- 扩频通信、测距、遥测、遥控和多址系统；
- 导航系统；
- 保密编码和抗干扰系统；
- 自动控制系统；－ 系统辨识
- 测量系统； － 噪声源
- 数字通信系统；－ 同步
- 期望伪随机信号具有下列特点:
- 伪随机码的特点：
- 工程上，常用二元域内的0与1元素的序列来表示伪随机码，特点如下：
- 游程：连续出现r个比特的同种元素叫做长度为r比特元素的一个游程（run）
- 互相关函数：
- 设
与
是周期为N 的两个码序列，即
- 则互相关函数定义为：
- 设
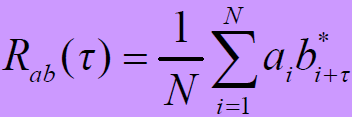
- 正交：若
，则
与
正交 - 也可表示为：
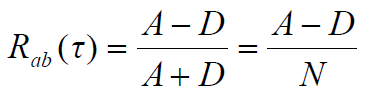
- 其中：A是对应码元相同的数目(同为元素1或同为元素0的数目)，D是对应码元不相同的数目
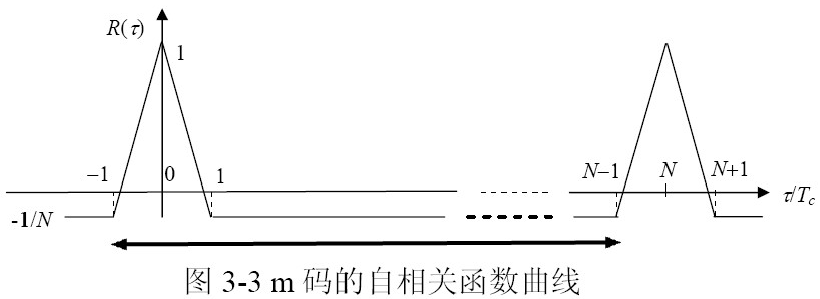
- 自相关函数
- 设
与
是周期为N的两个码序列，则自相关函数为：
- 设
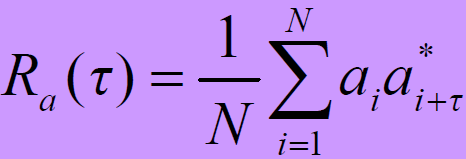
- 也可表示为：
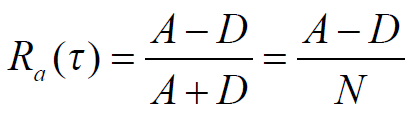
- 伪随机码定义
- 狭义伪随机序列
- 凡码长为N的周期序列
自相关函数具有
- 凡码长为N的周期序列
- 狭义伪随机序列
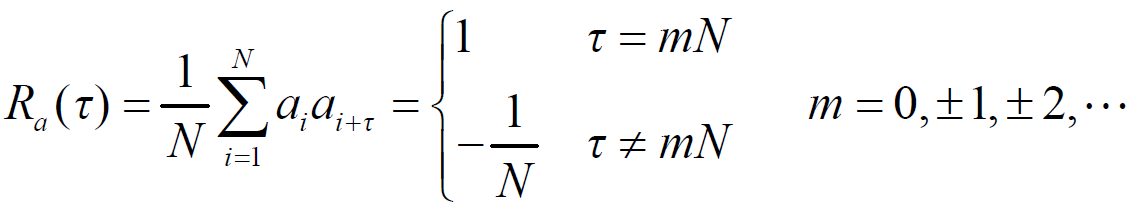
- 广义伪随机序列
- 凡自相关函数具有
3.3 伪随机编码的分类及构造原理
3.3.1 双值自相关序列定义
- 若码长为 N 的周期序列
自相关函数满足
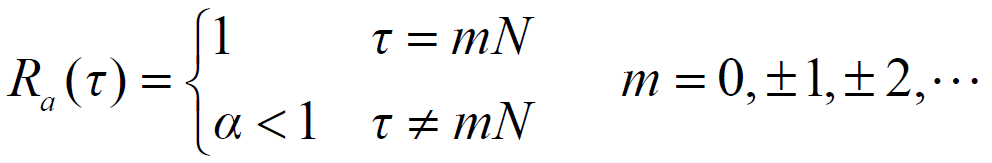
- 则称此序列为双值自相关序列
- 注意：双值自相关序列是狭义伪随机序列和第一类广义伪随机序列的总称
- 常见的双值自相关序列都是狭义伪随机序列，有：
- m序列
- 平方剩余序列（L序列）
- 双素数序列（TP序列）
- 霍尔（Hall）序列（H序列）
3.3.2 双值自相关序列的产生
- 双值自相关序列可以用构造差集的方法产生
- 差集
- 设有一个模 v 的整数集 V
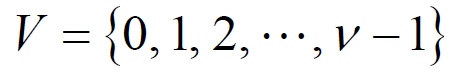
- 存在一个含有 k 个元素的子集 D，即
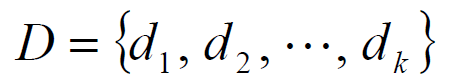
- 并且
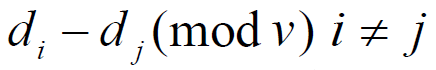恰好遍取 1，2，…，ν-1 各 λ 次，则把整数集 V 的子集 D，称为差集 - 表示：用ν，k和λ来表示一个差集，记为 （v，k，λ）
- 例子
- 注意：在给定 （v，k，λ）的条件下，差集不止一个
3.3.3 双值自相关序列构造方法
- 对于给定的差集 （v，k，λ），则有：
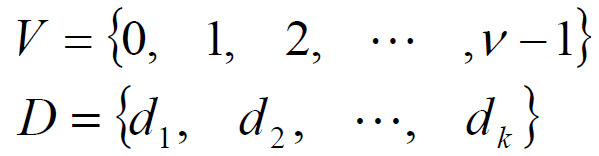
- 令序列
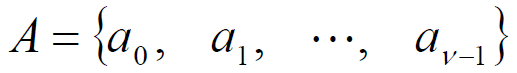为一长度等于 ν 的码，且
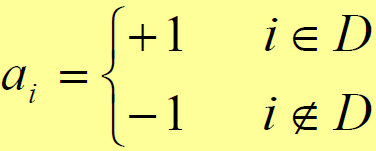
- 则
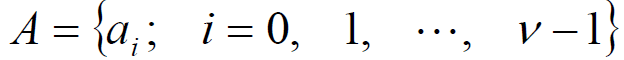就是一个周期为ν的双值自相关序列 - 可以证明：双值自相关序列的自相关函数：
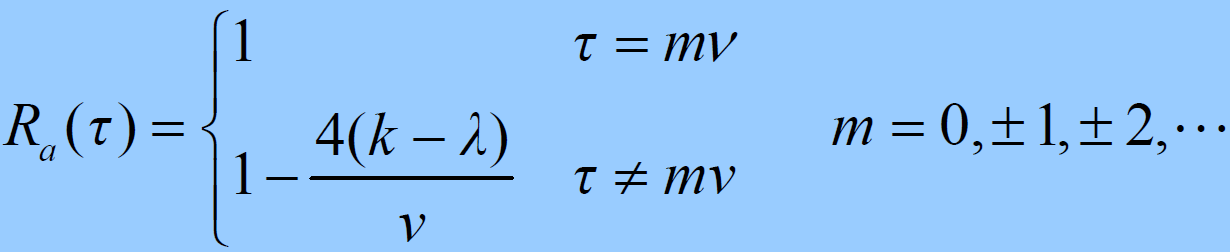
- 例子
- 注意：只要给出差集，可很容易写出对应的伪随机码序列
- 但是在给定n，k，v的条件下，要找出差集D并非易事
- 由差集D构成的双值自相关序列，可能是第一类广义的伪随机码序列，也可能是狭义的伪随机码序列。
- 只有当：
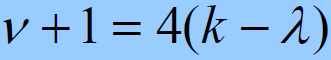
成立时，所得的才是狭义伪随机码序列；否则是第一类广义伪随机码序列。
常见的双值自相关序列都是狭义伪随机序列，它们有
- m序列
- 平方剩余序列（L序列）
- 双素数序列（TP序列）
- 霍尔（Hall）序列（H序列）
素数：
- 恰有1和本身两个自然数为其因数的大于1的整数称为素数。除2为偶素数外，其余素数都是奇数。
- 二次剩余：
，9是3的二次方，用7去除平方数9得余数为2，即
。称2是模7的二次剩余。
- 平方剩余码序列
- 平方剩余：
- 设N是一个奇素数，而i是一个与N互素的整数。若
- 平方剩余：
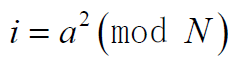
- 有整数解，则称 i 是模 N 的平方剩余。否则，i 就是模 N 的非平方剩余。平方剩余不包括0元素
- 平方剩余与差集：
- 当 N=4t-1为一个素数时（t为整数），则模N的平方剩余（i）就构成一个差集。
- 例子
- 因此若 N=4t-1 为素数，则存在一个周期为 N 的伪随机码序列
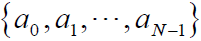，其中：
- 当 N 为奇数时，上面定义的
正是所谓的勒让德符号
- 于是有：
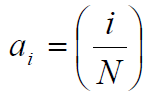
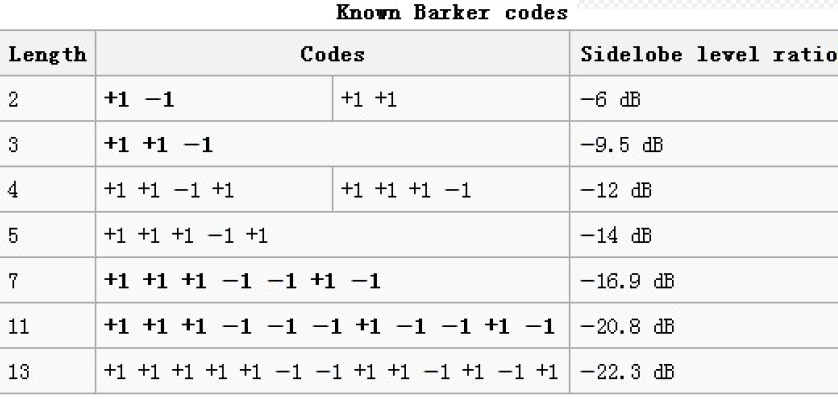
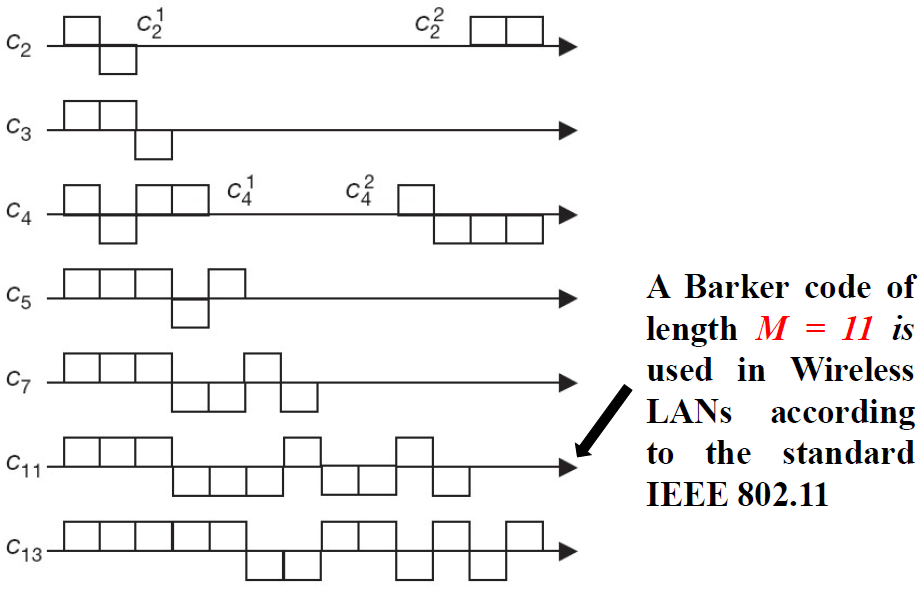
- (Barker Code)
伪噪声序列根据自相关函数的周期性分为：
- 周期序列
- 非周期序列
周期序列
- 伪噪声序列的自相关函数为周期函数，称为周期序列
非周期序列
- 非周期伪随机序列是指序列自相关函数为非周期，具有类似于白噪声自相关函数的序列。例如：数字通信中用的同步头
巴克码就是一类非周期序列
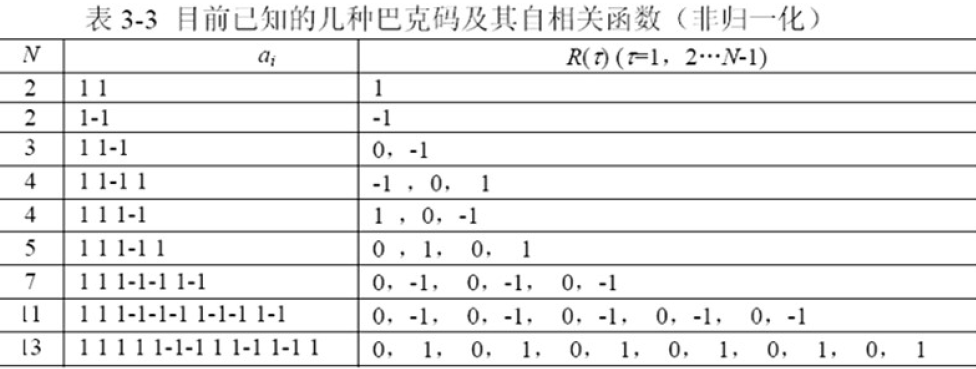
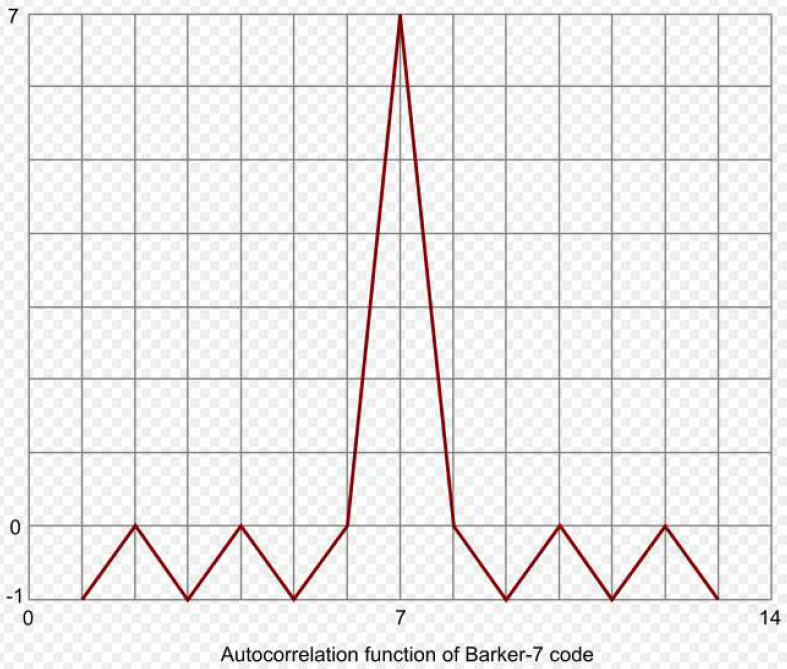
巴克码是一种非周期码，它具有良好的自相关特性，当
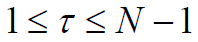时，它的局部自相关函数(非归一化)为
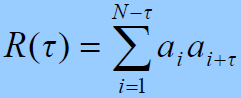
- 且满足下式
- 说明：
- 巴克码的非周期自相关函数共有四个值：在原点处有峰值N，在其它值上，在0，1，-1之间起伏
- 具有类似白噪声的自相关函数
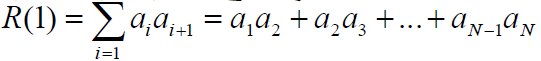
- 性质：（t＝０，．．，n-1）
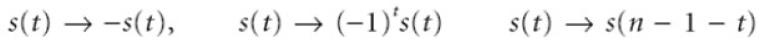
- 目前已知巴克码只有很少几种，且长度较短
3.4 m序列
- m序列是一种具有优良自相关函数，是狭义伪随机序列
易于产生与复制，在扩频技术中得到广泛应用：
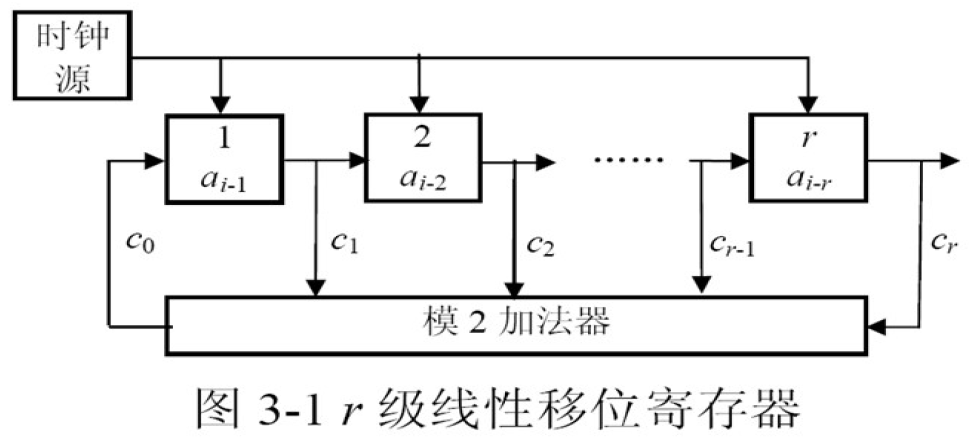
r 级线性反馈移位寄存器的反馈逻辑可用二元域GF(2)上的 r 次多项式表示
- 称为线性反馈移位寄存器的特征多项式
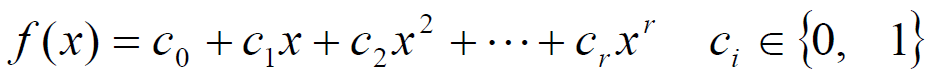
- 线性/非线性移位寄存器
- 动态/静态线性移位寄存器
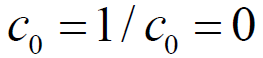
- 退化/非退化移位寄存器
- 线性移位寄存器：(产生m序列)
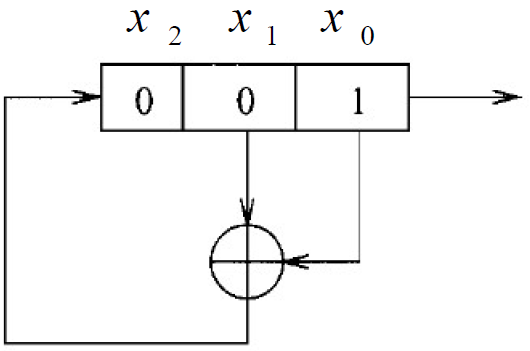
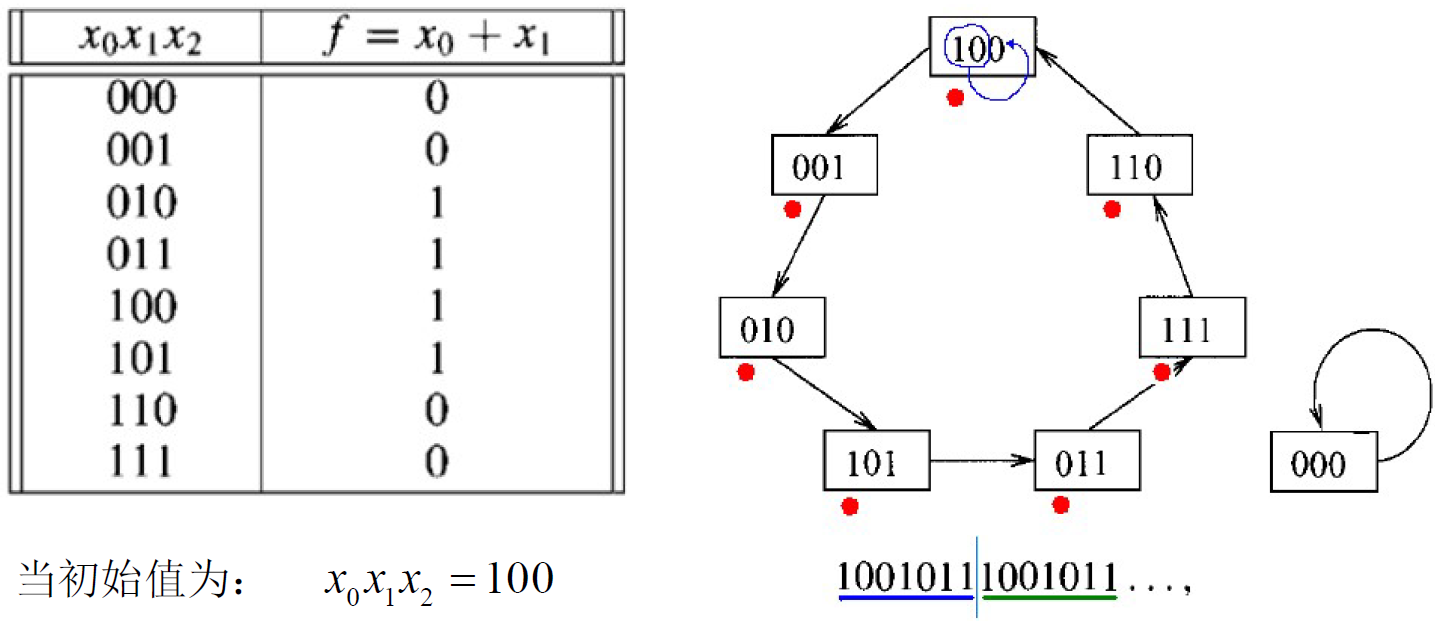
- 动态线性移位寄存器反馈逻辑表示方式：
- 特征多项式
- 递归关系式
- 动态线性移位寄存器的递归关系式：
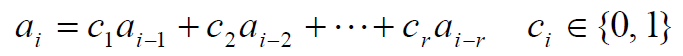
- 它们因应用的场合不同而采用不同的表示方法
- 由r级线性反馈移位寄存器的特征多项式所产生的序列周期为：
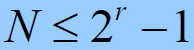
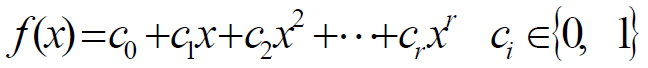
- m序列：
- 若以GF(2)域上 r 次多项式为特征多项式的 r 级线性移位寄存器所产生的非零序列
的周期为
，则称为最大(最长)周期的 r 级线性移位寄存器序列，简称m序列
- 若以GF(2)域上 r 次多项式为特征多项式的 r 级线性移位寄存器所产生的非零序列
- 本原多项式：
- 若由 r 次特征多项式 f(x) 所产生的序列是 m 序列，则称
为r次本原多项式
- 若由 r 次特征多项式 f(x) 所产生的序列是 m 序列，则称
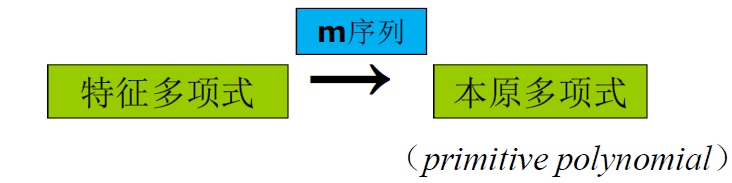
注意：
（1）m序列的随机特性
- 随机序列具有两方面特点
- 具有预先不可确定性，且是不可重复实现
- 具有某种随机的统计特性，主要表现在
- 序列中两种不同元素出现的次数大致相等
- 序列中长度为k的元素游程比长度为k+1的元素游程数量多一倍
- 序列具有类似白噪声的自相关函数，即自相关函数具有
函数形式
- m序列是一种常见的伪随机序列，具有如下特性：
- ① 均衡性
- 在周期
内，元素1比元素0多出现一次 - 元素1出现
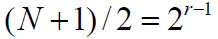次 - 元素0出现
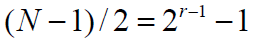次 - 均衡性可减少调制后的载波泄露，使信号更加隐蔽
- 在周期
- ② 游程特性
- 游程：把序列中取值相同的那些相继元素合称为一个游程；游程内元素个数称为游程长度
- m序列游程数为：
个 - 长度为k (1≤k≤r-2)的占
- 长度为k (1≤k≤r-2)的游程中，连“1/0”的游程各占一半
- r-1个连“0”游程为一个
- r个连“1”的游程为一个
- ① 均衡性
- 随机序列具有两方面特点
- 例子
- ③ 位移相加特性- m序列与其位移序列的模2加序列仍是此m序列的另一位移序列，即：
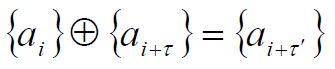
（2）自相关函数
- m序列与m码：
- 将m序列的每一比特变换为宽度为
、幅度为1的波形函数 - 当m序列为0元素时，波形函数取正极性，否则取负极性
- 变换后，周期为N的m序列就变为码元宽度为
、周期为
的m码
- 将m序列的每一比特变换为宽度为
- m序列自相关函数：
- m序列与m码：
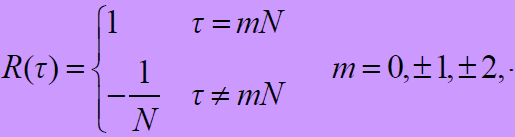
- m码自相关函数：
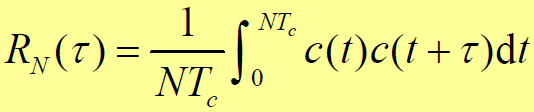
- m码引入了时间概念
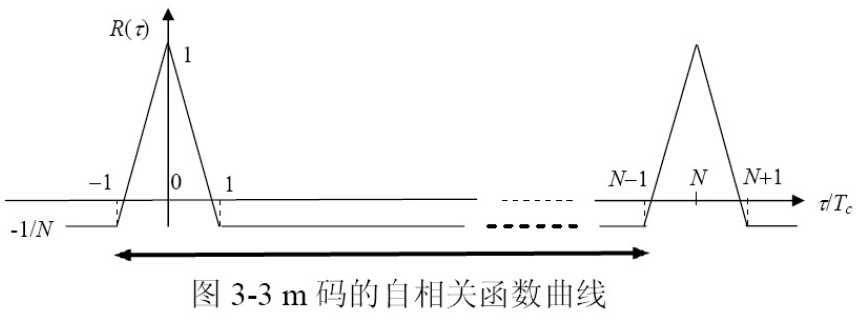
- 周期为
的码的自相关函数是一周期函数
- 自相关函数 = 高度为(N+1)/N的周期三角形脉冲 – 幅度为1/N的直流分量
- 在
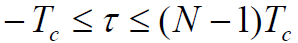区间（一个周期
）内m码的自相关函数可表示为：
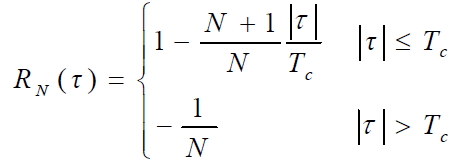
- 利用下式
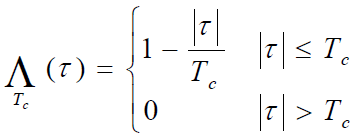
- 可得：m码自相关函数为
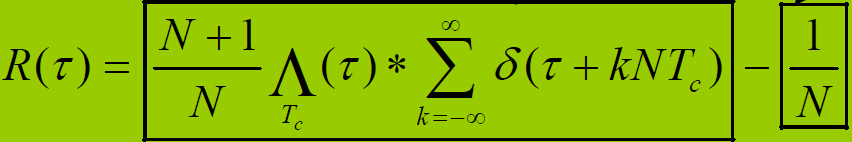
(3) m序列的功率谱密度函数
- 由傅氏变换：
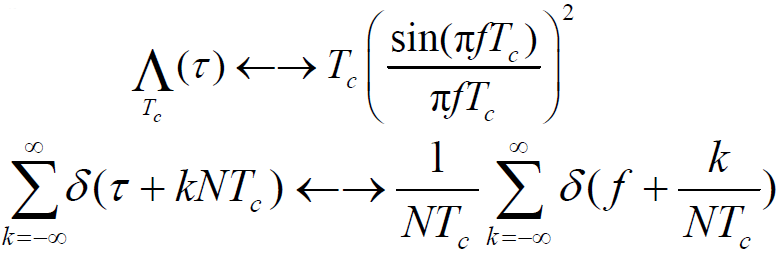
- 得：三角函数的功率谱密度函数：
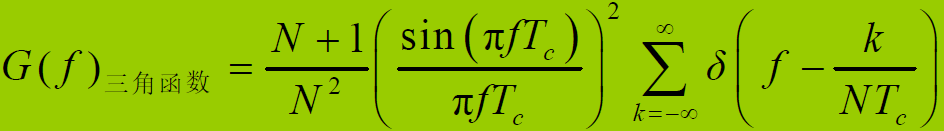
- 直流分量的功率谱密度：
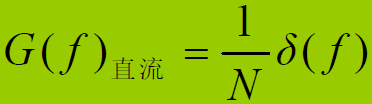
- m码功率谱密度函数：
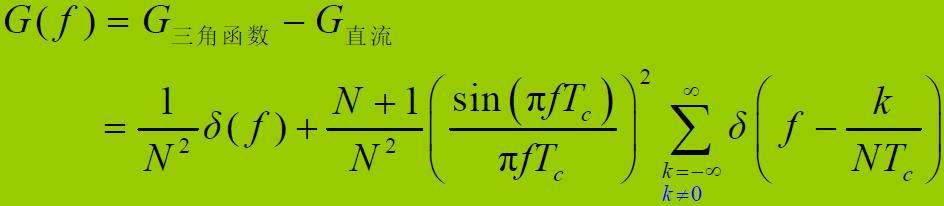
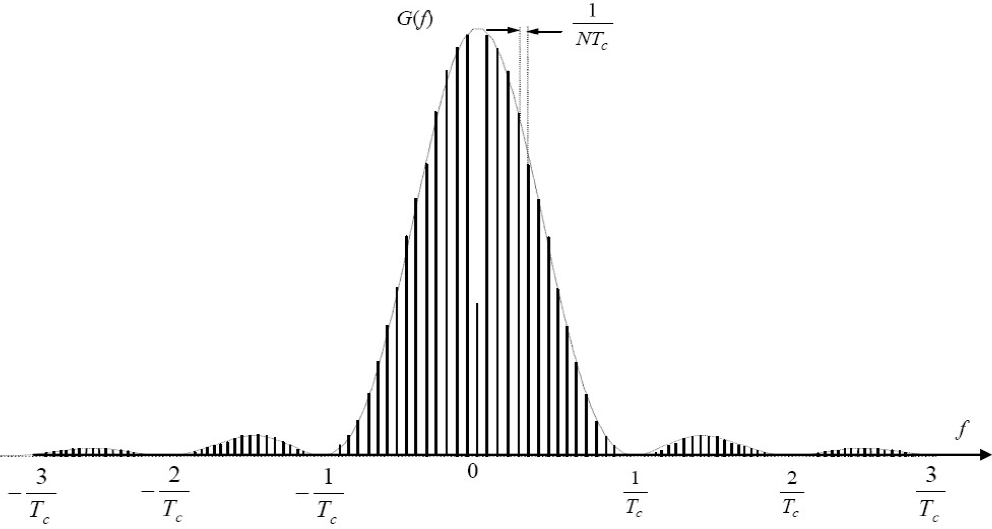
- 功率谱密度函数特点：
- ① m码的功率谱是离散(线状)谱，谱线间隔为
，即：m码的功率谱由基波与各次谐波组成，基波频率为
，是m码时钟频率（位同步频率或称为码速率）的 1/N 倍 - ② m码的功率谱密度函数具有抽样函数
的包络，第一个零点在 k=N 处，即
，第二个零点 k=2N，以此类推，若n为整数时，
，有
。m码频谱分量中不包含位同步信号分量的信息。 - ③ m码的功率谱的带宽（通常定义为第一个零点处的频率）由码元持续时间 Tc 决定，带宽
（单边），与码的长度N无关。 - ④ m码的直流分量与
成反比。当 m 序列的长度
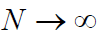时，直流分量，谱线间隔，m码的功率谱由离散谱向连续谱过渡，伪随机码过渡为随机码。
- ① m码的功率谱是离散(线状)谱，谱线间隔为
(4) m序列的互相关函数
- 自相关函数具有理想的双值特性
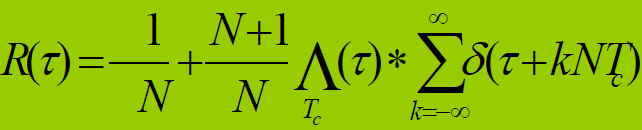
- 互相关函数：
- 研究对象：长度相同而序列结构不同的两个m序列之间的相关函数。
- 性质:
- （1）m序列互相关函数是多值函数，3值，4值，多值
- （2）m序列互相关函数值不具有简明解析公式，只有统计特性
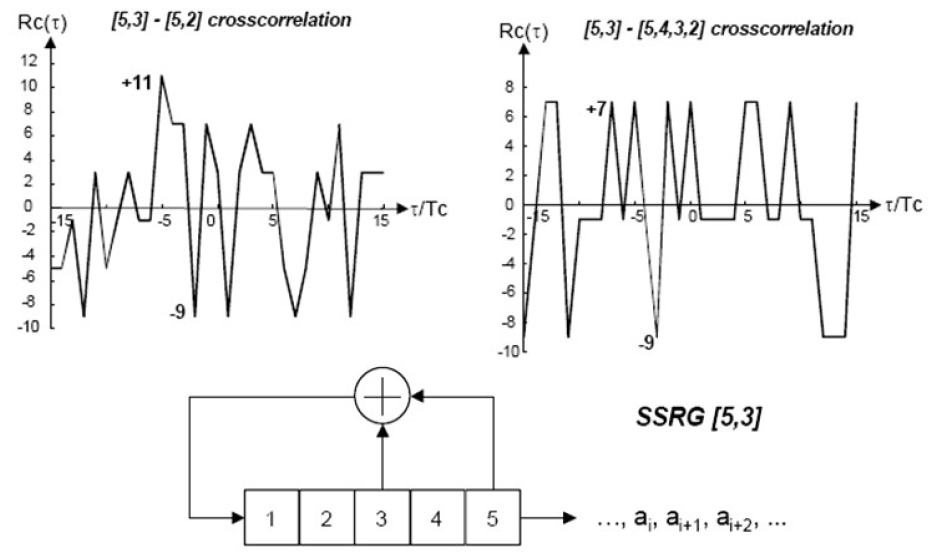
- 互相关函数值统计特性：
- 均值：
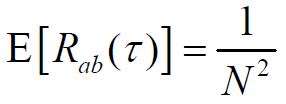
- 方差：
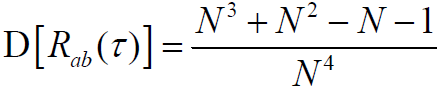
- 互相关函数值的界:
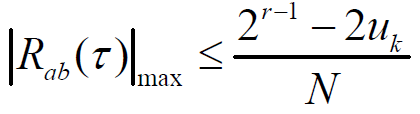
- 是这组m序列特征多项式首根中幂指数的最小者
- 特征多项式首根
- 若a是
阶有限域 GF(2) 的一个本原元，那么GF(2)的一个 r 次不可约多项式 f (x) 的 r 个不相等的根都可表示成a的幂次 - 设r个根为：
- 若a是
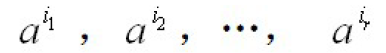
- 并假设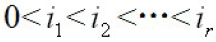成立，则定义是 f (x) 的首根
3.4.3 m序列构造
- 构造m序列的线性移位寄存器方法：
- （1）确定本原多项式
- （2）根据本原多项式构造出m序列移位寄存器的结构逻辑图
- 本原多项式的寻找：
- 在所有r次多项式中去掉可约多项式，在剩余的r次不可约多项式中，根据本原多项式定义
- 用试探方法，看是否产生m序列。若是，则为本原多项式；若否，则不是。
- 编程实现。
- 互反多项式：
- r次多项式 f (x) 的互反多项式定义为：
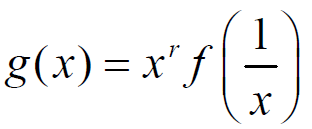
- 性质：
- 不可约多项式的互反多项式为不可约多项式
- 本原多项式的互反多项式也为本原多项式
- 例子
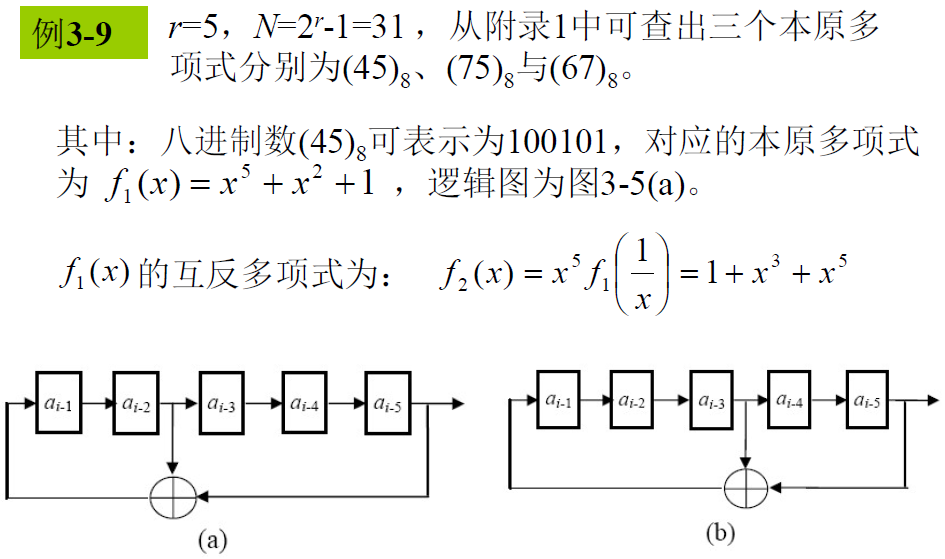
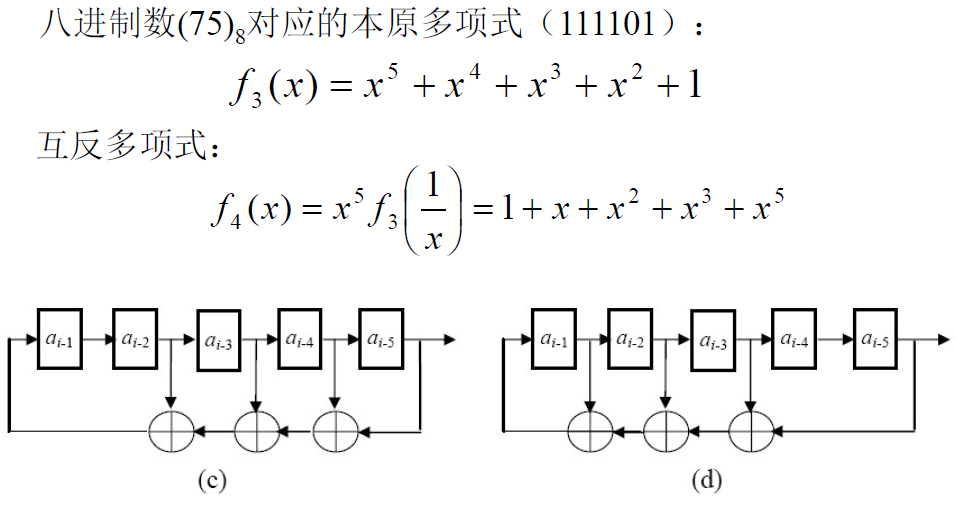
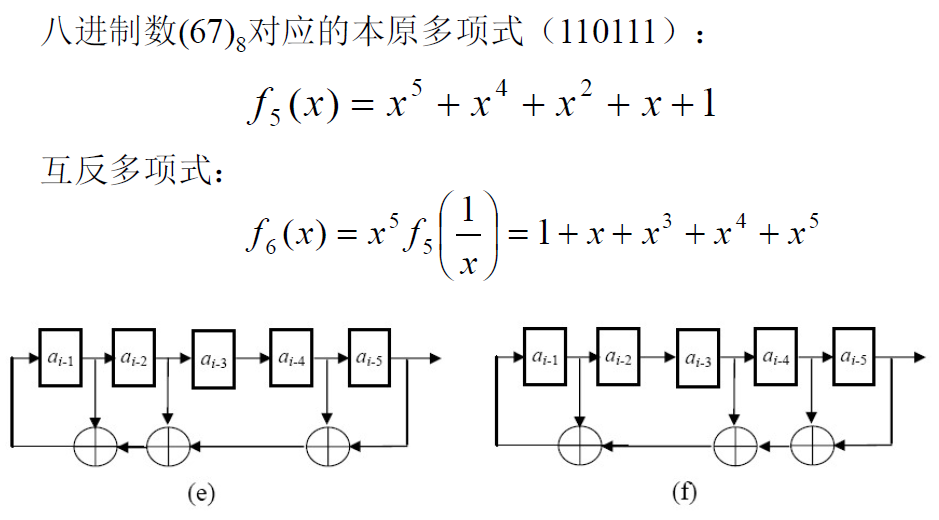
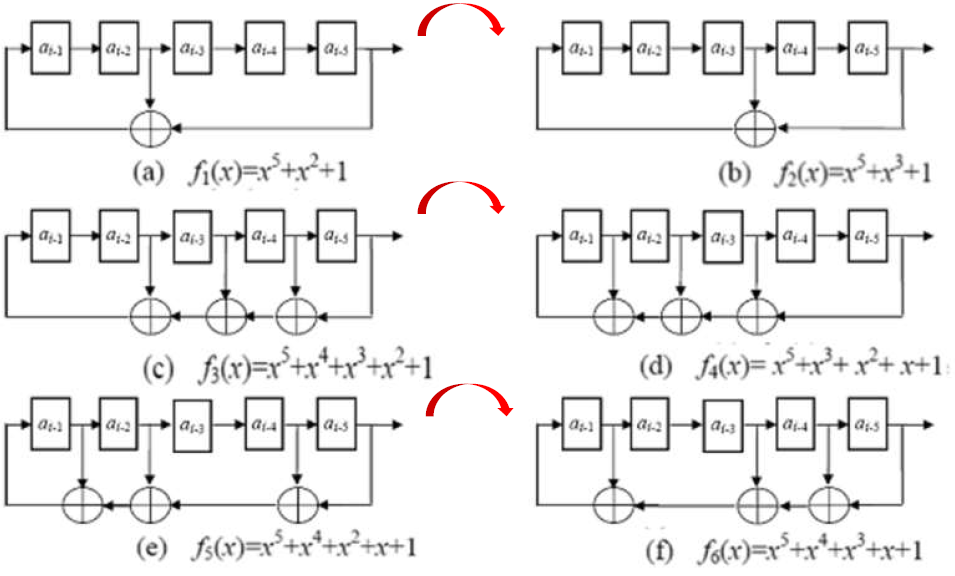
- 问题
- 某些情况并不关心产生m序列移位寄存器的具体结构，而只关心m序列
，即移位寄存器的输出序列
- 某些情况并不关心产生m序列移位寄存器的具体结构，而只关心m序列
- 解决方法
- 可以通过求解输出序列多项式G(x)的方法得到
- 输出序列多项式G(x)的系数就是所要求的输出序列
- 多项式G(x)称为序列
的生成多项式或序列多项式 - 在给定特征多项式与移位寄存器初始状态的情况下，移位寄存器的输出序列被唯一确定
- 性质
- 【在初始状态为100…0的条件下】，线性移位寄存器的序列多项式G(x) 与特征多项式f(x)关系为：
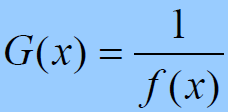
- 注意概念区分：
- 例子
- 采用长除法的周期问题
- 长除时，进行到余式为某一单项式时即可，这是因为m序列周期=N
- 序列多项式G(x)为：
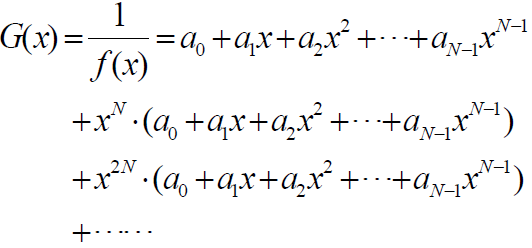
- 对应的输出序列为：
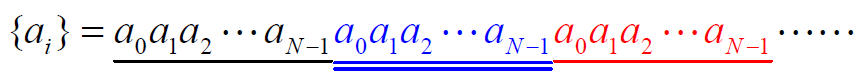
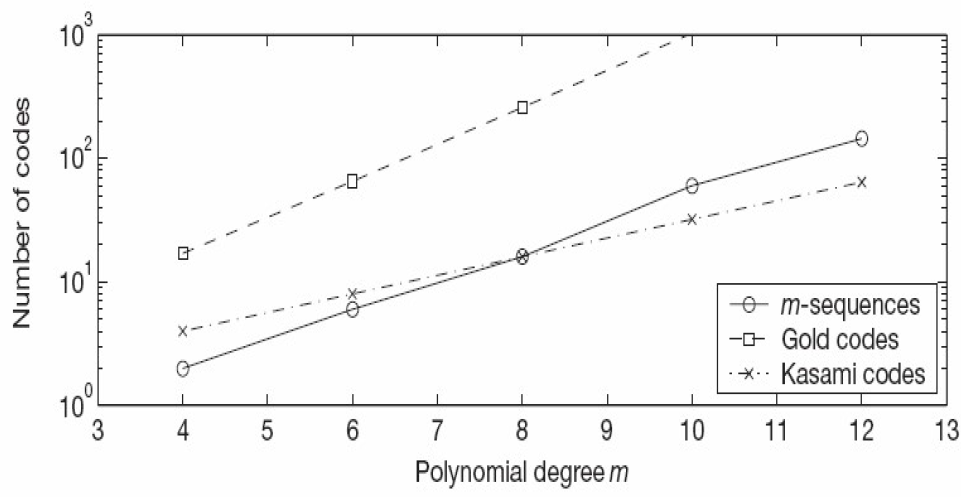
- m序列数量：
- 对于 r 级线性移位寄存器，可以证明能产生周期为
的m序列的总数为：
- 对于 r 级线性移位寄存器，可以证明能产生周期为
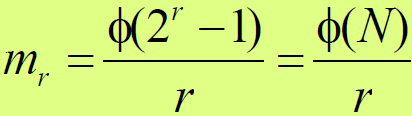
- 其中：
为欧拉(Euler)数，它等于包括1在内的所有小于N的，且与N互质的正整数的个数 - 公因数只有1的两个数，叫做互质数
- 例子
3.5 Gold序列
3.5.1 m序列优选对
- 本征取样：
- 一个m序列的取样不一定产生另一个m序列，当取样产生另一个m序列时，这种取样被成为本征取样
- 利用奇数为q的本征取样可以生产所有周期为N的m序列
- m 序列对的互相关值
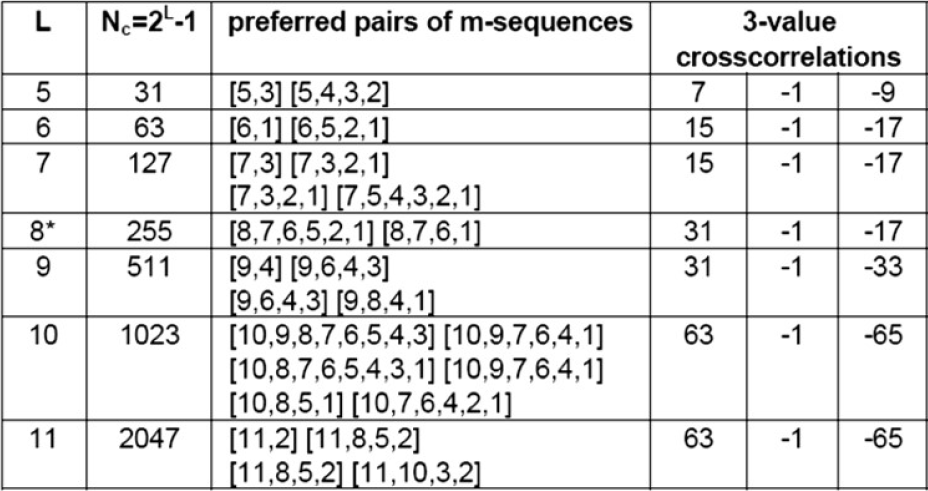
- 可能是三值、四值或者多值的。一些特殊的m序列对的互相关是三值的，此三值为：
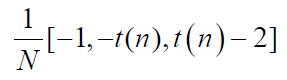
- 其中，
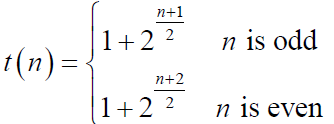
- 码序列的周期为
，被称为m序列优选对 - 注意：在构造Gold 序列集时，必须先找到m序列优选对
- v 和 u 是 m 序列优选对的充分条件如下：
- 序列阶数 n 的约束：对 4 取模时，余数 n ≠ 0（即 n 为奇数）；或对 4 取模时，n = 2
- v = u(q)，q 为奇数并取下列值之一
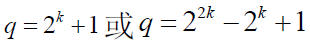
- 3.
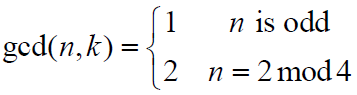
- m序列优选对（Preferred Pair）定义
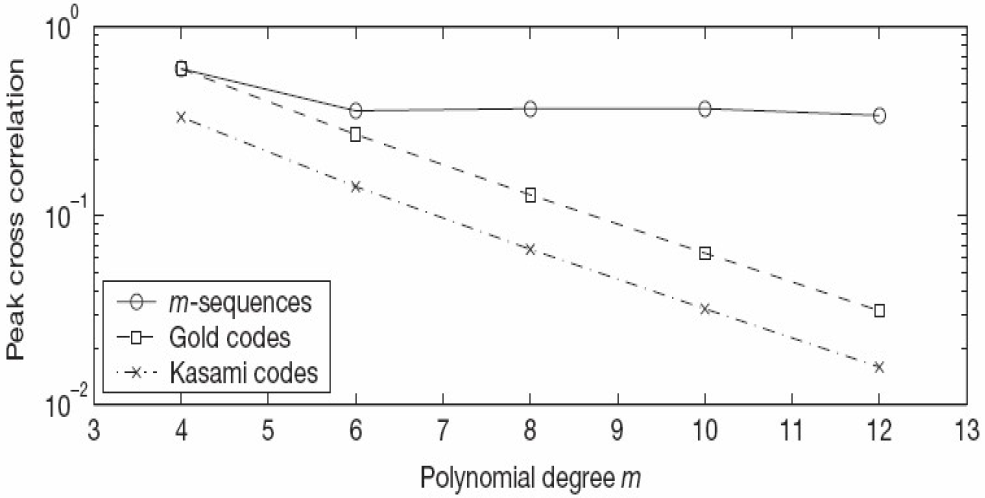
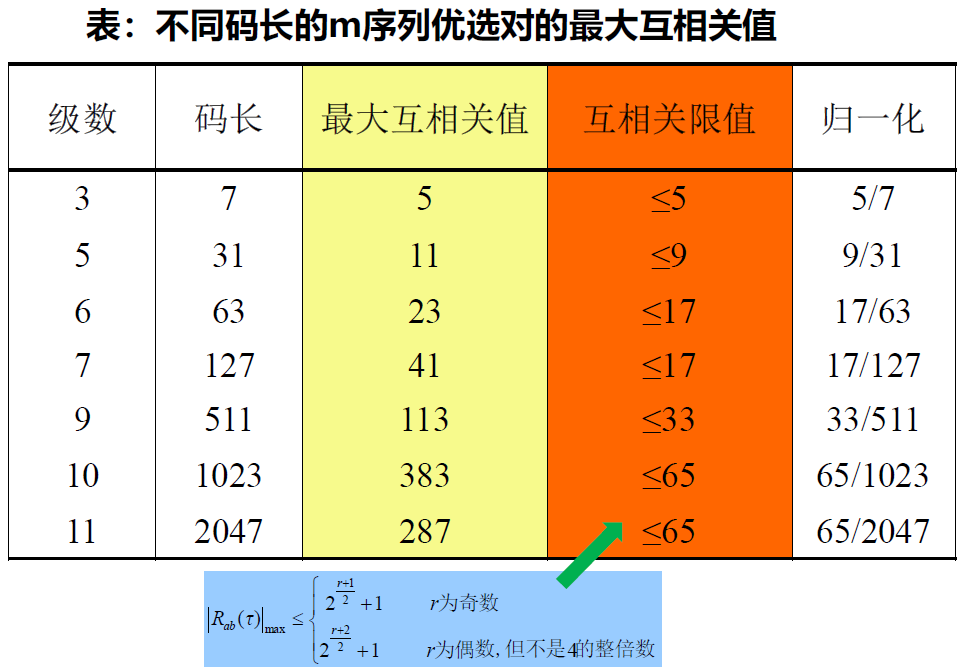
- 在m序列集中，其互相关函数绝对值的最大值（称为峰值互相关函数） 最接近或达到互相关值下限（最小值）的两条m序列
- 设
和
分别是对应于 r 次本原多项式
和
所产生的m序列 - 若它们的峰值互相关函数满足上式，则m序列
和
构成m序列优选对- 例子
- m序列的特点：
- 具有优良伪随机性和双值自相关特性，但互相关特性不是很好，且数量少。
- 构成CDMA系统时，由于互相关特性不理想，系统内多址干扰影响增大，且可用地址码数量较少。
- 地址码的选择：
- 扩频通信是用码的形状差异来区分通信地址的一种选址通信方式。
- 地址码性能的好坏，直接关系系统性能优劣。
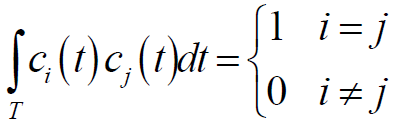
- 一般，对于不同的网其地址码是不同的，期望不同网的地址码互相关值应为零，即地址码正交。
- 对地址码的一般要求：
- （1）自相关、互相关和部分相关特性良好。即要求码的自相关旁瓣、互相关和部分相关值要尽可能小，以便在检测地址码是有最大的分辨率。
- （2）码序列要多。直接影响系统的组网能力及频谱利用率的高低。在满足条件1的情况下，码序列越多越好。
- （3）有一定的长度。码序列越长，越接近于随机序列，从而抗干扰的性能越强。
- （4）易于实现系统的同步，捕获时间要快。
- （5）易于产生、设备简单、成本低。
Gold序列
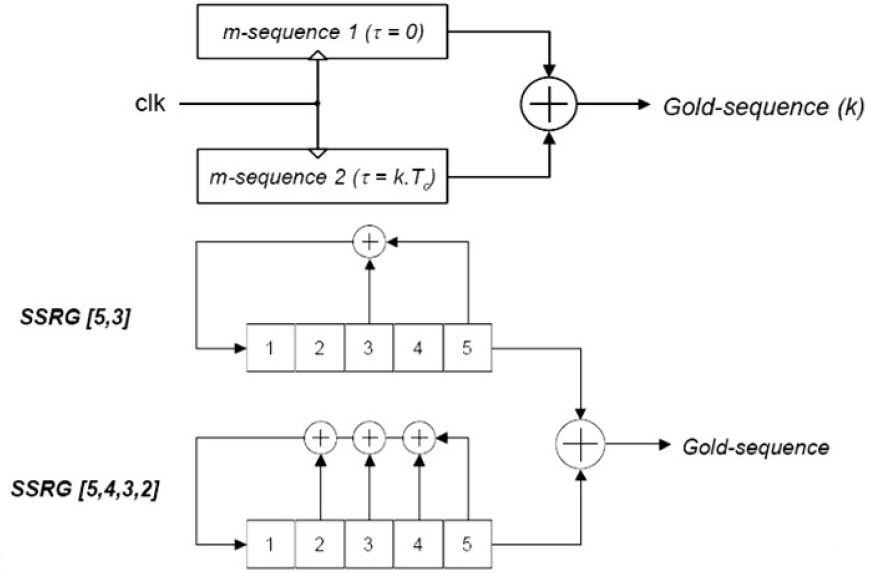
1967年，R·Gold指出：“给定r级移位寄存器，总可找到一对互相关函数值是最小的码序列，采用移位相加方法构成新码组，其互相关旁瓣都很小，且自相关函数和互相关函数均有界”。此序列称为Gold码（Gold序列）
Gold码构成：
- Gold序列是m序列的复合序列，由两个码长相等、码时钟速率相同的m序列优选对的模2和序列构成。
- Gold码数量：
- 每改变两个m序列相对位移就可得到一个新的Gold序列。当相对位移0，1，2，…，N -1个比特时，就可得到
个Gold序列，加上原来的两个m序列，共有
个Gold序列，即
- 每改变两个m序列相对位移就可得到一个新的Gold序列。当相对位移0，1，2，…，N -1个比特时，就可得到
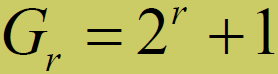
- 这
条Gold码称为一个Gold码族- Gold码构造方式：
- 产生Gold序列的移位寄存器结构有两种形式：模2和型；乘积型；
- 模2和型：
- 直接求两m序列优选对输出序列的模2和序列。
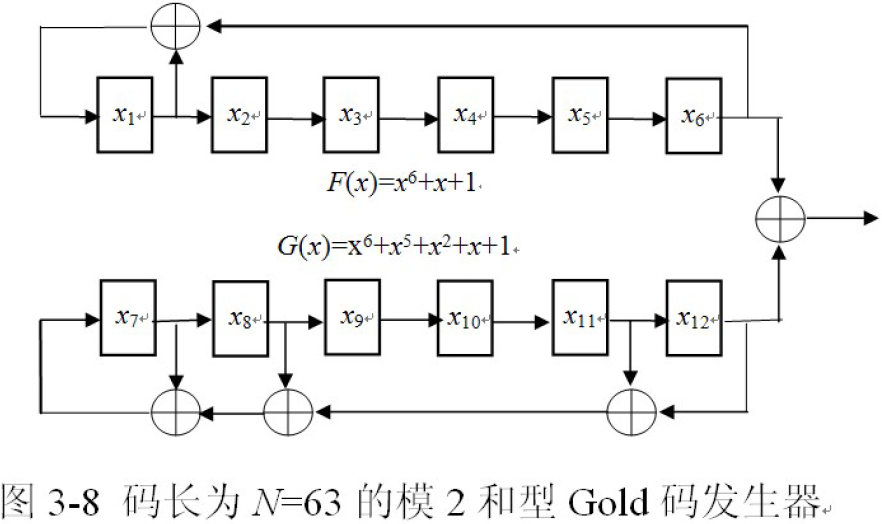
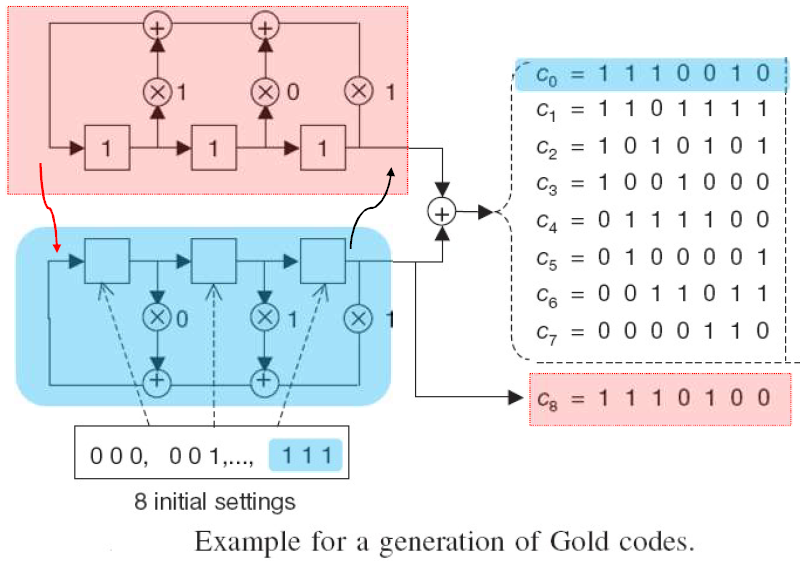
- 乘积型：
- 将m序列优选对的特征多项式乘积作为新的特征多项式，据此2r次特征多项式构成新的线性移位寄存器
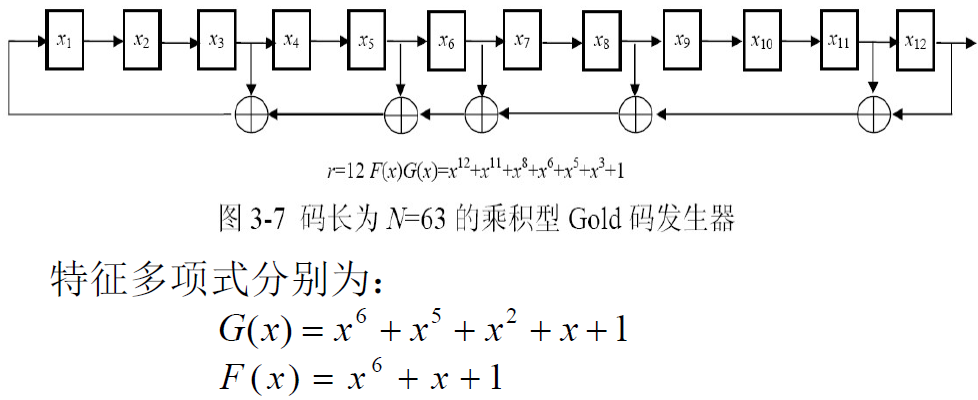
两种结构特点：
- 两种结构完全等效
- 复码的周期是组成复码的子码周期的最小公倍数。由于组成复码Gold序列的子码的周期都是
- 故Gold序列周期是:
Gold码相关特性：
- ① Gold码族中
个序列不再是m序列，不再具有m序列的特性Gold码族中任意两序列间的互相关函数满足：
- ① Gold码族中
- 因此，Gold码族中任一码序列都可作为地址码。地址数大大超过m序列。在多址技术中得到广泛应用
- ② Gold序列族中，除了两个m序列外，其它序列都具有三值的自相关和互相关特性
- 当 r 为奇数时，码族中约有50%的码序列有很低的互相关函数值(-1)（非归一化）
- 当 r 为偶数（非4整倍数）时，码族中约有75%的码序列有很低的互相关函数值(-1) （非归一化）
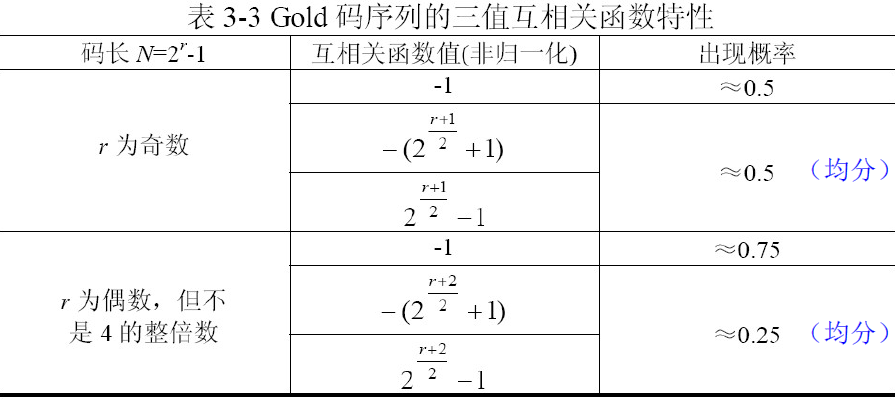
- 归一化互相关函数值：
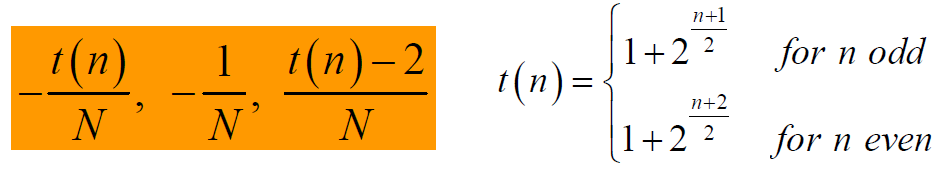
- ③ Gold序列自相关函数值的旁瓣取三值，互相关函数值也取三值，只是出现的位置不同
- Gold码族同族内互相关函数取值已有理论结果，但不同族之间互相关函数的取值尚无理论结果
不同Gold码族之间的互相关函数取值已不是三值而是多值，且互相关值已大大超过同族内的互相关值
Gold码相关特性实例：
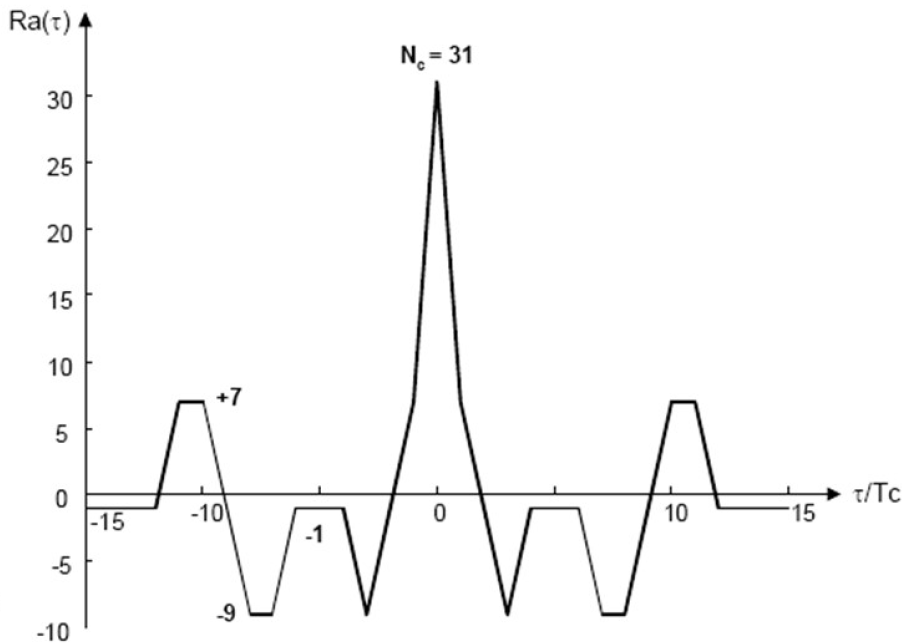
- Gold码自相关特性：
3.5.3 m序列优选对寻找
- 优选对构造方法1：
- 若 a 是
阶有限域 GF(2) 的一个本原元， 
与
是
阶有限域GF(2)上的 r 次本原多项式，a 是
的首根，取
- 若 a 是
- 使
为 r 次本原多项式
的一个根，则以 r 次本原多项式
与
为特征多项式的m序列就构成m序列优选对- 例子
- 优选对构造方法2：
- 若 a 是
阶有限域GF(2)的一个本原元， 
与
是
阶有限域GF(2)上的 r 次本原多项式，
是
的首根，t 按照下式取值，令 kt 的共轭类首元
为 r 次本原多项式
首根的幂指数，即它的首根为
，则：以本原多项式 
与
为特征多项式的 m 序列构成 m 序列优选对
- 若 a 是
- kt的共轭类首元：
- 对于任意正整数 kt ，模
运算后，可用 r 位二进制数表示为：
- 对于任意正整数 kt ，模
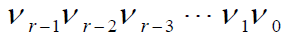
- 将其循环移位，得到一组（共r个）二进制数：
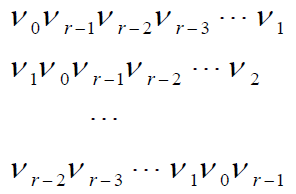
- 称为kt的共轭类；其中最小者称为kt的共轭类首元，用符号来表示
- 例子
- 小结：优选对寻找方法
- 根据两种寻找m序列优选对方法可知：对于给定长度N（或级数r），由于采用不同寻找方法，得到的m序列优选对不相同，由此构成的Gold序列族也不同。
- 现已证明：对级数为【r＝5 ，6，7，9，10】的所有m序列来寻找m序列优选对，有：
- ① 若本原多项式
与
产生的m序列构成优选对，则它们的互反多项式
与
产生的m序列也构成一优选对 - ② 若
与
产生的m序列构成优选对，则
与
产生的m序列也构成一优选对
- ① 若本原多项式
3.5.4 平衡Gold序列
- Gold码平衡性
- 平衡码序列：在一周期内，平衡码序列中1码元与0码元的个数之差为1
- 非平衡码序列：在一周期内，非平衡码中1码元与0码元的个数之差多于1
- 平衡Gold码优点：
- 扩频通信中，扩频码平衡性(序列中0与1的均匀性)影响系统质量，平衡码具有更好的频谱特性。
- 【在DS-SS系统中】，码的平衡性与载波抑制度有密切关系。码不平衡时直接序列系统的载波泄漏增大，从而破坏扩频通信系统的保密性、抗干扰与抗侦破能力。
非平衡码使载波抑制性能下降一半(分贝数)，增加码长对载波抑制性能改善不是十分明显。在DS-SS系统中应选用平衡Gold码
3.5.5 平衡Gold码产生方法
平衡Gold码产生条件：
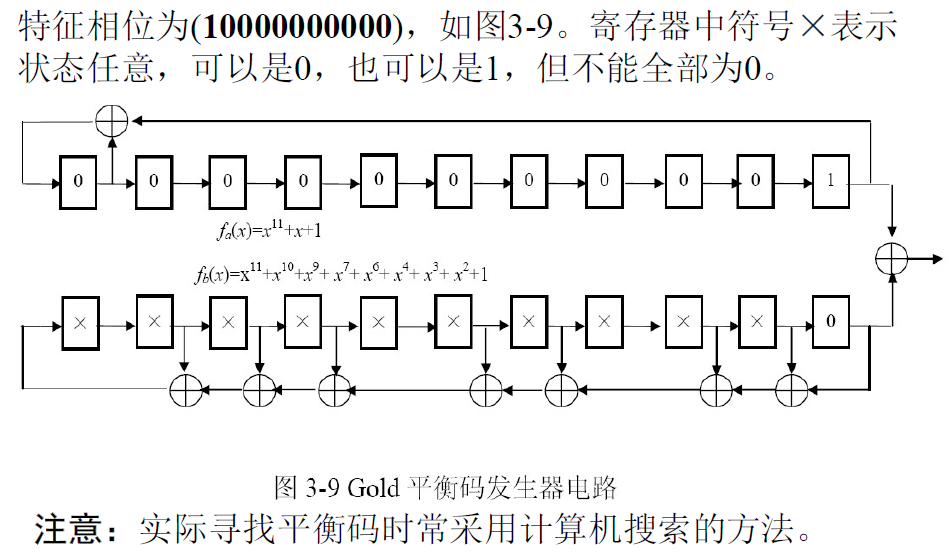
- m序列优选对处于特定的相对相位状态上时，才能产生平衡Gold码。此相位状态称为特征相位。
- 特征相位：
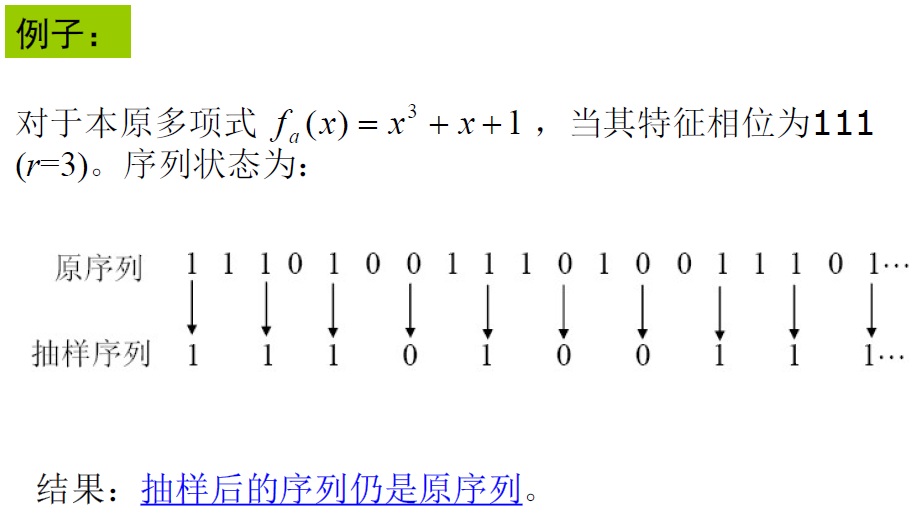
- 为寻找平衡码，R·Gold给出特征相位描述：每一个最大长度序列都具有特征相位（序列的初始状态），当序列处于特征相位时，具有每隔一位抽样与原序列一样的特性。
- 例子
- 特征相位求取：
- 设序列
的特征多项式
是一个 r 次本原多项式，其特征相位由
之比来确定 
是生成函数，其次数等于或小于 r，定义如下：
- 设序列
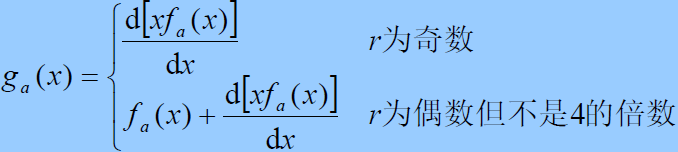
- 特征相位多项式：
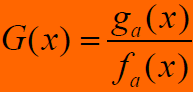
- 通过对式长除法可得到特征相位
- 例子
- 平衡Gold码产生方法：
- 设序列
和
是一对优选对 - ① 选一参考序列
，使之按下式，求出生成函数
- 设序列
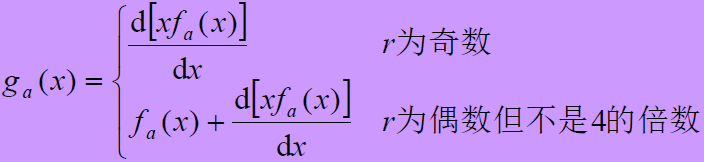
- ② 根据下式求特征相位，使序列
处于特征相位上
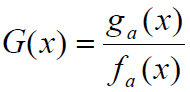
- ③ 设置位移序列
，使序列
的初始状态第 r 级必须为 0，以对准序列
的初始状态第 r 级的1 - 按照上述方法就可以产生平衡Gold码
- 说明：
- 生成平衡Gold码条件：
- （1）获得一对m序列优选对；
- （2）使一个m序列处于特征相位；
- （3）使另一个m序列的相位与之保持特定关系
- 两个m序列的第 r 级（最高位寄存器）状态相异
- 由于处于特征相位的m序列的第r级一定为1，故另一个m序列的第r级为0就可生成平衡Gold码
- 为了得到平衡Gold码，还需要确定m序列优选对间的相位关系
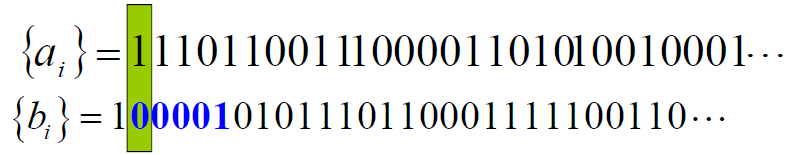
- 例子
3.5.6 Gold码应用
- GPS系统(卫星导航定位系统):
- Global Positioning System (GPS) 系统的空间段由24颗卫星组成
- 分布在六个不同的轨道上（20,000 km左右）
- GPS系统两个频点：
- Link1 （L1）
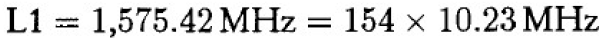
- Link2 （L2）
- Link1 （L1）
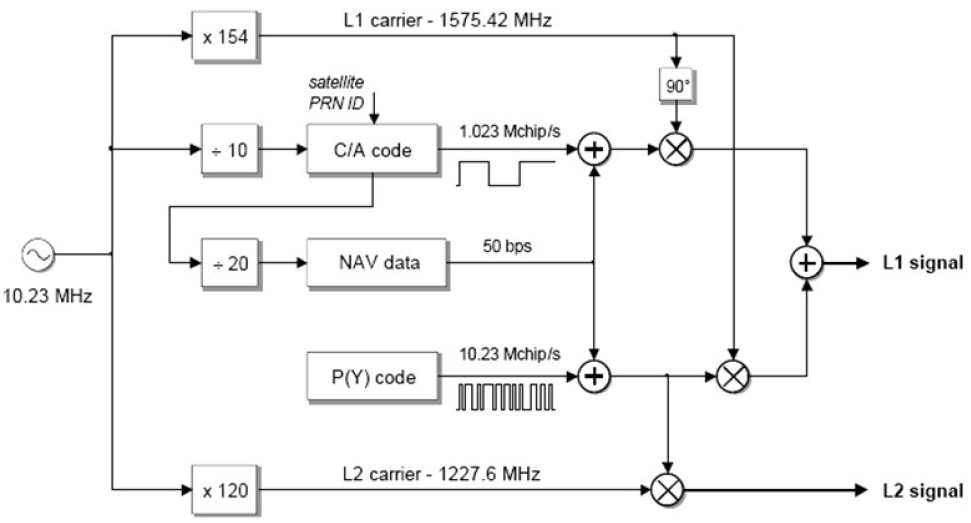
- GPS系统有两种码：
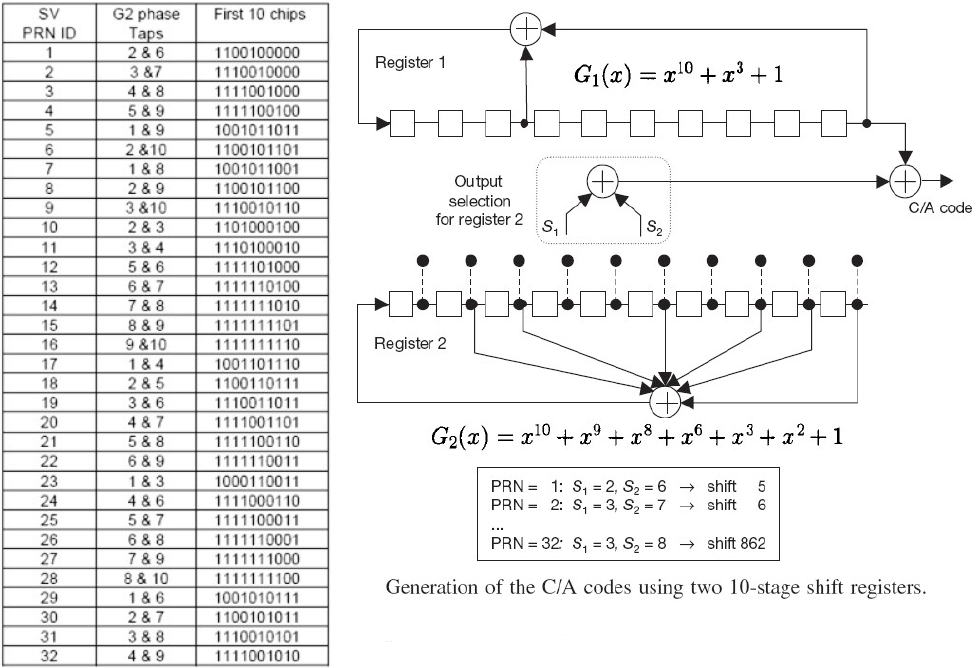
- C/A码：(coarse/acquisition or clear/access codes) 码速率为：1.023Mchip/s；民用；Gold码；
- P码：(precision or protected code) 码速率为：10.23Mchip/s；军用；
- Link1中第i个卫星的信号可以表示为：
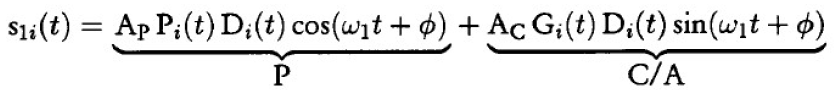
- 其中：
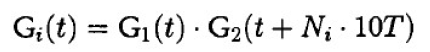
- 特点：不同编号的卫星通过分配不同的Gold码加以区分
- GPS系统信号组成：
3.6 Kasami 序列
3.6.1 Kasami小集
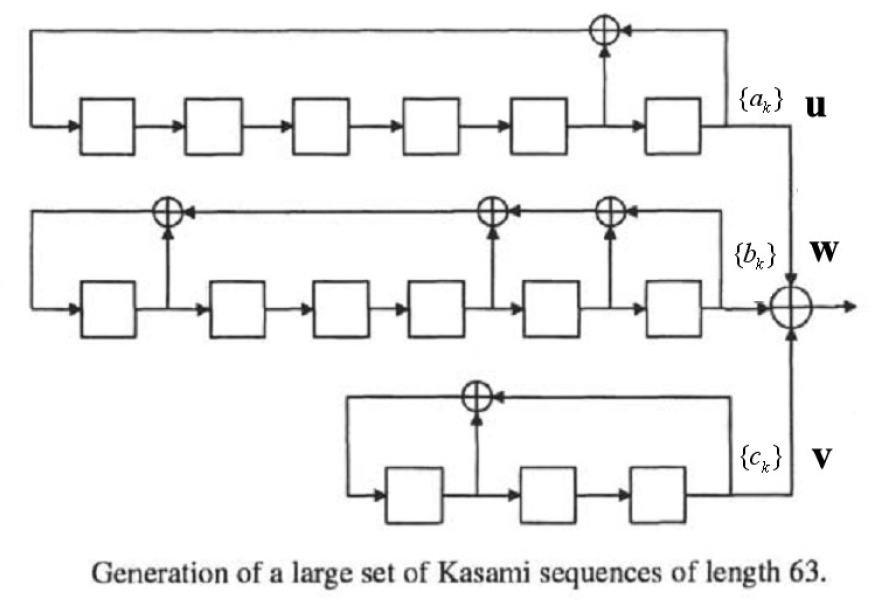
- 构成方法
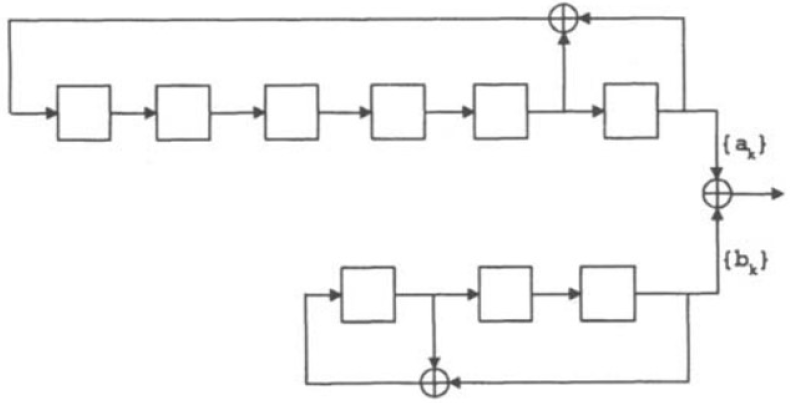
- 序列u
- m序列u由本原多项式
生成 - 该本原多项式的周期为
，n为偶数
- m序列u由本原多项式
- 序列v
- v序列由本原多项式
生成 - 被u通过计算提取
- v序列由本原多项式
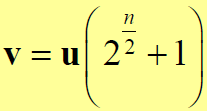
- 序列v的性质
- v是一个m序列
- 周期为
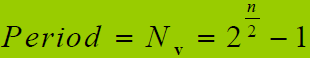
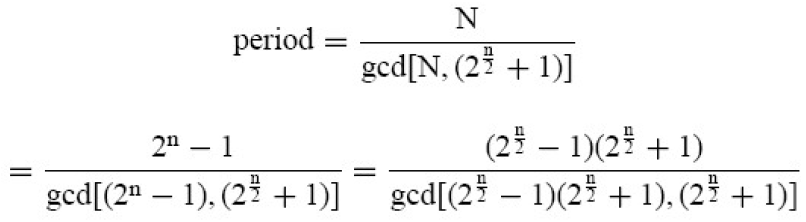
- Kasami小集序列是用 u 与 v 的所有可能相位的模相加生成的本原多项式h(x)=hu(x)hv(x)
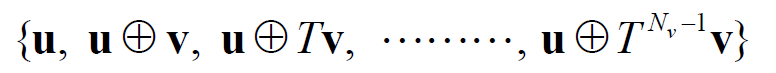
- 其中
表示m序列v被
移动相位 - 该集合包含有
个序列 - 每个周期为N且具有三值相关函数[−1，−s(N)， s(N)−2]的序列，其中
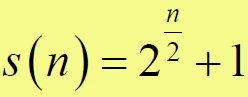
- 构造方法
- 序列u由偶数次本原多项式hu(x)生成，周期为n
- 序列
是由周期为n的多项式 hw(x) 对 u 的抽取 - 序列
是n/2次的原多项式 hv(x) 对 u 的抽取，周期为
- 由原多项式h(x)=hu(x) hv(x) hw(x)生成Kasami序列的大集合
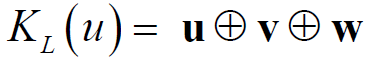
- 周期为
的大小为
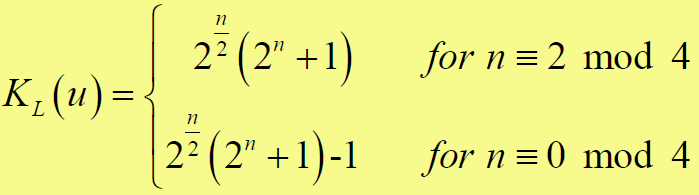
- 序列的自相关和互相关函数都取集合中的一个值
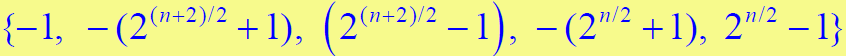
- 相关性的最大幅度为
- 例子
- 注意：即使元素数量增加，Kasami序列大集合的最大相关值仍与Gold序列的最大相关值保持一致。
若有收获，就点个赞吧
0 人点赞
