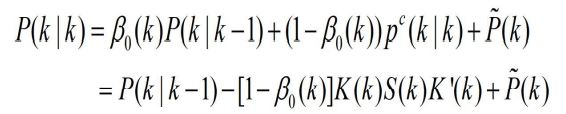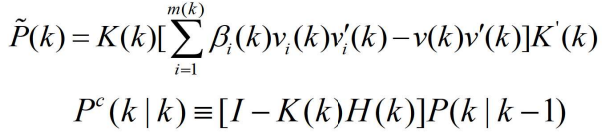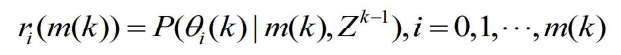• 目标跟踪领域的一个研究重点是如何解决杂波，干扰目标跟踪问题。
• 在可用的算法中，有代表性的是概率数据关联算法(PDAF),在杂波环境下有很好的跟踪性能。

4.1 概率数据关联滤波器

4.1.1 预备知识

• 考虑线性和量测方程描述的混合系统:

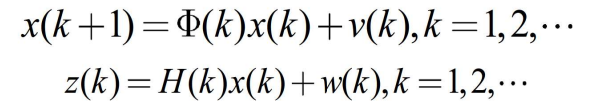
• 其中，表示 k 时刻的状态向量，表示k 时刻的观测向量，表示状态转移矩阵，H(k )表示量测矩阵，v(k)和 w(k)是零均值相互独立的白色高斯过程噪声。v(k)和w(k) 分别具有已知方差

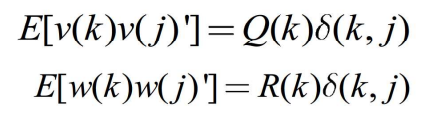
• 其中

4.1.2 概率数据关联滤波器的基本思想

• 概率数据关联理论的基本假设是,在杂波环境下仅有一个目标存在，并且这个目标的航迹已经形成。
• 如果每个时刻的有效回波只有一一个，则关联问题就变成经典的卡尔曼滤波问题。
• 但是，在杂波环境下，由于随机因素的影响，在任一时刻，某一给定目标的有效回波往往不止一一个。
• 这样就产生了一个无法回避的问题：究竟哪一一个有效回波是来自目标的?
• 为解决这个问题所采用的一种方法是所谓的“最近邻”方法，即简单地认为离目标预报测量最近的有效回波源于目标，其余有效回波都源于杂波干扰

• 另一种方法认为所有有效回波都可能源于目标，只是每个有效回波源于目标的概率有所不同，这正是我们本章要研究的概率数据关联算法。

• 设

• 表示传感器在k时刻确认的量测集合
• 表示在k时刻确认的量测的个数
• 表示直到时刻k的累积量测集
• 表示是来自目标的正确量测的事件
• 表示传感器所确认的量测没有一个是正确的事件
• 则有

• 表示在 k 时刻，第 j 个量测是来自目标这一事件的概率(量测源于目标的概率)，由的定义易知是事件空间的一个不相(k)交完备分割，从而有

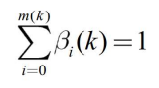
• 令

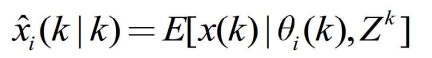
• 表示在事件出现的条件下的更新状态估计，则应用全概率公式，有

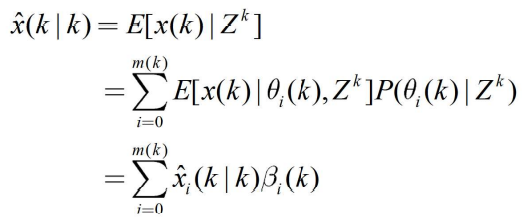
• 令x(k|k-1)表示根据从1到k-1时刻所有以往量测数据对k时刻数据x(k)所作的预报，则应用卡尔曼滤波器得

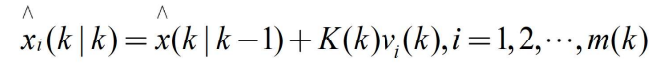
• 其中

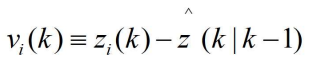
• 在处理预报和滤波问题时经常要用到
• 它给出了中所含有真正全新的信息，故称其为量测 i 的新息(Innovation)
• 增益 K(k) 和标准滤波器的一样。对于 i=0, 即如果没有一个量测是正确的，则

• 得概率数据关联滤波器的目标状态更新估计为

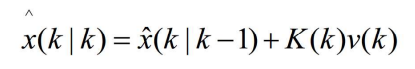
• 其中

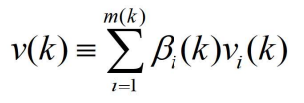
• 称为组合新息
• 目标状态更新估计相应的协方差为

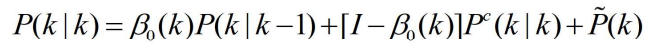
• 其中

4.1.3 关联概率的计算

• 由式，第i个量测在k时刻与目标关联的概率为

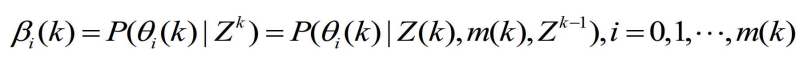
• 应用贝叶斯公式和乘法定理得

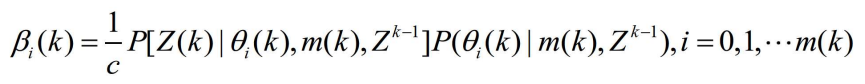
• 其中

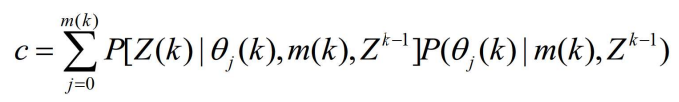
• 概率数据关联滤波器依据的3个基本假设是:
  • (1) 假量测在跟踪波门中服从均匀分布，即

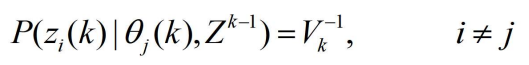
  - 其中![](https://cdn.nlark.com/yuque/__latex/e60bc493da0ec3fc7e3b8414758ee218.svg#card=math&code=V_k&id=a3Z8h)表示跟踪波门的体积

• (2) 正确量测服从正态分布，即

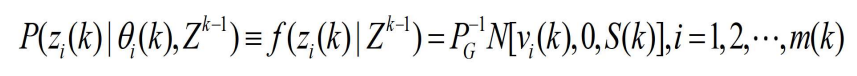
  - 其中

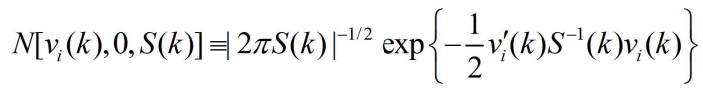
  - ![](https://cdn.nlark.com/yuque/__latex/1b32d078a58b149739c80c76f5c3d1f5.svg#card=math&code=P_G&id=pvZpo)表示正确量测落入跟踪门内的概率

• (3) 在每一个采样周期至多有一个真实量测，这个事件发生的概率为
  • 对于i=0，即所有确认量测都不正确的情形。根据第一个假设,在已知 k 时刻以前的有效量测集，及k时刻的m(k)个有效量测都源于杂波的条件下，可得Z(k)的联合概率密度为

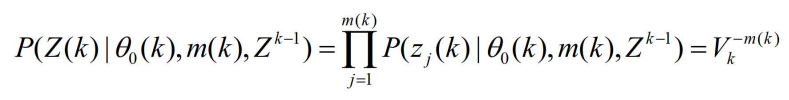
• 对于的任一情形，根据第二个假设，在已知 k 时刻以前的有效量测集，及 k 时刻的 m(k) 个有效量测中有一一个源于目标的条件下，Z(k)的联合概率密度为

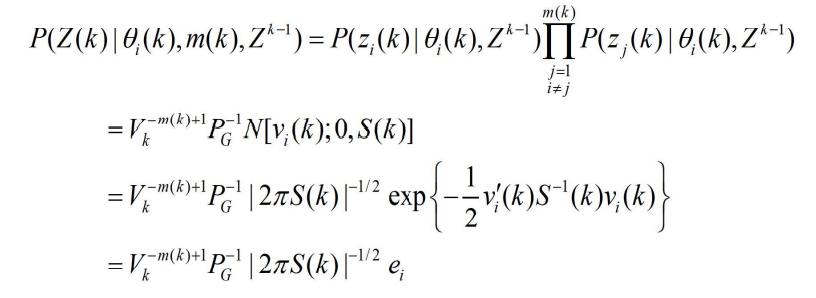
• 其中

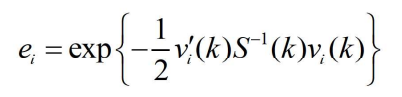
• 将上述三式联立

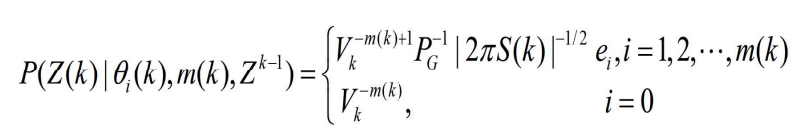
• 带入
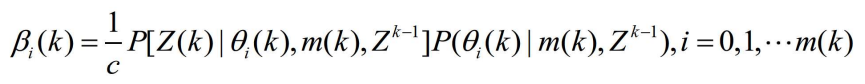
• 得到

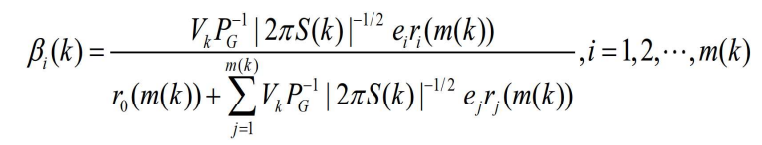
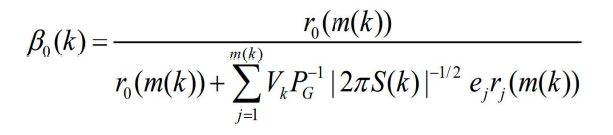
• 其中

4.1.4 协方差P(k|k)的计算

• 和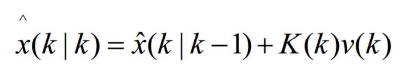相对应的估计地协方差为

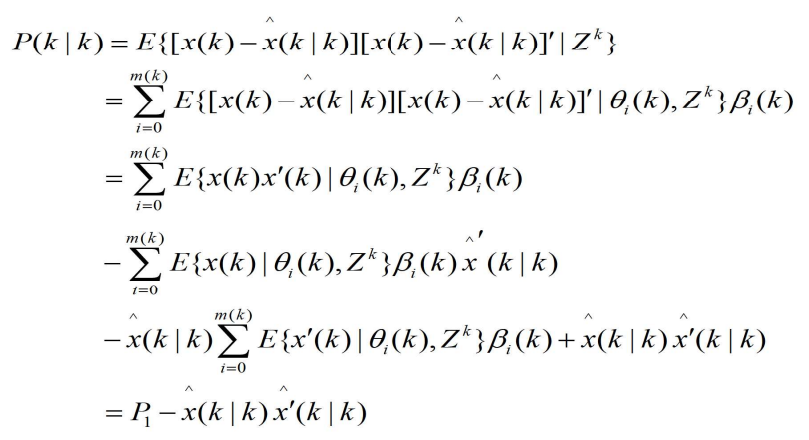
• 其中

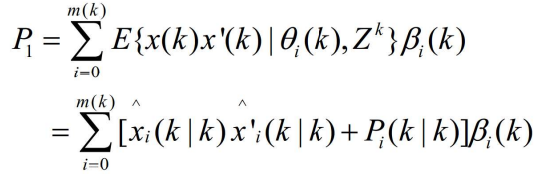
• 其中

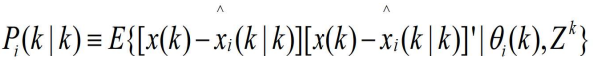
• 如果 i=0，则表示没有量测，此时就是预测的协方差, 即

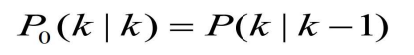
• 若i≠0,则

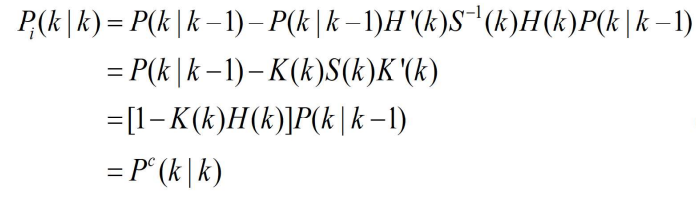
• 将上述两式带入求解P1中

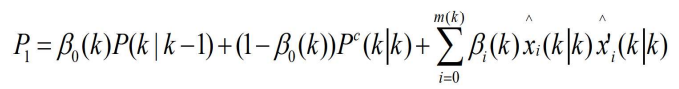
• 再带入求解P(k|k)中

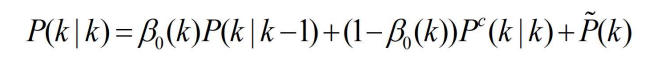
• 其中

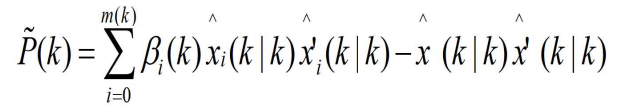
• 将下式代入

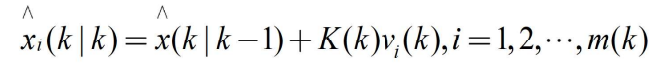
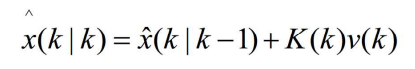
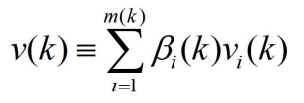
• 得到

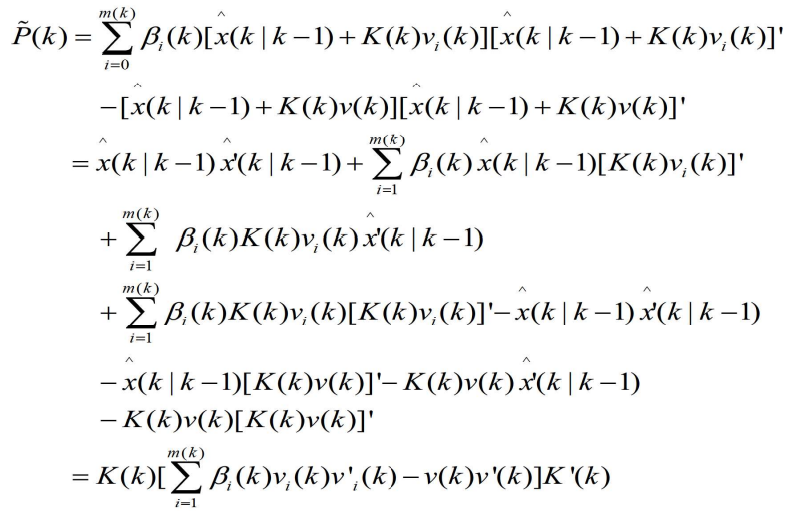
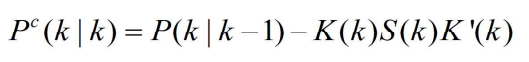
• 将上式带入P(k|k)中