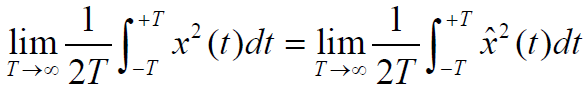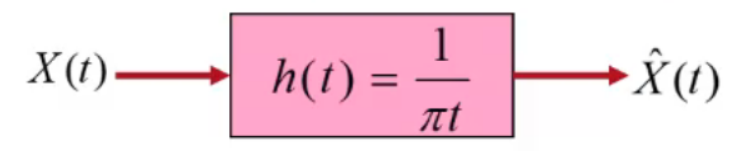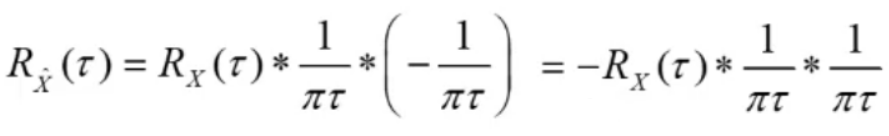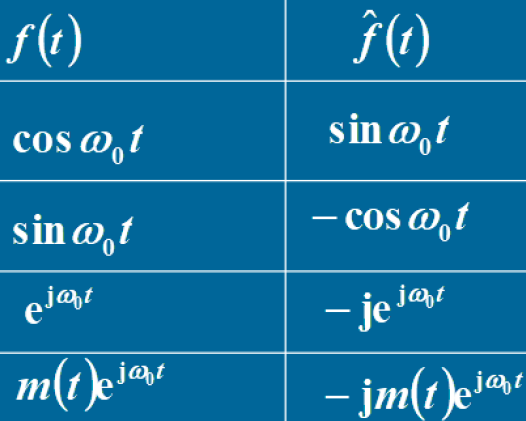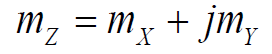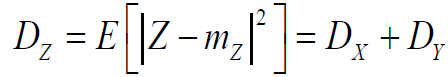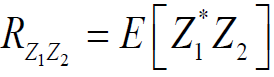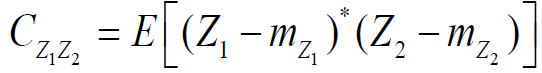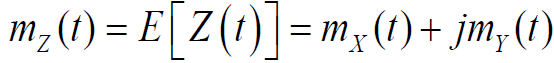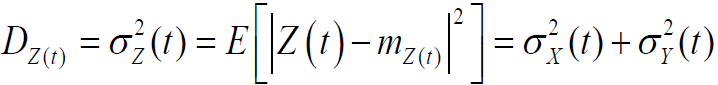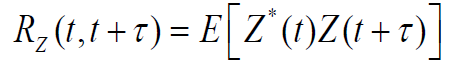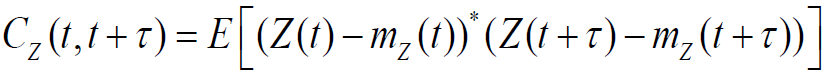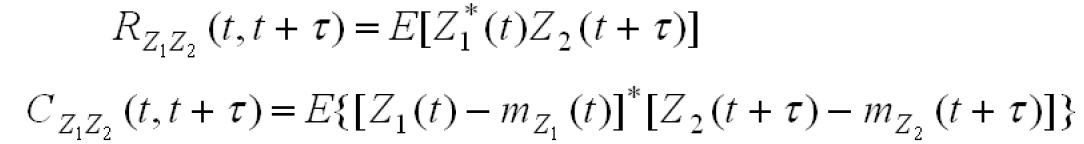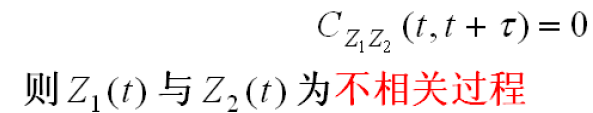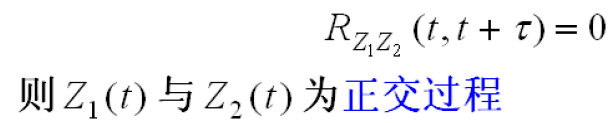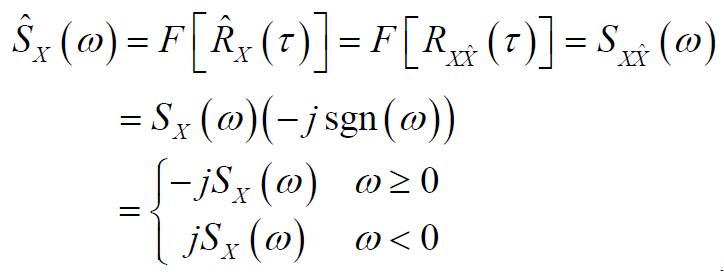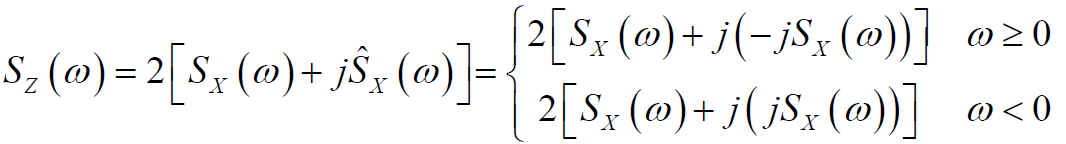1. 希尔伯特变换

• 信号处理的数学工具
• 可以使一个实信号表示成解析信号

• 解析信号：频谱仅在正频率有值的信号

  1.1 解析信号的构成

• 最终目的是使实信号仅在正频谱有值

• 实信号频谱的正负频谱存在关系（复共轭对称性）
• 因此可以用正频谱表示负频谱
• 可得关系

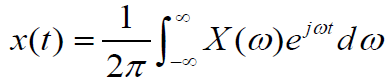
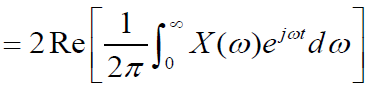
• 即将信号正频谱的2倍的傅氏反变换取实部，等于原信号

• 那么假设原信号为，需要对处理，使其为解析信号

• 的傅氏变换为
• 正频谱的2倍可以表示为
• 做傅氏逆变换为
• 即

• 由的推导可知，解析信号是仅有正频谱分量的复信号

  1.2 希尔伯特变换

  实信号，其希尔伯特变换记为或

• 希尔伯特正变换

• 希尔伯特反变换

• 即存在关系

1.3 实信号复数表示

• 确定性窄带信号表示为

• 令，为低频复包络
• 则窄带信号可以表示为

• 表示为解析信号：
  • 频谱：
• 表示为负指数信号：
  • 频谱：

• 对于窄带信号，其复解析信号和负指数信号是相同的

  1.4 希尔伯特变换的性质

  1.4.1 线性变换

• 希尔伯特变换可以看作是一个冲激响应为的线性时不变网络

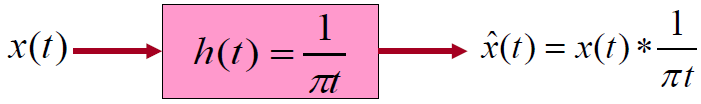
• 对系统函数傅里叶变换得到网络的频率特性

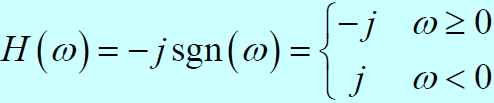
• 幅频特性为：
  • 因此是一个全通滤波器
• 相频特性为：

• 因此是一个90°相移器
• 对信号的正频率部分移相，对信号的负频率部分移相
  

  1.4.2 高阶变换

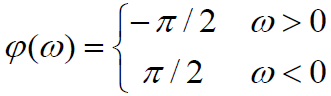
• 偶数阶希尔伯特变换有

• 两次希尔伯特变换的作用相当于一个倒相器

  1.4.3 部分变换

• 

• 

  1.4.4 能量/平均功率不变

• 和的能量相等

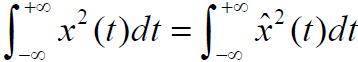
• 和的平均功率相等

1.4.5 自相关函数

• 平稳随机过程与其希尔伯特变换的自相关函数相等（功率谱不变）
• 统计自相关相等

• 时间自相关相等

• 可结合第三章线性系统证明

1.4.6 互相关函数

• 平稳随机过程与其希尔伯特变换的互相关函数等于自相关函数的希尔伯特变换

• 可结合第三章线性系统证明，互相关即为

的中间过程

同理

• 
• 两者的互相关函数是奇函数
• 由于奇函数的过零点特性
• 

• 所以平稳随机过程和在同一时刻正交

  1.4.7 对信号变换

  

  1.4.8 奇偶性

  偶函数的希尔伯特变换是奇函数
  奇函数的希尔伯特变换是偶函数

  1.4.9 周期性

  希尔伯特变换不改变原函数的周期性，不改变域性

  1.5 常用希尔伯特变换对

  

  2. 复随机过程及解析

  2.1 复随机变量

• 

• 

  2.1.1 均值/方差

  
  

  2.1.2 相关矩/协方差

  
  

  2.2 复随机过程

• 

• 

  2.2.1 均值/方差/自相关函数

  
  
  

  2.2.2 协方差函数/互相关函数/互协方差函数

  
  

  2.2.3 不相关过程/正交过程

  
  

  2.2.4 宽平稳复随机过程

• 需要满足三条件

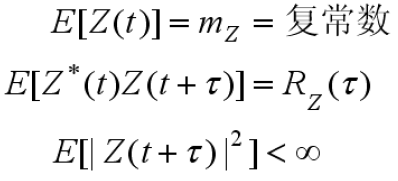
则Z(t)为广义平稳复随机过程
复随机过程的功率谱密度和自相关函数仍然是一对傅里叶变换对

2.2.5 联合平稳复随机过程

• 两个复随机过程各自平稳且联合平稳

两个联合平稳的复随机过程的互功率谱密度和互相关函数仍然是一对傅里叶变换对

2.3 解析过程

2.3.1 解析信号

由实（确定）信号作为实部，其希尔伯特变换作为虚部，构成一复信号

为（复）解析信号

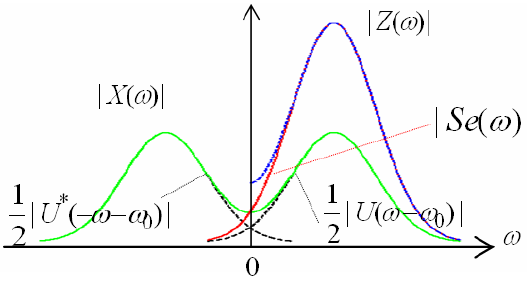
• 解析信号的频谱

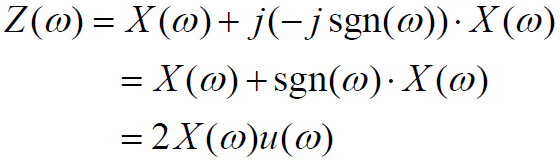
• 希尔伯特变换可以把一个实信号表示成其频谱仅在正频率域的复信号

  2.3.2 解析过程

  由实随机过程作为实部，其希尔伯特变换作为虚部，构成一复随机过程
  
  为（复）解析过程

• 如果为平稳过程，也必为平稳过程（希尔伯特为线性变换过程）

解析过程的数学期望

解析过程的自相关函数

解析过程的功率谱密度

• 对的自相关函数求傅氏变换即可得的功率谱密度

单边功率谱，是正频域谱的4倍
**

2.3.3 解析信号总结

**