便于快速理解，考虑最简单的情况：一维Kalman滤波器

Kalman五方程

一维滤波器仅考虑前后两个过程
当前测量值（输入）为【滤波器】Kalman滤波器 - 图1
当前状态变量（输出）为【滤波器】Kalman滤波器 - 图2
历史状态变量（上一时刻输出）为【滤波器】Kalman滤波器 - 图3

预测状态方程

【滤波器】Kalman滤波器 - 图4
【滤波器】Kalman滤波器 - 图5
【滤波器】Kalman滤波器 - 图6
【滤波器】Kalman滤波器 - 图7
【滤波器】Kalman滤波器 - 图8

预测协方差方程

【滤波器】Kalman滤波器 - 图9
【滤波器】Kalman滤波器 - 图10
【滤波器】Kalman滤波器 - 图11
【滤波器】Kalman滤波器 - 图12
【滤波器】Kalman滤波器 - 图13

卡尔曼增益方程

【滤波器】Kalman滤波器 - 图14
【滤波器】Kalman滤波器 - 图15
【滤波器】Kalman滤波器 - 图16
【滤波器】Kalman滤波器 - 图17
【滤波器】Kalman滤波器 - 图18

更新最优值方程

【滤波器】Kalman滤波器 - 图19
即为输出方程
【滤波器】Kalman滤波器 - 图20
【滤波器】Kalman滤波器 - 图21
【滤波器】Kalman滤波器 - 图22
【滤波器】Kalman滤波器 - 图23
【滤波器】Kalman滤波器 - 图24

更新协方差方程

【滤波器】Kalman滤波器 - 图25
【滤波器】Kalman滤波器 - 图26
【滤波器】Kalman滤波器 - 图27
【滤波器】Kalman滤波器 - 图28
【滤波器】Kalman滤波器 - 图29
【滤波器】Kalman滤波器 - 图30

核心方程的理解

  • 公式经过推导变形后得到最终的五个关键方程，很难从方程中还原物理含义
  • 需要明确方程中各个变量的含义并加以区分
  • 一维为Kalman滤波器最简单的情况，在一维的情况下，各个预测矩阵将退化为单一的数值
  • 简单来说，卡尔曼滤波器是一个最优化自回归数据处理算法，通过协方差的反馈对预测调整
  • 协方差，可以理解为衡量两者相关程度的变量，数值越大，两个变量越相关（相互影响）
  • 可以参考文末其他资料进一步深刻理解：参考资料


仿真测试

matlab代码

  1. %滤波器本体
  2. %输入：当前测量值
  3. %输出：当前状态量（滤波器实际输出）
  4. function Output = Kalmanfilter(zk)
  6. % 输入序列窗口，这里没有实际作用，仅为方便向多维扩展
  7. global x_Array;
  8. global M;
  10. global LastP;    % 上次估算协方差
  11. global Now_P;    % 当前估算协方差
  12. global out;        % 卡尔曼滤波器输出
  13. global Kg;        % 卡尔曼增益
  14. global Q;            % 过程噪声协方差
  15. global R;            % 观测噪声协方差
  17. % 更新选取的x_Array窗口序列
  18. x_cul = x_Array(M);
  19. %x_cul = x_Array(2:M);% 输入序列窗口填充，这里没有实际作用，仅为方便向多维扩展
  20. x_cul(M) = zk;
  21. x_Array = x_cul;
  23. % 上面这一块，在一维情况下等效为
  24. % x_Array = zk;
  26. % 预测状态方程
  27. out=out;
  29. % 预测协方差方程
  30. Now_P=LastP+Q;
  32. % 卡尔曼增益方程
  33. Kg=Now_P/(Now_P+R);
  35. % 更新最优值方程
  36. out=out+Kg*(x_Array-out);
  38. % 更新协方差方程
  39. LastP=(1-Kg)*Now_P;
  41. Output = out;
  43. end

输入测试信号

  • 同LMS自适应滤波器作比较，同样输入混有高斯白噪声干扰的1Hz有用信号，对比观测Kalman滤波器效果
  1. N = 2000;
  2. fs = 200;%(Hz)
  3. t = (0:N-1)/fs;
  4. Freq = (0:N-1)*fs/N;
  6. %有用信号
  7. f1 = 1;%Hz
  8. Input_1 = 5*sin(2*pi*f1*t);
  10. %产生一个高斯白噪声信号
  11. Input_2 = wgn(1,N,2);
  12. Input = Input_1+Input_2;
  14. Input_fft = fft(Input);
  15. %----------滤波器-------------------------------------------------
  16. global LastP;%上次估算协方差 初始化值为0.02
  17. global Now_P;%当前估算协方差 初始化值为0
  18. global out;%卡尔曼滤波器输出 初始化值为0
  19. global Kg;%卡尔曼增益 初始化值为0
  20. global Q;%过程噪声协方差 初始化值为0.001
  21. global R;%观测噪声协方差 初始化值为0.543
  22. LastP = 0.02;
  23. Now_P = 0;
  24. out = 0;
  25. Kg = 0;
  26. Q = 0.005;
  27. R = 0.5;
  29. global M;
  30. global x_Array;
  32. M = 1;                     % 滤波器阶数
  33. x_Array =  zeros(1,M);      % 输入窗口
  35. Output = zeros(1,length(Input));
  37. % 调用滤波器
  38. for N = 1:length(Input)
  39.     Output(N) = Kalmanfilter(Input(N));
  40. end
  42. figure(1);hold on;
  43. plot(t,Input,'r');
  44. plot(t,Output,'b');
  46. %对输出信号做傅里叶变换
  47. Output_fft = fft(Output);
  49. %经过滤波器前后数据频域对比
  50. figure(2);hold on;
  51. plot(Freq,abs(Input_fft),'r');
  52. plot(Freq,abs(Output_fft),'b');

滤波效果

  • 时域上

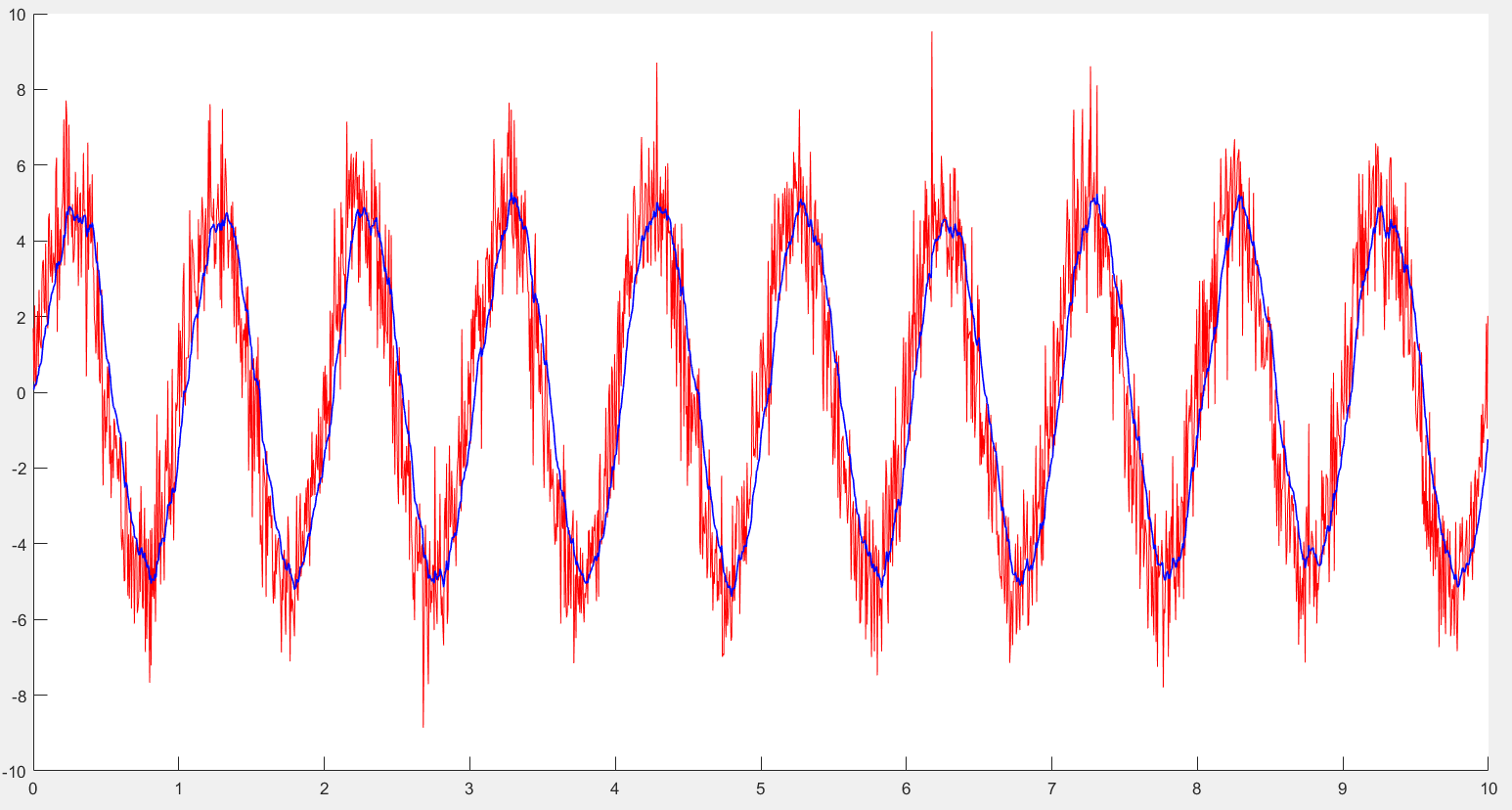
image.png

  1. 红线为混有干扰的1Hz信号波形
  2. 蓝线为经滤波器处理后的信号
  3. 可以看到明显的噪声带来的毛刺得到了抑制
  4. 相较于LMS滤波器的收敛速度更快，波形更稳定
  • 频域上

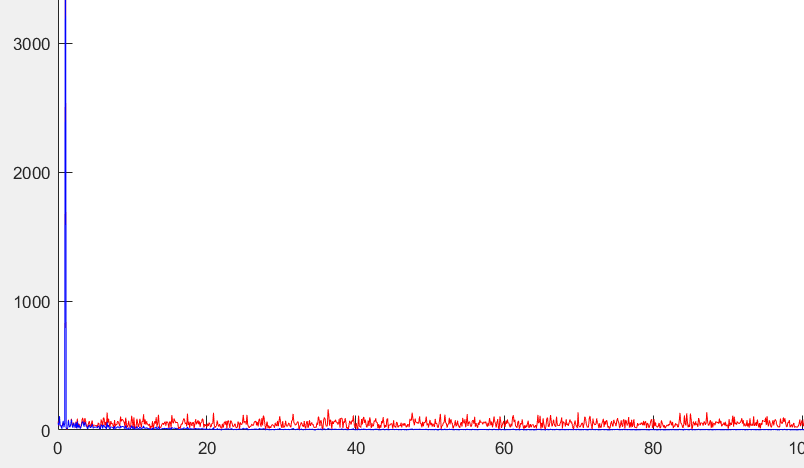
image.png

  1. 频域上也可以看出高频的噪声得到了有效的抑制

性能对比

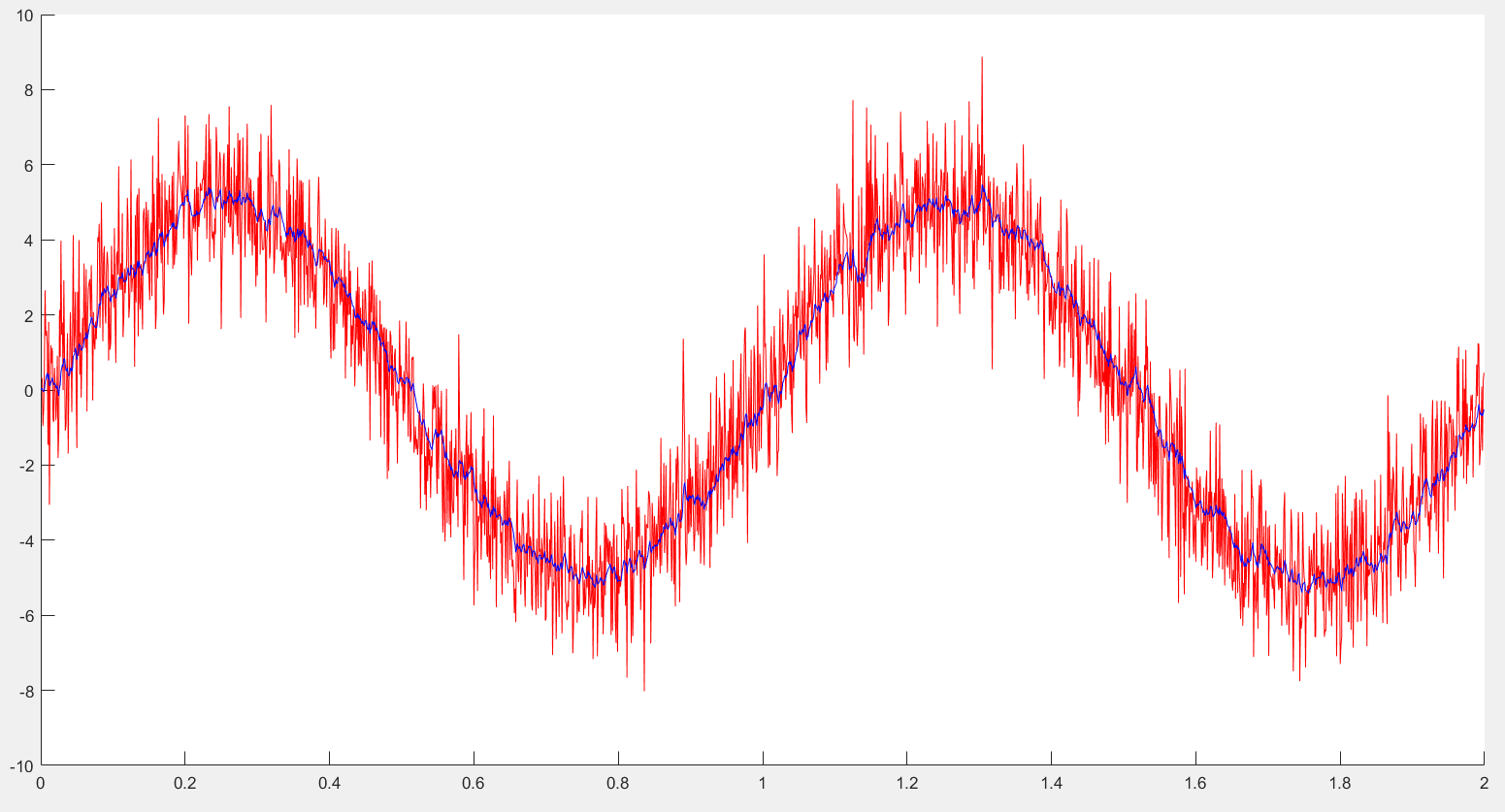
  • Kalman滤波

image.png

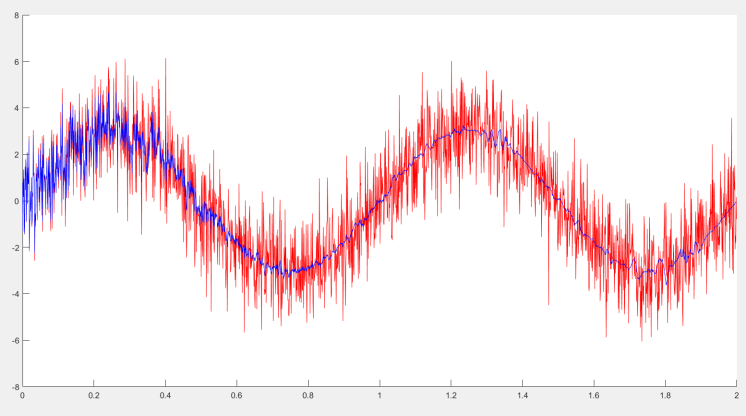
  • LMS滤波

【滤波器】Kalman滤波器 - 图34

  • 通过对比可以得知
  • Kalman滤波器比LMS滤波器的收敛速度更快，LMS需要经历一段时间学习后才可正常工作

  • LMS滤波器正常工作后的波形比Kalman滤波器的输出波形更平滑，更能抵抗突变量的影响

  • 在实际使用中

  • Kalman滤波器的可调参数较多，想要达到理想的滤波效果调试周期较长，而LMS仅需调整阶数和学习率即可

  • Kalman滤波器仅需输入信号即可工作，而LMS滤波器需要纯净的噪声用来学习，条件较难实现

  • 综合来看

  • Kalman滤波器似乎更能适应实际需求

参考资料

  • 通俗理解卡尔曼滤波及其算法实现

https://blog.csdn.net/tiandijun/article/details/72469471

  • 卡尔曼滤波器算法原理以及C语言实现

https://blog.csdn.net/CSDN_X_W/article/details/90289021

  • 卡尔曼滤波的基本原理及应用

卡尔曼滤波的基本原理及应用彭丁聪看图王.pdf