一阶低通滤波器设计

需先阅读文档信号的频域分析

适用场合

低通滤波的目的，保留长期变化，滤掉短暂变化。让信号一点一点的起作用而不是一下子猛烈作用，即在时间范围上取平均。可以滤除一些高频噪声干扰。

抽取模型

由RC低通电路

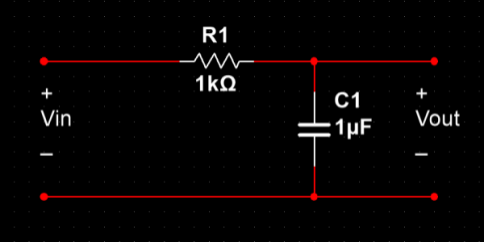
得到Vout与Vin的关系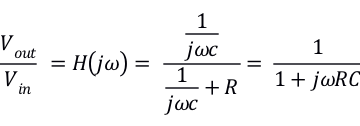

其中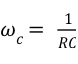

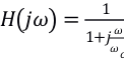
即为电路一阶低通滤波器的数学模型

公式推导

令可得s域的表达式

一阶后向差分法

用一阶后向差分法进行s域到z域的变换

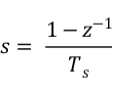
带入并整理可得

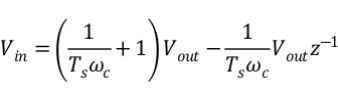
z域到时域变换得到序列关系


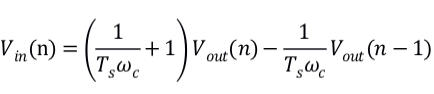
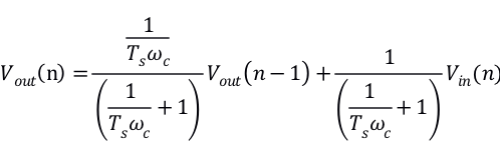
令



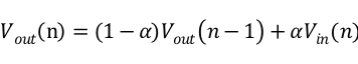
即为数字一阶低通滤波器的计算公式
Ts为采样周期，Wc为截止角频率

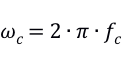
fc为滤波器的截止频率
即可根据所需滤波器的截止频率和采样周期得到公式中的系数α，再依据公式中的序列关系由输入序列得到处理后的输出序列

编程实现

N = 100;                %采样点数
fs = 1000;            %(Hz)采样频率
t = (0:N-1)/fs;    %时间刻度
f1 = 50;                %(Hz)信号1频率
f2 = 300;                %(Hz)信号2频率
f3 = 400;                %(Hz)信号3频率

设想信号1为所需低频信号，信号2，3为高频干扰信号，需要设计滤波器将其过滤
信号时域和频域特征如图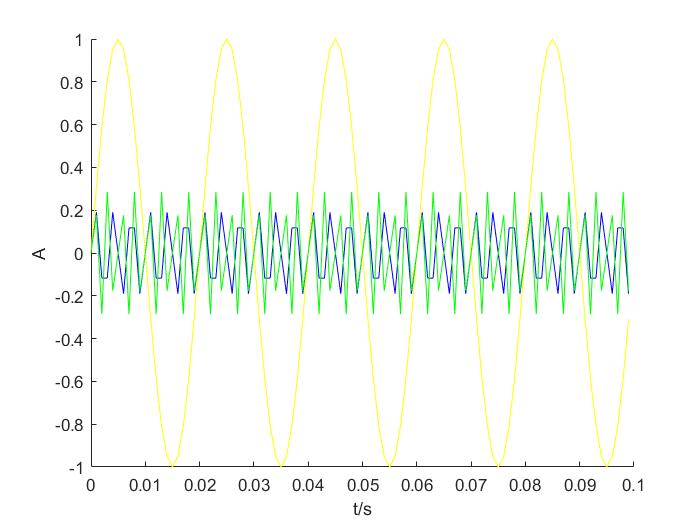

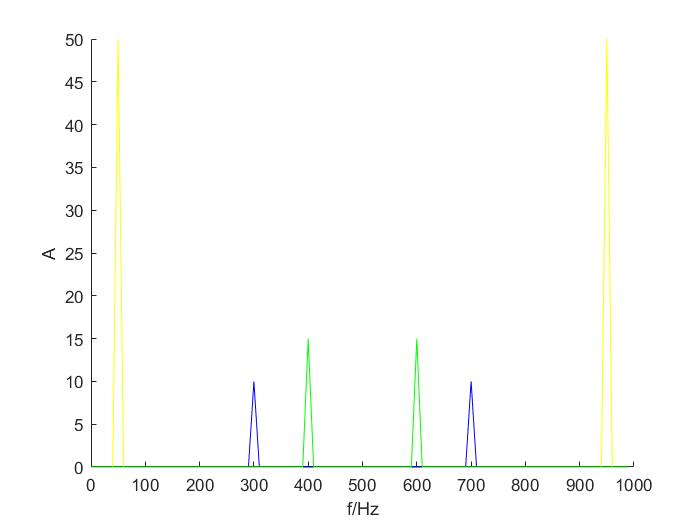
此时多种信号叠加后为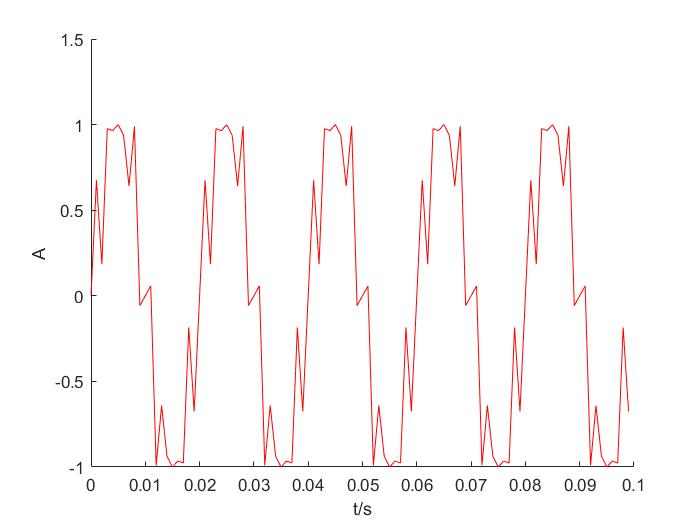

波形较乱，对读取数值造成干扰
从频域上选取滤波器的截止频率为150Hz，由公式计算滤波器系数a

fc = 150;                                    %(Hz)截止频率
a = 1/(1/(Ts*2*pi*fc)+1);    %滤波器系数

滤波器用一函数来实现，将当前采样值和上一历史值作为参数，得到当前输出值

function  Output_filter = Filter_LPF(sample,Output_filter_Last,a)
    Output_filter = Output_filter_Last + (sample - Output_filter_Last) * a;
end

模仿C语言的循环来调用函数以便向单片机移植

Output = zeros(1,length(Input_All));
for N = 1:length(Input_All)
   if(N == 1)
       Output(N) = Filter_LPF(Input_All(N),0,a);
   else
       Output(N) = Filter_LPF(Input_All(N),Output(N-1),a);
   end
end

下图在时域和频域上显示滤波效果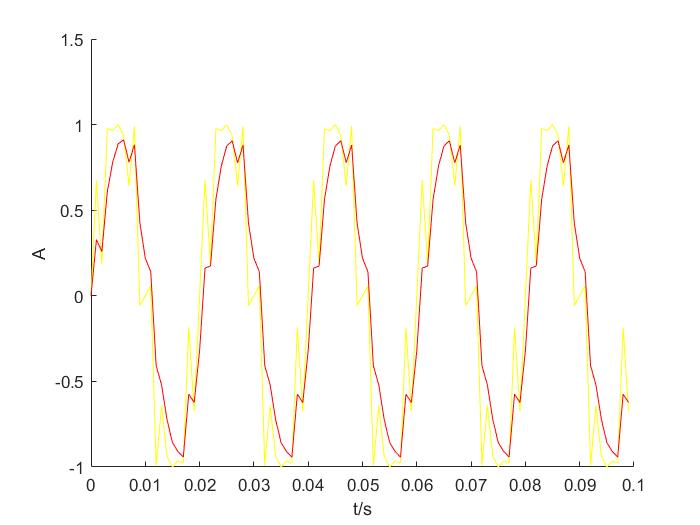

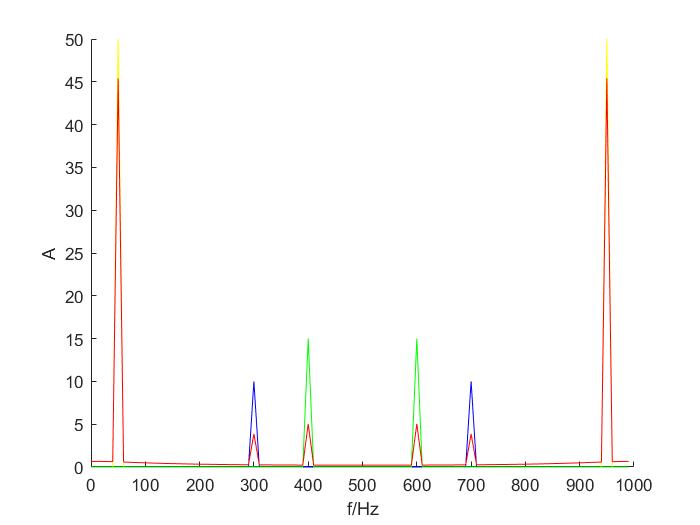
如图，红色线条即为滤波后的波形和频域，滤波后的信号比原来更趋近于正弦信号，高频噪声信号得到了抑制

频域响应

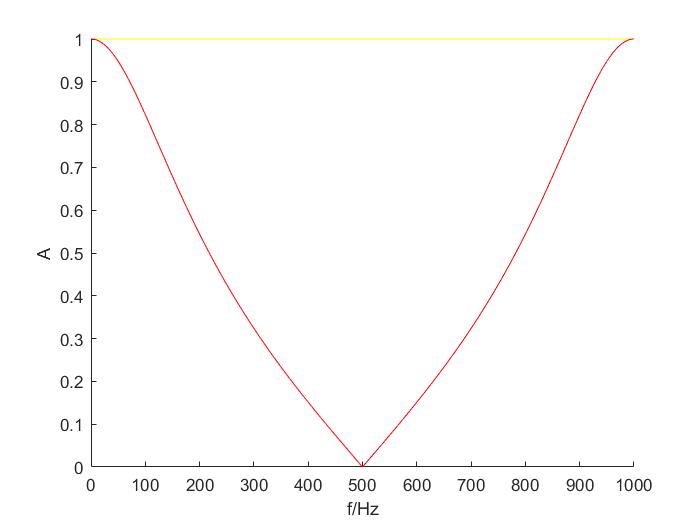
我们将频率低于fs/2（奈奎斯特采样定理）的各种频率的信号通过该滤波器观察它的频域相应得到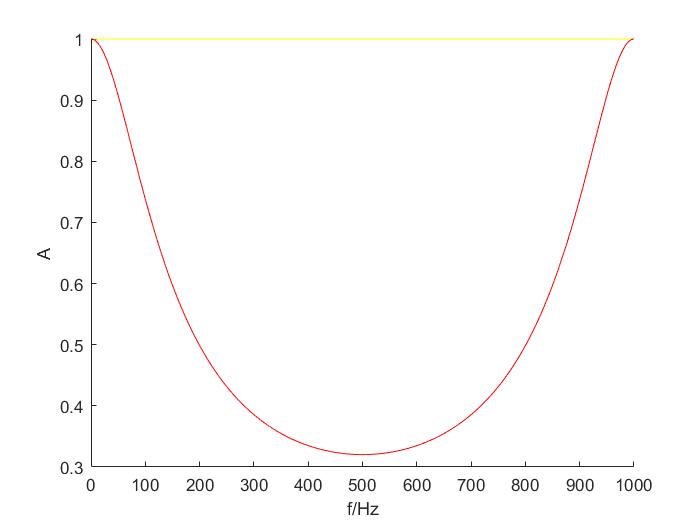

在正频域[0~500]Hz，即满足低通特性，截止频率为150Hz

性能分析

可以从频域响应图中看出，该滤波器在通带的通过性能较好，但是在阻带并不能将信号有效地抑制，在信号的极限处500Hz，抑制比也仅仅只有0.3多，对高频噪声的抑制效果较差。这与很多因素有关，和滤波器的阶数有关，也与s域向z域的变换方式有关，这里采用的一节后向差分法较为粗略，我们换用更为常见的双线性变换法。

程序源码

LPF_1.m
LPF_1N_Response.m

双线性变换法

用双线性变换法进行s域向z域的变换

带入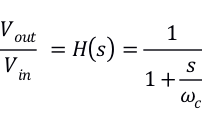

得到

令

整理后得到

再由z域变换到时域得到序列关系

编程实现

function  Output_filter = Filter_LPF(Output_filter_Last,sample,sample_Last)
    global a;
    Output_filter = ((a-1)/(1+a))*Output_filter_Last+(1/(1+a))*sample+(1/(1+a))*sample_Last;
end
global a;
a = 2/(Ts*2*pi*fc);
Output = zeros(1,length(Input));
for N = 1:length(Input)
   if(N == 1)
       Output(N) = Filter_LPF(0,Input(N),0);
   else
       Output(N) = Filter_LPF(Output(N-1),Input(N),Input(N-1));
   end
end

频域响应

性能分析

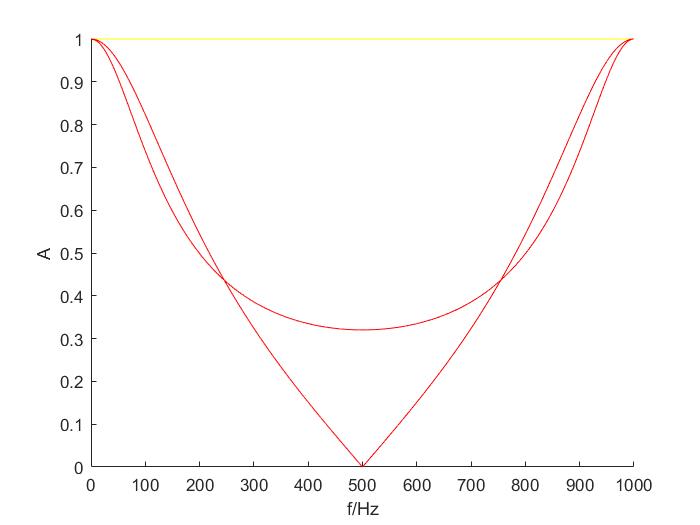
通过对比可以看出，采用双线性变换法设计的滤波器通带和原来差不多，但阻带的抑制效果明显更优

程序源码

LPF_1N_Response.m