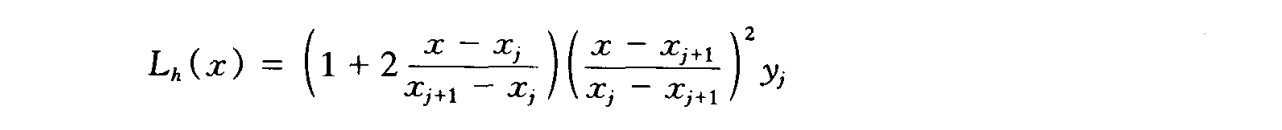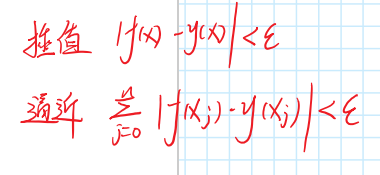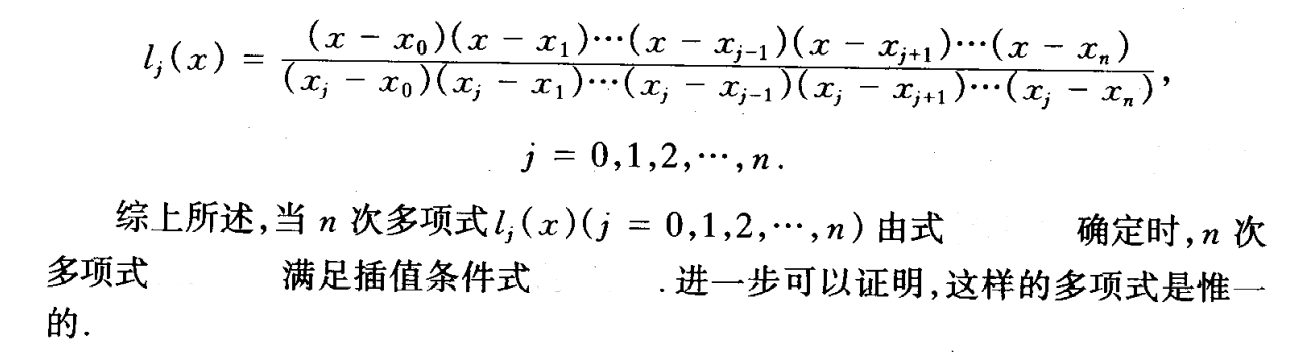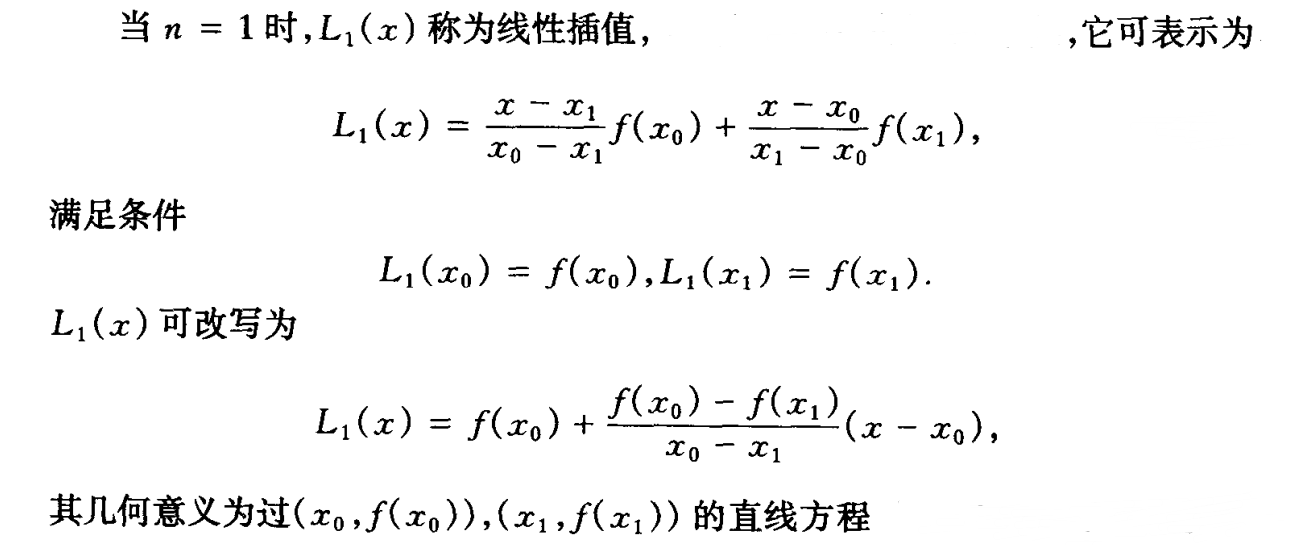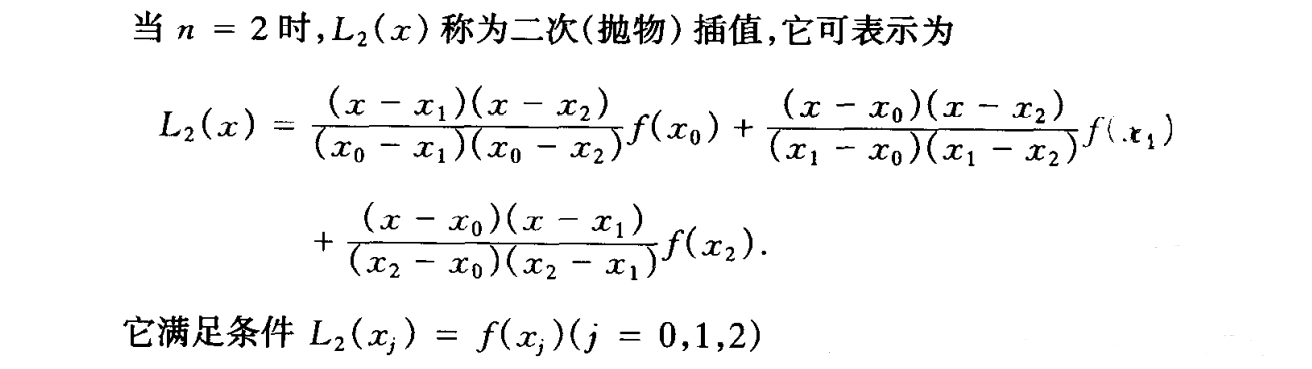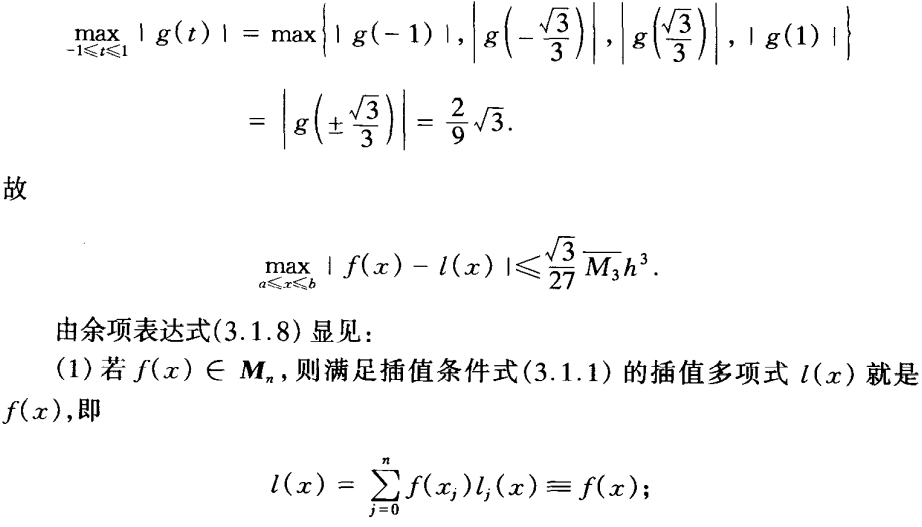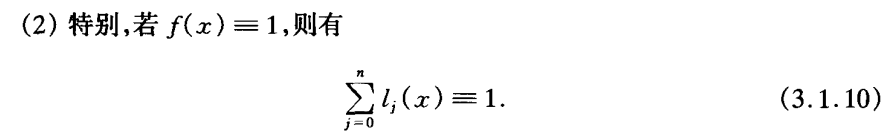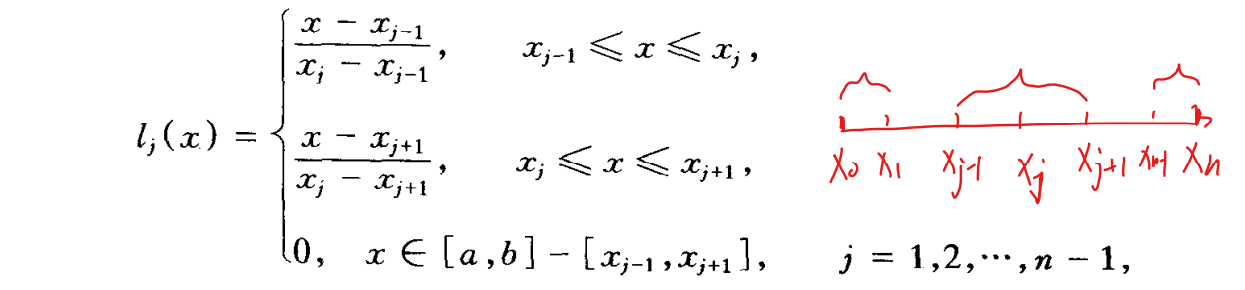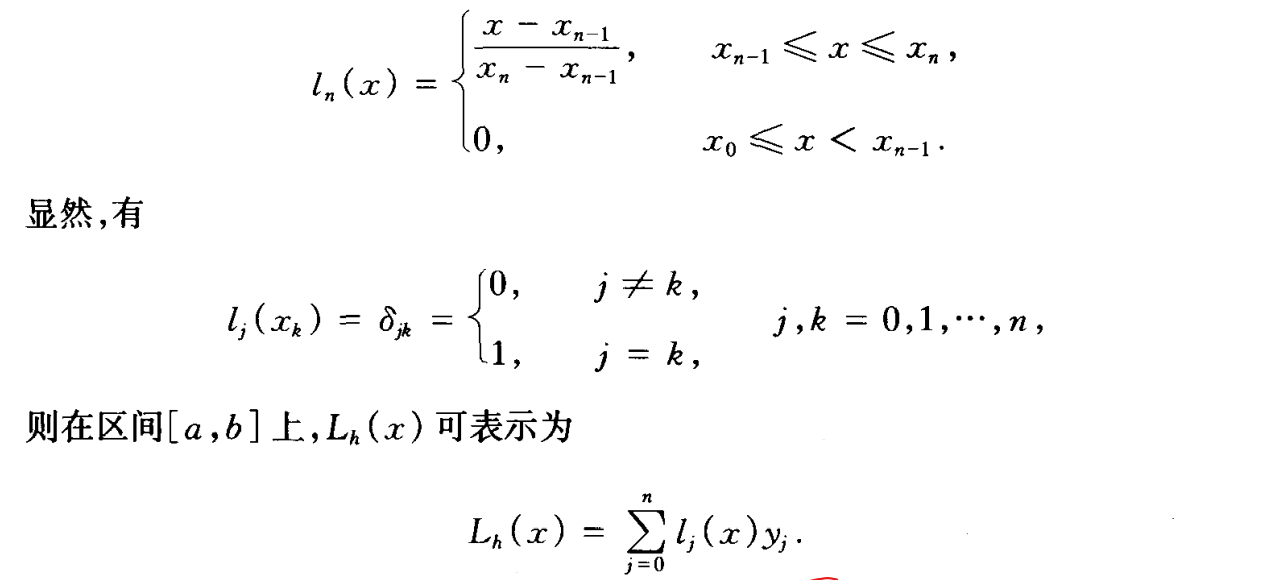• 插值和逼近的区别

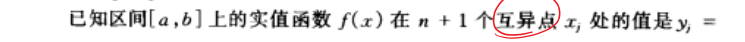
image.png

插值多项式

image.png
image.png

  • 如果直接使用待定系数法求解该多项式

image.png

Lagrange插值

插值公式推导

image.png
image.png
image.png

线性插值

image.png

二次（抛物）插值

image.png

误差检验

  • 插值余项计算

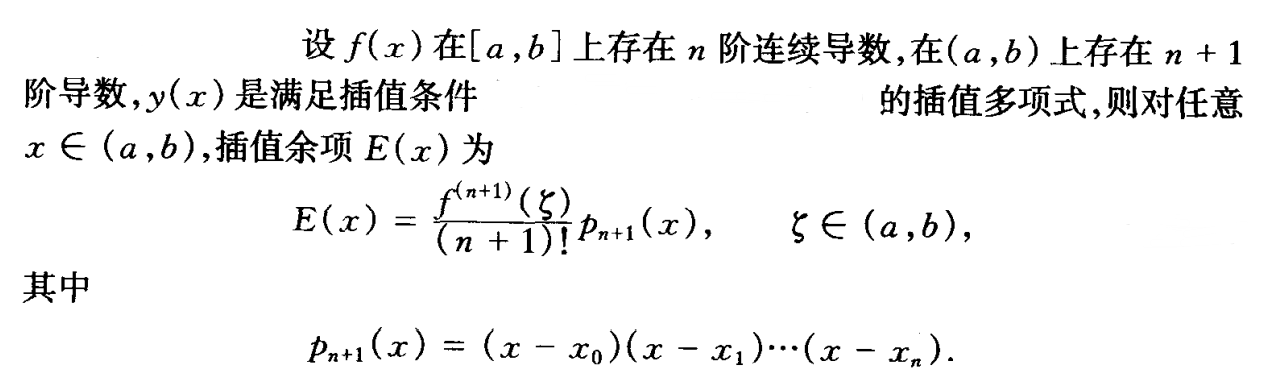
image.png

  • 推导过程

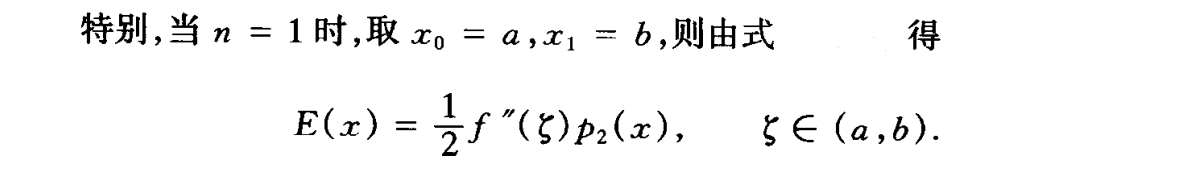
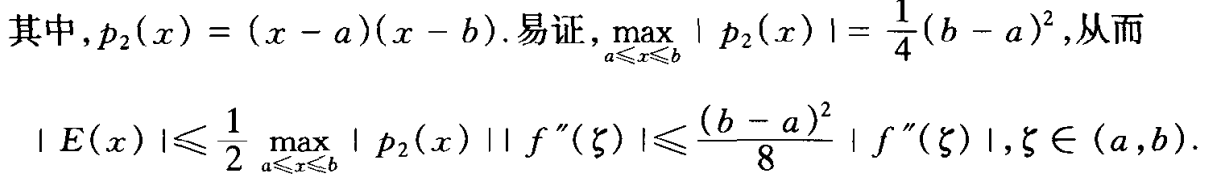
image.png
image.png
image.png
image.png

  • 例题

image.pngimage.pngimage.png

实际应用

image.png
image.png

Newton插值

image.png

差商定义

image.png
image.png

插值余项

image.png
image.png

Hermite插值

image.png

插值公式推导

  • 仿照Lagrange插值多项式构造

【数值分析】多项式插值 - 图26

  • 满足条件

【数值分析】多项式插值 - 图27
【数值分析】多项式插值 - 图28
【数值分析】多项式插值 - 图29
【数值分析】多项式插值 - 图30

  • 已知

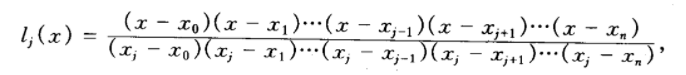
image.png

  • 令

【数值分析】多项式插值 - 图32

  • 同理

【数值分析】多项式插值 - 图33

插值余项

【数值分析】多项式插值 - 图34

  • xj是φ(t)的0点，x也是0点，共n+2个0点，从小到大排列
  • x0,x1,……,xn+1
  • 根据Roll定理
  • φ’(t)=0有n+1个0点，xj也是0点n+1个
  • 再由Roll定理
  • φ’’(t)=0一共有n2个0点
  • …….
  • φ^(2n+2) (t)=0一共有1个0点

【数值分析】多项式插值 - 图35

  • 因此有

【数值分析】多项式插值 - 图36

分段插值

插值公式

  • 在大范围内使用高次插值，逼近的效果往往是不够理想的，故一般不用高次插值而用分段低次插值

image.png
image.png
image.png
image.png

误差分析

image.png

光滑分段

  • 分段三次Hermite插值

image.png
image.png
image.png