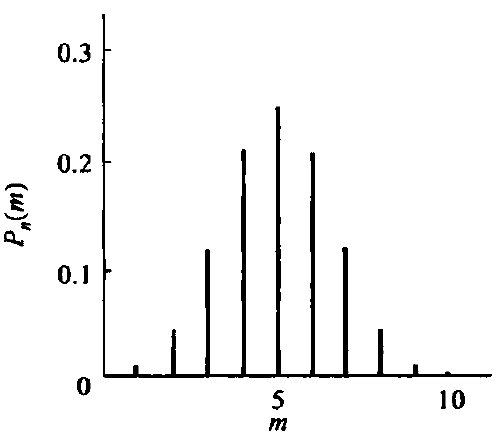
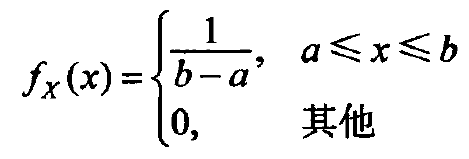二项分布

• n次独立实验，每次实验发生的概率为p，事件A在n次实验中出现m次的概率
• 

• 满足二项分布
• 
• 
• 用来描述离散随机变量
• 二项分布函数是阶梯形式的曲线

• 用于信号检测理论，非参量检测时单词探测的秩值服从二项分布

  泊松分布

• 为试验次数很大，常数时对二项分布的近似

• 

• 在时达到最大值

• 用来描述离散随机变量

  均匀分布

• 

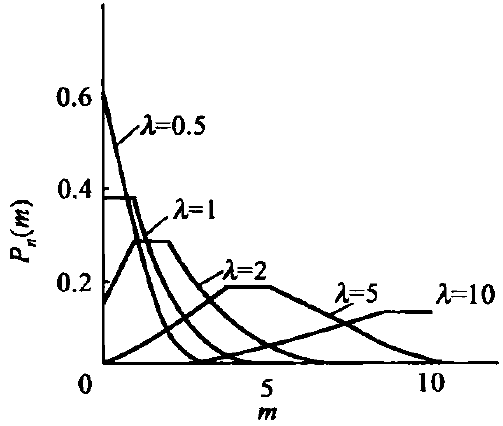
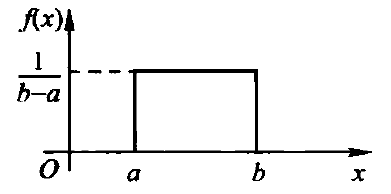
• 常用于数字信号的量化噪声（结尾噪声和舍入噪声）

• 它们的反差相同，不同的是分布的区间，与量化的最小单位有关

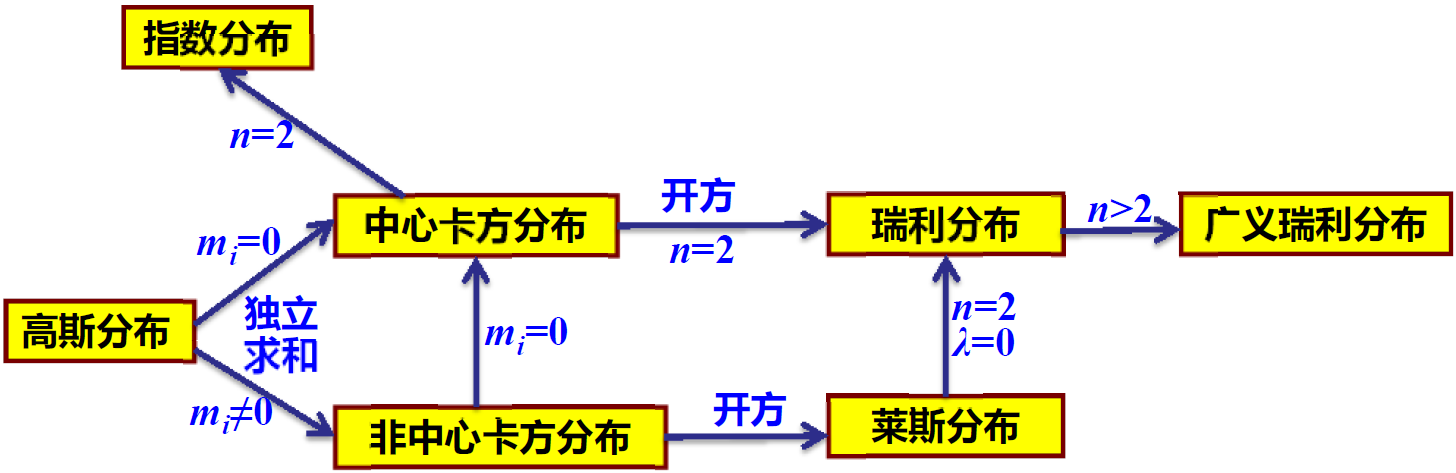
  高斯分布

• 正态分布

• 中心极限定理
  • n个独立随机变量的分布相同，具有有限的数学期望和方差，当n无穷大时，它们之和的分布趋近于高斯分布
  • 即使n个独立随机变量的分布不同，当n无穷大时，如果满足任意一个随机变量都不占优或对和的影响足够小，那么他们之和的分布仍趋于高斯分布

• 特性：不相关的高斯分布一定是相互独立的（宏观体现了微观），仅高斯分布具有该特性

  χ²分布

• 窄带信号，包络检波

• 小信号检波，平方律检波，检波器输出的是信号与噪声包络（高斯分布）的平方
• 检测错误减小，对检波器输出信号积累

• 积累的次数 为χ²分布的自由度

  中心χ²分布

• 方差相同的积累的高斯分布的数学期望为0

• n=2，两个自由度的中心χ²分布为指数分布

• 两个χ²分布之和仍为χ²分布，自由度为其和

  非中心χ²分布

• 积累的高斯分布的数学期望不为0（可看作是期望为0的高斯变量与确定信号之和）

• 两个非中心χ²分布之和仍为非中心χ²分布，自由度为其和，非中心χ²分布参量 也为其和

  瑞利分布

• 自由度为2的中心χ²分布开方所得

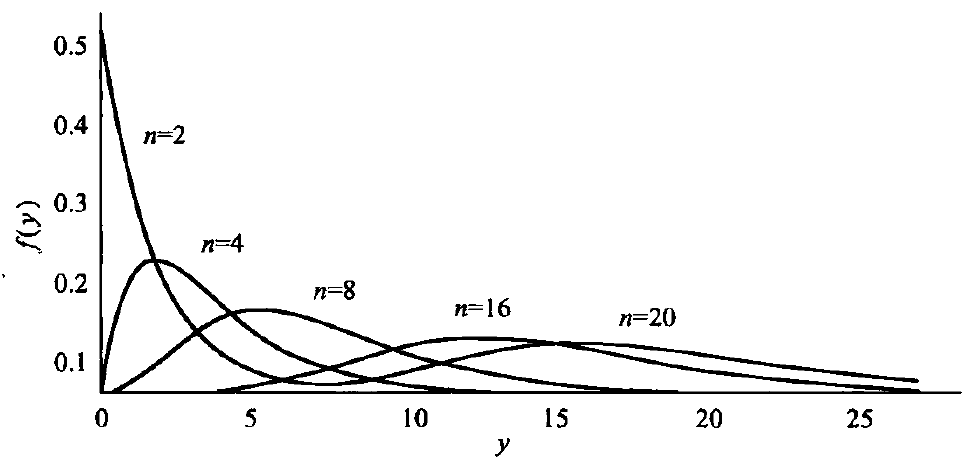
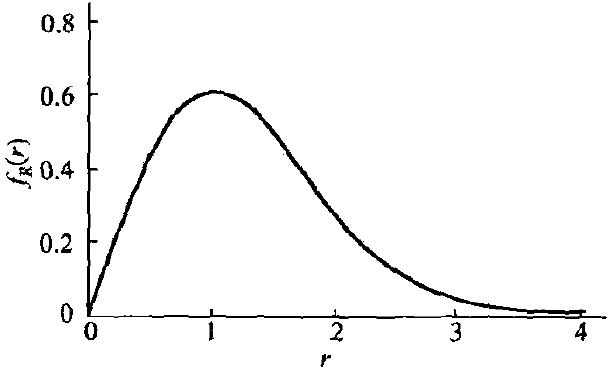
• 瑞利分布的数学期望与原高斯变量的均方差成正比

• 因此当需要估计高斯变量的方差（功率）时，往往通过估计瑞利分布的数学期望得到（期望比方差更易得）

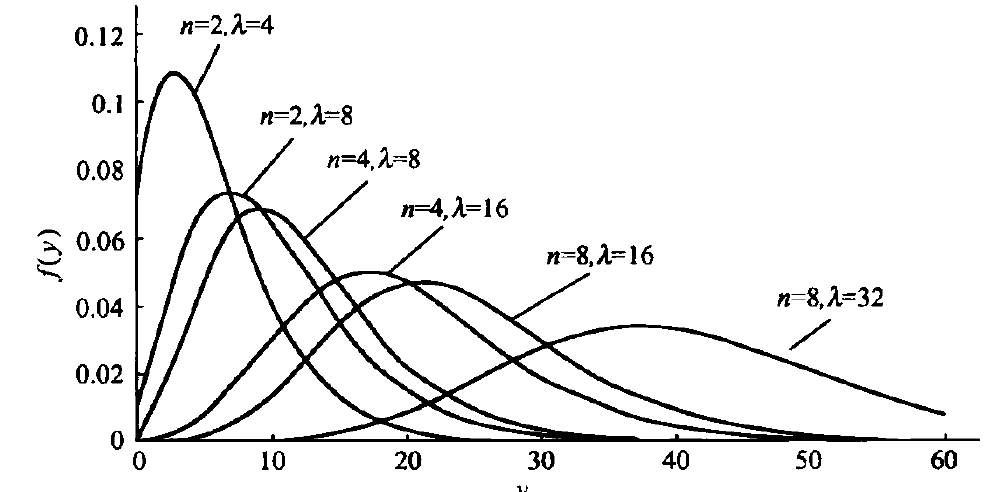
  广义瑞利分布

• 自由度为 的中心χ²分布开方所得

  莱斯分布

  自由度为 的非中心χ²分布开方所得

• 瑞利分布是莱斯分布中非中心χ²分布参量 = 0的特例

分布在通信原理的体现

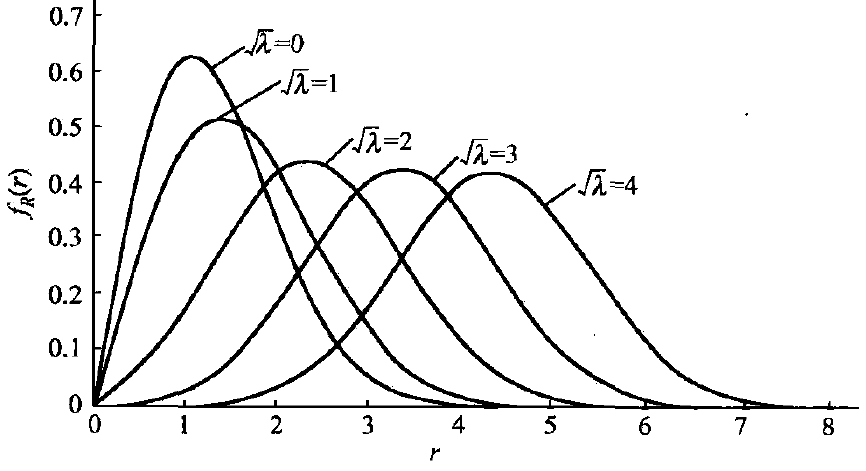
正弦信号加窄带高斯信号（信号加噪声）的合成波包络分布与信噪比有关
小信噪比时，它接近于瑞利分布
大信噪比时，它接近于高斯分布
在一般情况下它是莱斯分布（广义瑞利分布）

正弦信号加窄带高斯噪声（信号加噪声）的随机相位分布与信噪比有关
小信噪比时，相位分布接近于均匀分布，它反映这时窄带高斯噪声为主的情况
大信噪比时，相位分布主要集中在有用信号相位附近