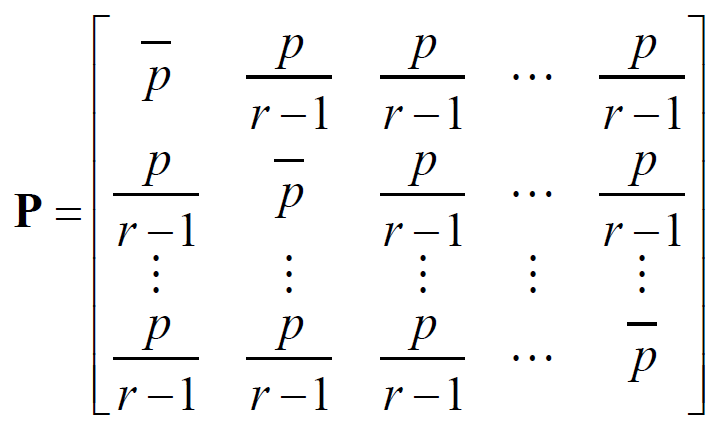1. 离散单符号信道

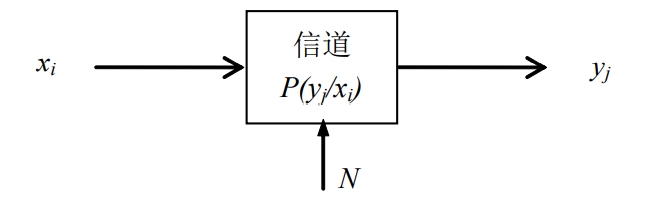
1.1 信道模型

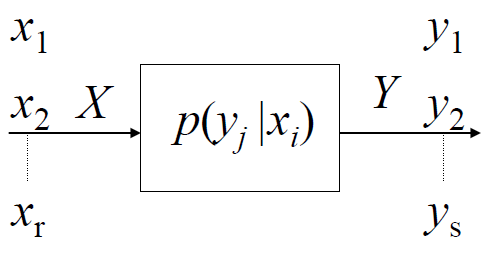
先验概率：
前向概率（信道传递概率）：
输出符号概率：

后验概率：

注：由的矩阵运算可知
矩阵即为将的每一行与的每一列对应项相乘（先不相加）可得
为在其每一列的和（即）的比例

1.2 信道疑义度

表示接收端收到信道输出的一个符号后对信道输入的符号仍然存在的平均不确定性

• 理想信道(无噪声信道)：
• 一般情况
• 当，表示信道未发挥作用，通信未建立

注：不可直接用矩阵计算，同理不可直接用矩阵计算
由矩阵仅可以得到，而计算需要用到，因此还需要结合矩阵才可计算

1.3 平均互信息

• 对于单个符号的信息量存在关系

• 对于给定离散信道[P(Y/X)]，接收端接收到随机变量Y的任一符号后
• 获取关于信源随机变量X的任一符号平均信息量

• 接收者收到的信息量=信源熵-信道疑义度

• 平均互信息量的交互性

• 平均互信息量给出了信道传输一个信源符号所传递的平均信息量，对于给定的信道和信源，平均互信息量是一个确定的量。两个随机变量之间信息传递能力的描述.

• 凸函数和Jensen不等式

• 数学结论
  • 如果 f 是上凸函数，则变量均值的函数大于等于函数的均值
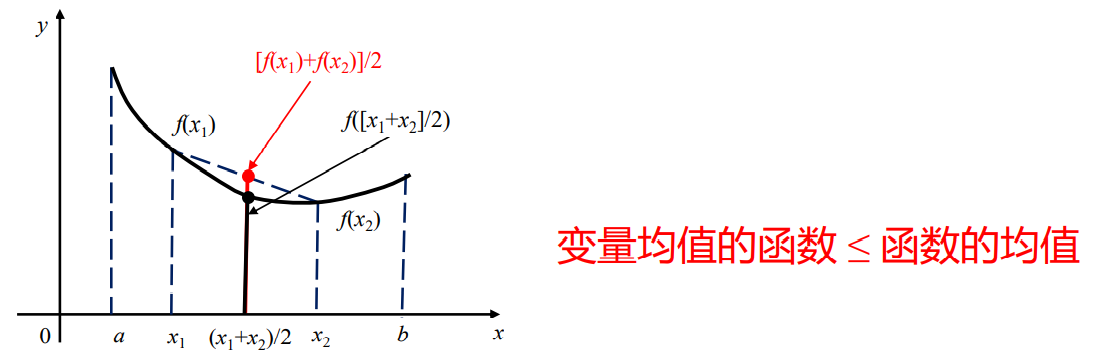
  • 如果 f 是下凸函数，则变量均值的函数小于等于函数的均值
  • 可以证明底大于1的对数函数是严格上凸函数
• 凸集合
  • 如果和是n维向量空间R中的任意两个n维向量，对于，有 ，则称R为一个凸集合
  • 从几何关系上看，α和β是集合R中的任意两点， 表示连接这两点的连线也属于这个集合中。图给出了凸集合与非凸集合的示意图。

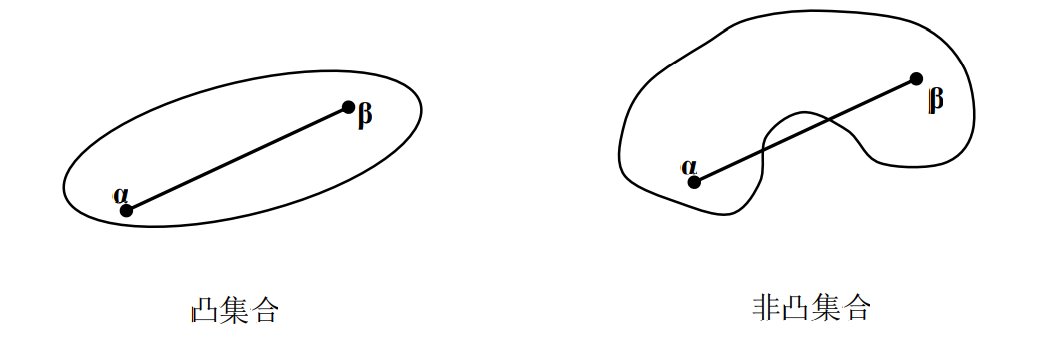
• Jensen不等式
  • 假设f(x)在区间(a,b)上是一个严格上凸函数，也就是意味着对于x1,x2∈(a,b)，以及参数θ=1/2，有关系：

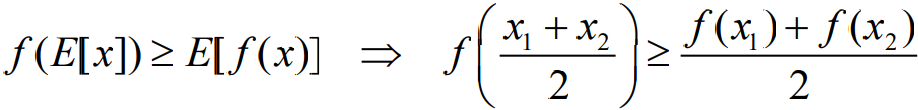
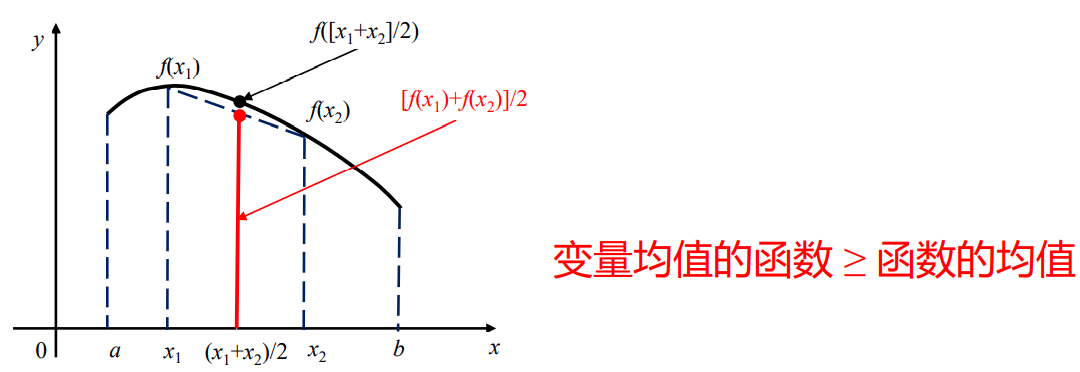
• 假设f(x)在区间(a,b)上是一个严格下凸函数，也就是意味着对于x1,x2∈(a,b)，以及参数θ=1/2，有关系：

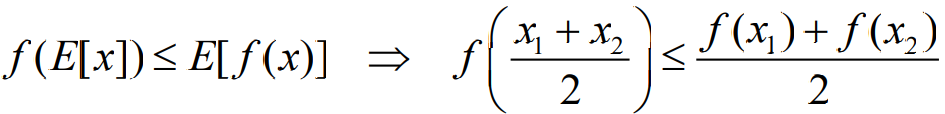
• 利用Jensen不等式证明最大熵定理

• 利用Jensen不等式证明互信息量的非负性

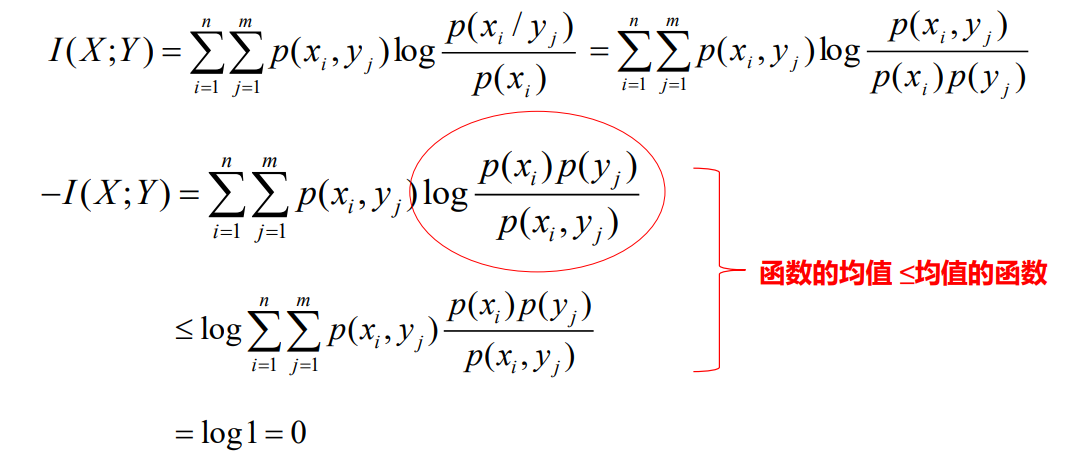
• 在一个离散无记忆信道的通信系统中，只要信宿的随机变量Y与信源X具有一定的相关性，从统计上讲就一定能够从Y中得到关于X的信息量。只有当X与Y相互独立，交互信息量才等于零。

• 交互信息量的非负性说明，后验熵不可能大于先验熵，噪声熵不可能大于信宿熵，联合熵也不可能大于独立熵之和。实际上，这一点可以很容易地推广为条件小于等于无条件熵，联合熵小于等于独立熵之和。

• 平均互信息量的凸函数性

• 平均交互信息量描述了一个信源符号经过信道后，信宿可以获得的信息量，平均信息量完全可以用信源和信道的统计特性来描述

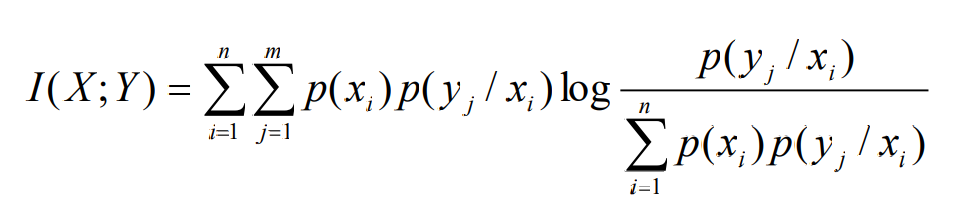
• 这个表达式表明，平均交互信息量是信源先验概率p(xi)和信道转移概率p(yj/xi)的函数。
• 如果信道固定，I(X;Y)就是信源先验概率的函数，

• 如果信源固定，I(X;Y)就是信道转移概率的函数。

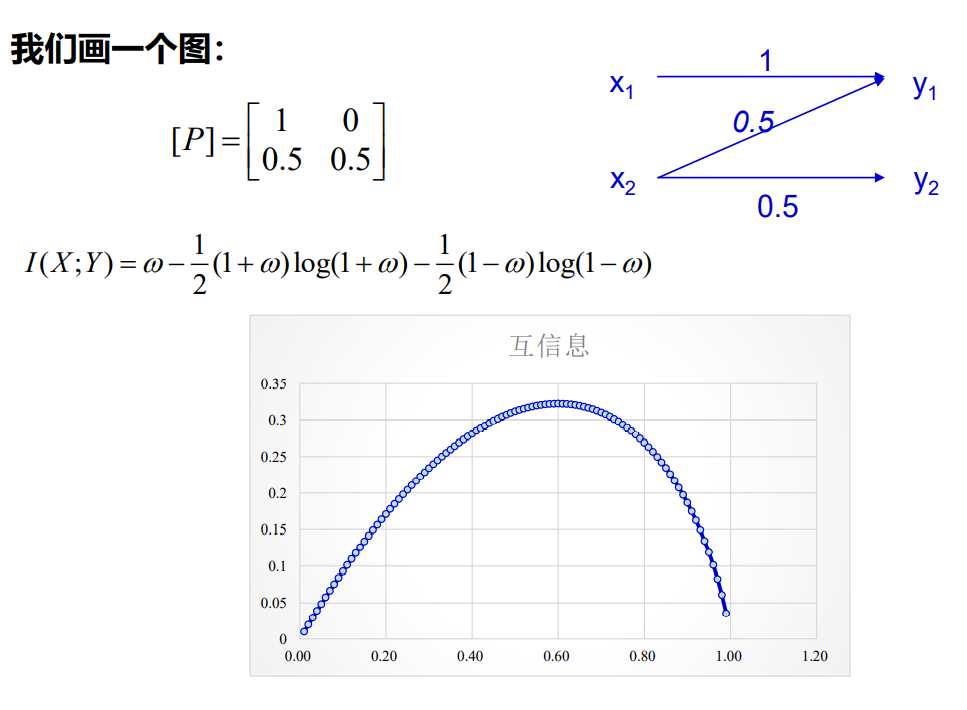
• 对于固定信道，平均互信息是信源概率分布的上凸函数

  • 即存在一种信源分布使平均互信息最大，最大值由信道本身决定
• 对于固定信源，平均互信息是信道转移概率的下凸函数
  • 即存在一个最差信道（二元对称信道：转移概率为1/2时）使信道的干扰最大

1.4 信道容量

• 信息传输率，信道中平均每个符号所传送的个信息量
  • bit/符号
• 信息传输速率，信道每秒钟平均传输的信息量
  • bit/s

存在信源概率分布使信息传输率达到最大

信道容量定义：信息传输率最大值

相应的输入概率分布被称为最佳输入分布

• 信道容量的大小与此时采用的信源概率分布无关，仅由理想信源分布决定,它是一个极值性质,
  仅由信道矩阵即可求出,达到信道容量时信源分布和信道容量的大小
• 是信道能够传输的最大信息量
• 是完全描述信道特性的参量

计算信道容量与计算的过程一致
此时可将称为噪声熵

1.5 特殊信道

• 有噪信道
  • 输出符号个数比输入符号个数多
  • 有扩展性能
• 无噪信道
  • 输出符号个数少于或等于输入符号个数
  • 有归并性能
• 有损信道
  • 输入与输出不是确定的对应关系,概率空间存在重叠,即可能两个不同的输入产生相同的输出
• 无损信道
  • 输入与输出的概率空间不重叠,两个不同的输入不会产生相同的输出

    1.5.1 有噪无损信道

    一个输入对应多个输入(扩展性能),但从输入总能找到唯一对应的输入
    此时信道疑义度（损失熵）为0
    此时H(X)信道容量为输入等概率分布时的平均互信息量

1.5.2 无噪有损信道

输入符号多于输出符号时,必定有损,此时存在多个输入对应一个输出的情况
此时噪声熵为0
此时H(X)＞H(Y)
信道容量为输出等概率分布时的平均互信息量

1.5.3 无噪无损信道

输入与输出之间确定的一一对应关系
此时噪声熵和损失熵均为0
H(X)=H(Y)
输入等概分布时，输出也等概分布，平均互信息量达到信道容量

1.5.4 相互关系

有噪无噪针对的是噪声熵，即
有损无损针对的是信道疑义度，即
噪声熵是X转移为Y的不确定性造成的
损失熵（信道疑义度）是Y解释为X的不确定性造成的

1.6 信道容量

1.6.0 熵速率与信道容量

• 单位时间内传递的平均信息量为熵速率。当符号速率为r符号/秒时，单符号离散无记忆信道模型的熵速率为

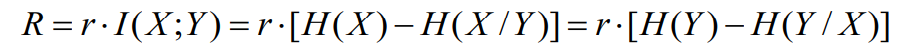
• 在信息论中，定义熵速率及信道容量的目的是研究通信能力与信源和信道统计特性的关系，因此，参数r并没有多大理论意义，通常假定r=1，可表示为

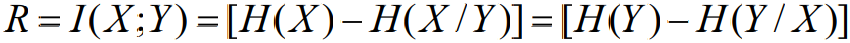
• 从数学模型化的角度看，熵速率就是互信息量。
• 熵速率既是信源先验概率的函数，也是信道转移概率（统计特性）的函数
• 为了专门描述某一个信道的统计特性对通信系统信息传输能力的影响，信息论又定义了信道容量
• 信道容量是在给定信道条件下（即一定的信道转移概率），对于所有可能的信源先验概率分布的最大熵速率

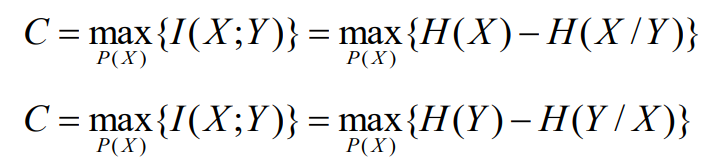
• 根据互信息量的性质我们知道，对于给定的信道转移概率，互信息量是信源先验概率的上凸函数，因此存在一种先验概率分布使互信息量达到最大值，这个最大值就是信道容量。
• 根据信道容量的定义可以看到，信道容量与信源无关，它只是信道转移概率的函数，不同的信道就有不同的信道容量，它反映了信道本身的传信能力。

  1.6.1 行对称信道

  每行都是第一行的排列
  

因为行对称信道，每取一个，后面的项相等，因此该式也可写为

因此对于行对称信道，仅有信道矩阵即可描述噪声熵，且仅有一行数值即可计算得出

1.6.2 对称信道

列与行同时满足对称要求

1.6.3 准对称信道

自身不是对称信道，但其子阵是对称信道

1.6.4 强对称信道

信道矩阵为对角阵，形如

1.6.5 不同信道的信道容量

即仅通过信道矩阵计算信道容量,和达到信道容量时对应的信源分布

• 对称信道
• 对称信道，信道的输入概率分布为等概分布时，输出分布必定也等概
• 对称信道，当输入等概分布时，达到以下信道容量

• 一般行对称信道
• 一般离散行对称信道，不一定存在一种输入分布使输出等概率

• 准对称信道
• 离散准对称信道，当信道输入概率分布为等概的情况下达到信道容量

• 注意这里第一项是输入等概分布的信源熵
• 该准对称信道可以划分为 个子阵（对称信道），为第k个子阵的任意一行行元素之和，为k个子阵的任意一列列元素之和
  • 一般信道
  • 推导过程
• 信道容量：给定信道条件下，互信息量关于信源先验概率的最大值

• 利用拉格朗日乘数法，构造一个关于先验概率的辅助函数

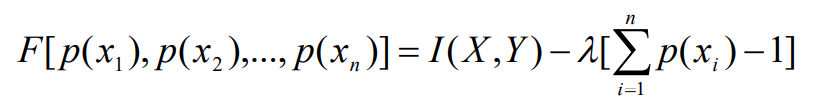
• 其中的λ为待定系数，对辅助函数求关于概率分布p(xi)的导数，并使其为0，得到n个方程构成的方程组：

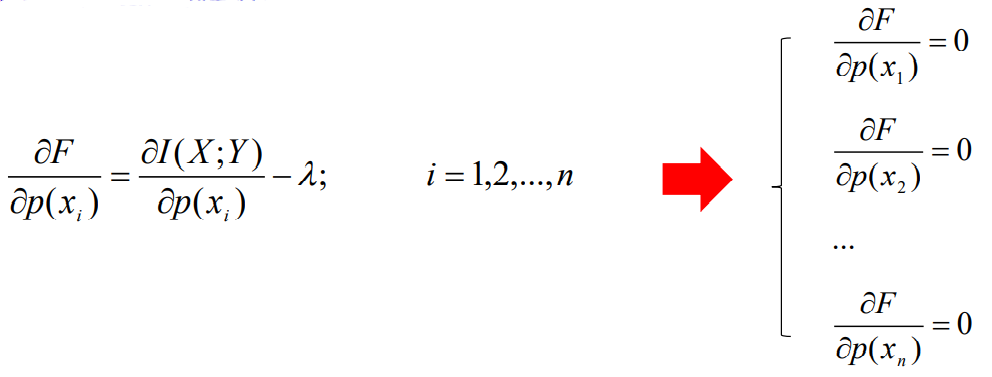
• 利用互信息量关系（以e为底计算更方便)

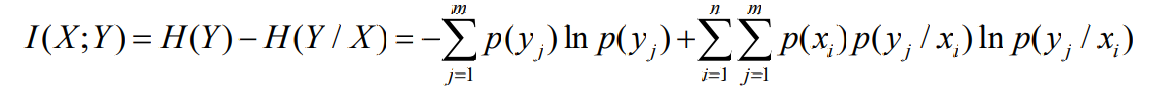
• 得到方程组：

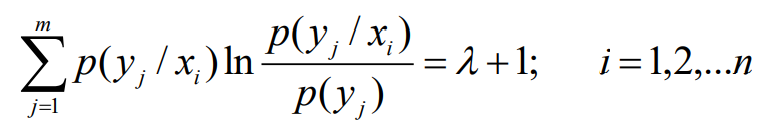
• n个方程加上约束方程共n+1个方程，求n+1个未知数，解这个方程组就可以求出获得信道容量时的信源先验概率分布。
  • 计算过程
• 转化为求对信源概率分布的条件极值
• 计算过程
  • 列举方程
  • 由,可得,可以求出信道容量
  • 同时由上式可以求得
  • 再结合信道矩阵即可求得信源分布
• 对于二元分布,即信道转移矩阵为2×n阶时,可以设二元概率分布,然后直接对求导
  • 注:对于同一矩阵可以有不同的求解方法得到相同的结果
  • 例题

1.7 信道容量定理

达到信道容量的充要条件是输入分布满足以下充要条件:

2. 离散多符号信道

2.1 信道模型

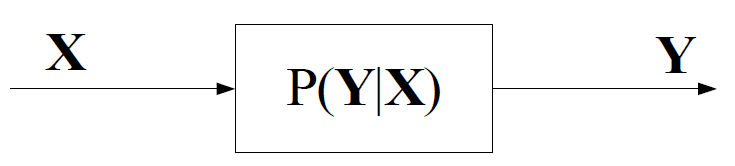
输入输出随机序列的长度为N的离散无记忆平稳信道，为离散无记忆信道的N次扩展信道\

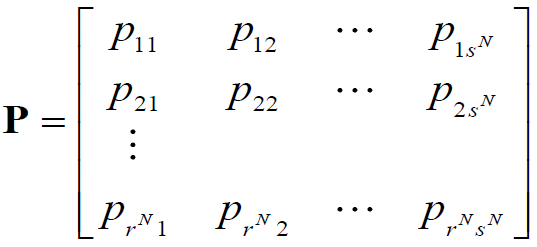
次扩展，每个信源符号有种可能，即信源有种可能的组合
次扩展，每个输出符号有种可能，即信源有种可能的组合

2.2 离散无记忆信道

信道在任意时刻的输出只与此时刻信道的输入有关，而与其他时刻的输入输出无关，则为离散无记忆信道（DMC）
则满足

即状态转移概率就等于组成状态的各个符号的符号转移概率的乘积

• 多符号互信息量与单符号互信息量之间的关系

若信道的输入和输出分别是长序列和，且信道是无记忆的，则

即多符号互信息量小于等于单符号互信息量相加
当信源也是无记忆信源时等号成立

• 信源和信道均无记忆时

N次扩展信道，信源和信道均无记忆时，若输入序列中每一个随机变量均取自同一信源符号集且具有同一种概率分布时，通过相同的信道后，输出序列中的每一个随机变量也取自同一符号集，且具有相同的概率分布

且满足关系

2.3 离散多符号信道的信道容量

输入、输出序列长为N的离散无记忆信道

当信源也无记忆时，且输入序列每一个随机变量达到最佳输入概率分布时

3. 组合信道

3.1 独立并联信道

• 离散多符号无记忆信道即可视为多个独立单符号信道的组合
• 与离散多符号无记忆信道公式一致
• 
• 

• 

  3.2 级联信道

• 级联信道的总的信道矩阵等于这两个串联信道的信道矩阵的乘积

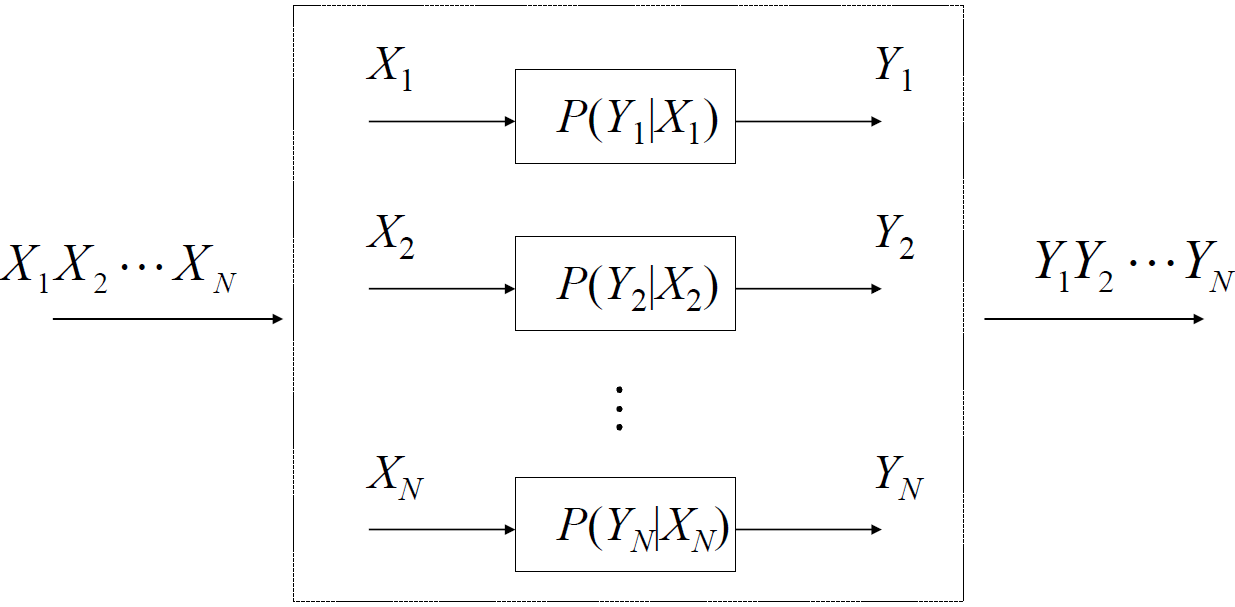
• I (X,Y;Z)表示从随机变量Z中获得的关于联合随机变量X,Y的信息量。
• I (Y;Z)表示从随机变量Z中获得的关于随机变量Y的信息量。

• I (X;Y)和I(X;Z)分别表示随机变量X和Y以及X和Z之间的信息量。

• 马尔可夫链结构级联信道

• 三个随机变量的马尔科夫链结构，对于XYZ三个随机变量，如果在XY条件下的Z只与Y有关（与X无关），即有

• 则称XYZ三个随机变量构成一个马尔柯夫链，记为

• 性质
  • 如果XYZ形成马尔柯夫链，则ZYX也是一个马尔柯夫链

• 如果XYZ形成马尔柯夫链，则有

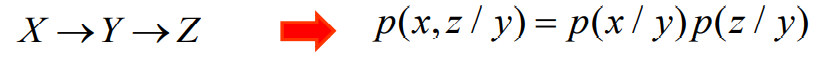
• 这个关系式称为X和Z条件独立于Y

• 级联信道的转移概率
  • 非马尔可夫链情况

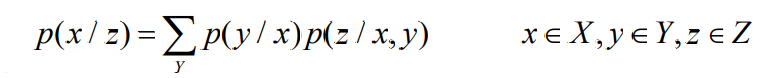
  - 矩阵表示

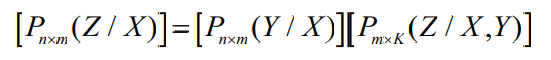
• 马尔可夫链情况

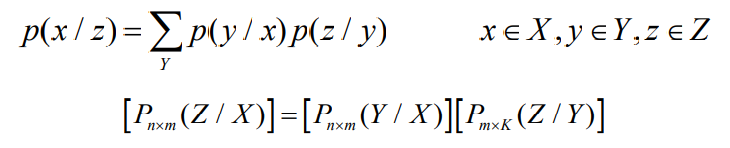
• 级联信道的互信息量
  • 定理：对于两个离散无记忆信道组成的串联信道，如果XYZ为相应的离散随机变量，则有

• 只有当时，才有等号成立
• 这个定理说明，对于串联信道，从Z中获得关于Y的互信息量一定小于等于从Z中获得关于联合随机变量XY的互信息量。
• 只有当时，即XYZ构成一个马尔柯夫链时，不等式的等号成立。

• 证明（Jessen不等式）：

• 定理：对于两个离散无记忆信道组成的串联信道，如果XYZ为相应的离散随机变量，则有

• 只有当时，才有等号成立
• 这个定理说明，对于串联信道，从Z中获得关于X的平均交互信息量一定小于等于从Z中获得关于联合随机变量XY的平均交互信息量
• 只有当时，即XYZ构成一个马尔柯夫链时，不等式的等号成立

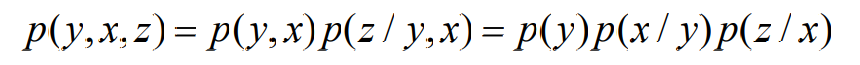
• 证明过程同上

• 定理：对于两个离散无记忆信道组成的串联信道，如果XYZ为相应的离散随机变量，并且随机序列XYZ构成一个马尔柯夫链时，有

• 只有当时，才有等号成立
• 如果XYZ构成一个马尔柯夫链，说明Z只取决于Y，所以I (Y;Z)大于I (X,Z)

• 如果同时YXZ也构成一个马尔柯夫链，则等号成立。这时说明X与Y完全相关，信道1为无噪声信道

• 定理：对于两个离散无记忆信道组成的串联信道，如果XYZ为相应的离散随机变量，并且随机序列XYZ构成一个马尔柯夫链时，有

• 这个定理也称为数据处理定理
• 如果我们把两个串联信道理解为数据处理系统，例如是取样、量化、编码、译码等，经过数据处理的交互信息量I (X;Z)小于等于I (X;Y)
• 数据处理定理说明，无论经过何种数据处理，不会增加信息量，只会减少

• 例题

4. 连续信道

4.1 连续随机变量的互信息

• 对称性
• 非负性

• 微分熵的概念

  4.2 连续有噪声信道

• 对于AWGN

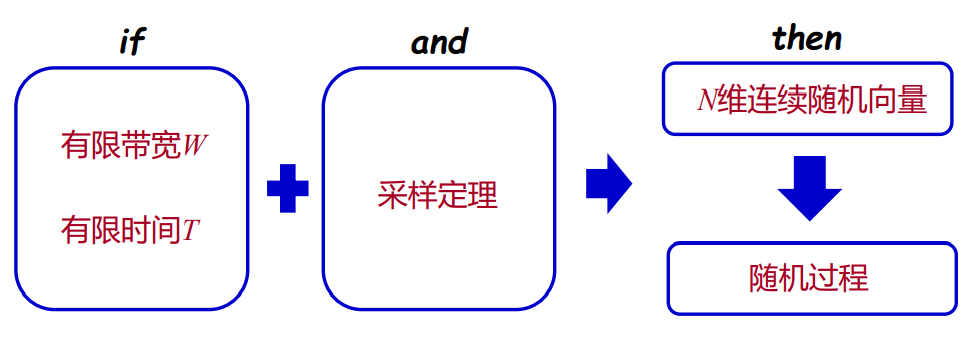
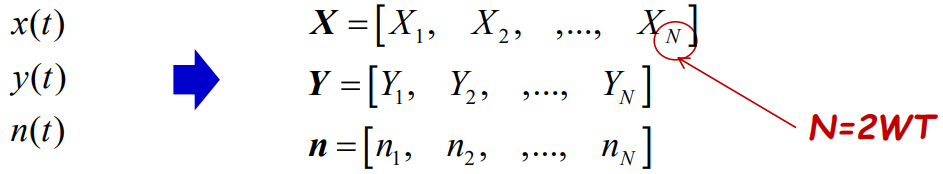
• 一维连续随机变量

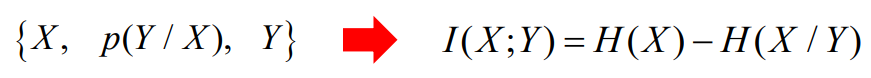
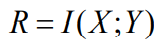
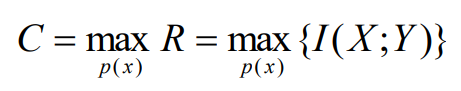
• N维连续随机向量

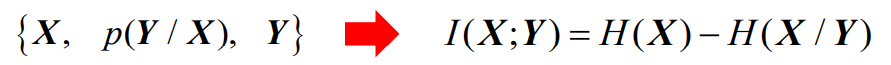
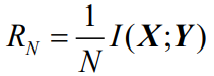
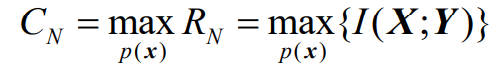
• 随机过程

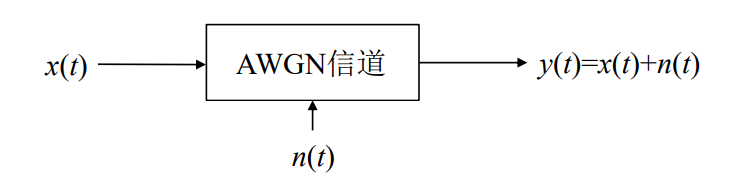
（带限随机过程）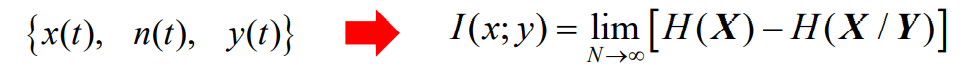

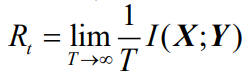
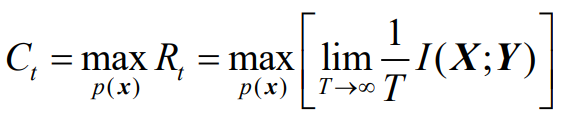
4.3 连续信道噪声熵

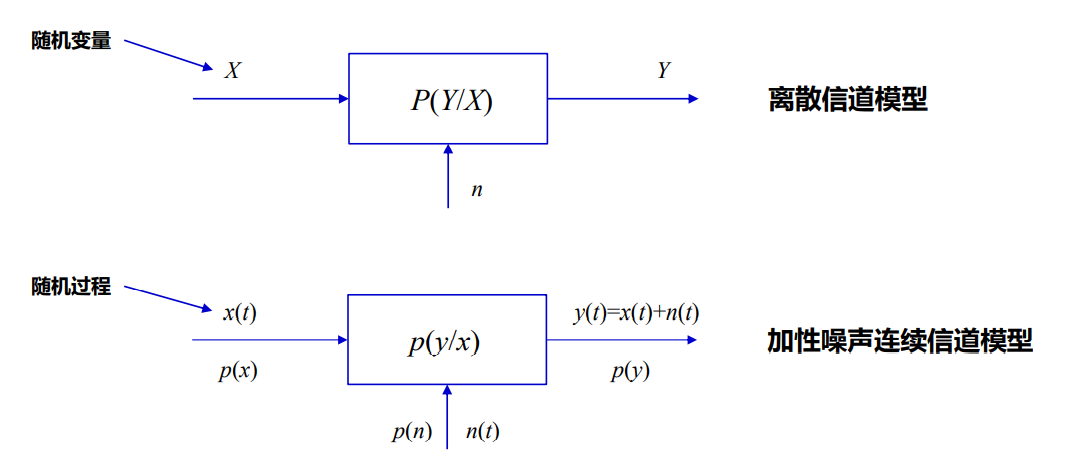
• 如果这种变换为确定的某种函数关系，则可以表示为

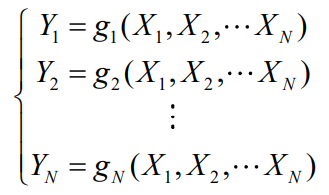
• 如果N维随机向量Y的每个分量Yi(i=1,2,…N)都是随机变量Xi(i=1,2,…N)的单值连续函数（偏导数存在）
• 则随机向量X也可以表示为随机向量Y的连续函数形式

• 根据概率论的结论，如果一个N维随机变量X映射成另一个N维随机变量Y，则样本x落入区域A的概率就等于样本y落入区域B的概率
• 即有：

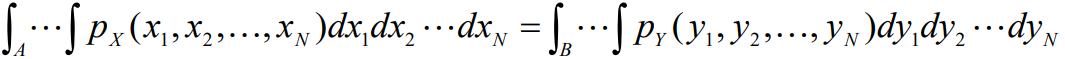
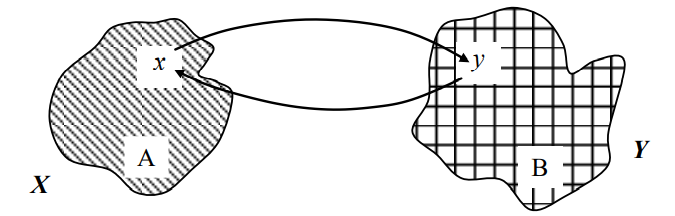
• 并且存在变换关系

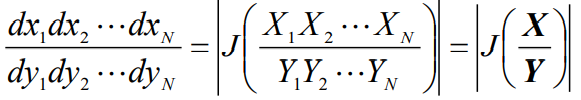
• 为雅可比行列式
• 因此有

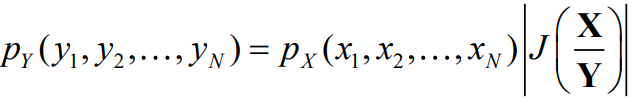
• 由此可见，除非雅克比行列式等于1，一般情况下，随机变量经过变换后其概率密度函数将发生变化
• 根据

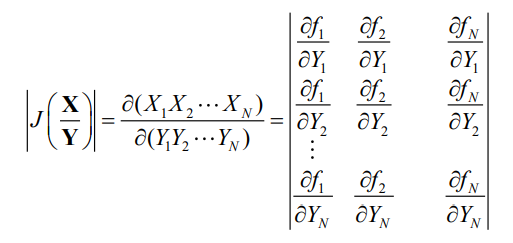
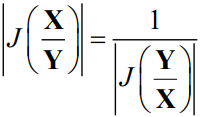
• 根据连续信源熵的定义，信源变换后的熵为

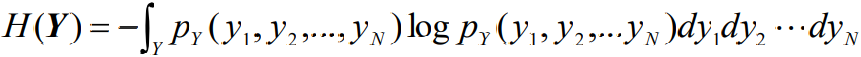
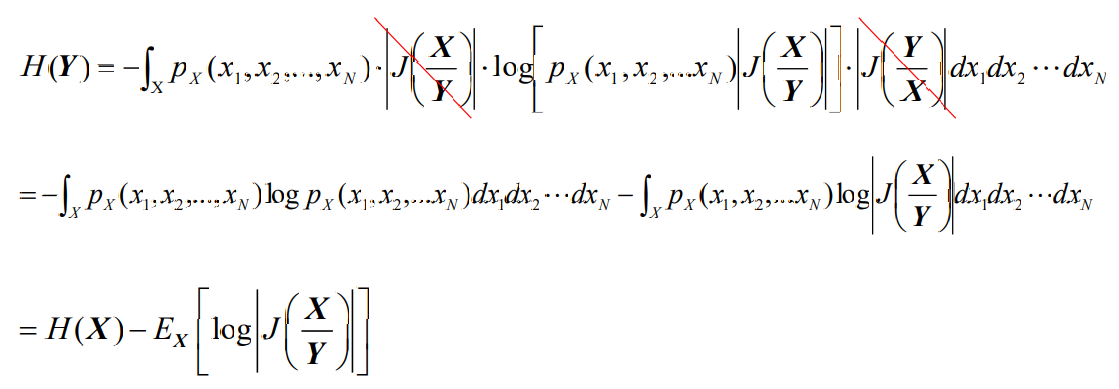
• 可见，连续信源经过信号处理之后上会发生变化，
• 这一点也是连续信源熵与离散信源熵可能存在的一个不同之处。
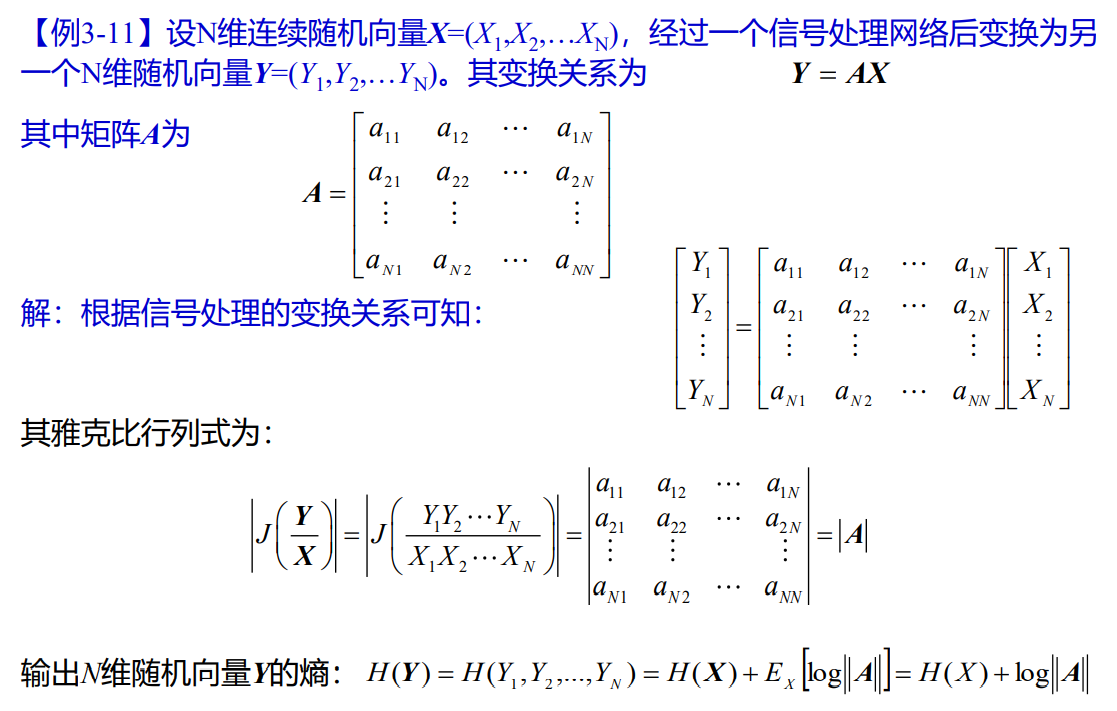
• 例题

• 经典信息论回答的两个基本问题

  • 无损信源编码（数据压缩）的极限值是信息熵H(X)
  • 无差错传输的最高速率是信道容量C=Rmax

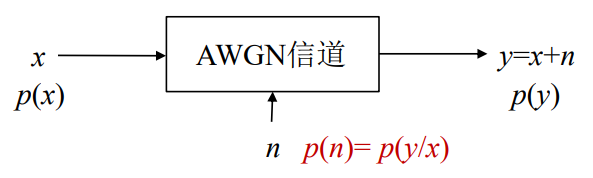
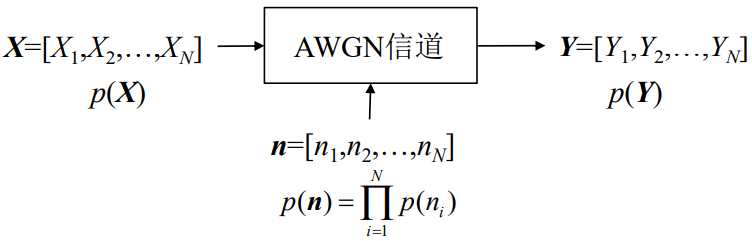
• 对于连续有噪声信道（AWGN连续无记忆信道）

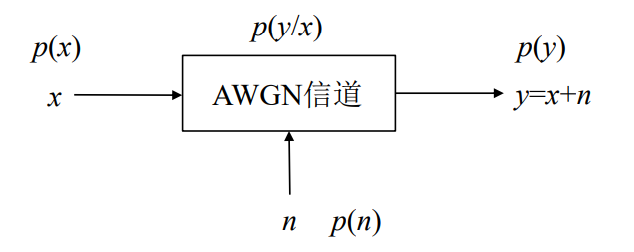
• 可以类比Z=X+Y模型

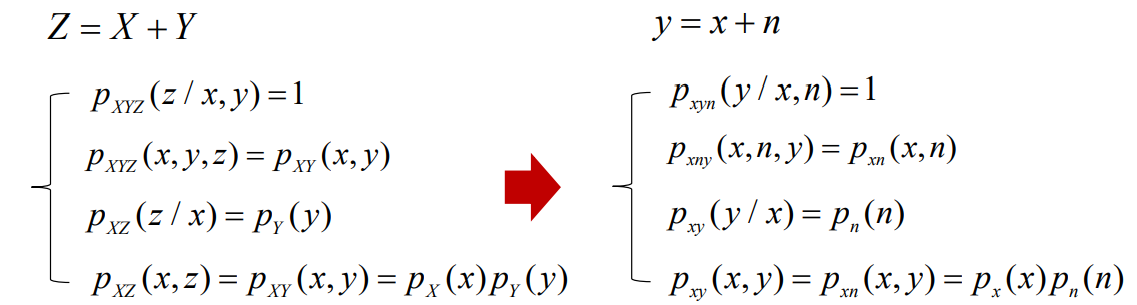
• 对于一个AWGN信道，信道的转移概率就等于噪声的概率密度函数；
• 也就是说，这时的条件熵H(y/x)就等于噪声熵H(n)。

4.4 一维随机变量AWGN信道

• 单符号
• 信道输入X和输出Y均为取值连续的一维随机变量，噪声n为加性高斯白噪声。
• 如果 n为一个均值为零，方差为σ 2的一维高斯白噪声，则其功率谱密度和熵分别为

• 进而得到一维连续信号在AWGN信道上的信道容量为：

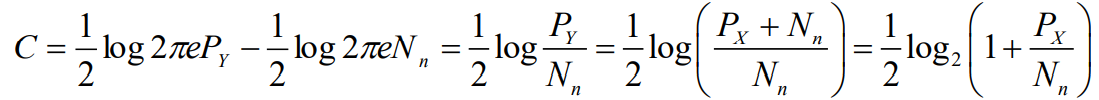
• 因此对于一维加性高斯噪声信道

4.5 N维连续随机变量AWGN信道

• 信道输入为N维连续随机信号X=(X1 ,X2 ,…XN )，信道输出为Y=(Y1 ,Y2 ,…YN )。噪声为 n=(n1 ,n2 ,…nN )为零均值高斯白噪声，如果信道是无记忆的，有

• 由离散无记忆信道平均互信息量小于单符号平均互信息量之和的定理得到

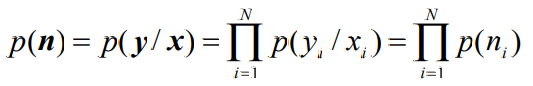
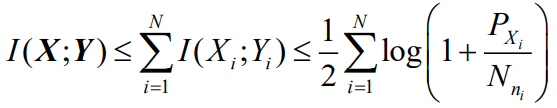
• 信道容量为

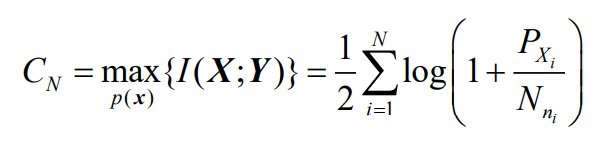
• 如果N维无记忆信源的每个分量方差相等，N维高斯白噪声的每个分量方差也相等，则N维无记忆加性高斯白噪声信道的信道容量在数值上就等于单符号AWGN信道的信道容量的N倍。即

4.6 随机过程AWGN信道

• 在通信理论分析中最常用的就是加性高斯白噪声信道，信道的输入输出为随机过 程x(t)和y(t)，噪声n(t)为零均值，功率谱密度为N0 /2的加性高斯白噪声。
• 假定信道 是有限带宽的，即f≤W，这样信道的输入输出及噪声都是带限随机过程

• 对于一个带限随机过程，我们可以通过取样将其转换为随机序列（随机向量）

• 在T时间间隔内，由于我们假设，N维高斯白噪声向量n=(n1 ,n2 ,…,nN ) 是独立同分布的

• 因此，其每个分量的功率（方差）为：

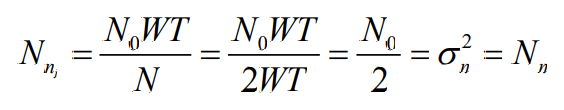
• 噪声的分量个数（维数）：

• 所以，噪声的每个分量的功率：

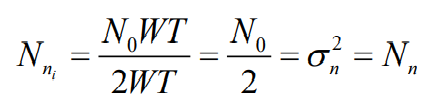
• 假设信道输入随机过程x(t)的受限平均功率为P，T时间内的总平均功率为TP，则N 维随机向量 X=(X1 ,X2 ,…XN )的每个分量的功率为

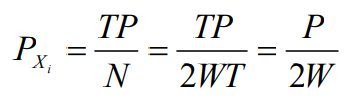
• 根据前面分析，有

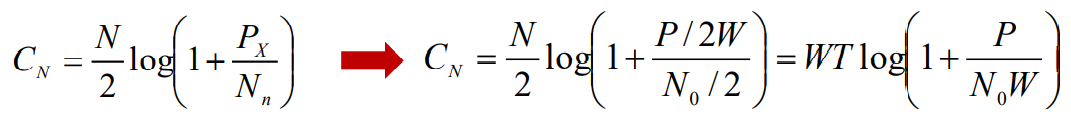
• 要达到这个信道容量（T时间内，N个符号的最大熵速率），要求输入的N维随机向 量X中的各分量都是均值为0，方差为P，相互独立的高斯分布随机变量。也就是说 ，信道输入的随机过程x(t)应该是平均功率为P的零均值高斯信号。

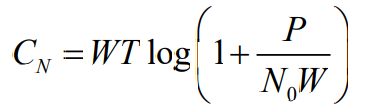
• 最后，随机过程AWGN信道上的信道容量为：

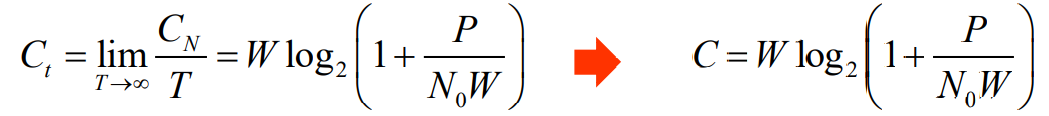
• 其中W为信道带宽，P为信号x(t)的平均功率，N0为单边噪声功率谱密度，N0W为带 内噪声平均功率。有时我们用B表示信道带宽，还有的时候我们用N表示噪声功率 ，并用C表示最一般情况下的信道容量，上式就写为

• 即为香农公式
• 香农公式表明，在加性高斯白噪声信道上，只有当输入信号是平均功率受限的高斯分布信 号时，熵速率可以达到此最大值。在理论上给出了高斯白噪声信道上最大信息传输速率的极限值。

5. 波形信道

5.1 连续信道的采样

• 连续信道频带带限于（0，B），则输入、输出和噪声都是限频的随机过程
• 抽样定理，将连续信道转换为离散信道
• 采样频率，即每秒传输2B个采样值

5.2 香农公式

• 当噪声是双边功率谱密度为的高斯白噪声时

• 也可以写作

• 在一个点对点AWGN无记忆信道上，输入信号x(t)为带限连续信号，信号带宽为W，信号平均功率为P，信道的噪声功率谱密度为N0时，信道可以传送的最大信息速率C
• 证明思路

• 证明过程见前文随机过程AWGN信道容量分析
• 对于噪声功率谱密度一定的无记忆高斯白噪声连续信道，其信道容量C与信号带宽W和 信号噪声功率比P/N有关
• 对于平均功率受限的连续信源，当信源信号X为高斯分布时，熵速率等于信道容量
• 对于连续信道，高斯白噪声信道危害最大，因为噪声熵H(n)最大使熵速率R减小
• 公式给出了信道容量的极限值，在实际通信系统中往往是难以实现的，因为实际信源 不可能为高斯分布
• 高斯白噪声信道只是一个典型的连续信道模型，实际信道可能是非高斯信道，非高斯 白噪声信道的信道容量计算比较复杂，在工程上一般都用高斯白噪声信道来估算信道 传输性能

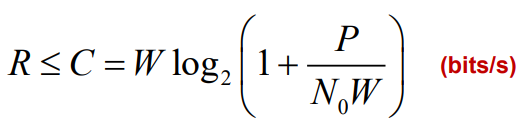
• 在实际通信系统中，任何点对点AWGN信道上，实际的信息传输速率（熵速率R） 将不会超越信道容量
• 如果是信道带宽W增加，也不会提高信道容量

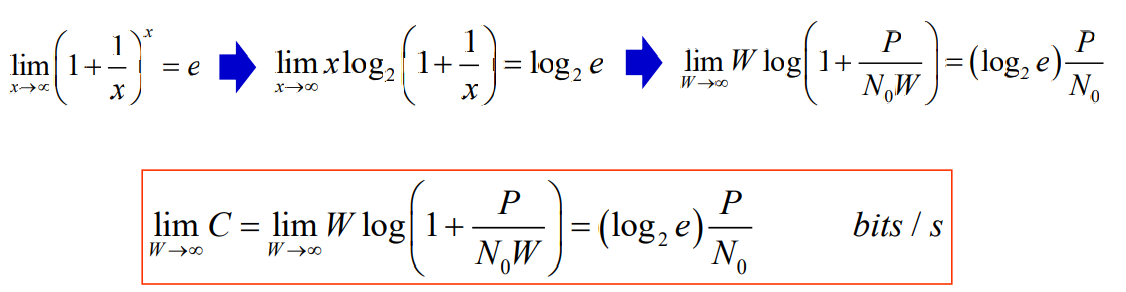
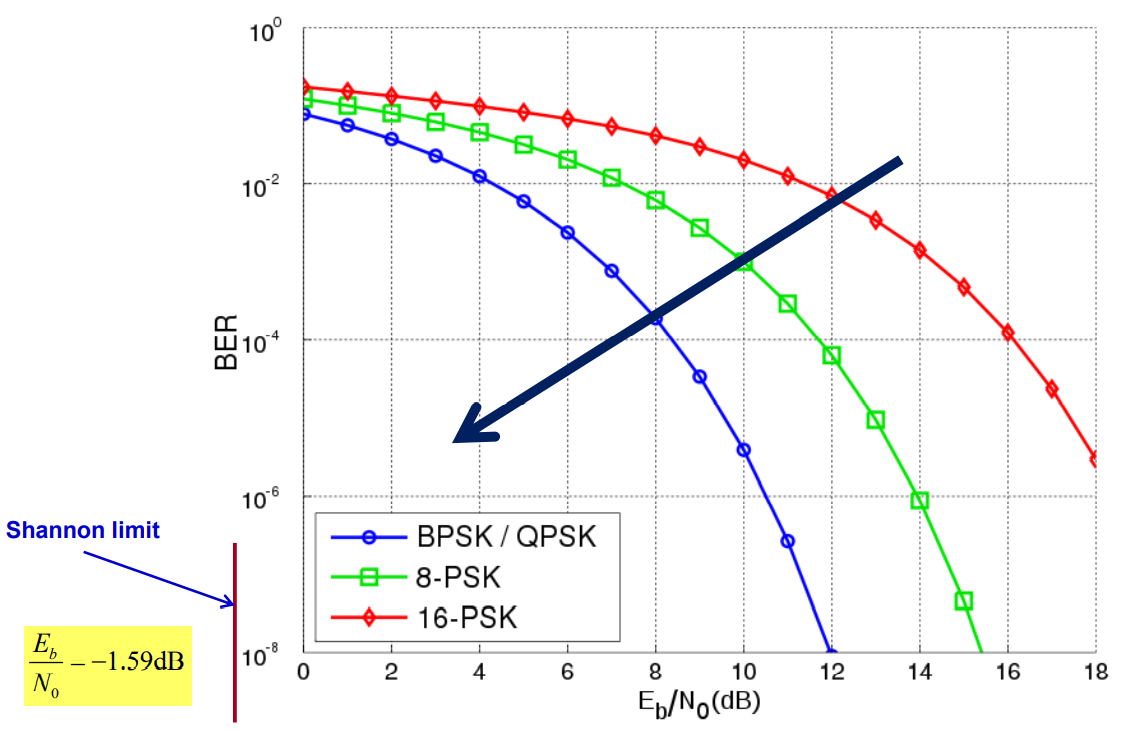
• 表明：当带宽趋于无穷大时，无差错传送1bit信息所需要的最小信噪比为

• 这是一个非常小的信噪比，称为香农限

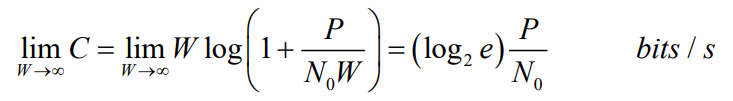
• 传送1bit信息所需要的信噪比：