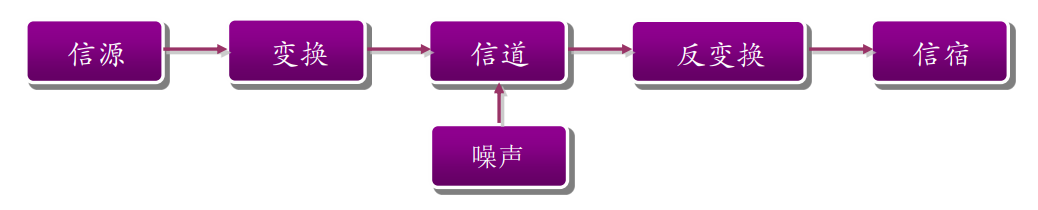
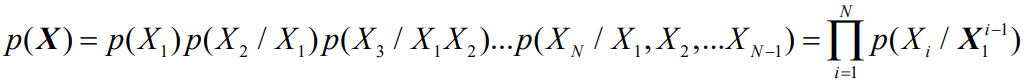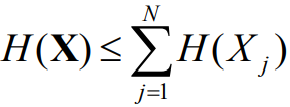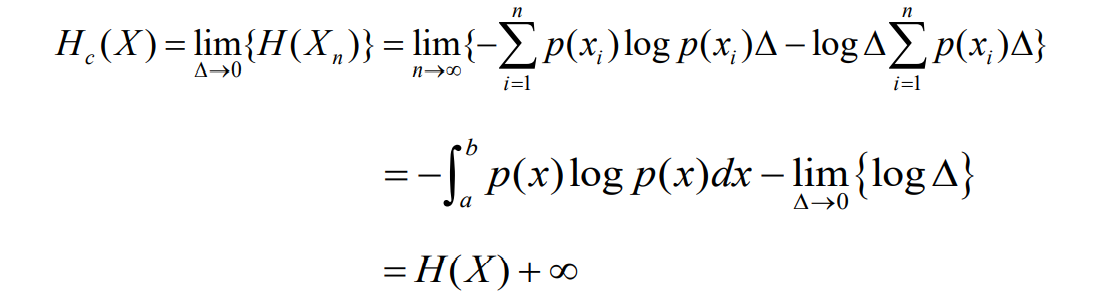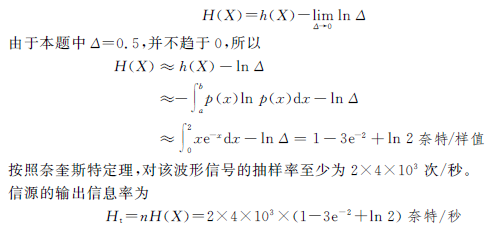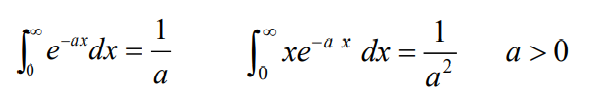通信系统
评价指标
- 有效性就是用尽可能短的时间、频带、功率和成本传送一定数量的信息。
- 例如,用信息传输速率描述时间有效性,用频带利用率描述频率有效性等,对于数字通信系统来说,信源编码是提高系统有效性的主要手段
- 可靠性就是要使信源发出的消息经过信道传输后,尽可能准确、不失真地再现在接收端。
-
广义信息
语法信息
- (grammatical information)只在形式上表征事物状态和运动规律,只研究状态个数和状态之间的关系,不研究状态的含义。是信息的最基本形式,也是最简单的形式。香农定义的信息就是一种语法信息,即从概率统计的角度来研究事物运动状态及状态变化的关系。
- 语义信息
- (semantic information)可以表示出事物状态和运动规律的具体含义和影响,即研究信息的具体含义。语义信息比语法信息更为复杂,更为具体。就是语言中包含的信息,它不仅包括语言自身的信息,还包括知识提供的信息。语义信息是信息的复杂形式。具有一定主观性,具有不统一的度量标准,仍在发展中。
语用信息
信号
- 信息的物理表达层,是三个层次中最具体的层次。它是一个物理量,是载荷信息的实体,可测量、可描述、可显示,如电信号、光信号、声信号等
- 消息
- 或称为符号,是信息的数学表达层,它虽不是一个物理量,但是可以定量地加以描述,它是具体物理信号的进一步数学抽象,例如文字、数据、代码、图形等。
信息
- 信息是指各个事物运动的状态及状态变化的方式。人们从来自对周围世界的观察得到的数据中获得信息,信息是信号与消息的更高表达层次。
香农信息论认为信息的多少等于无知度的大小,不确定性的大小,因此,香农信息也称为概率信息。信息是可以传递的,具有不确定性的消息(情报,数据,信号)中所包含的表示事物特性的部分。
概率论公式
基础公式
当X与Y相互独立时
全概率公式
贝叶斯公式
解释:
信息量
自信息量
- 单符号离散信源的数学模型
- 信源符号不确定性的度量,个值
- 一个符号不确定度(随机变量单个样本)就是它的自信息量
- 对于信源空间
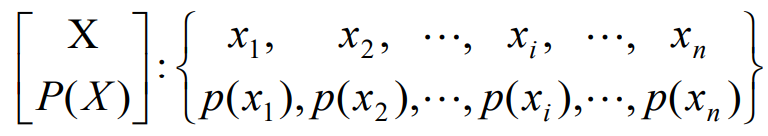
- 完备空间
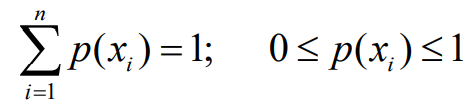
- 则任意一个信息符号x_i的不确定度为
- 称为哈特莱公式
- 自信息量即为K=1的哈特莱公式
互信息量
信息熵
平均自信息(信源熵)
- 随机变量的平均不确定度
- 熵函数是随机变量自信息量(不确定度)的数学期望
- 离散无记忆信源的熵
- 信源X在没有发出符号以前,接收者对信源的平均不确定度
- 非负性,对称性,确定性,最大值
- 离散信源最大熵
联合熵
- 联合信源的信源空间
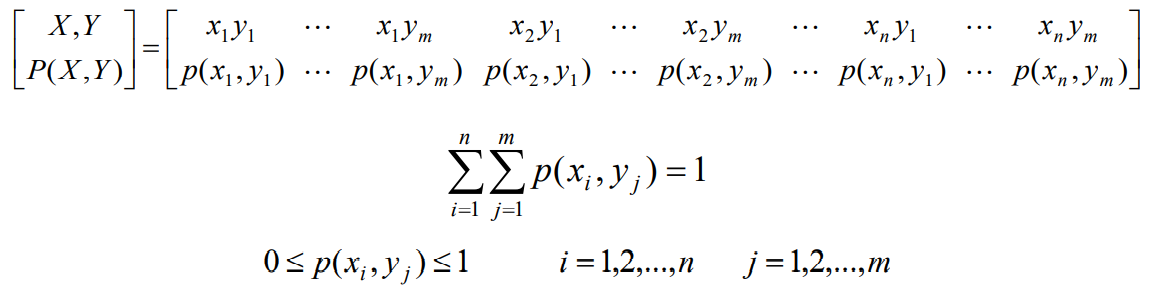
- 二元联合信源的输出一个消息符号(xi,yj)所发出的平均信息量称为联合熵,其熵函数的表达式为
- 对于三元联合熵,联合熵的链式规则来自于联合概率的链式规则
条件熵
- 二元联合信源输出Y(或X)任一状态后, 再输出X(或Y)任一状态所发出的平均信息量称为条件熵
- 其熵函数的表达式
平均互信息
注意:互信息可正可负,但平均互信息一定为正
熵之间的关系
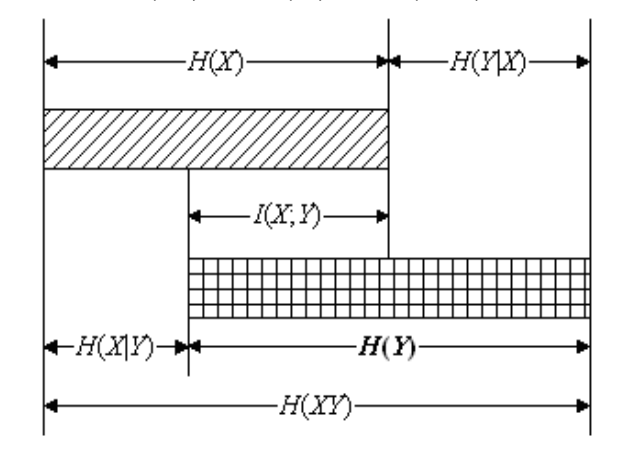
- 当XY相互独立,其联合熵等于两个随机变量独立熵之和,而条件熵等于独立熵
-
相对熵
是两个随机分布之间的“熵距离”的度量
- 相对熵D(p//q)可以用来表示:当真实分布为p,而估计分布为q时的估计无效性(差异)
- 相对熵函数表示为
- 相对熵为两个随机分布的对数似然比的数学期望
- 也称为Kullback-Leibler距离(KL散度)
- 相对熵大于等于零,当且仅当p=q时为零
- 实际意义
- 如果一个随机变量有两种不同分布
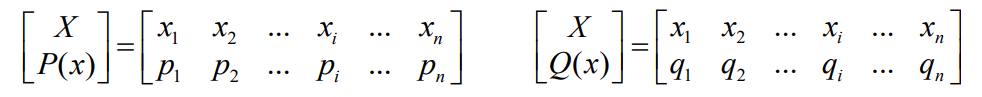
- 则一定存在
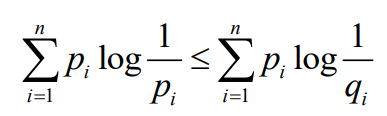
- iff pi=qi时等号成立。这个关系称为Gibbs不等式
- 由此可知
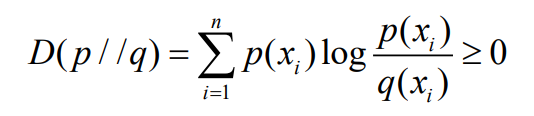
-
信息增益
决策树(Decision Tree)中利用了信息熵的概念,定义了一种所谓的信息增益
- 简单定义:
- 特征A(参数)对训练数据集D(变量)的信息增益:定义为集合D的信息熵H(D)与参数A给定条件下D的条件熵H(D/A)之差,即
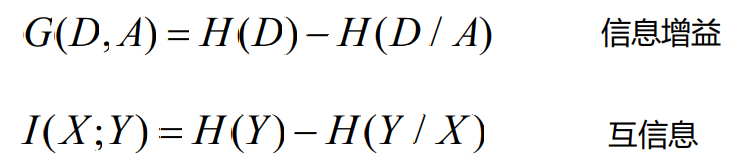
- 信息增益的形式与互信息量I(X;Y)一样,等于一个随机变量的熵与其条件熵之差
- 信息增益就是一个变量X对于另一个随机变量Y的影响,
- 信息增益越大,说明X对Y的影响越大(关联性越强)
- 信息增益越小,表示X对Y的影响越小
决策树为机器学习中的一种分类算法,在计算机的数据挖掘领域被提出,也称为分类树、判断树
信息是负熵
在香农提出信息熵概念之后,很多学者描述信息是负熵。
- 其基本含义是:系统状态(符号)的无序性使熵增加,越无序熵就越大
- 而获得信息的过程是使熵减小的过程,我们定义的互信息量等于先验熵减去后验熵,也是使熵减小的过程
- 信息量等于系统熵的减少量
- 例题
数据处理定理
平均条件互信息
平均联合互信息
数据处理定理
X,Y,Z构成一个马尔可夫链
表明从Z得到信源A的信息量永远小于等于从Y得到信源A的信息量
解释:X → Y →Z
如果视Y到Z为对数据的处理过程,无论怎么处理都会损失损失一部分信息量,最多保持原有信息量,间接经验永远没有直接经验实在
即为 信息熵不增原理
信源
基本概念
信源熵表示
扩展信源
可以将多符号信源
中的n个符号视为1个符号,即将信源N次扩展
则随机变量数为(q为每个符号的变量数,N个符号的排列组合)
N次扩展信源表示为
- 如果一个N维扩展信源是由一个单符号离散信源扩展而成
- 其中的单符号信源的空间为
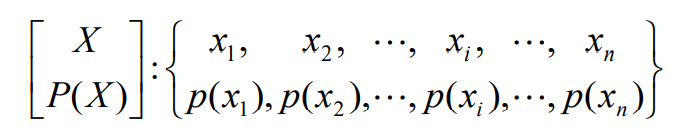
- 这时,N维扩展信源的空间为
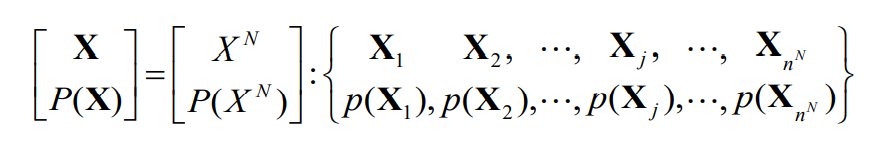
- 同时有
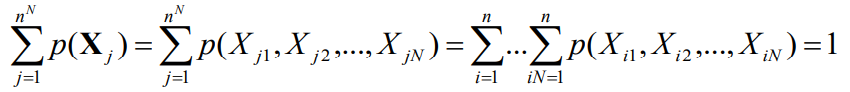
- N维扩展信源熵
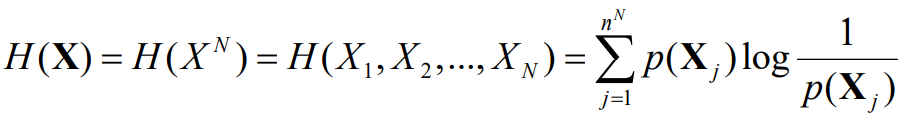
- 如果N维扩展信源的符号间相互独立
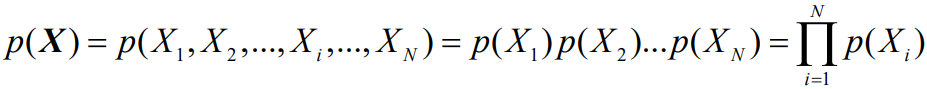
- 如果不独立
注意区分
离散平稳无记忆信源(DMS)
离散平稳有记忆信源
信源熵
可以根据联合熵和条件熵的关系理解(熵的链式法则)
注:其中随着X的增加而逐渐减小
随着处理环节的增多,熵的不确定性越来越小
理解可以参考 [数据处理定理](#x8oX1) (信息熵不增定理)
熵率
极限必然存在
称为离散平稳有记忆信源的极限熵
存在大小关系:
等号仅在无记忆信源时成
- 例题






- 扩展信源的熵实际上就是一个联合熵。根据熵函数的性质,条件熵小于等于独立熵,可以得到结论:有记忆扩展信源的熵小于等于两个独立信源熵之和
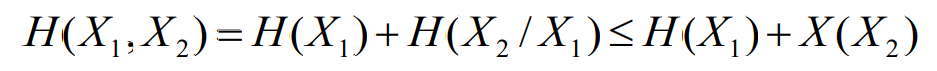
- 对于N维扩展信源,有记忆N维扩展信源熵小于等于无记忆N维扩展信源的熵
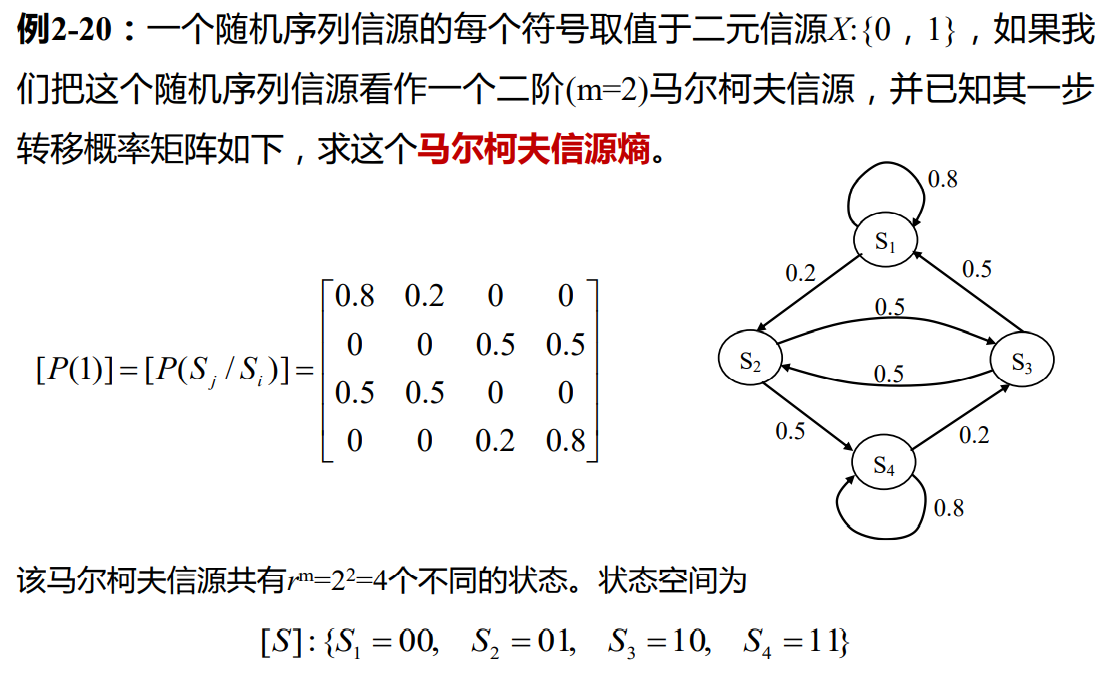
马尔可夫信源
状态转移概率
将符号或符号的组合视为一个状态,下一个符号出现的概率只与当前的状态有关而与该状态之前的历史符号无关
将符号的条件概率问题变成状态转移概率
一阶马尔可夫信源的状态转移概率即为信源输出符号的条件概率
状态的转移可以从状态机的状态切换上理解,当以某种概率产生了一个新符号时,即以该概率实现了一次状态转移
如N阶马尔可夫链
由状态转移概率组成转移概率矩阵
时刻,
的状态为
的条件下,经过
步转移到达状态
的概率
为步转移矩阵
齐次马尔可夫链
当状态转移概率只与状态及时间间距有关,而与时间起点无关
即
时,称为时齐马尔可夫链或齐次马尔可夫链,也称为具有 平稳转移概率的马尔可夫链 。
注意,这里还 不能称为平稳过程
对于齐次马尔可夫链,一步转移完全决定了步转移概率
因此在求某时刻的状态概率分布
记表示初始概率
有
稳定马尔可夫链
绝对概率
当极限存在,且与初始初始状态无关,则将
称为平稳分布的
此时满足
此时马尔可夫链达到了稳定的分布,稳定分布只与转移概率有关,而与初始分布无关。
遍历性(各态历经性)
满足
此时分布称为极限分布或平稳分布
这时信源才是一个离散平稳信源
稳态分布的判断和求解
马尔可夫链稳态分布存在的充要条件是,存在一个正整数,使矩阵
中的所有元素均大于零
求解时满足
将作为未知数带入方程求解
平稳概率分布
符号的平稳概率分布与状态的平稳概率分布
区分
不考虑符号的相关性,则由符号的平稳概率分布可得信源熵
考虑符号的相关性,信源的熵率如下
马尔可夫信源熵
推导顺序
- 已知
符号条件概率- 即知道在各种状态下产生下一个符号的概率
- 可枚举推出
状态转移概率- 即知道由一个状态切换到另一个状态的概率
- 可通过
得知
稳态分布概率- 即达到稳定分布后各个状态的概率
- 再用
得知
稳态符号概率- 即达到稳定分布后各个符号的概率
- 如果不考虑符号相关性,由
即可得知符号熵
- 如果考虑符号的相关性,即求信源的熵率
- 即为信源的稳态分布概率乘上条件熵
- 例题
信源的相关度和相对度
- 香农信息论讨论信源熵只是真实信源的一种模型化和简化
- 实际信源往往是非平稳的有记忆随机序列信源,其极限熵的计算太复杂,解决的方法是假设其为离散平稳随机序列信源,极限熵求解也比较难
- 进一步假设其为m阶马尔柯夫信源,用其极限熵Hm+1近似
- 或者假设为N维扩展信源,其熵为
- 最简化的信源是离散无记忆信源,其熵为
- 最后,先验等概的离散无记忆信源,其熵所谓最大熵为
- 存在大小关系
- 符号间相关性越大,熵越小。离散有记忆信源的记忆长度越长,信源熵越小,而独立且等概的信源具有最大熵
熵的相对率
信源的剩余度
冗余度
表示信源在实在发出信息时所包含的多于信息
- 信源符号间的相关性
- 相关程度越大,信源的实际熵越小
- 信源符号分布的不均匀性
- 等概率分布时信源熵最大
掌握即掌握了信源的全部规律,但不现实,掌握有限
,与理论极限值相差,即可得知信源的冗余度
连续信源
- 信源的 消息符号在时间上和状态取值上都是连续的
- 时间离散状态连续的信源熵可以用连续信源熵表示,相当 于一个连续随机变量
- 而时间连续的信源,为一个随机过程,只要信号频谱有限 ,则可以根据采样定理,将其变为时间离散信源
- 如果一个信道的输入输出都是连续随机变量或随机过程, 则称这个信道为连续信道
从随机变量的角度看,连续熵就是连续随机变量的熵,也称 为微分熵(differential entropy)
连续信源的样本个数是无限个,样本概率用概率密度来表示。如果连续随 机变量X,如果样本取值为实数域R,其概率密度函数为p(x),则有
- 如果样本取值为一个有限实数域[a, b],则有
- 这时,连续随机变量X在某一状态x1的概率分布函数为:
- 这个连续信源的数学模型可以表示为
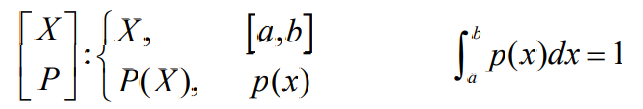
- 连续变量可以看作离散变量的极限情况,因此,可以利用离散信源熵的概 念来定义连续信源熵,首先,看一个在[a, b]区间取值的连续随机变量X
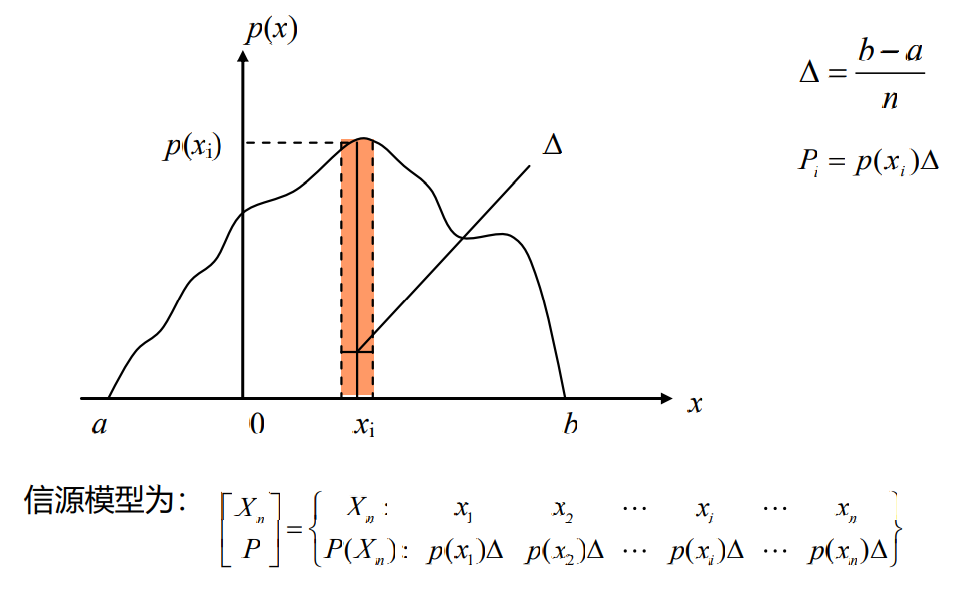
- 根据离散随机变量熵的定义,可得这个等效离散随机变量Xn的熵
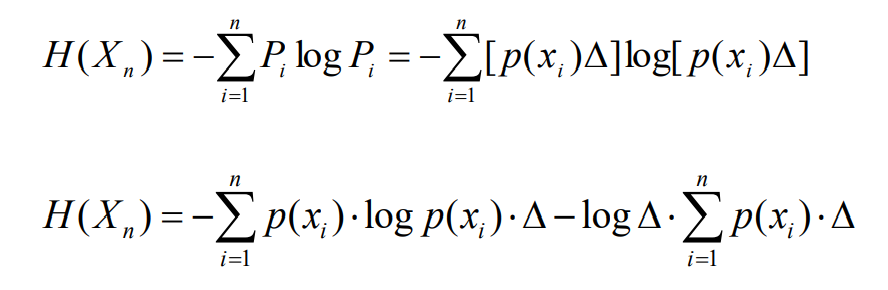
- 当n趋于无穷时,就得到连续随机变量的熵:
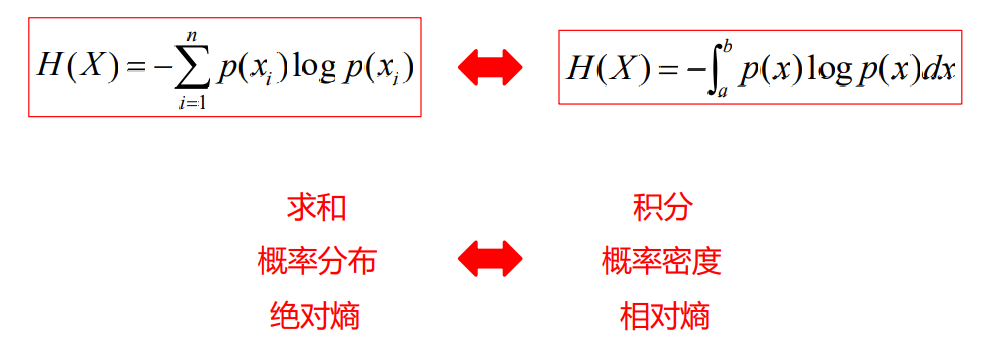
对比
- 离散信源熵
- 连续信源熵(绝对熵)
- 第一项为定值,第二项为无穷大量,连续信源的熵实际上是无穷大量,连续信源可能取值是无限多的,不确定性也是无限大的
- 严格地讲,连续随机信号熵不等于一个消息状态的平均信息量,其熵 是有限的,而信息量是无限的
- 连续信号熵不具有非负性,熵可以为负值
- 例题
微分熵
连续信源绝对熵的第一项即为微分熵,也称为差熵
具有非负性
- 联合熵
- 条件熵
与离散变量一样的相互关系
注:连续信源的熵为无穷大,但是微分熵是有限值
正态分布的连续信源的微分熵与数学期望无关,只与方差有关
几种连续信源的熵
- 均匀分布的连续信源熵(Uniform distribution)
- 设一维连续随机变量X 的取值区间是[a, b],X 在[a, b]中的概率密度函数是
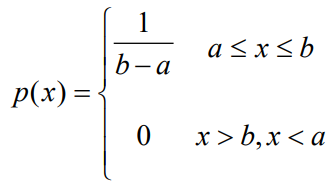
- 这种连续信源称为均匀分布的连续信源,其熵为
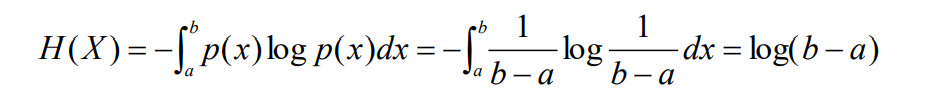
这时可以看到,当(b-a)<1时,H(X)<0,即连续信源熵H(X)不具有熵函数的非负性,因为H(X)是相对熵 ,相对熵可以为负值,但绝对熵仍然为正值。
高斯分布的连续信源熵(Normal distribution)
- 设一维随机变量X的取值范围是整个实数R,概率密度函数为
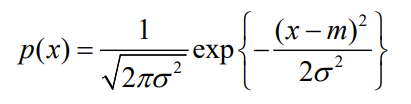
- 其均值和方差为
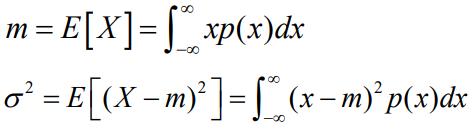
- 这时,可以得到0均值的高斯分布的连续信源(m=0)的熵为:
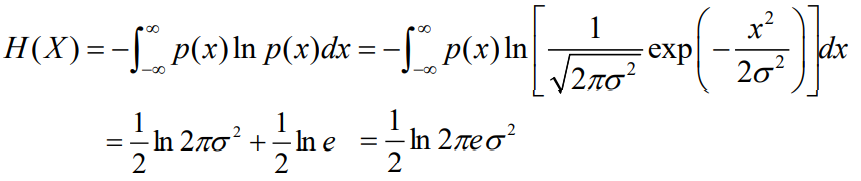
- 当均值为0时,高斯分布的信源熵为
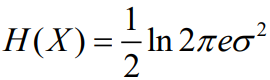
- 指数分布的连续信源熵
- 设一随机变量X 的取值取间为[0,∞],其概率密度函数为
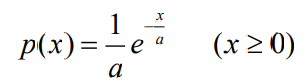
- 则称为指数分布的连续信源。其中常数a 为随机变量X 的均值。即
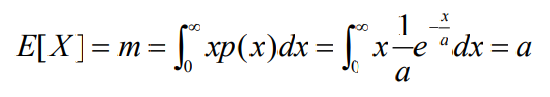
- 指数分布的连续信源的熵为
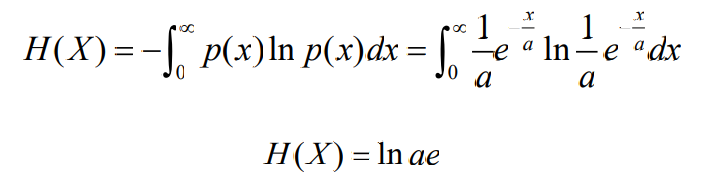
- 其中利用积分关系
连续信源的最大熵
- 利用数学方法(拉格朗日乘数法)可以求出连续信源的最大熵问题
- 即针 对一定约束条件,确定信源为如何分布能使连续信源获得最大熵
- 连续信源的熵为
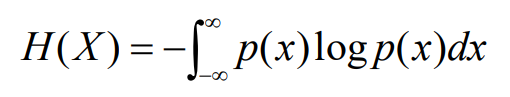
- 其基本约束条件为
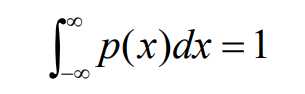
- 其它约束条件
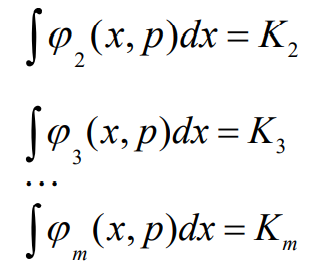
- 建立辅助函数
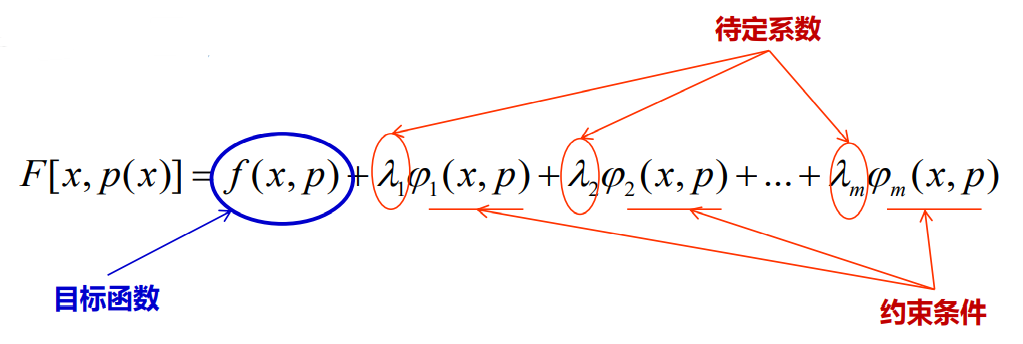
- 求这个辅助函数关于信源概率密度函数的微分,根据极值的条件有:
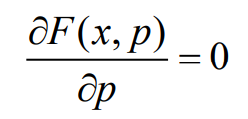
- 如果考虑m个约束方程,能够求得概率密度函数的解,
就可以确定这个连 续信源的最大熵和所对应的信源概率密度分布p(x)
得出结论
- 幅度受约束的连续随机信号均匀分布熵最大
- 概率分布为
- 幅度受约束的连续随机信号均匀分布熵最大
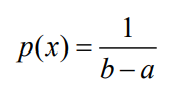
- 熵为
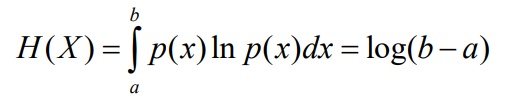
- 功率受约束的连续随机信号高斯分布熵最大
- 平均功率
- 概率分布为
- 平均功率
- 熵为
为什么高斯分布熵最大
讨论点对点连续有噪声信道,在这个点对 点的信道模型中,有三个连续随机变量x(t),n(t),y(t)
- 如果N维连续随机变量(连续随机向量)X=(X1 ,X2 ,…XN )的每一维都是高斯 分布的,则称为N维连续随机变量(N维高斯信源)
- 每个分量可以表示为:

- 根据概率论,各分量的协方差(联合二阶矩)为:
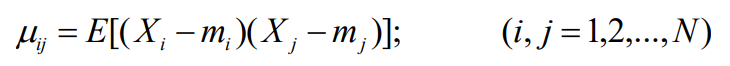
- 协方差矩阵
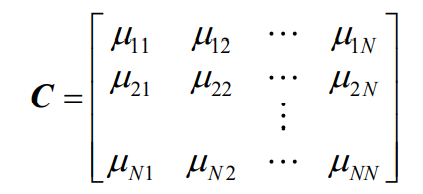
- 协方差矩阵的行列式为

- 当i=j时,也就是对角线上为随机变量Xi的方差
- 每个元素的代数余因式为:
- 则,N维连续随机变量的概率密度函数为:
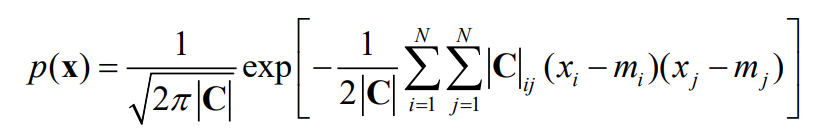
- N维连续随机变量的熵为:
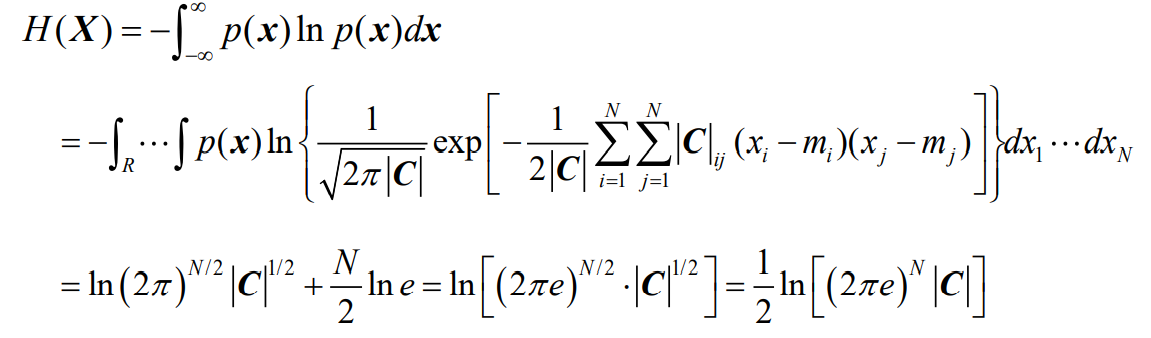
- 如果N维高斯分布的连续随机变量的是独立同分布的,即
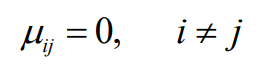
- 并且有
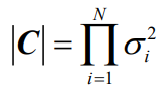
- 这时,称其为N维无记忆高斯信源,其熵为
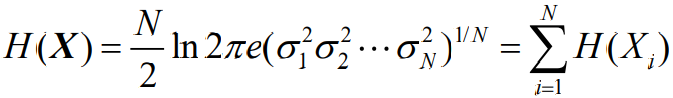
- 可以看到,对于N维高斯随机序列信源可以得到与N维离散序列信源相类似的结果,即无记 忆随机序列信源的熵等于各随机变量熵之和
连续信源的熵功率
- 研究均值为0,平均功率受限的连续信源
- 均值为零,平均功率限定为P的连续信源当服从高斯分布时达到最大熵
- 即有
- 若平均功率一样,高斯信源的信源熵最大
若信源熵一样,高斯信源的平均功率最小
定义熵功率为:一连续信源,将它视作高斯信源时的平均功率为它的熵功率
,而它的实际功率为
- 满足
- 即把该信源假设为高斯信源后的功率为该信源的熵功率,一定小于它的实际功率
- 熵功率则用来描述连续信源熵的剩余度,即一个连续信源可以改善的等度
两者的差值即为连续信源的剩余度( 从功率角度理解剩余度 )