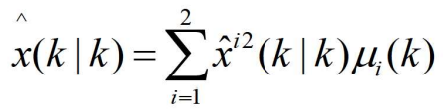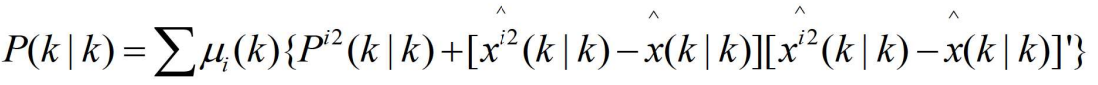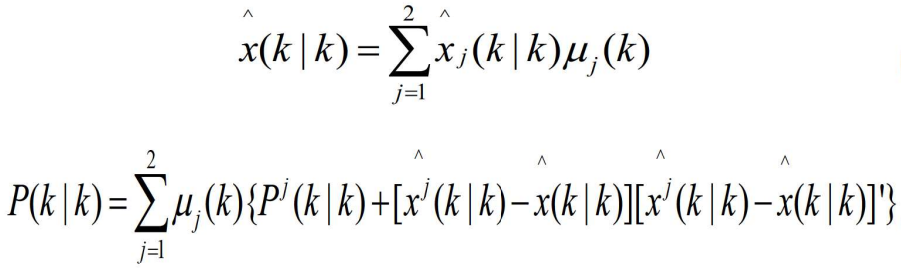6.1 多模型算法（Multiple-Model Approach）

  • 现实中不同目标或者同一目标不同时间的运动状态，所以只用一个过程方程来预测目标显然不合理，因此用多个方程描述，也称为多个运动模型
  • 在传统的机动目标跟踪方法中，虽然也用不同模型对应目标的不同运动状态，但通常每个时刻只一个模型滤波器在起作用，不同模型滤波器之间根据统计检验对目标状态进行监视和切换。尽管这样也能够适应目标机动运动的变化，但机动检测往往有滯后，而快速进行模型切换则可能降低滤波器的可靠性。
  • 多模型算法是一种递归算法。在这种算法中，每一个模型对应一个不同的过程噪声水平，多模型算法的基本思想如图所示。

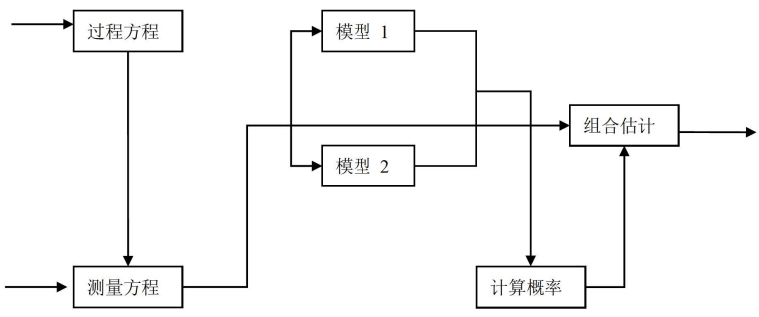
image.png

  • 多模型算法是一种基于“软切换”的机动目标跟踪方法。这种方法对于不同的目标运动状态或同一个目标的不同运动阶段，应用不同的模型滤波器组合。
  • 模型概率之间基于一个马尔可夫链进行切换。各模型滤波器估计的加权和作为最后的组合状态估计。
  • 设【数据融合】多传感器多模型概率数据关联算法 - 图2表示第j个模型是正确的这一事件，用

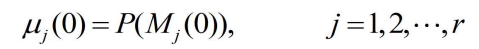
image.png

  • 表示模型【数据融合】多传感器多模型概率数据关联算法 - 图4的先验概率，用

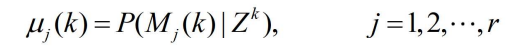
image.png

  • 表示模型【数据融合】多传感器多模型概率数据关联算法 - 图6在k时刻正确的概率，应用贝叶斯公式可得

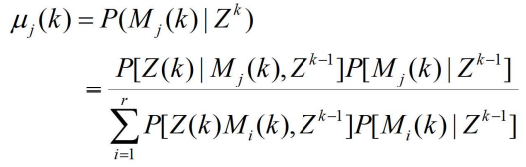
image.png

  • 应用下面两式

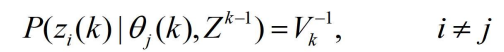
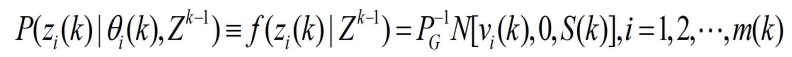
image.png
image.png

  • 可得

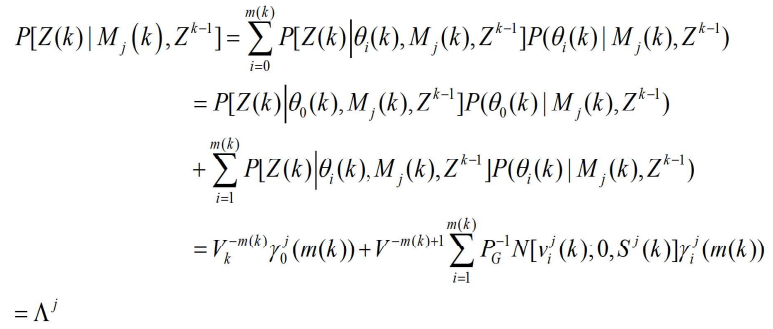
image.png

  • 其中

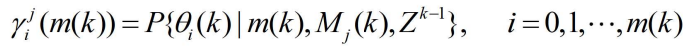
image.png

  • 【数据融合】多传感器多模型概率数据关联算法 - 图12表示对于模型 j 量测 i 的新息。
  • 由式

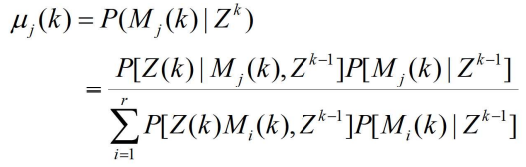
image.png

  • 容易得到

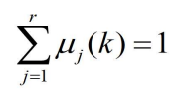
image.png

  • 多模型算法的状态更新估计，是以各种模型为条件的状态更新估计-一个加权和，即

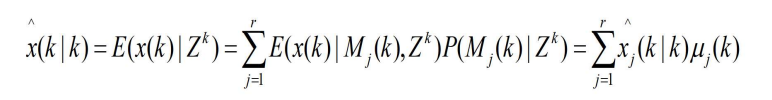
image.png

  • 其中

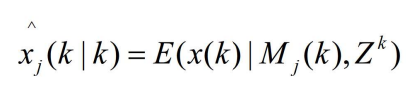
image.png

  • 表示以模型【数据融合】多传感器多模型概率数据关联算法 - 图17条件的状态更新估计。
  • 基于上面两式可以证明下式的协方差矩阵为

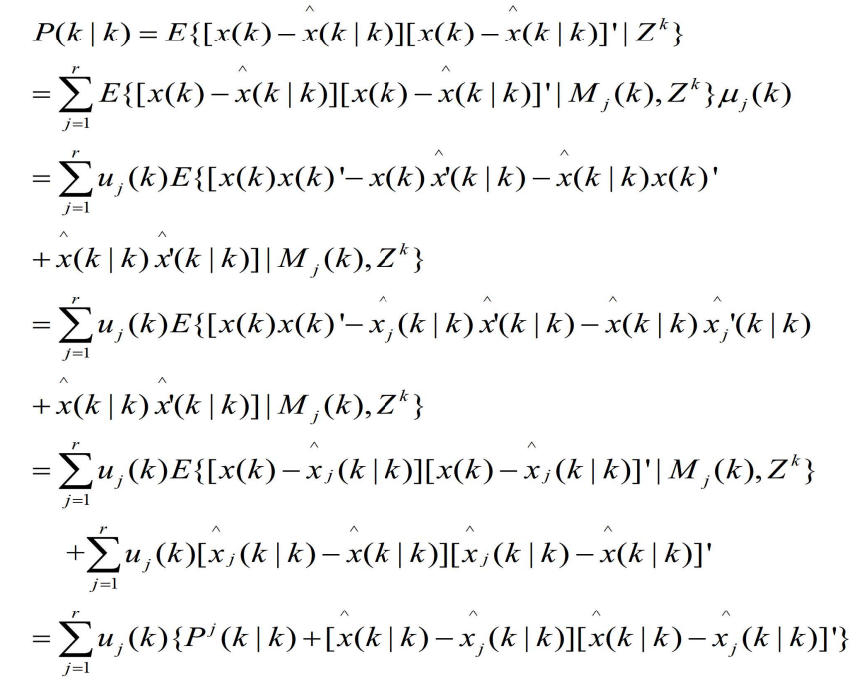
image.png

  • 其中

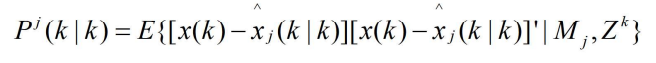
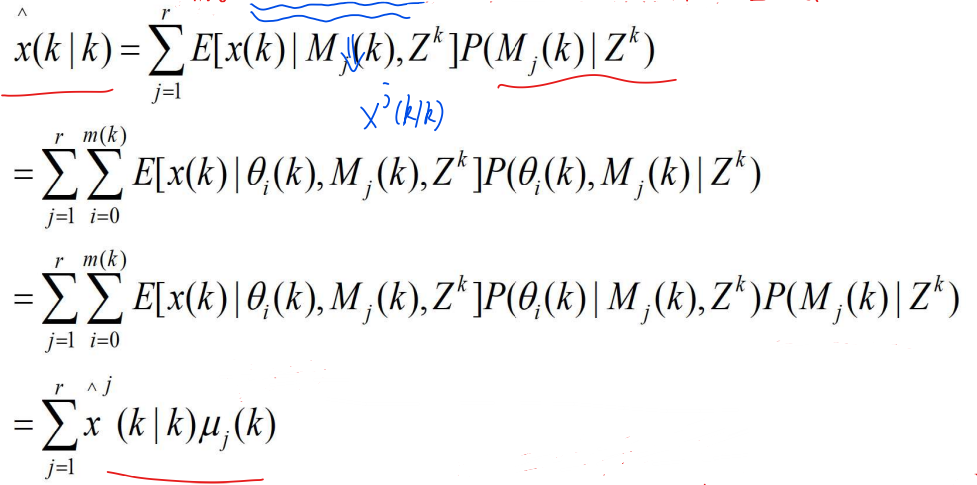
image.png

  • 表示以模型【数据融合】多传感器多模型概率数据关联算法 - 图20为条件的状态更新估计的协方差。

    6.2 相互作用多模型一概率数据关联算法

  • 相互作用多模型概率数据关联算法状态估计

image.png

  • 其中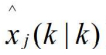image.png为模型j的概率数据关联滤波器输出
  • 相互作用多模型一概率数据关联算法的思想如图

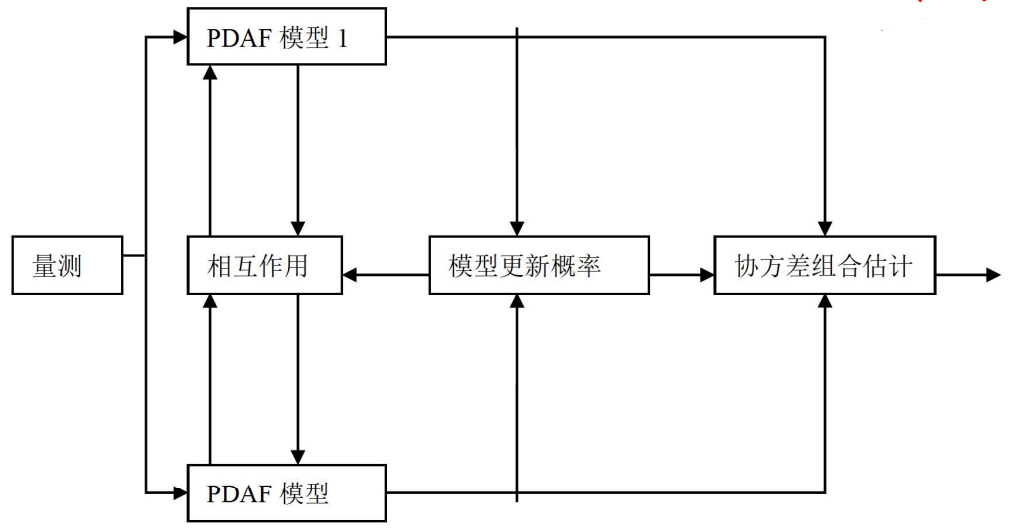
image.png

  • 由图看出，相互作用多模型一概率数据关联算法是一种递归算法。
  • 它假设模型的数量是有限的。算法的每一个循环包括4步：相互作用(混合)、滤波、模型概率更新计算和状态与其协方差的组合估计。在每一个时刻，假设某个模型在现在时刻有效的条件下，通过混合前一时刻所有滤波器的状态估计来获得与这个特定模型匹配的滤波器的初始条件。接着每个模型并行实现正规滤波步骤。然后，以模型匹配似然函数为基础更新模型概率，并组合所有滤波器修正后的状态估计(加权和)以得到状态估计。一个模型有效的概率在状态和协方差组合中起重要的加权作用。

  • 以下是针对两个模型建立的一个完整算法

  • （1）相互作用：

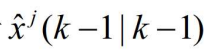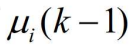    • 基于image.png和image.png，计算与模型j匹配的滤波器的混合初始条件。
    • 由全概公式和贝叶斯法则得

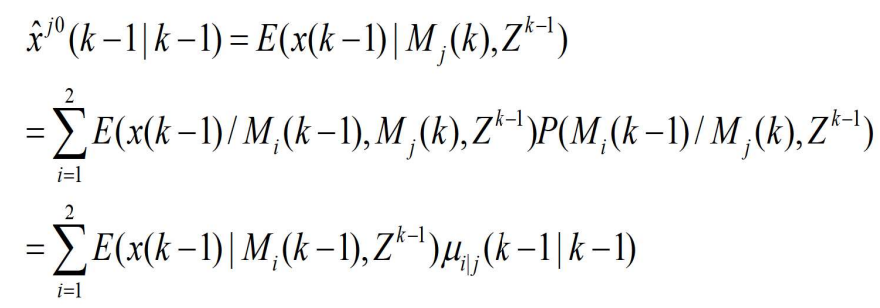
image.png

  • 其中

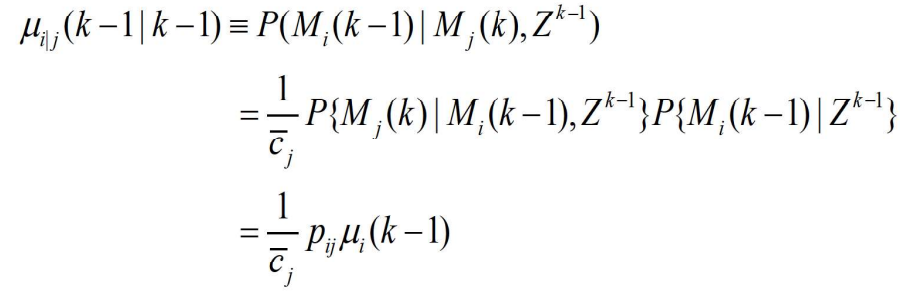
image.png

  • 其中

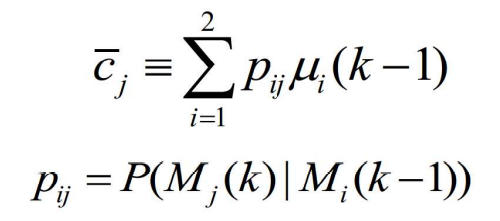
image.png

  • 是模型开关概率，通常认为其服从马尔可夫链，表示k-1时刻模型 i 到 k 时刻模型 j 的跳转概率。
  • 前式联立得

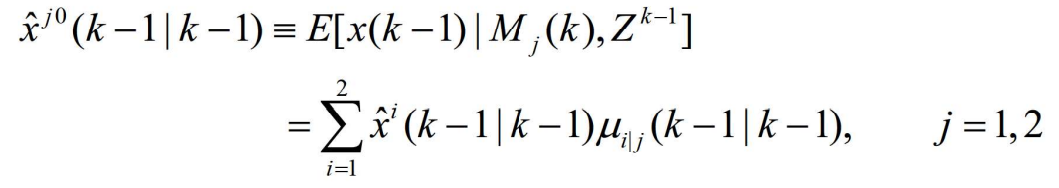
image.png

  • 也容易证明其相应的协方差为

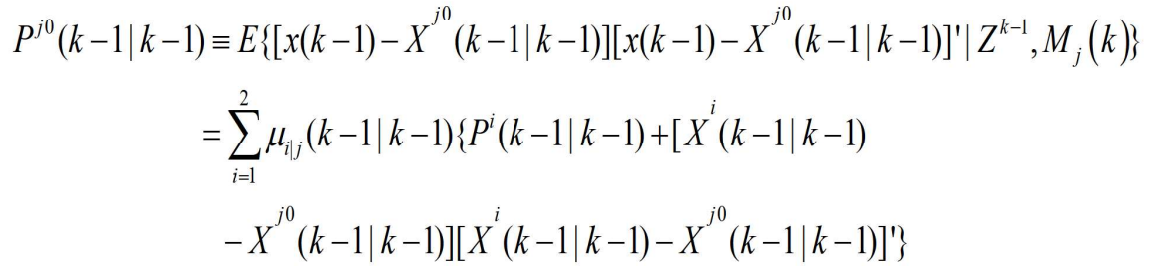
image.png

  • （2）滤波：
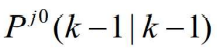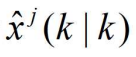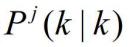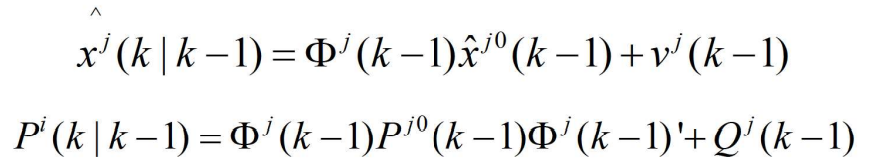
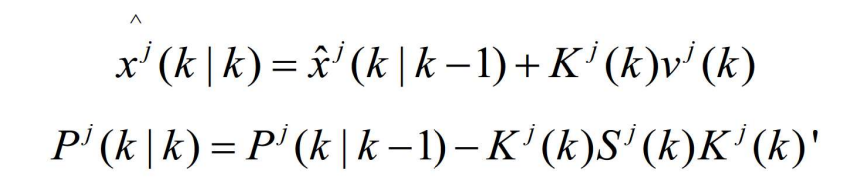
    • 基于混合初始状态估计和它的协方差image.png，应用概率数据关联算法计算 k 时刻基于模型 j 的状态估计划image.png和协方差image.png。

image.png
image.png

  • 在杂波干扰的情况下，类似于前式的证明可知，似然函数是新息的联合概率密度函数，即

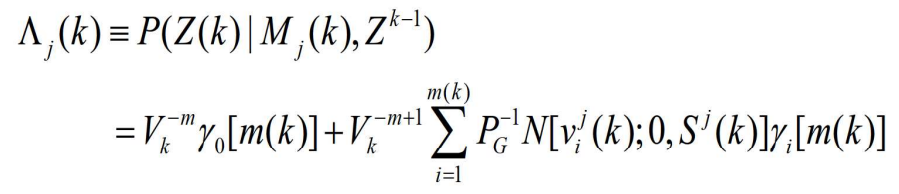
image.png

  • 其中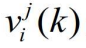，image.png是对应于量测 i 的 k 时刻的新息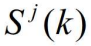，image.png是预测的量测的协方差矩阵，这两者是按模型 j 计算的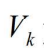，image.png是跟踪门的体积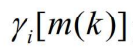，image.png是正确的量测的先验概率
    • （3）模型概率更新：
  • 多模型概率被更新为

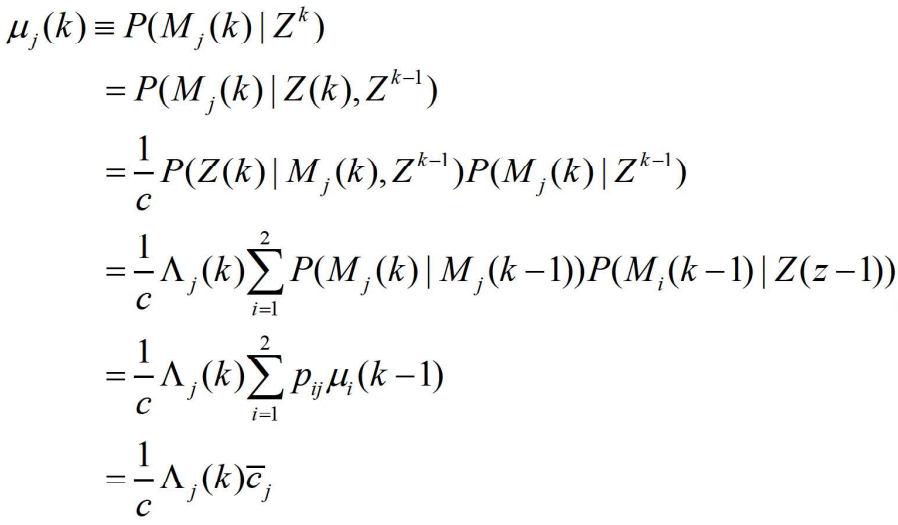
image.png

  • 其中

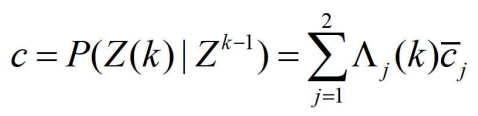
image.png

  • （4）组合：
    • 以模型为条件的估计和协方差的组合按下列方程计算：

image.png

6.3 多传感器多模型—概率数据关联滤波器

  • 多传感器多模型—概率数据关联算法是目前数据融合在目标跟踪与数据关联方面的研究中心，大部分工作都是以相互作用多模型一数据关联算法为基础的。这里我们主要介绍两传感器两模型一概率数据关联滤波器算法。

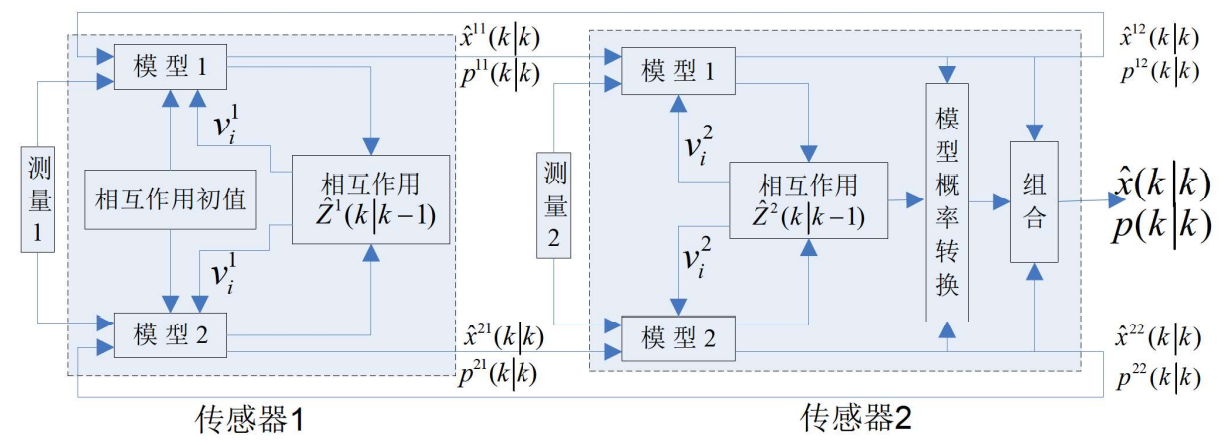
image.png

  • （1）基于前一时刻的估计混合。
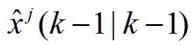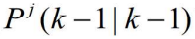    • 由image.png及协方差image.png计算与模型 j 匹配的滤波器的混合初始条件

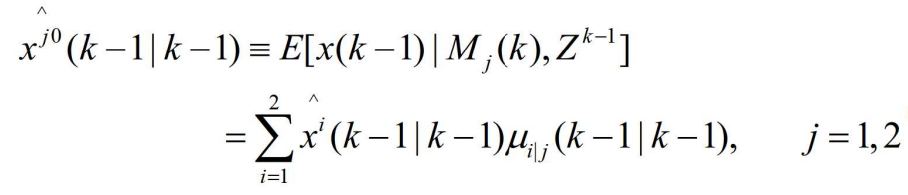
image.png

  • 其中

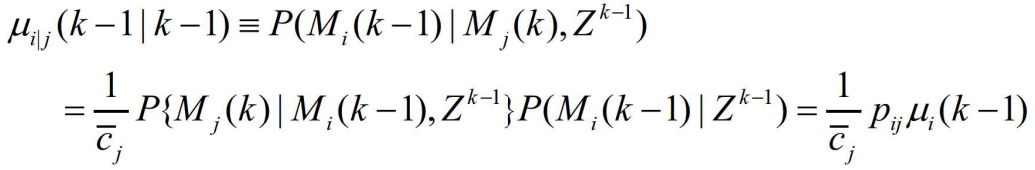
image.png

  • 其中

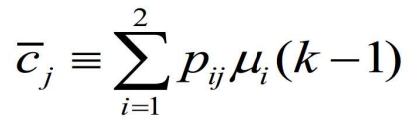
image.png

  • 是预测的模型的概率

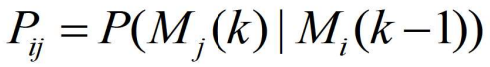
image.png

  • 是模型 i 到模型 j 的马尔可夫转移概率
  • 协方差为

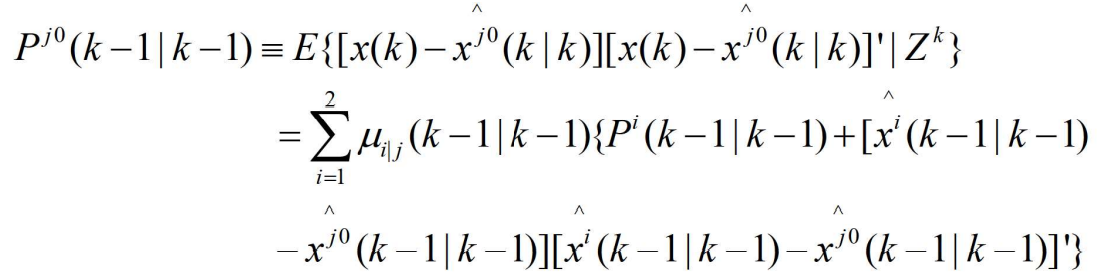
image.png

  • （2）基于混合状态估计预测状态估计和量测：

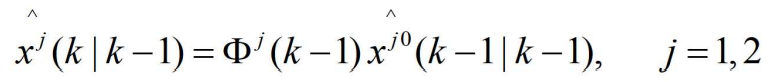
image.png

  • 它们的协方差为

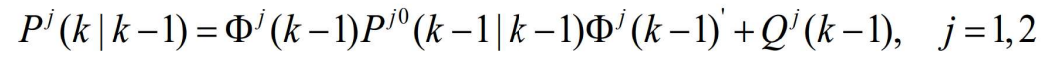
image.png

  • 对于第一个传感器:

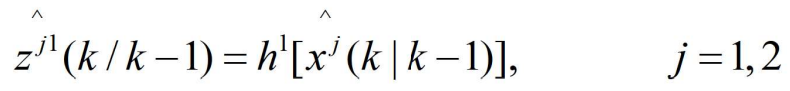
image.png

  • 它的协方差为

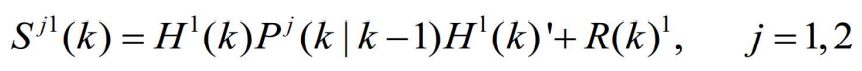
image.png

  • （3）对第一个传感器进行量测确认
    • 首先为第一个传感器以量测的预测值为中心建立跟踪门，即

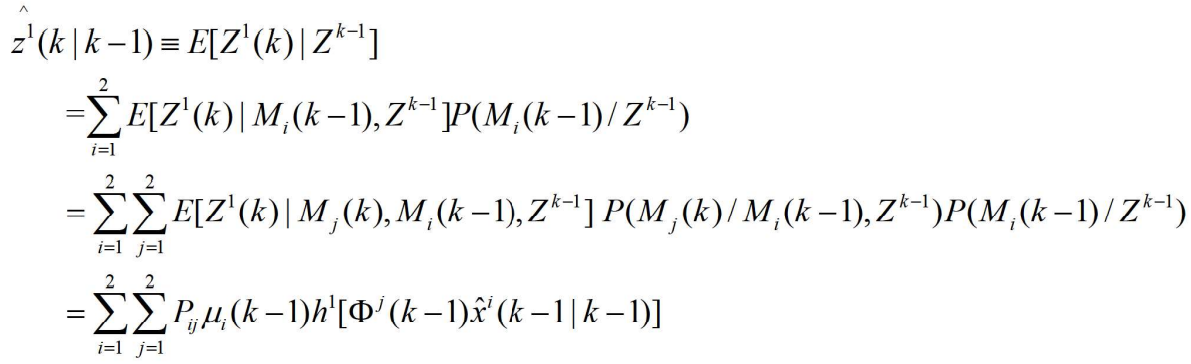
image.png

  • 对于两个模型的情形，确认区域取它们当中较大的，二维椭球确认区域的体积为

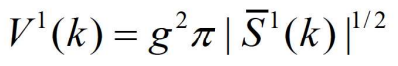
image.png

  • 其中

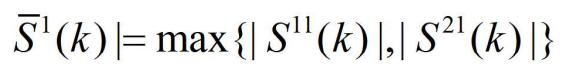
image.png

  • （4）在每一个滤波器中用第一个传感器的量测值进行估计。
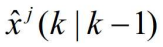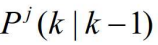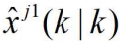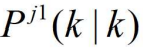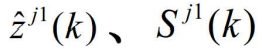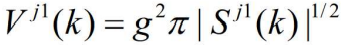    • 用image.png、 协方差image.png和来自第一个传感器的确认量测，计算image.png和它的协方差image.png。其中用image.png和体积image.png计算关联概率。和第二步相类似，由此可以导出第二个传感器预测的量测值：

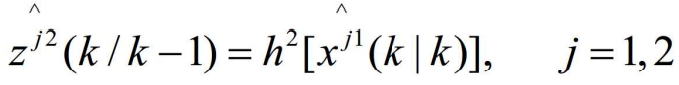
image.png

  • 和它的协方差

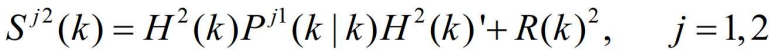
image.png

  • （5）对第二个传感器进行量测确认。和第三步相类似，首先为第二个传感器以量测的预测值为中心建立跟踪门，即

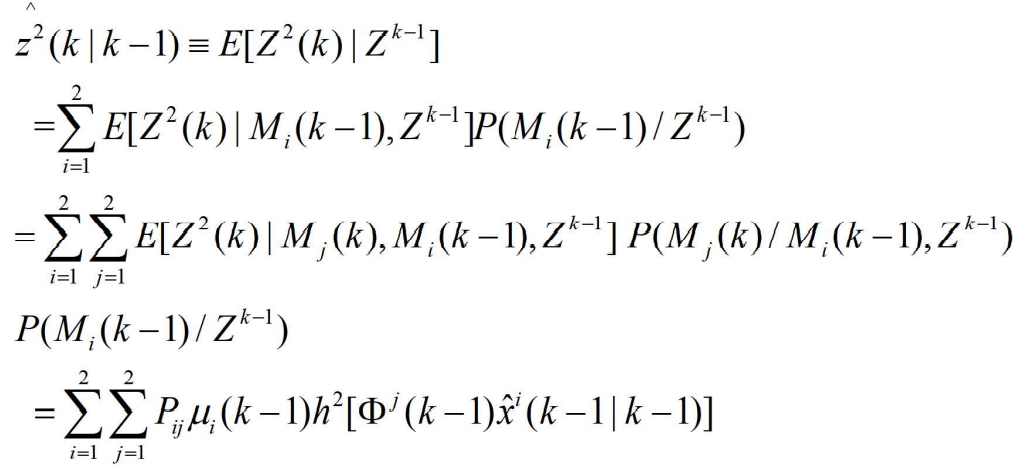
image.png

  • 对于两个模型的情形，取确认区域中较大的，二维椭球确认区域的体积为

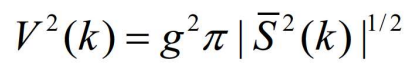
image.png

  • 其中

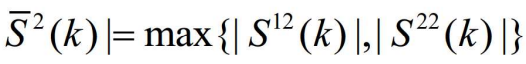
image.png

  • （6）在每一个滤波器中用第二个传感器的量测值进行估计
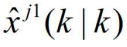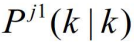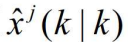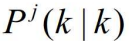
    • 从image.png和它的协方差image.png开始，用类似于第四步的方法计算image.png和image.png
  • （7）更新模型概率
    • 模型 j 在 k 时刻正确的概率可由下式计算得到：

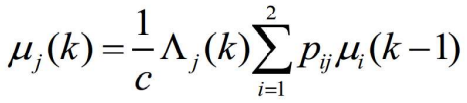
image.png

  • （8）组合
    • 以模型为条件的估计和协方差的组合按下列方程计算：

image.png
image.png