- 扩频通信系统的最大特点是具有很强的抗干扰能力
- (1)其他无线电系统发出的干扰信号,一般可以把这类干扰归类为带限平稳高斯随机过程;
- (2)多址干扰—同一扩频系统中各台站发出的干扰信号;
- (3)人为干扰—主要有窄带瞄准式干扰、宽带阻塞式干扰以及转发式干扰。
- (4)自然干扰—(如雷电、飞行体和汽车火花干扰等)归为广义平稳随机过程;
- (5)多径衰落干扰等。
衡量扩频系统抗干扰能力优劣时,通常引入“处理增益”的概念来描述。
2.1 抗广义平稳干扰的能力
2.1.1 广义平稳干扰对直接序列系统的影响
DS-SS系统模型
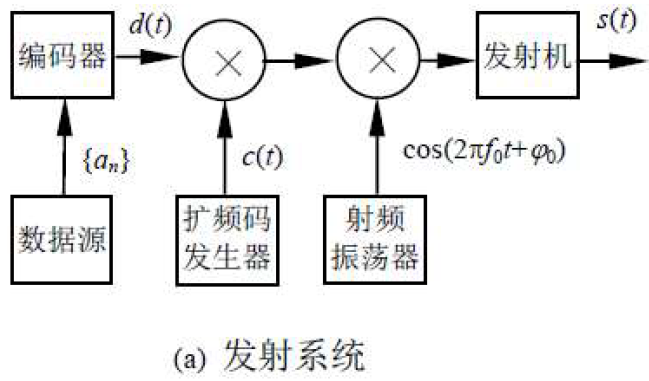
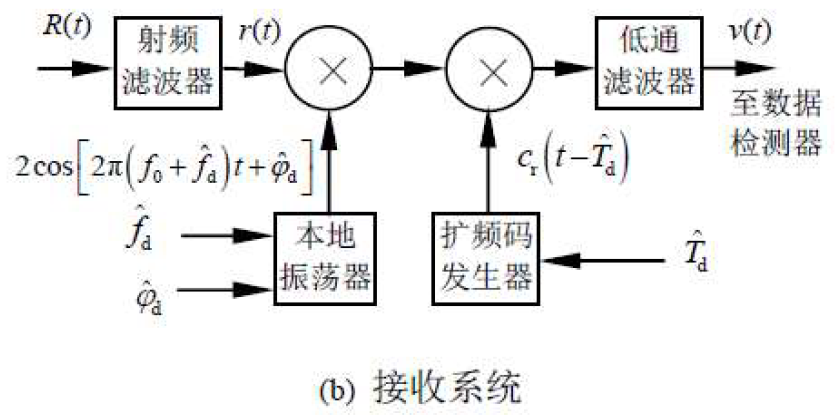
- 数学模型
- 设接收信号为:
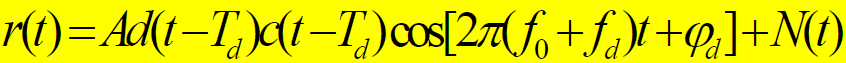
- 式中:

- 设干扰信号为广义平稳随机过程:
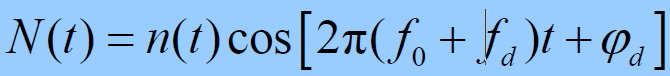
- n(t) 为基带干扰信号,均值为零的平稳高斯噪声
- N(t) 功率谱密度函数为:
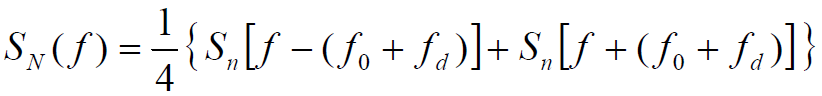
分析:干扰信号的载波与有用信号载波同频且同相送入相关器情况(最不利的情况)
输入干扰信号功率:
- 【假设】干扰信号 N(t) 的带宽不超过射频滤波器带宽
,即:n(t) 带宽
(
为扩频信号的带宽),且干扰信号 n(t) 与进入接收机的其他信号相互独立,其功率谱密度为
,平均功率(均方值)为:
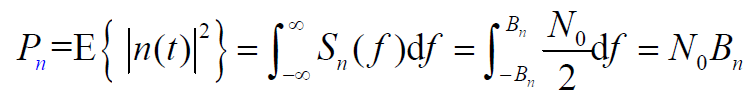
- 进入接收机干扰信号的平均功率为:
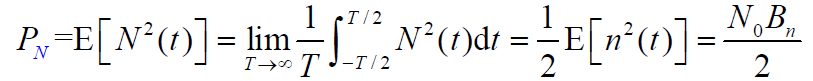
- 设基带滤波器为h(t),则干扰信号在基带(低通)滤波器的输出为:
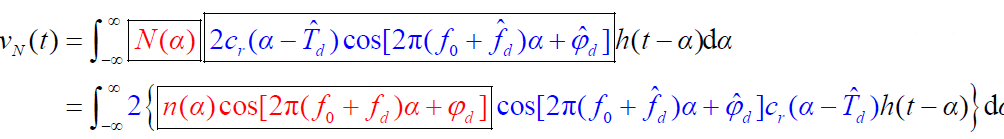
- 【假设】二次谐波被基带滤波器滤除,且系统已同步,即
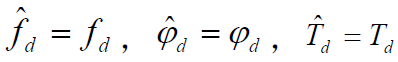
- 则有:

分析接收机输出
的统计特性:
注意:n(t) 与
相互独立
(1)
的均值(直流分量)
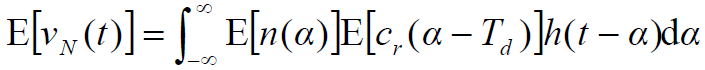
- 由于假设是零均值平稳过程,则
- (2)
的方差(交流功率)
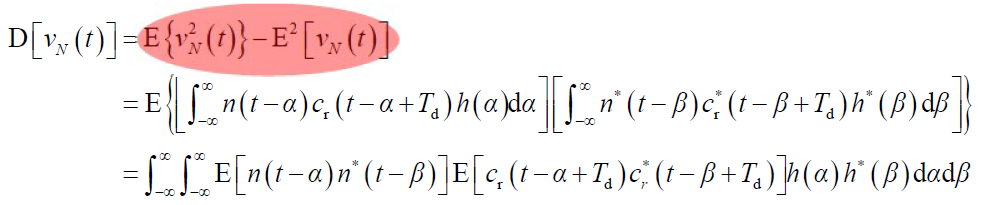
- 式中“*”表示复共轭,由于是实函数
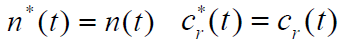
- 设 n(t) 的自相关函数为
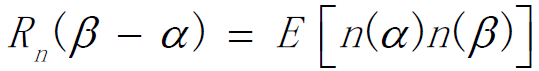
- 设的自相关函数为 
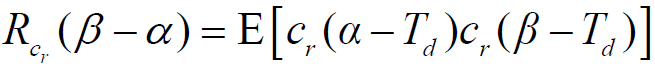
- 干扰信号 N (t) 在接收机输出的平均功率:
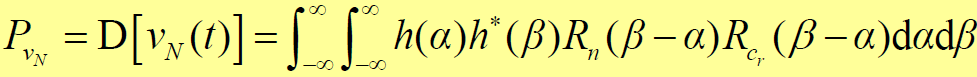
- 利用维纳-欣钦定理,有:
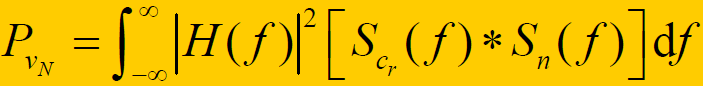
- 对干扰作用机理:广义平稳干扰功率谱密度函数由于与扩频信号的功率谱密度函数卷积而被展宽,同时又被基带滤波器的带宽所限制,从而大大降低了干扰信号 n(t) 对系统输出的影响。- 对有用信号的影响:由于信号与本地扩频码相关性很强,在卷积过程中信号能量从射频宽带内集中到基带滤波器带宽内,有用信号能量无损耗地通过低通滤波器,从而提高了系统输出信噪比。- 扩频通信系统具有强抗干扰性能的物理机理
- (3)信号的卷积过程
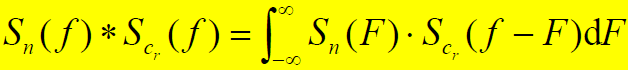
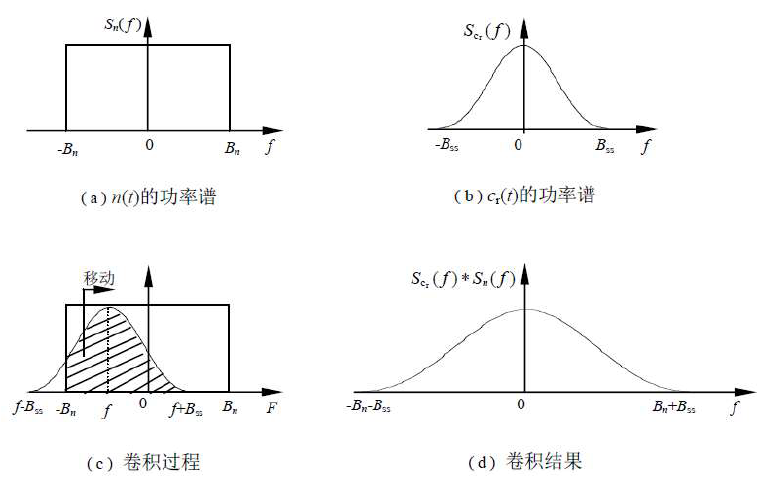
- 两信号和卷积后的带宽(单边)为
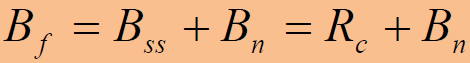
- 讨论:经过与扩频码功率谱卷积后,输入干扰信号功率谱的带宽被扩展。扩频码速率越高(的带宽越宽),干扰信号频谱的带宽被扩展得越宽,输出干扰信号功率谱的幅度就越低。- 注意:频域角度揭示了扩频通信系统抗干扰机理。当定量分析扩频系统抗干扰能力时,应用扩频系统处理增益的概念更为清楚。
- 当扩频码采用伪随机码(如m序列)时:
- 按卷积定义,系统输出噪声平均功率的表达式可表示为:
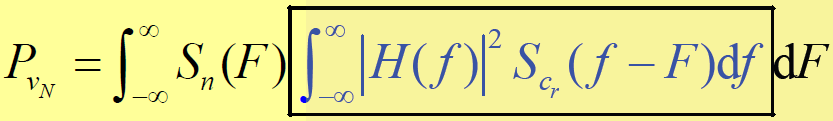
- 研究:本地扩频码通过基带滤波器后的输出功率
- 【假设】周期为N 的伪随机码(如m 序列)的码元宽度为
,振幅为1,其自相关函数为
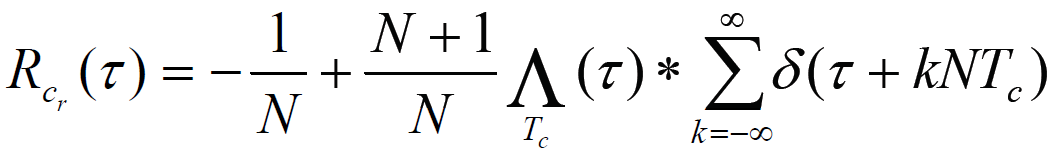
- 其中,三角脉冲函数
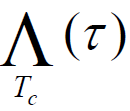 定义为:
定义为:
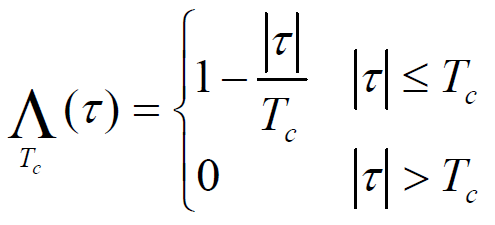
- 扩频码
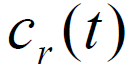 的自相关函数
的自相关函数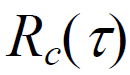 的傅立叶变换
的傅立叶变换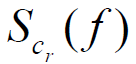 为扩频码功率谱,即
为扩频码功率谱,即
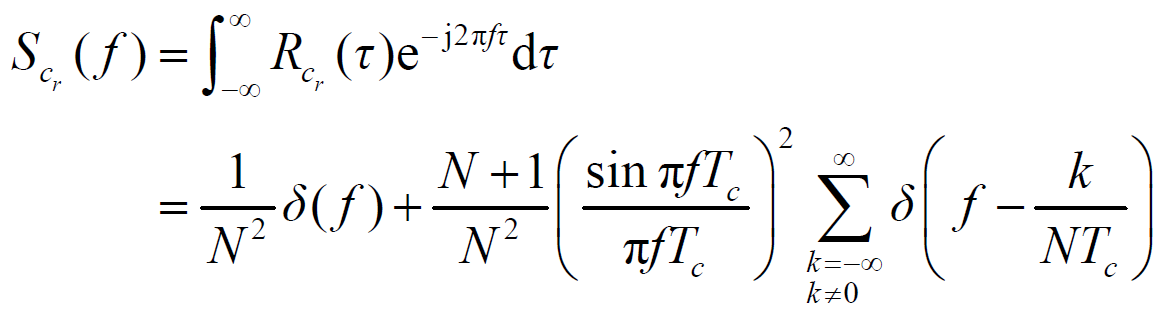
- 由于扩频码幅度为±1 ,当N→∞时,有:
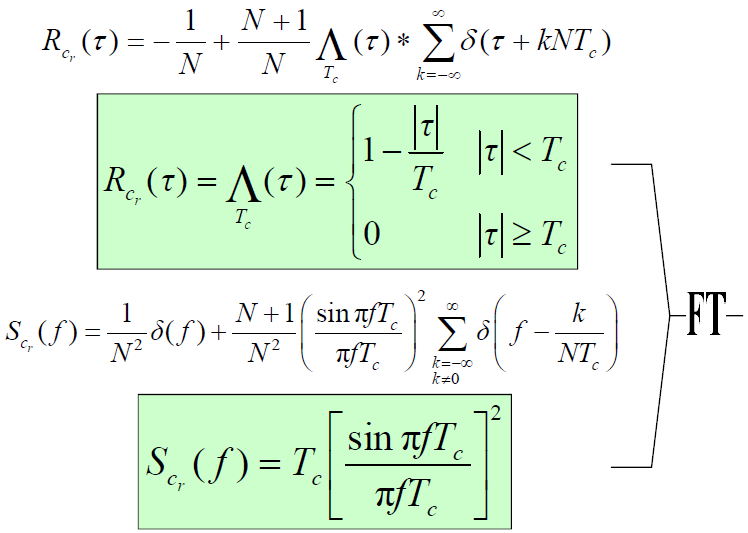
- 因为函数
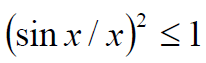 。当
。当足够大时,在基带滤波器的通频带
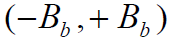 内,可以认为
内,可以认为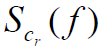 是近似平坦,可以用 f=0 处的值代替,即:
是近似平坦,可以用 f=0 处的值代替,即:
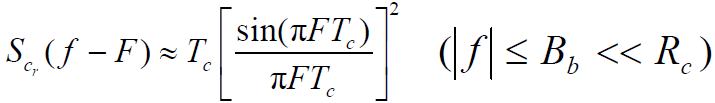
- 系统输出噪声平均功率式中的后一项积分近似处理为:
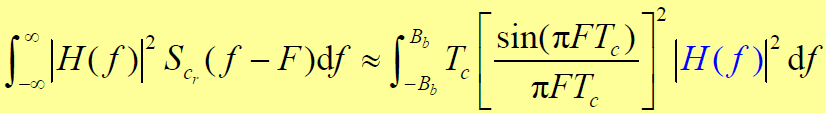
- 【假设】基带滤波器的功率传输函数是理想的,且幅频特性进行了归一化,即
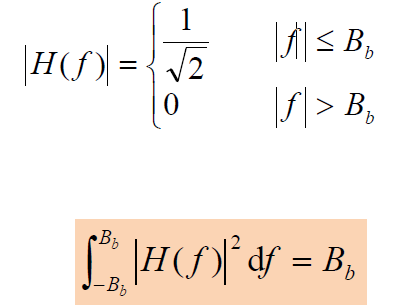
- 式表示功率传输函数曲线
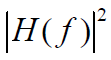 下的面积为
下的面积为 - 系统输出噪声平均功率为:
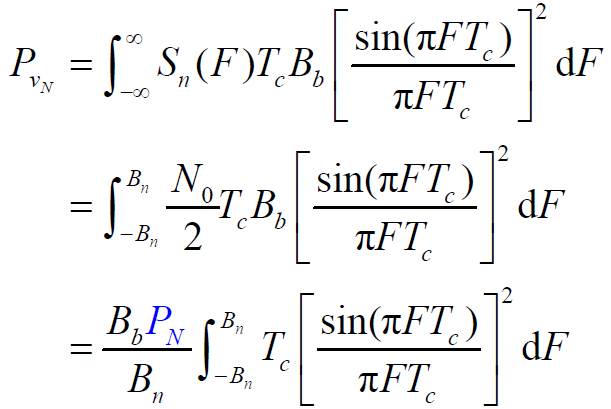
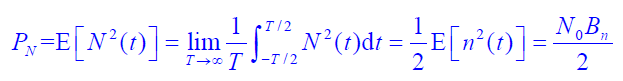
- 当干扰信号带宽
 时(
时( 为扩频码单边带宽,等于
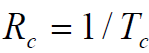 ),则输出广义平稳干扰的平均功率为
),则输出广义平稳干扰的平均功率为
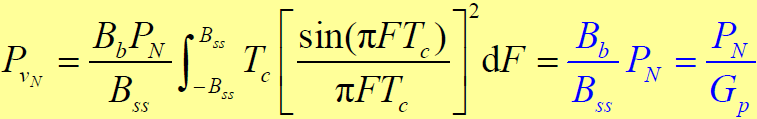
- 式中
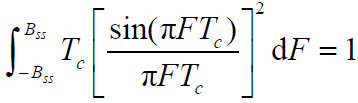 为扩频码
为扩频码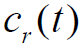 功率
功率
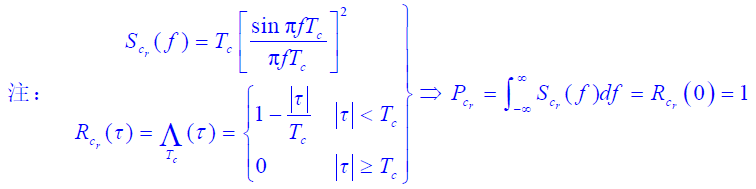
- 结论:基带滤波器输出干扰信号功率的大小与基带滤波器的带宽
成正比(为保证有用信号无失真地通过基带滤波器,取
),与扩频信号带宽
成反比。
- 通常
是
的几十倍到几千倍,所以干扰信号进入扩频接收机后一般被抑制了几十倍到几千倍
- 有用信号:相关处理过程希望有用信号的输出达到最大,即:
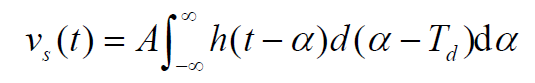
的功率谱密度函数
为
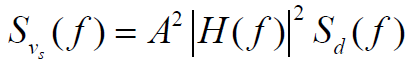
- 则,
的功率值为:
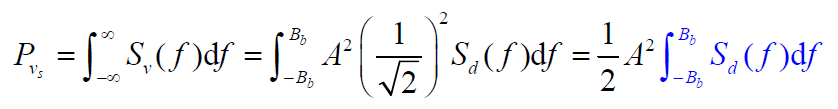
- 由于数据d(t)是等概取+1和-1的二值波形函数,
,功率值为:
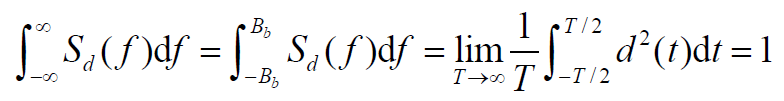
- 即:数据d(t)的功率值=1
- 则:有用信号通过扩频接收机输出功率值为
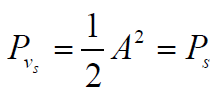
- 式中:
为有用信号输入功率
- 表明:有用信号可完全通过扩频接收机
- 干扰信号
- 干扰信号输出功率值只有输入端的
倍,被大大地抑制掉!故扩频系统的处理增益为:
- 干扰信号输出功率值只有输入端的
2.1.2 频率跳变系统抗干扰能力的分析
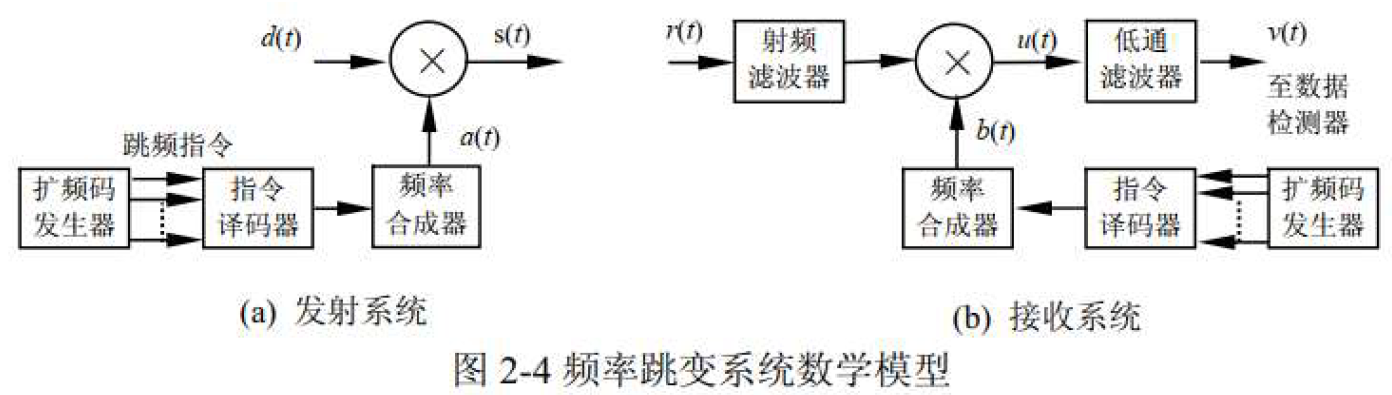
- 数学模型
- 发射机输出信号为:
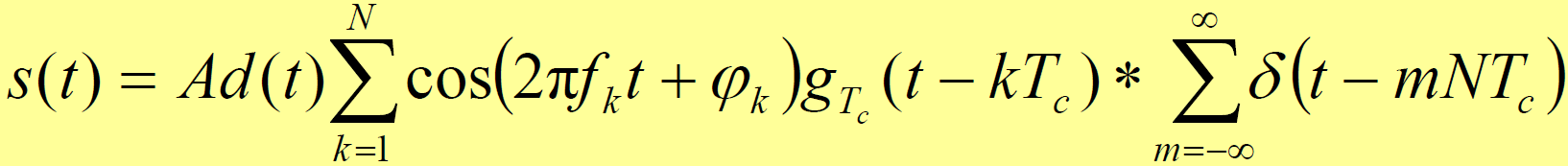
- 接收信号为(忽略传输损耗):
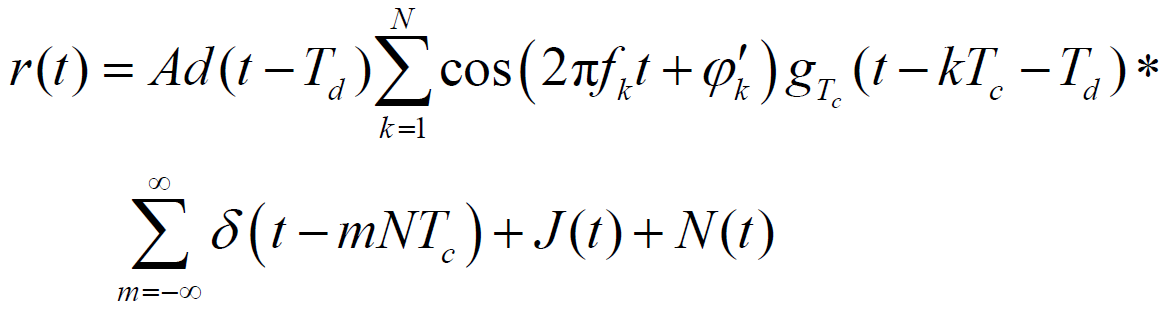
- 接收机本地信号为:
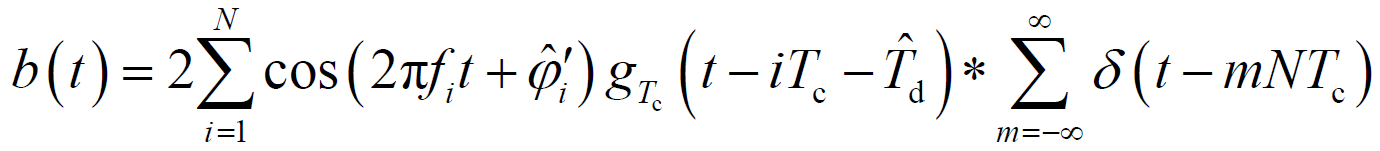
- 【假设】
- (1) 进入接收机的干扰信号为J (t),其功率
均匀分布在整个扩频通带
内
- (2) 广义平稳干扰N(t)可以归入J (t)中,不再单独考虑N(t)对跳频系统的影响
- 干扰信号模型
- FH-SS,射频通带被分割成N个频道,中心频率分别为f1,f2,…,fk,…fN
- 将带通干扰J(t)分解为:N个子信号
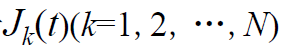 ,
,的中心频率分别为fk (k=1,2, …,N) ,带宽为
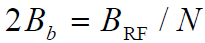 。
。
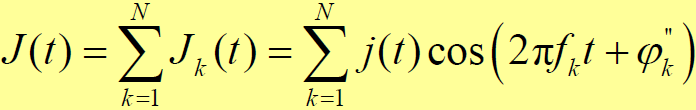
- 其中,j(t)是带宽为
的低通信号,均值为0,功率为
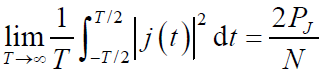
- j(t)功率谱密度:
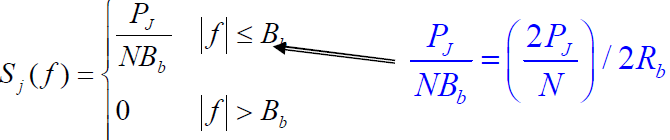
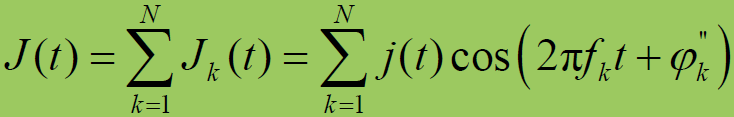
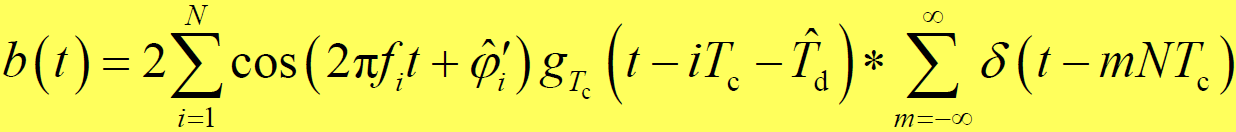
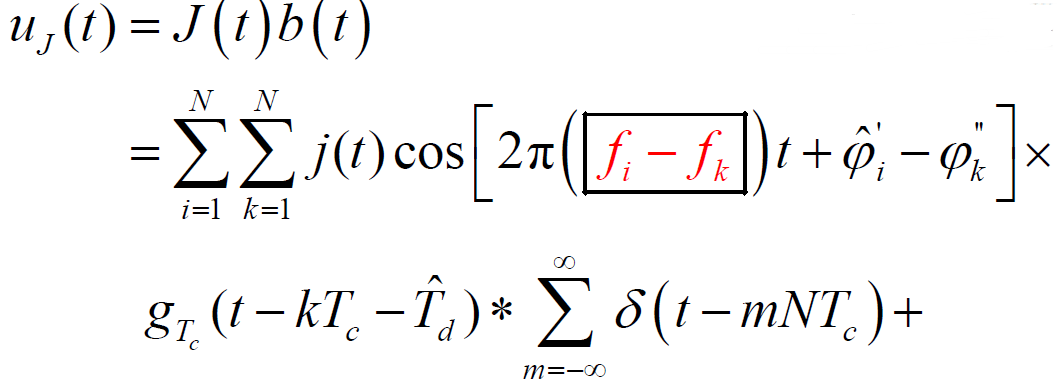
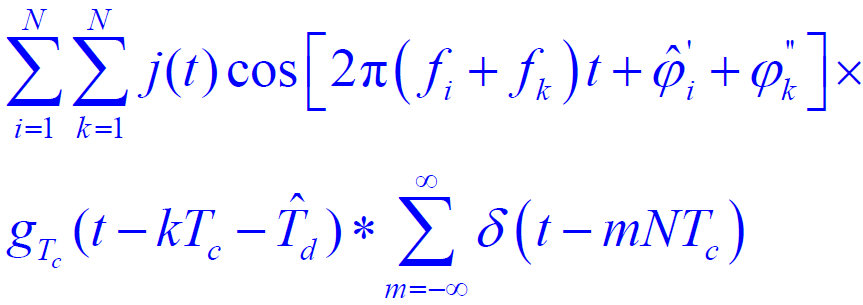
- 讨论:
- (1)第二项:落在低通频滤波器通带之外
- (2)第一项:只有
的分量能通过低通滤波器
- 故:干扰信号通过低通滤波器后的输出:
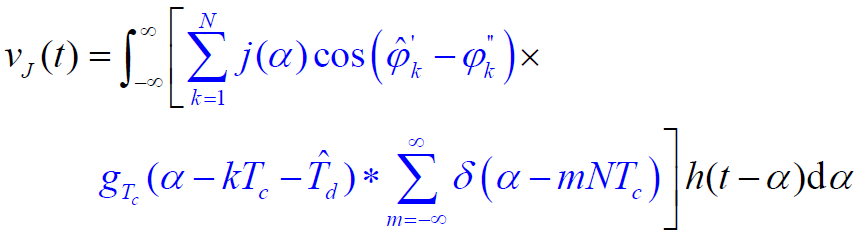
- 【假设】系统已取得同步
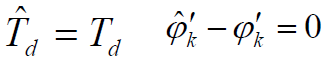
- 由于
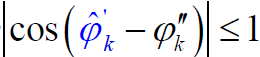 ,取其最大值,即干扰信号与有用信号同相进入接收机(即干扰信号通过接收机后有最大的输出,干扰最为严重的情况),有:
,取其最大值,即干扰信号与有用信号同相进入接收机(即干扰信号通过接收机后有最大的输出,干扰最为严重的情况),有:
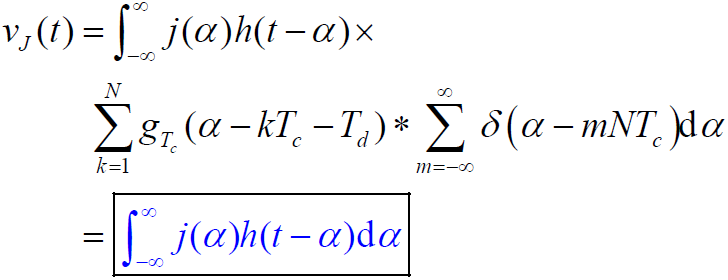
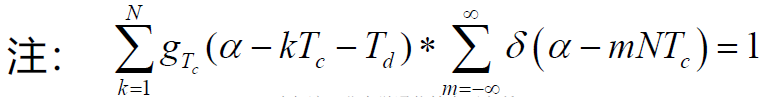
- 假设系统是线性的,可以用叠加定理分别对干扰信号与有用信号进行分析,则低通滤波器的输出为:
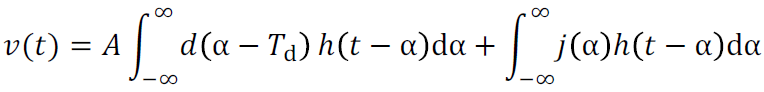
- 低通滤波器滤波后干扰信号的功率谱密度函数为:
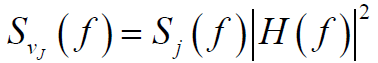

- 通过低通滤波器后,干扰信号与噪声的功率为:
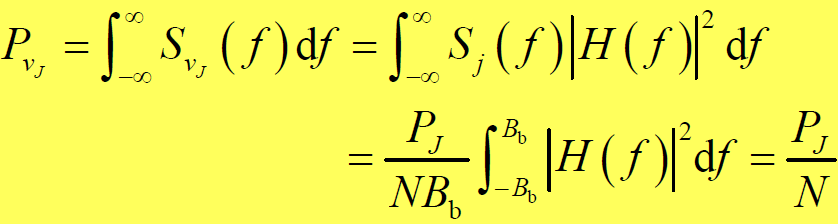
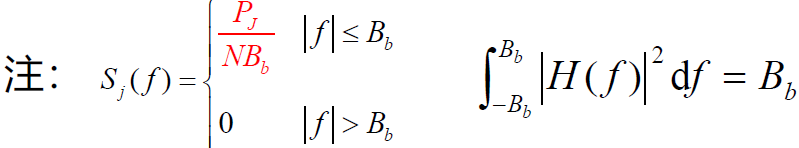
- 讨论:干扰信号功率被消弱了N倍。因此输出信号噪声(干扰)功率比与输入信号噪声(干扰)功率比的比值(处理增益)为
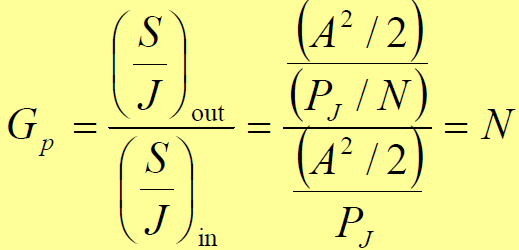
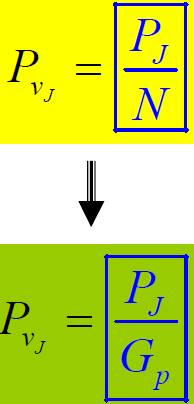
- FH系统抗窄带干扰的物理本质
- 系统同步后,只有当跳频信号跳变到受到干扰的那个频道时,此窄带干扰信号才能通过低通滤波器。
- 由于在
时间内,跳频信号在每个频道的工作时间为
- 在其他的
时间内,由于本振信号频率的变化,干扰信号通过混频后,其频谱落在了低通滤波器的通带之外,被低通滤波器滤除了
- 通过接收机的解跳,干扰信号功率通过低通滤波器后被消弱了N倍
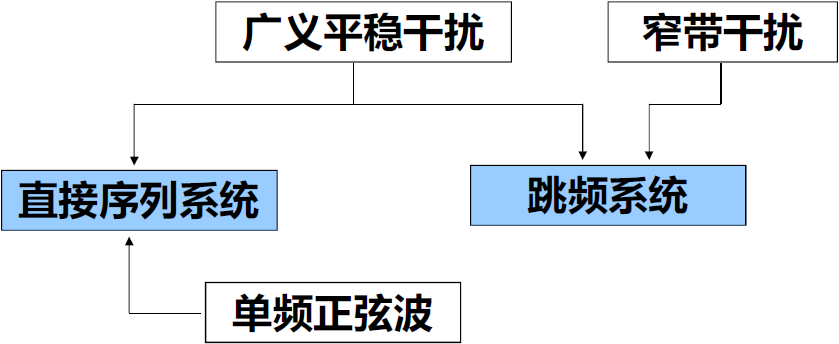
- FH系统抗宽带干扰和窄带干扰的机理
- 干扰信号模型
- 单频正弦波干扰是一类特殊干扰,可作为带宽
的窄带干扰来处理
- 单频正弦干扰信号J (t)与有用信号是相互独立的,且与有用信号的载波同频、同相。
- 在这种假设条件下,单频正弦波干扰实际上是一种窄带瞄准式干扰,表示为:
- 单频正弦波干扰是一类特殊干扰,可作为带宽
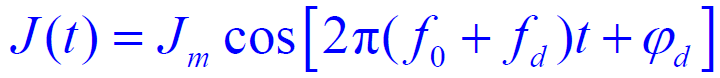
- 系统对干扰信号的响应
- 经过相关处理后,基带滤波器输出端的响应为
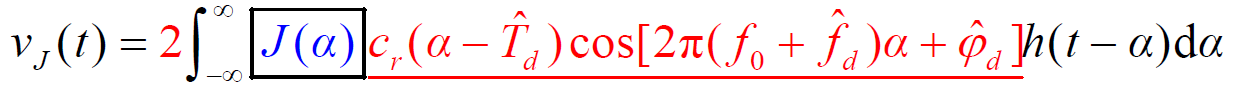
- 系统同步,输出干扰信号为:
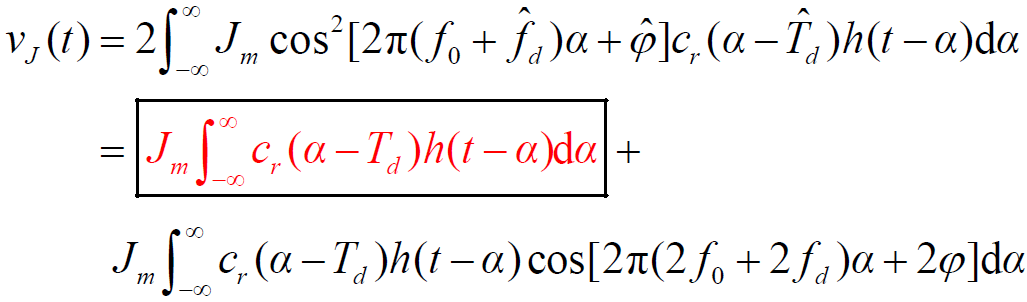
- 滤除二次谐波,输出干扰信号为:
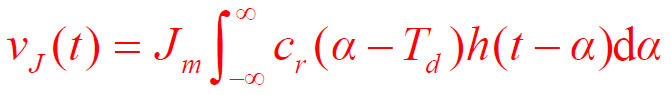
功率谱密度函数:
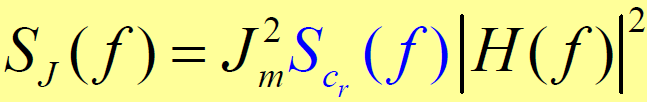
- 【假设】对于理想扩频码(1 和0 出现的概率各为1/2,幅度为1,周期N 为无限长),则
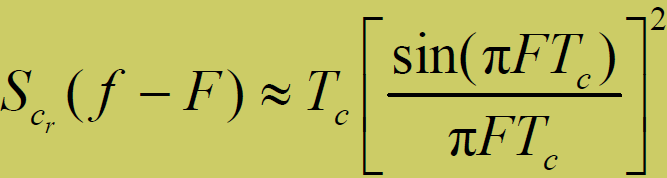
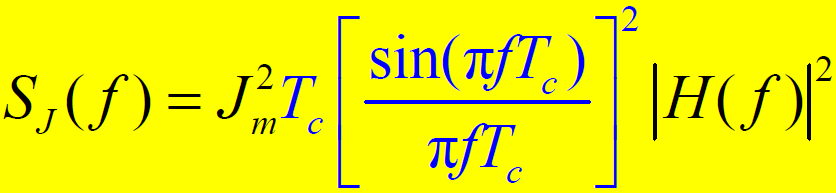
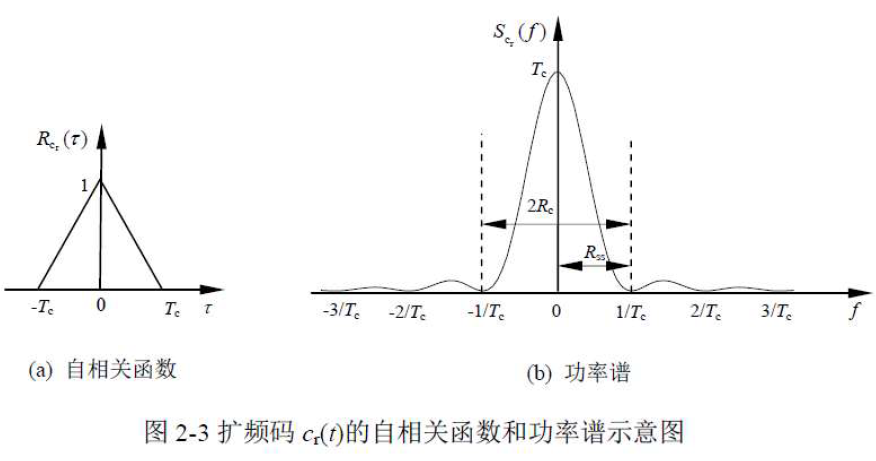
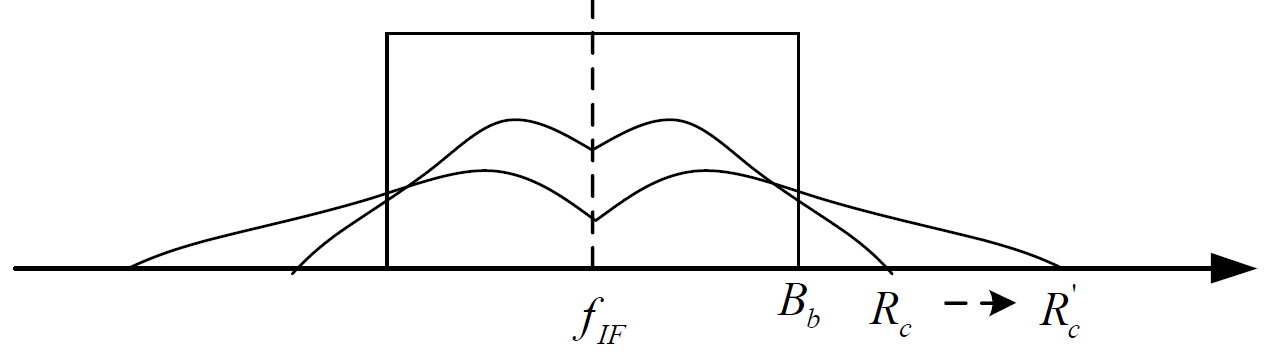
- 扩频码功率谱:幅度的最大值在
处,且为
。当扩频码的码元宽度
减小时,扩频码功率谱幅度的最大值将减小,频谱宽度将增大,功率谱被展宽且趋于平坦
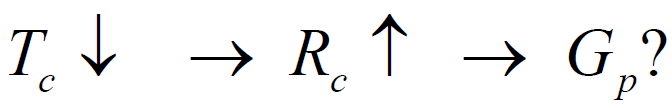
- 讨论:单频正弦干扰信号经过接收机的相关处理,再经过基带滤波器的滤波,输出的功率随着扩频码码元宽度
的减小而减小。
- 单频正弦干扰信号输出功率:
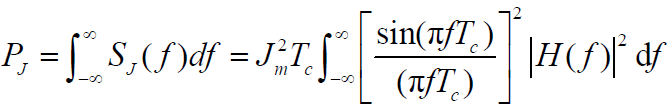
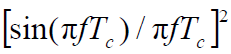 带宽远大于H( f )带宽,在H( f )通频带内,可近似为1,即
带宽远大于H( f )带宽,在H( f )通频带内,可近似为1,即
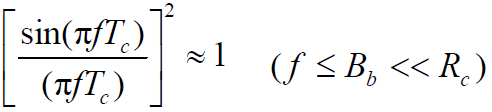
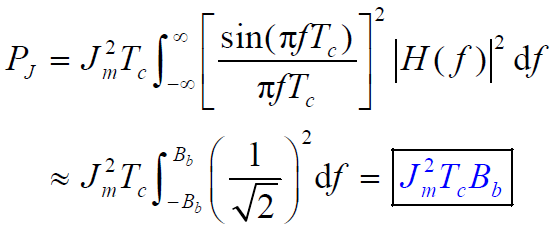
- 单频正弦干扰信号的输入功率为
,信号功率为
,即
。理想相关器情况下有:
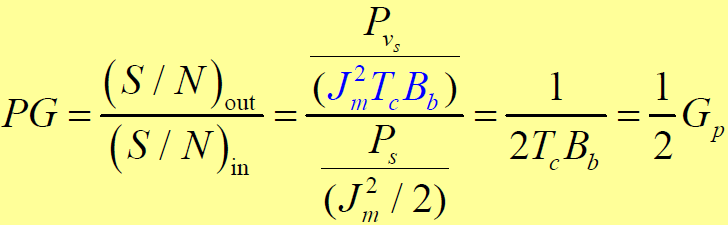
- 系统处理增益降低了
- 讨论:与载波同频同相的单频正弦干扰和广义平稳干扰对系统的影响是不同的

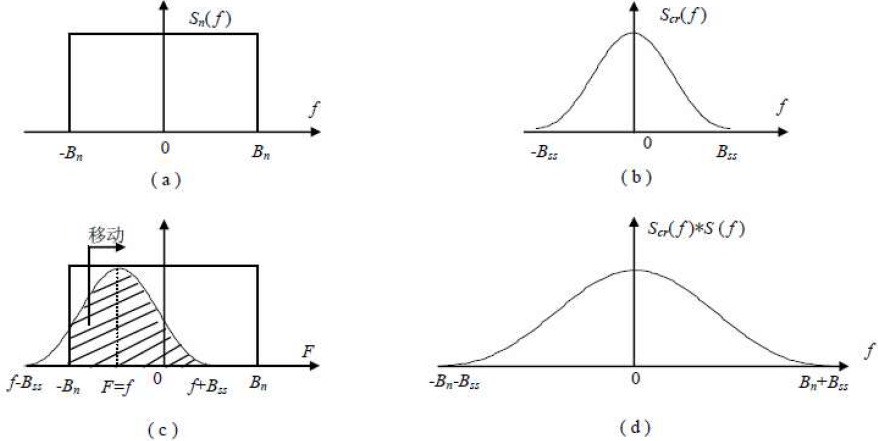
实质:接收机对带宽为
的干扰信号相关解扩的过程,实质是本地参考扩频码对干扰信号进行频谱扩展的过程,相关解扩后干扰信号的带宽被扩展为
。
带宽:
- 在干扰信号功率不变的情况下,相关解扩后,宽带干扰信号的带宽被扩展成为
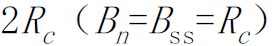 ,而单频正弦波干扰信号的带宽被扩展成为
,而单频正弦波干扰信号的带宽被扩展成为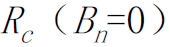
- 在干扰信号功率不变的情况下,相关解扩后,宽带干扰信号的带宽被扩展成为
- 功率谱:
- 电波传播由于不同长度的路径,引起不同传播时延,各路信号叠加,将产生频率选择性衰落现象,使信号产生严重失真和波形展宽,使通信系统发生严重的误码甚至通信中断。多径干扰是乘性干扰。
- 双波束模型
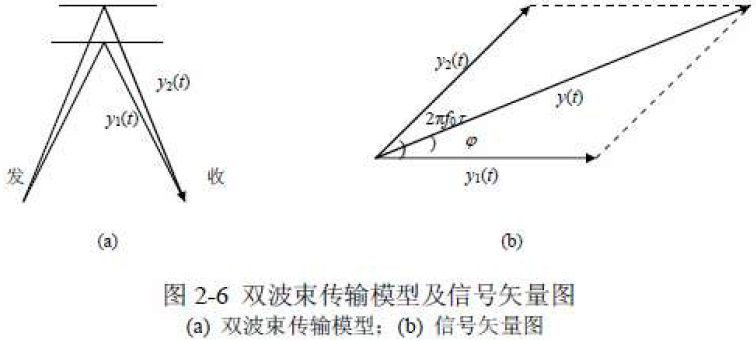
- 【假设】两传播路径的传输系数相同,仅路程不同
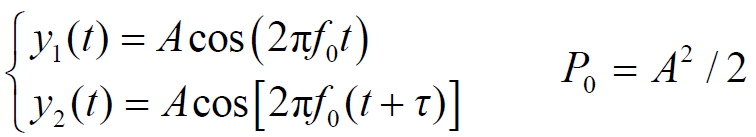
- 合成信号:
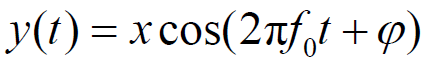
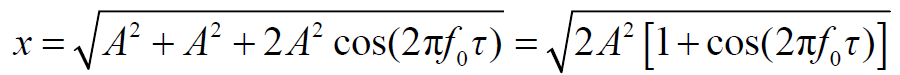
- 合成信号功率:
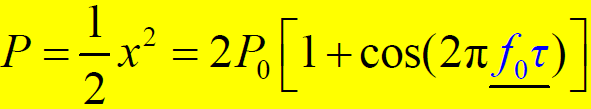
- 当
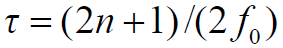 (n 为正整数),
(n 为正整数),,通信中断
- 衰落会降低有用信号功率,从而增加干扰的影响,使接收信号产生失真、波形展宽、波形重叠和畸变,甚至造成通信系统解调器输出出现大量差错,以至完全不能通信。
- 克服多径衰落常用的方法是采用分集技术。通过选择工作时间、工作频率或接收点的位置,使得
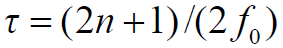 不能成立,即所谓的时间分集、频率分集或空间分集。
不能成立,即所谓的时间分集、频率分集或空间分集。 移动通信系统,采用分集、均衡和信道编码技术来改进接收信号质量,既可单独使用,也可组合使用
2.2.2 双波束信号对直接序列系统的影响
情况1:白噪声
- 香农指出:在高斯信道上,传输的最佳信号形式是具有白噪声统计特性的信号情形
- 合成信号
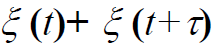
- 合成信号功率:
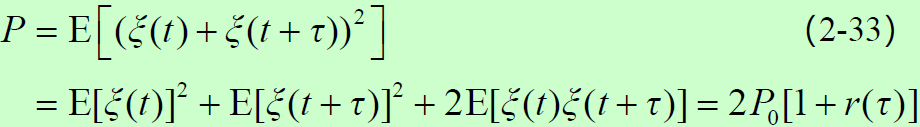
- 归一化自相关函数
- 高斯白噪声自相关函数具有
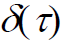 函数形式
函数形式
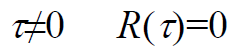
- 合成信号功率:
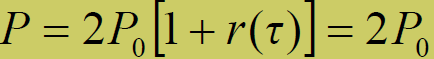
- 结论:利用具有高斯白噪声统计特性信号传送信息,当τ≠0时,r(τ)都为零,即这种通信系统不会发生干涉衰落,接收信号平均功率因为没有干涉现象而恒定不变。抗多径干扰的理想系统
- 由于无理想的高斯白噪声信号,理论上的极限值
- 情况2:带限白噪声
- 带限白噪声功率谱密度:
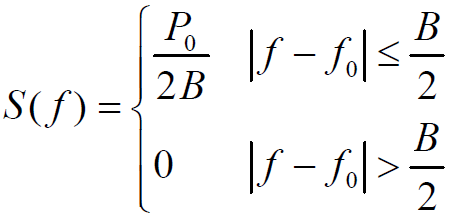

- 自相关函数:
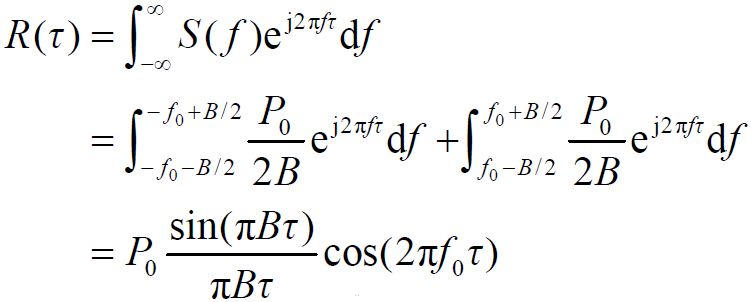
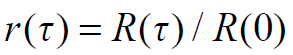
- 则有:
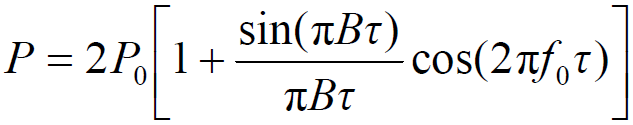
- 接收信号功率的相对起伏为:
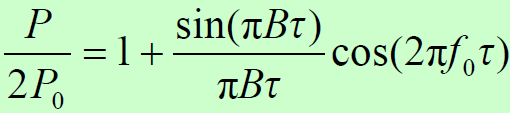
- 由于
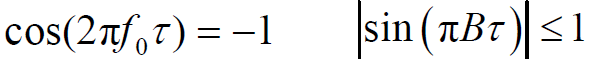
- 近似后得:
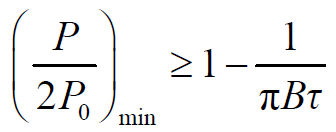
- 讨论:只要系统带宽B足够大,就可使接收信号功率最小的相对起伏
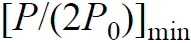 任意地接近1。即:可以通过增加系统的带宽,从根本上消除多径衰落现象。
任意地接近1。即:可以通过增加系统的带宽,从根本上消除多径衰落现象。 通过增加系统带宽,可从本质上消除多径衰落现象
【例如】假定要求
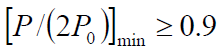 ,则有
,则有
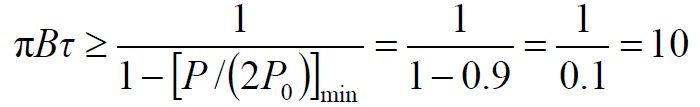
- 只要选择系统的带宽满足
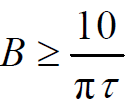
- 就可保证接收信号功率的相对起伏不会超过10%
- 统计表明,在1500km以上的短波线路上,τ<0.2ms 的情况是很少见的,一般都在0.2ms≤ τ ≤2ms范围,因此
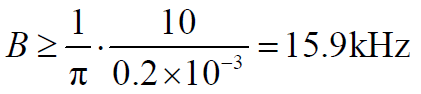
- 用带宽为16kHz的带限白噪声信号在短波线路上传送信息时,收到的合成信号功率(两波束场合)起伏不会超过10%
- 注意:一些文献1/ τ将定义为传输系统(或信道)的相干带宽( coherence bandwith ) , 或称相关带宽( correlation bandwith)。当信号的带宽大于传输系统的相干带宽时,将产生频率选择性衰落,引起符号间的干扰(intersymbol interference,ISI)。
- 情况3:伪噪声码
- 扩频系统使用PRN来逼近白噪声信号统计特性
- 当伪噪声码周期N足够长,具有与白噪声相类似的自相关函数:
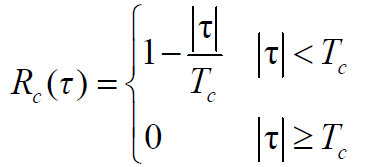
- DS-SS系统中,载荷信息的载波不再是一单频正弦波,而是一受扩频伪随机码调制的近似于带限白噪声的信号:
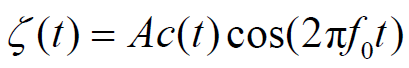
- 接收到的两路信号分别为
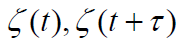
- 合成信号功率:
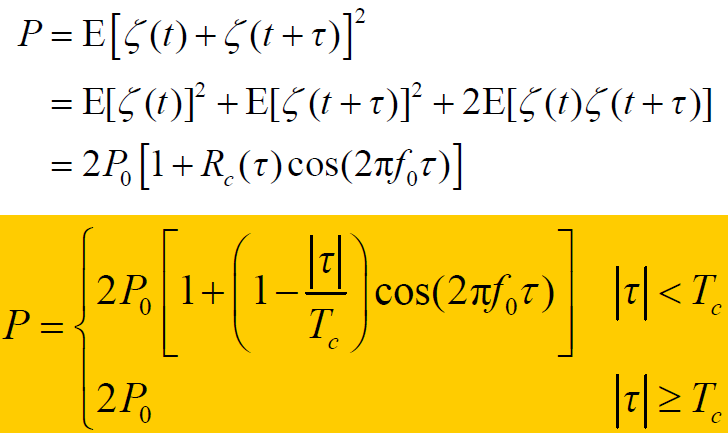
- 讨论:伪随机码尖锐的相关特性使多径波束完全独立
- 信号模型
- 发射信号:
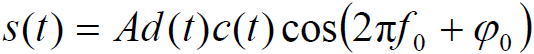
- 接收信号:
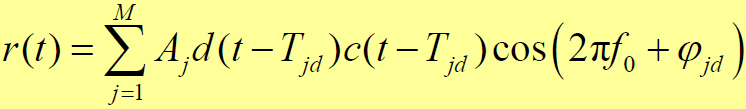
- 其中:Aj 为第 j 径电波的幅度,
为第 j 径电波的传播延迟,
为第 j 径电波的载波相移,j=1 时的信号是所需要接收的信号,j=2,…,M 时的信号为多径干扰信号
- 【假设】系统已经同步,即
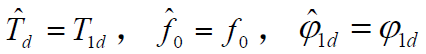 ,接收机本振信号为:
,接收机本振信号为:
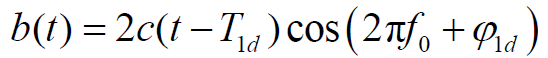
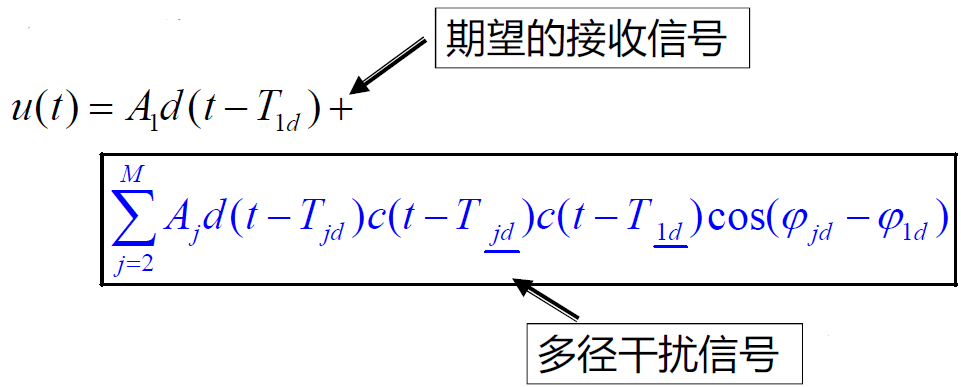
- 混频器输出:
- 干扰信号响应
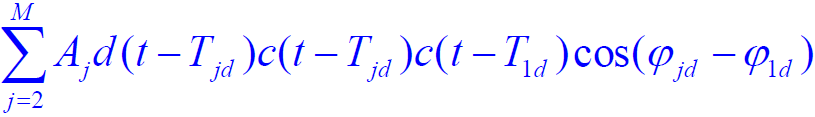
- 第二项中
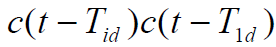 的高频分量不能通过低通滤波器,其低频分量为:
的高频分量不能通过低通滤波器,其低频分量为:
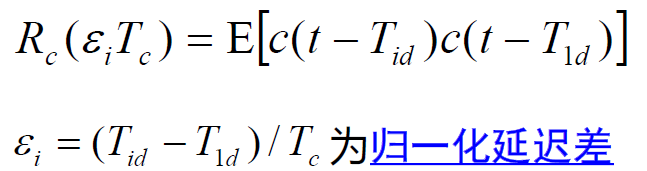
- 令
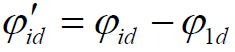
- 则多径干扰信号通过低通滤波器的输出为:
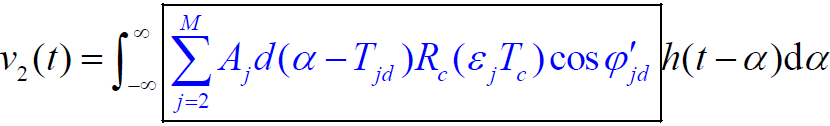
- 设
在
上均匀分布

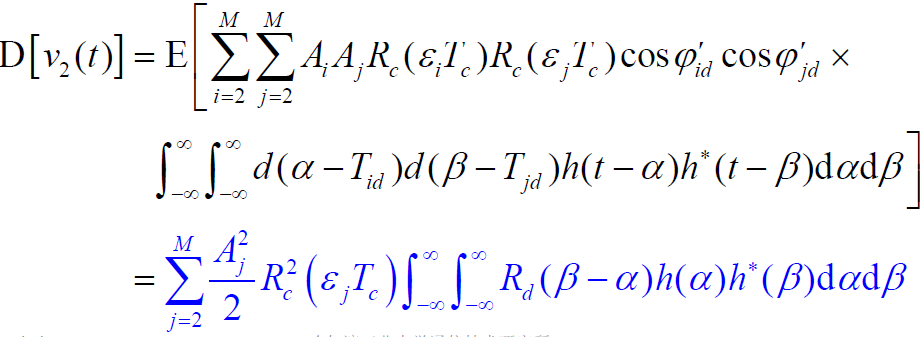
- 频域可表示为:

- 讨论:
- (1)当
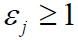 时,
时, 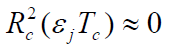 (当扩频码长度 N 足够长时),到达接收机的多径信号通过相关解扩时,被作为随机干扰抑制掉
(当扩频码长度 N 足够长时),到达接收机的多径信号通过相关解扩时,被作为随机干扰抑制掉 - (2)当
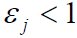 时,
时,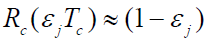 ,因而有
,因而有
- (1)当
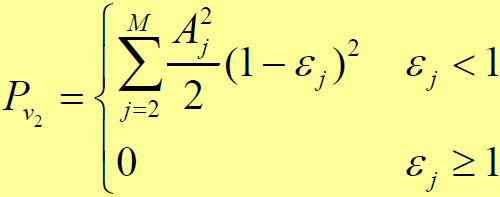
- 由于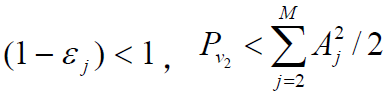,多径干扰影响减轻- 频率跳变系统也可得到相似结论,它与直扩系统抗多径干扰的能力完全相同
DS-SS:
码分多址(Code Division Multiple Access,CDMA)由扩频理论和技术引出,完全不同于FDMA和TDMA。
特点:
- (1)把所有频率资源和时间资源全部分配给同时接受服务的用户,每个用户输出功率需控制在达到最低性能要求的信噪比上。每个用户可任意长时间占有整个给定频带。
- (2)影响所有用户的背景干扰和噪声来自每一个用户,即码分多址扩频系统是一种自扰系统。
- (3)蜂窝系统中,其通信容量比FDMA和TDMA的容量要大得多。
CDMA系统中,每一个用户对其他用户而言都是干扰,影响系统用户总数主要因素是系统内多址信号的干扰
- 【分析孤立系统内的多址干扰情况】
- 【假设】
- 信道:高斯白噪声信道
- 系统:M个用户,每个用户输出功率受控,基站接收到的所有用户功率都相等(功率控制)
- 基站接收信号:
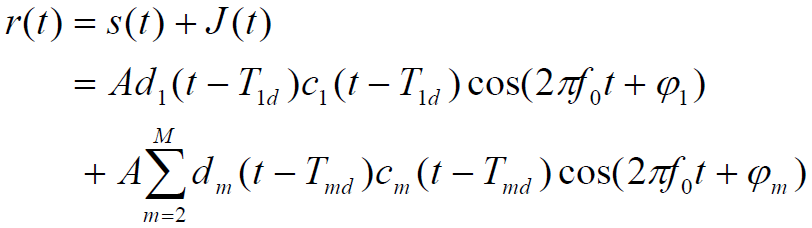
- 第1个用户为有用信号:
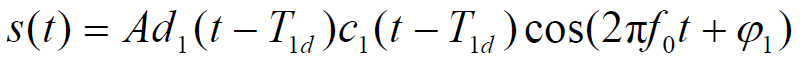
- 多址干扰信号:
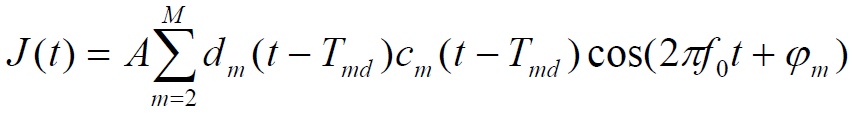
- 【假设】基站已与用户1取得同步,即
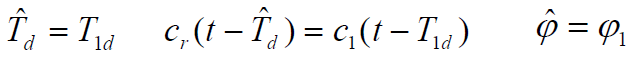
- 基站相关器输出用户1的信号:
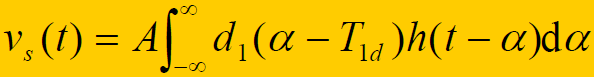
- 其他多址干扰信号通过相关器后为:
2.3.1 多址干扰对直接序列系统的影响
- 由于低通滤波器频带窄,
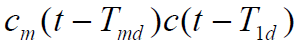 中只有低频分量与
中只有低频分量与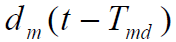 频谱卷积才能通过
频谱卷积才能通过
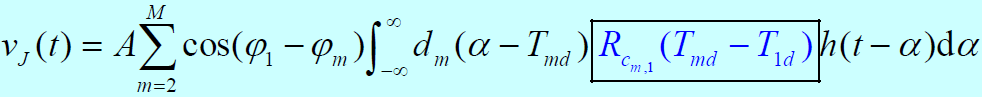
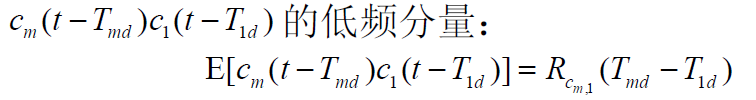
- 若系统使用扩频码较理想,自相关特性尖锐,互相关特性近似为零
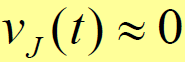
- 理论上,具有尖锐自相关特性同时又具有理想互相关特性的扩频码不存在,因而多址干扰在相关器后的输出不可能为零
- 求解
功率:


- 原因同:

- 【假设:若系统扩频码使用m序列】
- 长度为N的m序列码互相关函数的均值和方差为:
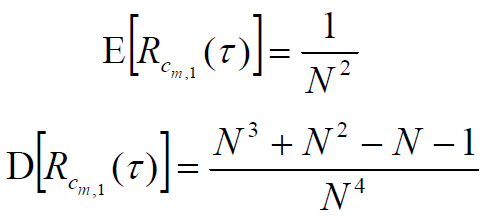
- 则有:
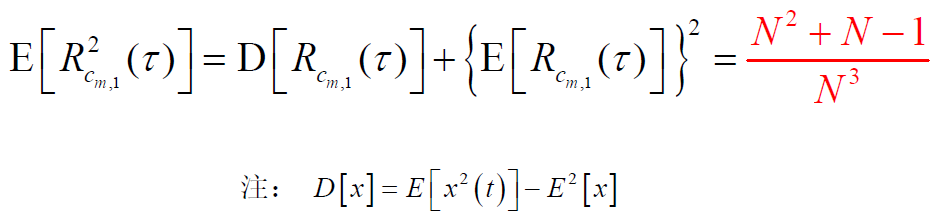
- 在N较大时
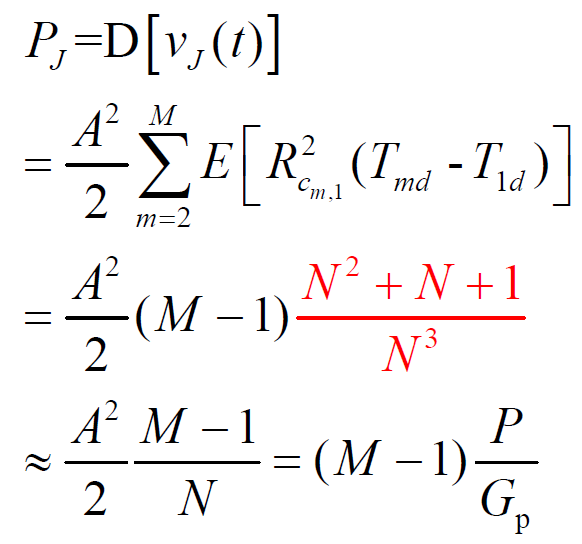
- 因此得到
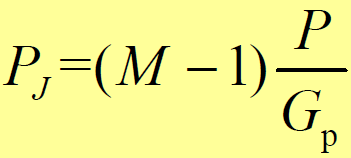
讨论:
CDMA容量
- 【假设】系统由一个基站和M个用户组成
- 其他 M-1 个用户的多址干扰,可等效为 M-1 个平稳干扰源。基站接收到M 1个用户的多址干扰功率:

- 【假设】多址干扰功率均匀分布在解扩后全部信号带宽内,则:
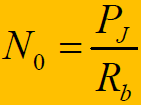
- 由于
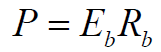
- 则有
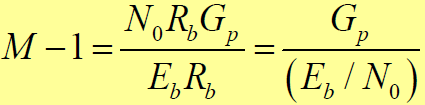
- 式中,
为基站解调器的品质因素
- CDMA 系统用户数与解调器要求的
之间的关系
CDMA 系统中, 用户容量 M 和扩频处理增益
成正比(当M >> 1时),即系统内的用户数量随着系统扩频处理增益的增大而增加,等于干扰容限
CDMA系统实际容量
实际系统中有两个因素应当考虑:
(1)蜂窝CDMA 系统,必须要考虑其他小区用户对本小区用户的干扰
- 理论研究与经验表明:若所有用户均匀分布在每个小区中,且基站能恰当地控制用户发送功率,则所有其他小区产生干扰总和大约是本小区中所有其他用户产生干扰的3 / 5倍,用相对干扰因子表示:

- (2) 当话音(或数据)停顿或减小时,常采用停止传送或降低传输速率或功率
- 对于均匀分布的用户,可减少用户平均输出功率,从而减小每个用户所受干扰。只要用户总数足够大,大数定理表明:干扰在大多数情况下将保持在均值附近。
- 系统用户容量随着总的传送速率的减小而成正比例地增大。这一比率称为话音激化增益
。
通话统计数据证实:话音活动只占全部通话时间的3/ 8,即
相对干扰因子ξ影响:系统用户容量降低
倍
话音激化增益Gp影响:系统用户容量增大
倍
系统用户容量修正为:
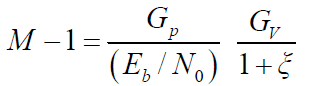
- 当M >> 1,可简化为:
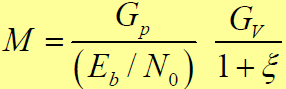
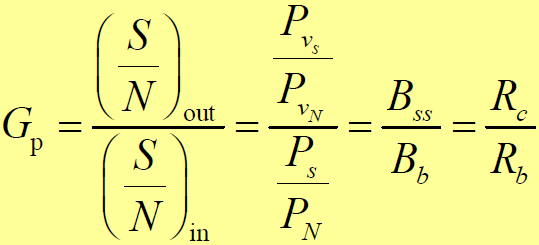
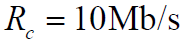 ,即
,即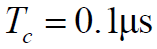 时,反射路径时延小于直接路径时延
时,反射路径时延小于直接路径时延