整数规划问题

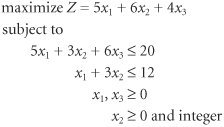
整数规划，或者离散优化（Discrete Optimization）
是指数学规划（Math Programming）问题中自变量存在整数的一类问题
上面这个数学规划问题，便是一个混合整数线性规划问题
首先目标方程和约束方程都是线性的，其次自变量既有连续变量（x1、x3），又有整数变量（x2）

与线性规划连续的可行域（可行解组成的集合）不同，整数规划的可行域是离散的

如上图，一条蓝线代表一个线性不等式，但是这里x,y自变量被约束成整数变量，因此可行域变成了红线区域内的9个离散的黑点。（线性规划的可行域是蓝色线段内部所有的区域）

凸包（Convex Hull）：整数规划所有可行解的凸包围，即图中红线组成的多面体（想象多维的情况）。
凸包是未知的，已知的是蓝线的不等式，并且凸包是非常难求解的，或者形成凸包需要指数数量级的线性不等式（图中红线）。
如果知道了凸包的所有线性表示，那么整数规划问题就可以等价为求解一个凸包表示的线性规划问题。

另外，除了整数规划，还有混合整数规划（Mixed Integer Programming, MIP），即自变量既包含整数也有连续变量。如下图：

这里是简单的二维情况，自变量x是连续的，y被约束成整数变量（0,1,..,n）
这时候可行域变成了4条离散的橘黄色线段加上4处的黄色整数点（0,4）

整数规划由于可行域是极度非凸（Highly Nonconvex）的
因此也可以看作是一类特殊的非凸优化（Nonconvex Optimization）问题

算法复杂度

一般情况下，求解整数规划的精确解（全局最优）是NP难的
简单地说，也就是只存在指数级算法复杂度（Exponential Time Solvable）

怎么来理解指数级复杂度呢？
假设这里的整数变量是{0,1}变量，那么我们可以简单地理解为算法复杂度至少是O(2^n)（需要解2^n个线性规划问题，其中n是整数变量的个数）。
其中线性规划被认为是可以较为高效求解的，其复杂度是多项式时间的（O(n^k)，其中k是常数，注意这里n在底数上）。

也就是说，每增加一个整数变量，求解其精确解的运算速度最坏情况下就要增加一倍！
例如求解n=100的整数规划问题需要1小时，那么求解n=101的规模可能会需要2小时，n=102需要4小时，n=105需要32小时，这就是指数爆炸！

因此，整数规划问题被看作数学规划里、乃至世界上最难的问题之一
被很多其他领域（例如机器学习）认为是不可追踪（Intractable）的问题，也就是他们直接放弃治疗了，从不考虑直接求解该问题的精确解，而是退而求其次求解近似解或局部最优解。

精确算法 | 分支定界法

（Branch and Bound Algorithm, B&B）
整数规划的精确算法框架中最核心的便是B&B，以及增加分支定界效率的各种技巧，例如割平面方法（Cutting Planes Method）等。
假设是求解目标函数最小化的问题，它的核心思想便是把这个NP难的问题分解成求解一个个的线性规划（LP）问题（每个LP问题是多项式时间可解），并且在求解的过程中实时追踪原问题的上界（最优可行解）和下界（最优线性松弛解）。
我们先看个简单的例子以便理解。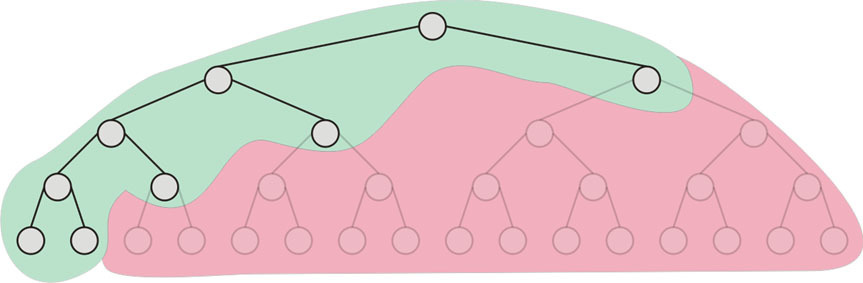


这里假设有4个{0,1}变量，x1..x4，以及1个连续变量x5。
图中最顶上的点叫Root Node，通过把整数变量x1..x4线性松弛(Linear Relaxation)
例如这里松弛成[0,1]区间内的连续变量，然后求解相应的松弛后的线性规划问题(Linear Relaxation Problem)。
求解该LRP问题所得的解（通常对于原问题来说是不可行的，因为x1..x4可能是小数），这个解便是该问题的第一个下界（Lower Bound）。

为什么是下界呢？对于一个最小化问题，因为通过把{0,1}变量松弛成[0,1]，等于增加了可行解的个数（可行域的范围），这样该最小化问题就有可能得到比原问题更好（小）的解，因此松弛后的问题求得的解是原问题的下界（Lower Bound）。

事实上，图中每一个点，都是一个松弛后的线性规划（LRP）问题的解。由于被松弛成了[0,1]间的连续变量
因此原问题中应属于{0,1}的自变量，例如x1，通过求解线性规划，得到的解可能是0.4，显然不满足原问题的条件
这时候，我们就需要做分支（Branch）
例如对Root Node做左右俩个分支，左边的分支可以是x1=0，右边的分支是x1=1
分支的意思，可以理解为在原本Root Node的LRP基础上，加上一个x=0或1的约束条件。
这样，通过加上这个约束条件，再解该问题，x1就必定等于0或1，x1也便是可行的。
当然剩余的自变量x2..x4，由于没有类似的整数约束，还有可能是小数，因此我们还需要更多的分支。
上图4个{0,1}变量，最坏的情况需要2^4次分支，也就是求解16个线性规划问题。

那么图中红色的部分是什么意思呢？

这就需要先引进上界（Upper Bound、最优可行解）的概念。
当分支一个个进行下去时，到某一个Node，松弛后线性规划问题求得的解可能是原问题的可行解，也就是说，x1..x4都是{0,1}。这个时候，我们便找到了一个原问题的可行解，它的目标函数例如4，我们把它放入Upper Bound里。

在接下来的分支里，如果求解一个Node的LRP的解是大于上界4的，例如4.5。
那么这个时候，虽然我们还没找到这个点其下分支可能的可行解，但是如果继续对这个点进行分支，由于分支代表增加更多的约束，减少了可行解的个数，以后求得的解只会比4.5来得更差（大）。
因此，从优化的角度，我们不可能从这个点以后的分支中找到比目前上界4更优的解，因此没有必要对4.5这个点继续再做分支，可以直接删（Prune）掉，也就是图中红色的区域。

这就是分支定界里定界的重要性，它使得你不需要求解所有2^n个LRP问题
因为很多Node及其下面的分支，都被Prune了。

• Prune情况一：下界大于上界
• Prune情况二：该Node的LRP问题无解（Infeasible）。

红色部分表示这部分分支已经被丢弃掉了，因为找到的upper bound（当前最优解）的值小于lower bound（线性规划松弛解），也就是说，即使红色的部分探索下去，找到一个可行解，也不可能比当前找到的最优解要来得好（那么为何还要浪费时间再去探索他们呢？）。

分支定界法的“收敛（Convergence）”

这里的收敛不是分析意义上的收敛，而是算法、计算意义上的。
上面我们提到分支定界法存在上界和下界，并且随着一个个Node LRP问题的求解，不断进行着更新。
每当求得一个原问题的可行解（混合整数解），如果这个解的目标函数小于当前的最优可行解，那么就对上界进行更新。下界更新方式类似。

分支定界法是一个迭代算法(Iteration Algorithm)，每次迭代都在求解LRP问题，收敛的准则是计算意义上的
例如可以设置当上界和下界非常接近（0.001）时，结束迭代

然而比起绝对差值更为流行的，是相对差值，也即分支定界法的Gap。它的计算方法，（上界-下界）/上界。

通常我们设置Gap < 0.1%，就可把当前的最优可行解（上界）理解为该问题的全局最优解了，分支定界法随即终止（Terminate）

启发式/近似算法

（Heuristic/Approximation Algorithms）
作为研究世界上最难问题的学者，想出了解决整数规划问题的各种其他途径
例如：
近似算法（Approximation Algorithms）
启发式算法（Heuristic Algorithms）
遗传算法（Generic Algorithm）
Evolutionary Algorithms等等

它们虽然不能求得整数规划的最优解，但是却能在短时间（通常多项式时间）内给出一个较好的可行解。

启发式算法，通常采用贪心算法（Greedy Algorithm）
所得的解通常只是局部最优解，并且完全没有概念这个解到底有多“好”

近似算法，与启发式算法不一样，算法往往通过非常巧妙的设计，计算所得的解可以用严格的数学证明是“比较好”的，即所谓的近似率（Approximation Ratio）,R。
也就是说，近似算法所得的解，可以被证明是全局最优解的R倍之内。这样该算法所得的解被认为是有保证的。

优化求解器

（Optimization Solver）
分支定界法虽然思想简单，但是实现起来却比想象的复杂
如何管理各个分支的存储，分支的先后顺序，以及一些提高分支定界法效率的算法，等等。

市面上知名的混合整数规划求解器：IBM Cplex，Gurobi，FICO Xpress，SCIP。

前三个都是商业软件，闭源，第四个是开源的由柏林ZIB研究机构开发并维护的，但是商业用途需要购买版权。
这四个如果用作教学、科研，都是免费下载和使用的。

作为运筹学的引擎，优化求解器意义重大，因为所有混合整数规划模型的求解，都需要靠它。
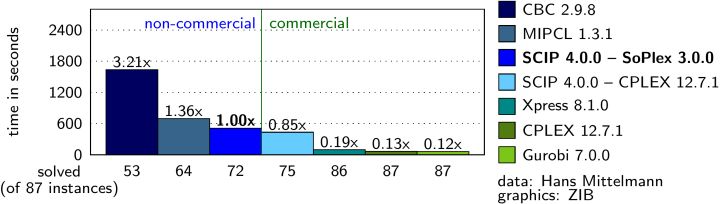
由于是NP难问题，求解的效率至关重要，不同求解器的求解速度也千差万别。
例如同一个问题，用Cplex求解只需1分钟，用SCIP可能就需要1小时，你自己写B&B算法的程序，可能需要1天！（各求解器效率对比）

而工业界非常多的问题可以被建模成整数规划问题，例如物流、路径规划、航班调度等等。
需要得到其精确解，便需要使用优化求解器

整数规划模型意义

既然整数规划模型是NP难的，既然已经有了高效的启发式算法、近似算法，那么为何还要执念于精确算法呢？

一是，数学家的执念，数学家不care具体算法，更关心数学模型。
其二，同一个问题，虽然可以用启发式算法或近似算法，但是求得的解要么完全没有保证，要么只有R这个近似倍数的保证。但是，只要把该问题数学建模成整数规划模型，启发式或近似算法求得的解，都可以直接作为优化求解器的初始解（上界）。这时候，优化求解器只需求解Root Node（LRP），便可以得到下界，于是你几乎不费力（多项式时间）便可得到一个Gap。这个Gap，便可以作为这个解的某种保证（例如，Gap是10%，你便知道这个解离最优解“不远了”）