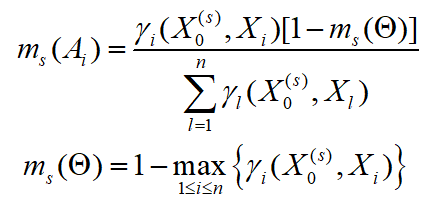- 目标识别是一个比目标跟踪更广泛的概念,包含大量的变量。
- 目标各要素可以采用多种表示技术,每一种表示技术又可以采用不同的方法进行计算
- 因而,在这一领域已开发了许多技术
- 在目前的所有方法中,Bayes与D-S证据理论方法在研究和使用方面最有活力,引起了人们的特别注意
-
1.1 基于 D-S 证据理论的身份识别
Dempster 和 Shafer 在 70 年代提出的证据理论是对概率论的扩展。
- 他建立了命题和集合之间的一一对应,以把命题的不确定性问题转化为集合的不确定性问题,而证据理论处理的正是集合的不确定性。
- Dempster 和 Shafer 在证据理论中引入了信任函数。
- 它满足比概率论弱的公理,并能够区分不确定和不知道的差异。
- 当概率值已知时,证据理论就变成了概率论。
- 因此,概率论是证据理论的一个特例。
- 当先验概率很难获得时,证据理论就比概率论合适。
Blackman 对 Dempster-Shafer 证据理论在身份识别中的应用进行了深入的讨论。
1.1.1 基本理论
设U表示X所有可能取值的论域集合,且所有在U内的元素间是互不相容的,则称U为X的识别框架。
- X可能取值为轰炸机、民航机、歼击机、预警机,U={轰炸机、民航机、歼击机、预警机}。
- U为X的识别框架。
- 定义:设U为一识别框架,则函数
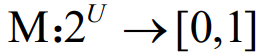 ,且满足
,且满足
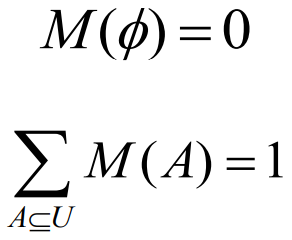
则称M是
上的概率分配函数,M(A)称为A的基本概率赋值,M(A)表示对命题A的精确信任程度,表示了对A的直接支持(精确信任)
定义:设 U 为一识别框架,则函数
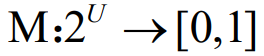 是 U 上的基本概率赋值,定义函数
是 U 上的基本概率赋值,定义函数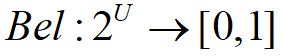 ,且
,且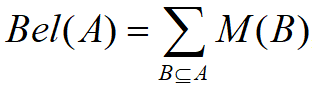 对所有的
对所有的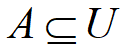 称该函数是 U 上的信任函数。
称该函数是 U 上的信任函数。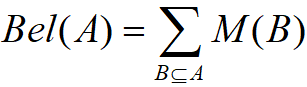 表示 A 的所有子集的可能性度量之和(对A的子集的信任也是对A的信任),即表示对A的总信任。由概率分配函数的定义容易得到:
表示 A 的所有子集的可能性度量之和(对A的子集的信任也是对A的信任),即表示对A的总信任。由概率分配函数的定义容易得到:
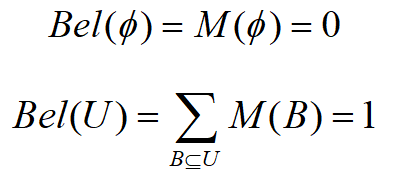
- 定义:设 U 为一识别框架,则定义函数
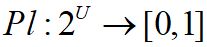 ,且
,且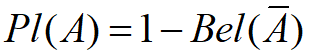 ,对所有的 , 也称为似真度函数,表示对A非假的信任程度。容易证明信任函数和似然函数有如下关系:
,对所有的 , 也称为似真度函数,表示对A非假的信任程度。容易证明信任函数和似然函数有如下关系:
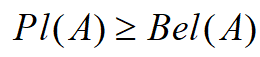
- 对所有的
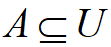 ,A的不确定性由
,A的不确定性由 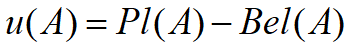
- 表示
- 对偶
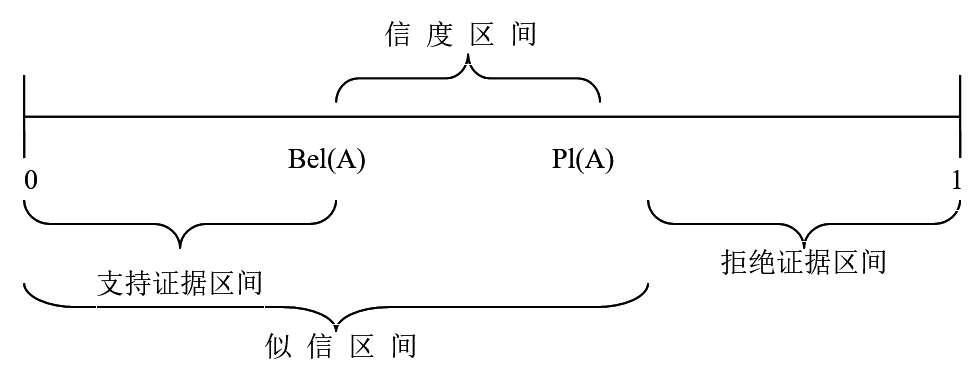
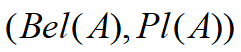 称为信任区间,它反映了关于 A 的许多重要信息。Dempster-Shafer证据理论对 A 的不确定性的描述可以用图表示
称为信任区间,它反映了关于 A 的许多重要信息。Dempster-Shafer证据理论对 A 的不确定性的描述可以用图表示 - 例如:
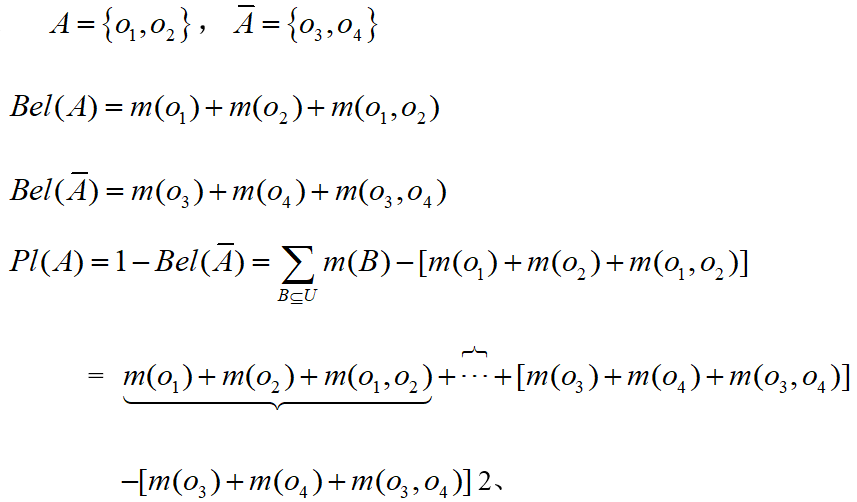
- 中间省略了不确定部分,故称为A的不确定性。
定义:若识别框架 U 的一子集为 A ,具有 M(A)>0,则称 A 为信任函数
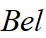 的焦元,所有焦元的并称为核
的焦元,所有焦元的并称为核
1.1.2 证据理论的组合规则
证据理论的组合规则提供了组合两个证据的规则。设
和
是 U 上的两个相互独立的基本概率赋值,现在问题是如何确定组合后的基本概率赋值:
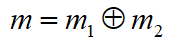
- 定义:若一识别框架 U,
和
分别是该识别框架上两个的基本概率分配函数,焦元分别是
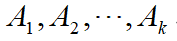 和
和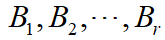 ,又设
,又设
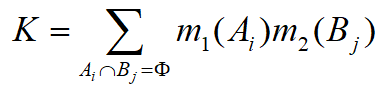
- 则组合规则为
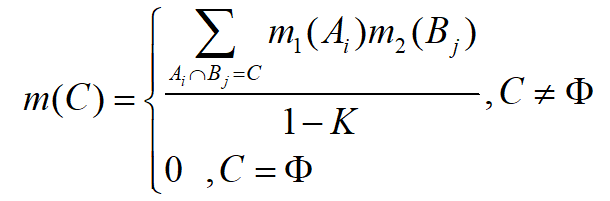
若 K 不等于 1,则 m 确定一个基本概率赋值;若 K 等于1,则认为两条证据相互矛盾,不能进行组合
1.1.3 D-S证据理论的身份识别中应用例子
现考虑一个多传感器数据融合的例子。设
表示民航机,
表示歼击机,
表示轰炸机,
表示预警机,
表示其他飞行器,目标识别框架
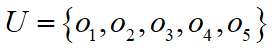 ,系统使用ESM,IR,EO三种传感器。
,系统使用ESM,IR,EO三种传感器。- 三种传感器:
- ESM:电子侦察机,无源传感器。它主要通过发射体的发射频率和脉宽,对目标进行识别,能够截获发射体频率
- IR:红外搜索传感器,接收回波。主要利用多个波段同时测量目标的多频谱特征,根据目标频谱特征对目标进行分类
- EO:光电传感器。通过测量可视频谱的对比度,把目标从背景中区分出来。
- 由射频RF、脉宽PW、波长IR及光学设备确定的基本概率赋值如下表1所示,其中
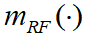 和
和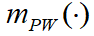 由 ESM 传感器确定。首先按证据理论的组合公式对
由 ESM 传感器确定。首先按证据理论的组合公式对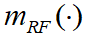 和
和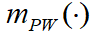 组合得到ESM传感器关于目标识别的基本概率赋值,组合情况如表2所示
组合得到ESM传感器关于目标识别的基本概率赋值,组合情况如表2所示
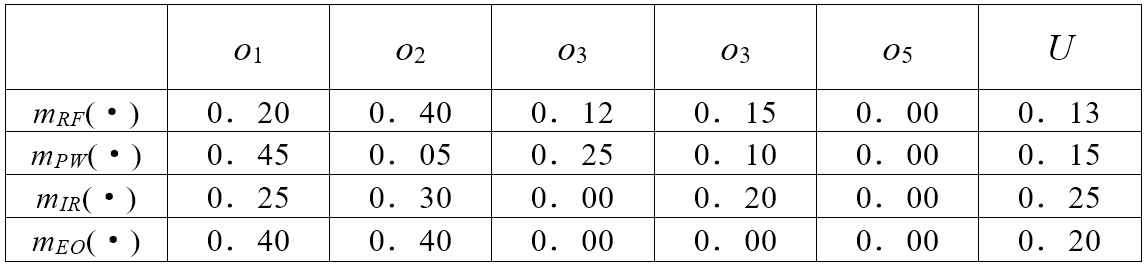
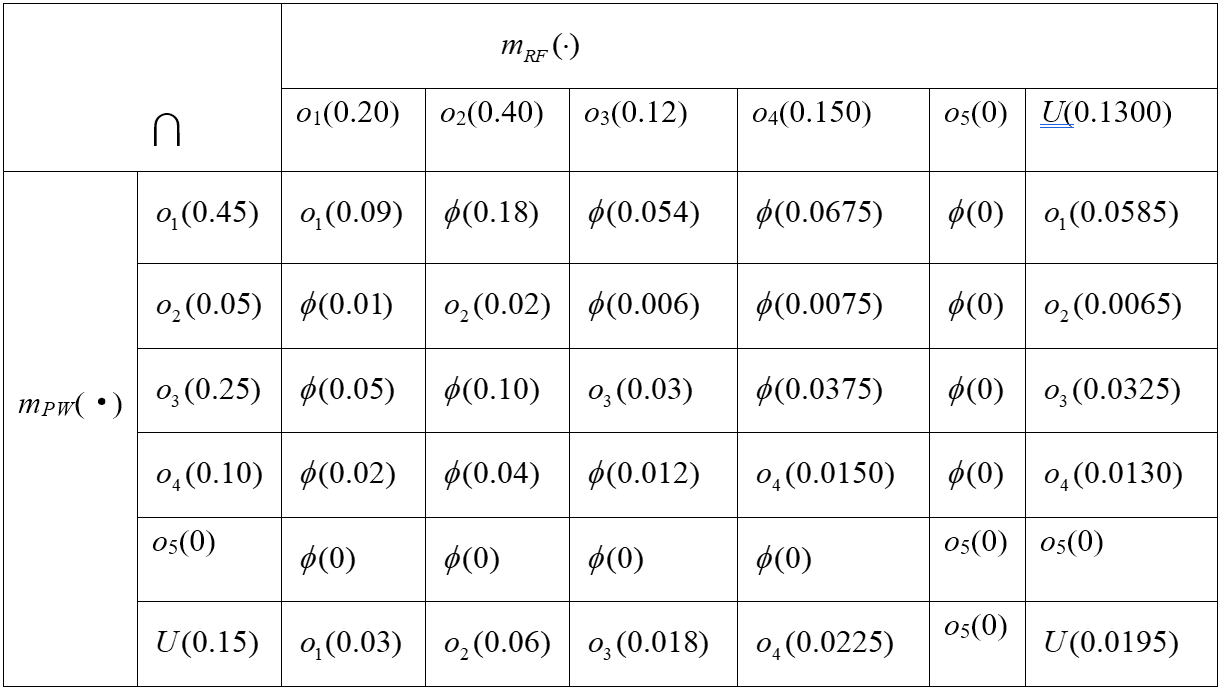
- 其中 Φ 表示空集,由表2可得
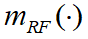 和
和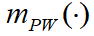 这两批证据的不一致因子K:
这两批证据的不一致因子K: - K=0.18+0.054+0.0675+0.01+0.006+0.0075+0.05+0.1+0.0375+0.02+0.04+0.012=0.5845
- 于是,可得ESM传感器目标识别的基本概率赋值为
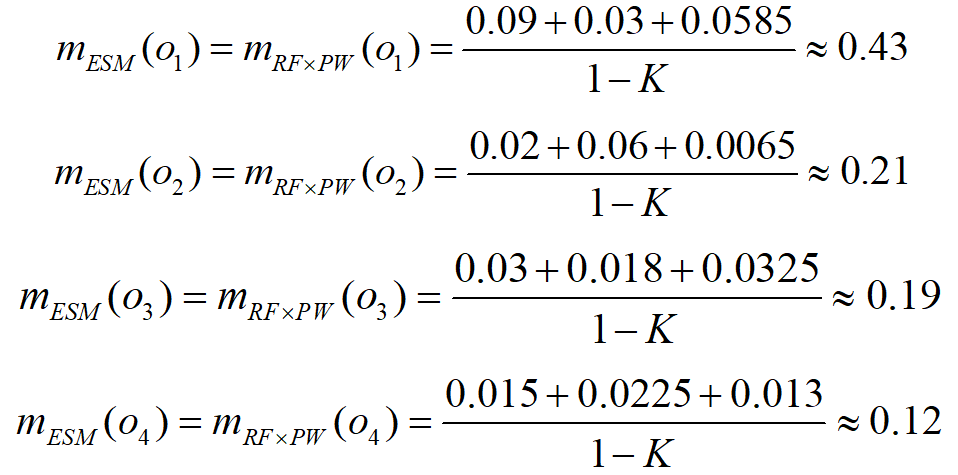
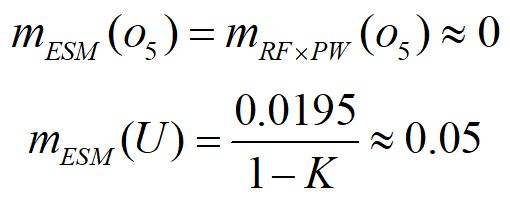
- 同理,将ESM和IR证据融合后的基本概率赋值为
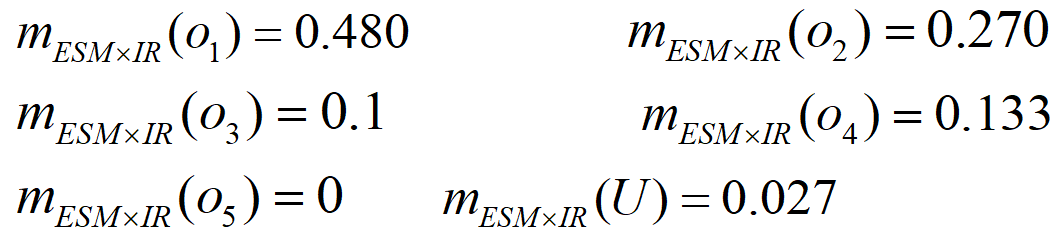
- 把ESM,IR,EO三种传感器融合后的基本概率赋值为
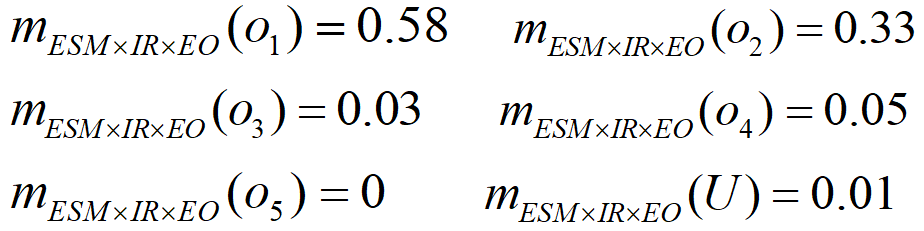
- 将上述融合结果总结为表3中,由计算结果可以看出,通过融合,不确定性的基本概率赋值下降0.01。当采用基于基本概率赋值的决策方法时,若选择门限==0.1,则最终的决策结果是
,即目标是民航机
1.1.4 BPA(Basic Probability Assignment Function)生成
- 在D-S 证据理论中,没有给出基本概率分配函数的一般形式,一般根据经验由主观给出,是某种可信度。
- 在基于DS证据理论的目标识别融合中,基本概率赋值的获取与实际应用密切相关。
下面给出一种用经验获取基本概率赋值的方法。
根据灰色关联度获得基本概率赋值:
- 根据灰色关联度获得基本概率赋值函数的步骤如下:
- 假定识别框架为
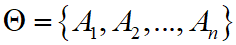 ,共有 n 个目标类型。每个目标类型有 k 个特征参数,它们组成了一个 k 维特征向量。
,共有 n 个目标类型。每个目标类型有 k 个特征参数,它们组成了一个 k 维特征向量。 - 选定参考数据序列,定义为
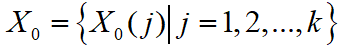 。比较数列定义为
。比较数列定义为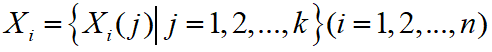
- 为了保证数据具有可比性,在进行灰色关联分析时,需要对数据进行无量纲处理,目的是为了消除数量级大小不同的影响,以便于进行计算和比较分析。
- 首先对比较数据进行无量纲处理如下:
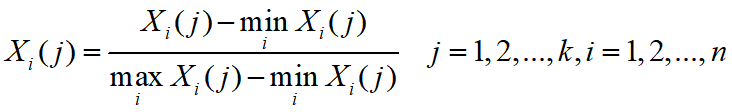
- 对无量纲化的数据取参考序列
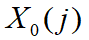 和比较序列
和比较序列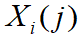 ,计算其关联系数为:
,计算其关联系数为:
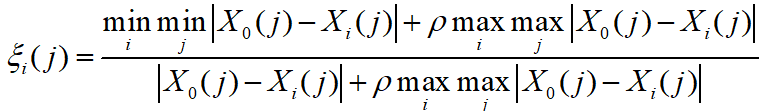
- 令
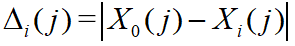 ,则得到:
,则得到:
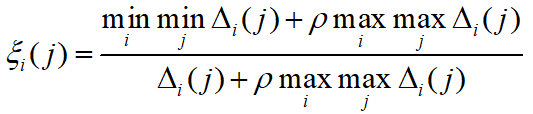
- 其中,ρ 为分辨系数,通常取 ρ 为0.5。
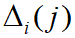 为差序列,
为差序列, 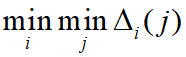 为两级最小差,
为两级最小差, 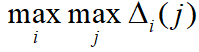 为两级最大差。
为两级最大差。 - 下面讨论 ρ 的取值范围对关联系数的影响:
- 当
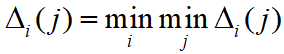 时,
时, 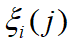 达到最大为 1。当
达到最大为 1。当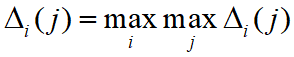 时,
时, 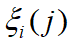 达到最小,为
达到最小,为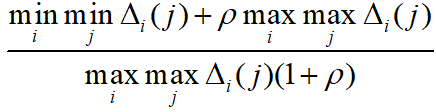 ,该值大于等于
,该值大于等于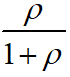 。即
。即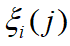 的范围为
的范围为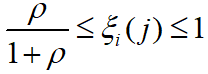 。如令
。如令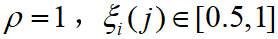 ;令
;令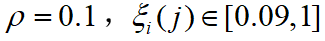 。可以看出, ρ 越小,分辨力越大。
。可以看出, ρ 越小,分辨力越大。 - 从而可得
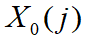 与
与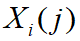 的相关系数为
的相关系数为
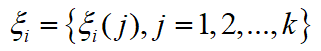
- 为了体现数据序列的相关程度,引入灰关联度 。考虑目标类型各个特征参数的重要程度,加权灰关联度定义为:
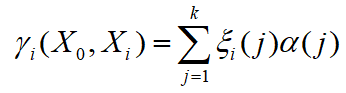
- 其中,
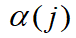 为加权系数,
为加权系数,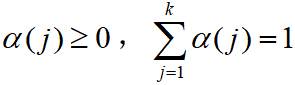 。
。 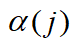 由具体环境而定,常用的计算方法是取多个关联系数的均值,即
由具体环境而定,常用的计算方法是取多个关联系数的均值,即 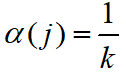
- 同时,引入灰关联度集合:
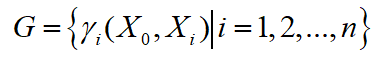 。
。 - 假定对同一目标进行 t 次采样,即
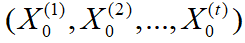 。同理可得灰关联度集
。同理可得灰关联度集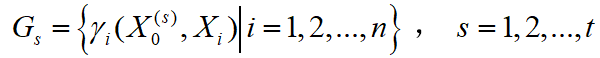 。这样,相关的基本因素集为
。这样,相关的基本因素集为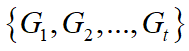 。
。 - 从而,基本概率赋值函数
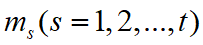 可以写成:
可以写成:
1.1.5 开放世界封闭世界假设
- 在证据理论的应用中,通常需要首先确定一个包含所有可能命题的完备的识别框架。
- 但对于一些具体问题,尤其是实时应用中,新证据随着时间的推移而不断出现,此时往往无法预先准确确定一个完备的封闭识别框架,而只知道识别框架中的一部分可能命题,甚至是一无所知。
- 如何处理这种识别框架的不完备性,是证据理论中一个比较突出的问题。
- 当前处理这种不完备识别框架的代表性方法是Smets提出的“开放世界假设(Open world assumption)”。
- 在开放世界假设中,Smets把对空集 的基本概率赋值 定义为“真命题在当前己知识别框架之外”的信任度,证据组合中取消对组合结果的归一化,而把两个证据组合产生的冲突归于 。
- 但是,开放世界假设方法实际上并没有在理论上和应用上根本解决识别框架不完备问题。
- 首先,开放世界假设把组合过程中的“证据冲突”等价于“识别框架不完备”,这种方法缺乏理论依据,也不符合一般常识,因为证据冲突并不一定是由识别框架的不完备造成的。
- 其次,“开放世界假设”认为一个识别框架可能并没有包括所有可能的命题,这就意味着不同的证据可能会有不同的识别框架,显然与识别框架本身的概念有相背之处。
并且,如果一个新证据包含原识别框架中所没有的命题,该证据应该如何与现有证据进行组合,在开放世界假设下 并没有一个明确可行的方法。
1.1.6 证据冲突例子
在实际应用中,当利用组合规则来组合来自多个信息源的证据时(如多传感器、专家意见、多分类器等),这些证据之间的信息不可能完全一致,往往相互之间存在着冲突。下面给出一个证据冲突的例子:
- 设识别框架
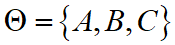 ,现有两条证据如下:
,现有两条证据如下:
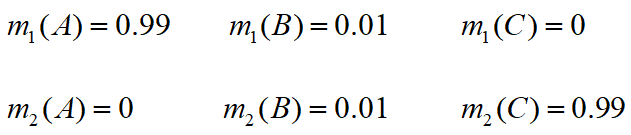
- 对两条证据进行合成,首先计算证据的冲突程度 K :
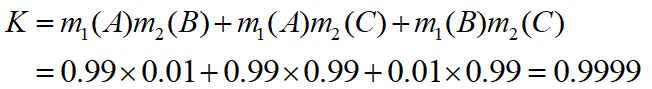
- 由于
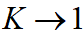 , K 接近1,表示证据冲突程度很大,此时若用Dempster-Shafer合成法则合成,其结果为:
, K 接近1,表示证据冲突程度很大,此时若用Dempster-Shafer合成法则合成,其结果为:
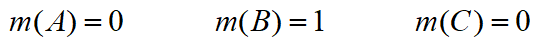
- 由此可见,两条证据对 B 的支持程度为0.01,而融合结果却是1。故当证据冲突接近 1 时,D-S 合成公式的结论有悖于常理。