数学规划模型
线性规划(LP)
(Linear Programming)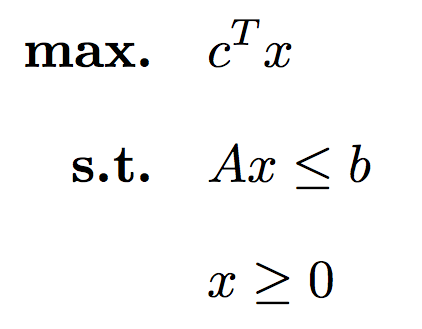
最简单和基础的优化问题,如上图,目标函数(max)和约束条件(s.t.)都是线性的,自变量x是实数变量,P问题(多项式时间可解)
整数线性规划(ILP)
混合整数线性规划(MILP)
(Mixed Integer Programming)
自变量有整数变量,NP难问题(指数级算法复杂度)
动态规划(Dynamic Programming)、近似算法(Approximation Algorithms)、启发式算法(Heuristic Algorithms, Meta Heuristics)、遗传算法 (Genetic Algorithms)—用来解例如整数规划等NP难优化问题的算法,后俩个通常只能得到局部最优解,最经典的当属最大流最小割定理衍生出来的一些最大流算法(全局最优)被广泛得用在各个学科和领域,如人工智能
非线性规划(NLP)
(Nonlinear Programming)
目标函数或约束条件为非线性,例如2次函数
二次规划(QP)
多目标规划(MOP)
(Muti-objective Optimization)
优化的目标函数是一个向量,通常通过引入权重权衡个目标函数,转化成单目标优化
或者寻找帕累托最优(Pareto Optimality)
动态规划(DP)
(Dynamic Programming)
用来解例如整数规划等NP难优化问题的算法
凸优化(CO)
(Convex Optimization)
约束条件形成的可行域(feasible region)是凸的
半正定规划
(Semi-definite Programming)
每一个自变量x代表一个矩阵
鲁棒优化
(Robust Optimization)
目标函数或约束条件有扰动(不确定性)的情况下,求解其最坏情况下的最优解
双层优化
(Bilevel Optimization)
和复合函数的概念类似,比如Max-Min Problem,在一个优化问题外嵌套另一个优化问题,通常用迭代法
随机优化
(Stochastic Programming)
加入了不确定的因素(通常以概率形式表现,目标函数变成求期望最大化)
最优控制
(Optimal Control)
严格说属于控制论的范畴,可以简单地把它理解为,优化问题中的变量由x变为f(x),并且通常f是时间t的函数(或者状态state的函数),约束条件常有偏微分方程。
也就是说,控制论期望通过解一个优化问题,得到一个最优的函数f(t),使得这个函数在全局(空间+时间)上是最优的。而运筹学通过解一个优化问题,得到的是最优解x,使得目标函数在一个确定性(deterministic,通常与t无关,或者可以理解为在t的某一时刻)的环境下是最优的。
微分方程组模型
阻滞增长模型
SARS传播模型
图论与网络优化问题
最短路径问题
网络最大流问题
网络流问题(Network Flow Problems)
一个特殊的混合整数规划问题,满足一个节点流出流量=流入流(最大流最小割定理)
最小费用最大流问题
最小生成树问题(MST)
旅行商问题(TSP)
图的着色问题
概率模型
决策模型
随机存储模型
随机人口模型
报童问题
Markov链模型
组合优化经典问题
多维背包问题(MKP)
背包问题:个物品,对物品,体积为,背包容量为。如何将尽可能多的物品装入背包。
多维背包问题:个物品,对物品,价值为,体积为,背包容量为。如何选取物品装入背包,是背包中物品的总价值最大。
多维背包问题在实际中的应用有:资源分配、货物装载和存储分配等问题。该问题属于难问题。
二维指派问题(QAP)
工作指派问题:个工作可以由个工人分别完成。工人完成工作的时间为。如何安排使总工作时间最小。
二维指派问题(常以机器布局问题为例):台机器要布置在个地方,机器与之间的物流量为,位置与之间的距离为,如何布置使费用最小。
二维指派问题在实际中的应用有:校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。
旅行商问题(TSP)
旅行商问题:有个城市,城市与之间的距离为,找一条经过个城市的巡回(每个城市经过且只经过一次,最后回到出发点),使得总路程最小。
车辆路径问题(VRP)
车辆路径问题(也称车辆计划):已知个客户的位置坐标和货物需求,在可供使用车辆数量及运载能力条件的约束下,每辆车都从起点出发,完成若干客户点的运送任务后再回到起点,要求以最少的车辆数、最小的车辆总行程完成货物的派送任务。
TSP问题是VRP问题的特例。
车间作业调度问题(JSP)
车间调度问题:存在个工作和台机器,每个工作由一系列操作组成,操作的执行次序遵循严格的串行顺序,在特定的时间每个操作需要一台特定的机器完成,每台机器在同一时刻不能同时完成不同的工作,同一时刻同一工作的各个操作不能并发执行。如何求得从第一个操作开始到最后一个操作结束的最小时间间隔。

