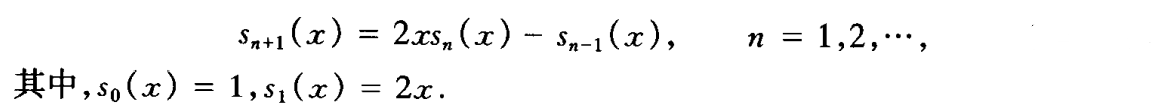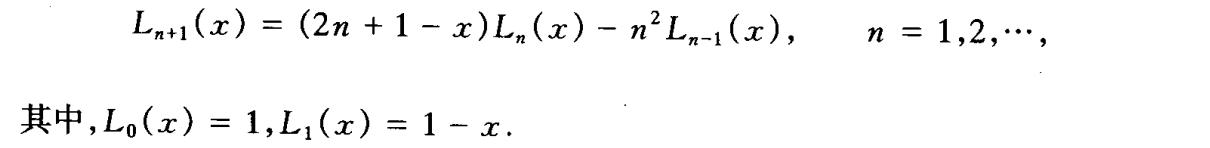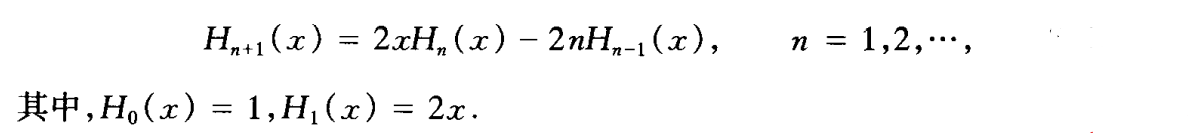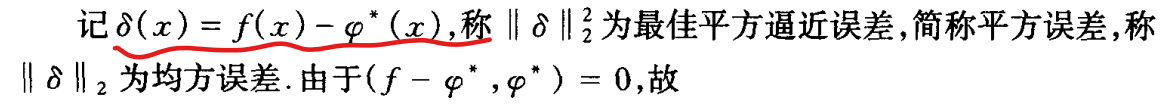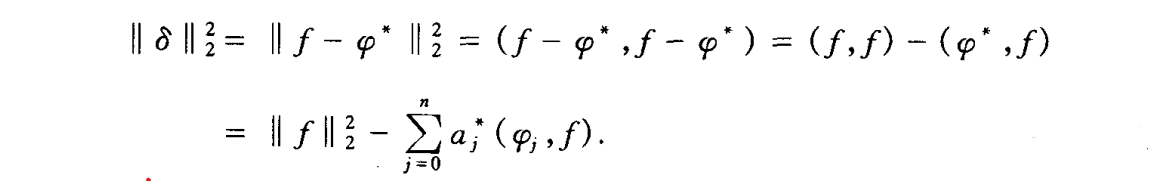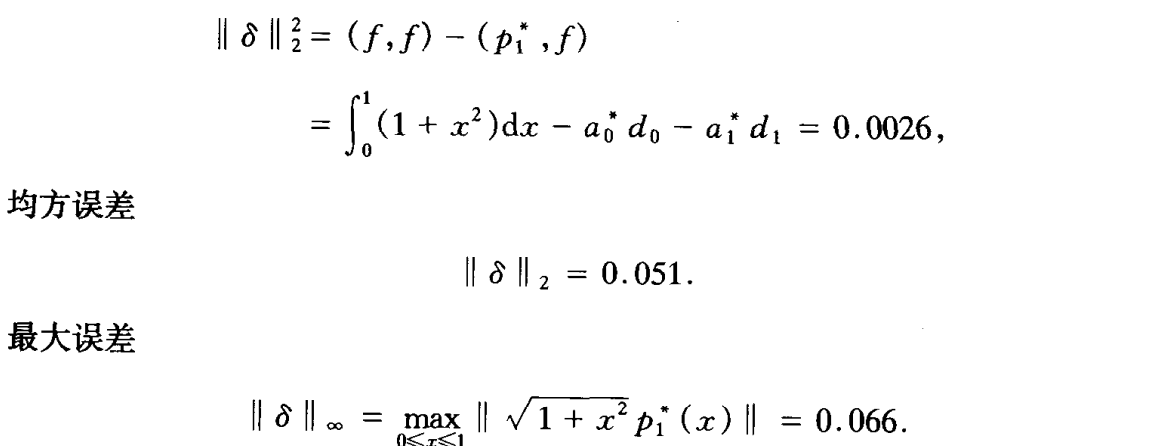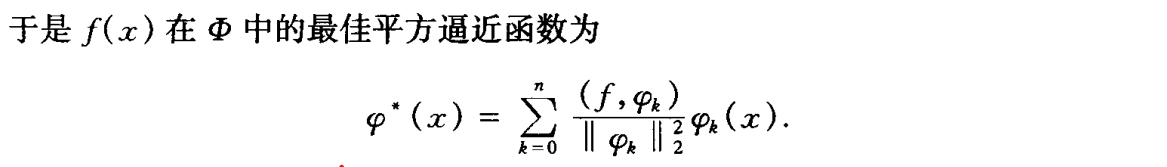正交多项式及其性质

权函数

image.png

函数内积

  • 类比离散函数内积

【数值分析】曲线拟合的最佳平方逼近 - 图2

  • 得到连续函数内积

【数值分析】曲线拟合的最佳平方逼近 - 图3

  • 此时的ρ(x)对应的为范围内每一点的权值
  • 类比向量同样具备性质：

【数值分析】曲线拟合的最佳平方逼近 - 图4

  • 同样，函数内积也存在范数

【数值分析】曲线拟合的最佳平方逼近 - 图5

  • 如果【数值分析】曲线拟合的最佳平方逼近 - 图6就说明f和g很像

    正交性

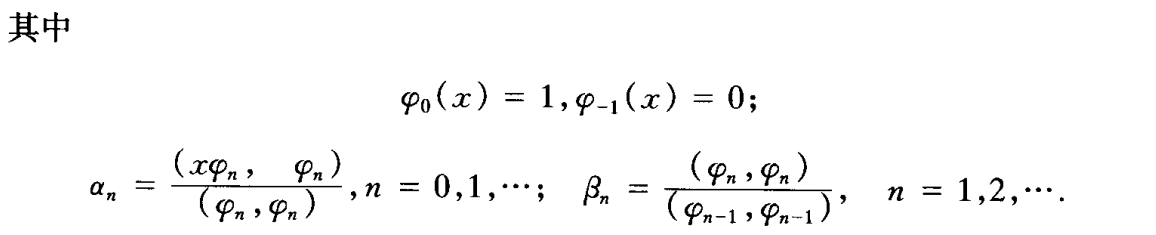
    image.png
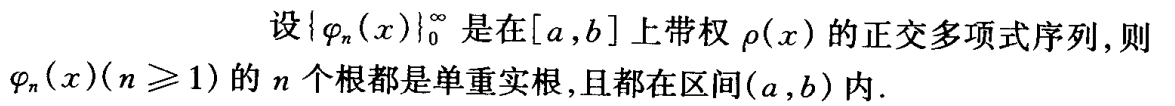
    image.png

  • “首1”多项式序列：

【数值分析】曲线拟合的最佳平方逼近 - 图9

  • 递推公式

image.png
image.png

  • 存在定理

image.png

  • 为满足正交函数族，即他们之间线性无关，存在充分必要条件

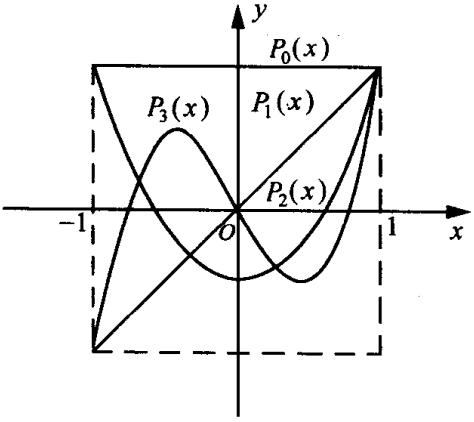
image.png

Legendre多项式

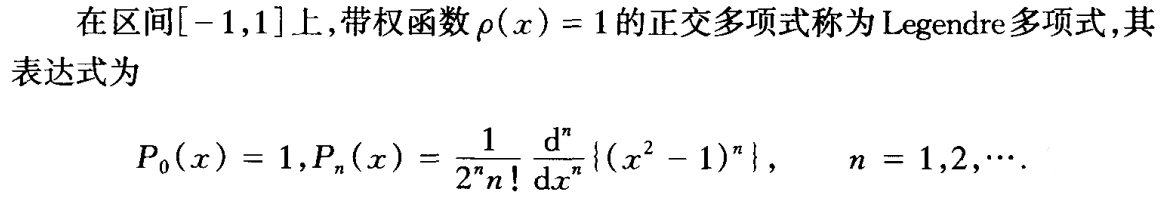
image.png

  • 此处虽然限制了区间[-1,1]，实际上可以映射到任意区间，通过y=kx+b映射到[m,n]。(待定系数)
  • 具备正交性

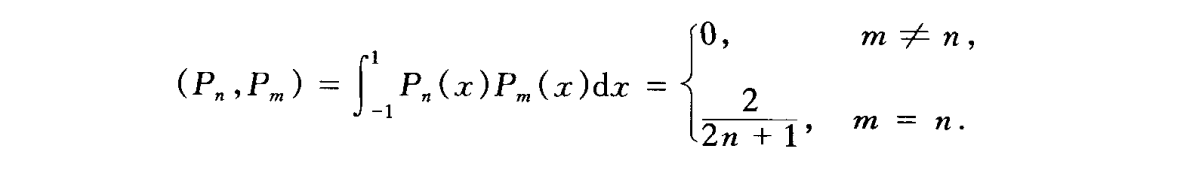
image.png

  • 递推公式

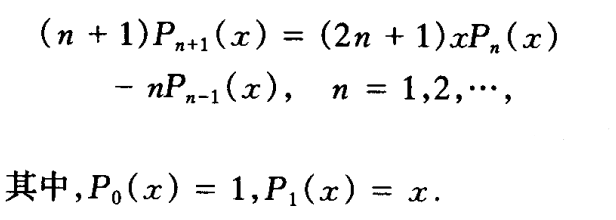
image.png

  • 对称性

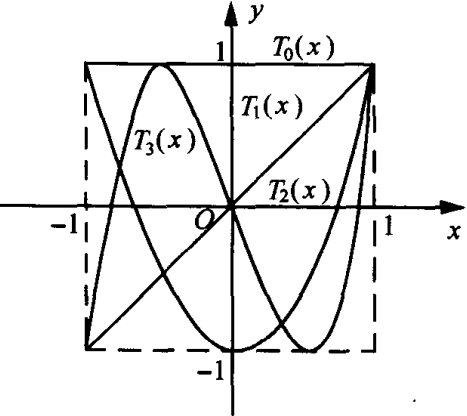
image.png

Chebyshev多项式

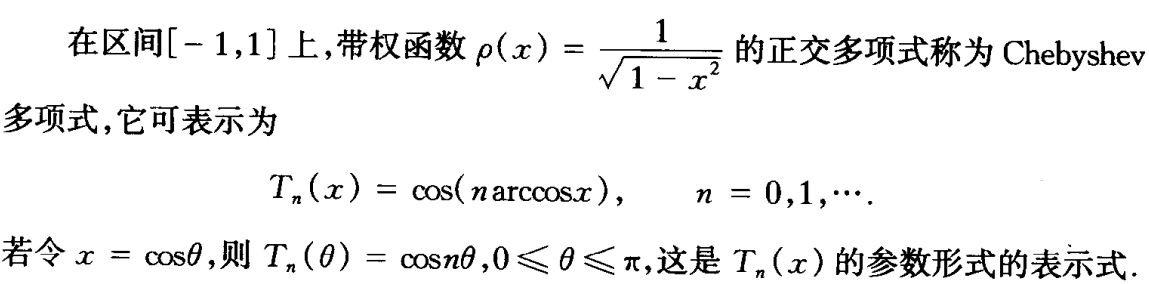
image.png

  • 正交性

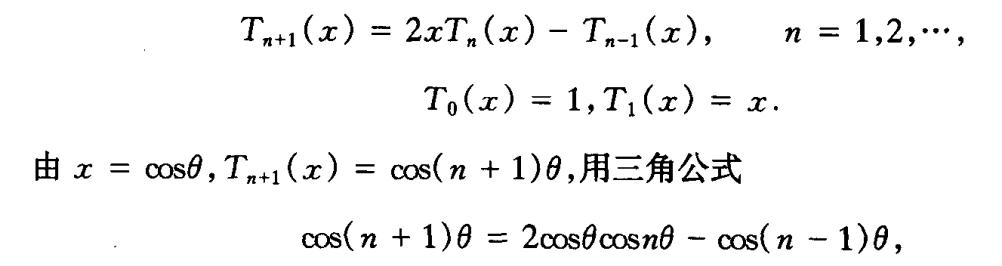
image.png

  • 递推公式

image.png

  • 对称性

image.png

第二类Chebyshev多项式

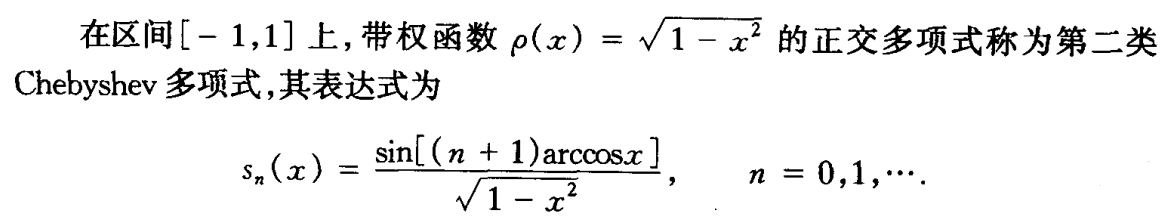
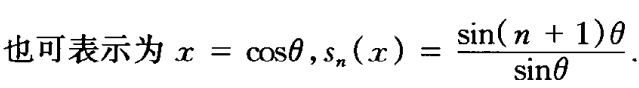
image.png
image.png

  • 正交性

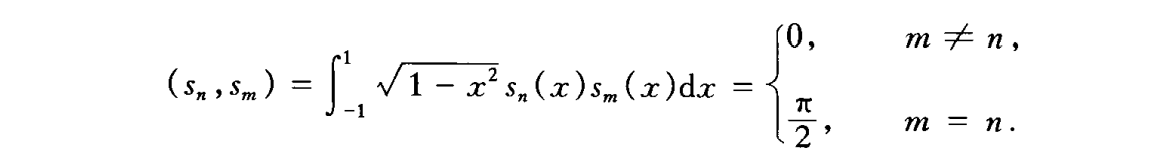
image.png

  • 递推公式

image.png

Laguerre多项式

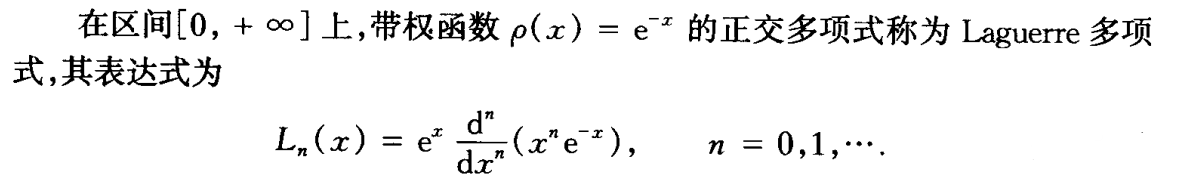
image.png

  • 正交性

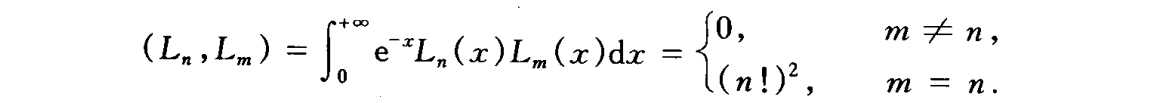
image.png

  • 递推公式

image.png

Hermite多项式

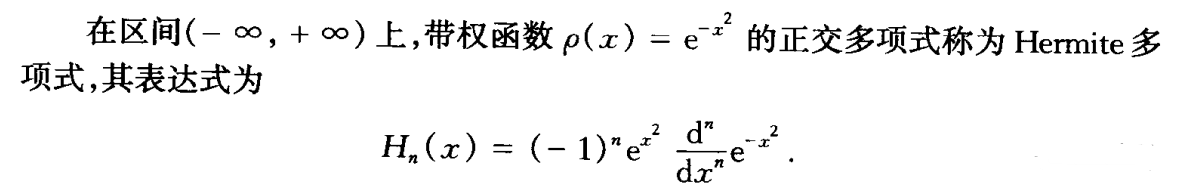
image.png

  • 正交性

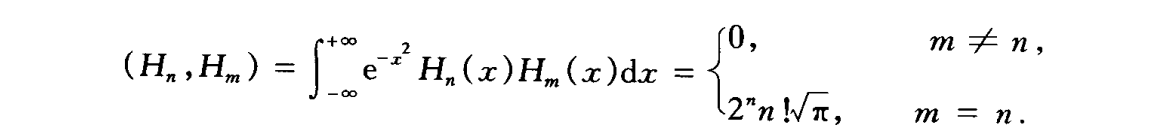
image.png

  • 递推公式

image.png

函数的最佳平方逼近

逼近函数

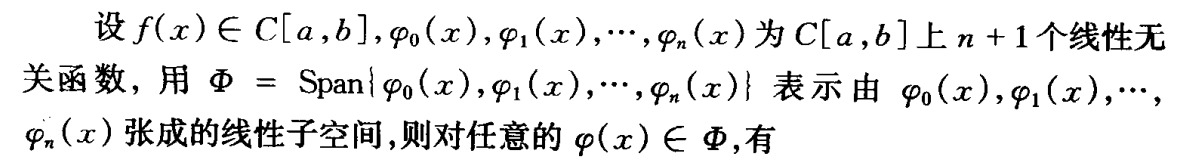
image.png

  • 即从空间中任取一个都可以用基线性表示

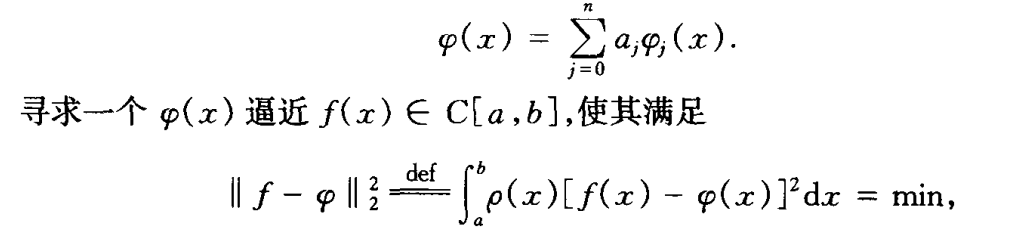
image.png

  • 范数是判断逼近像与不像的标准之一

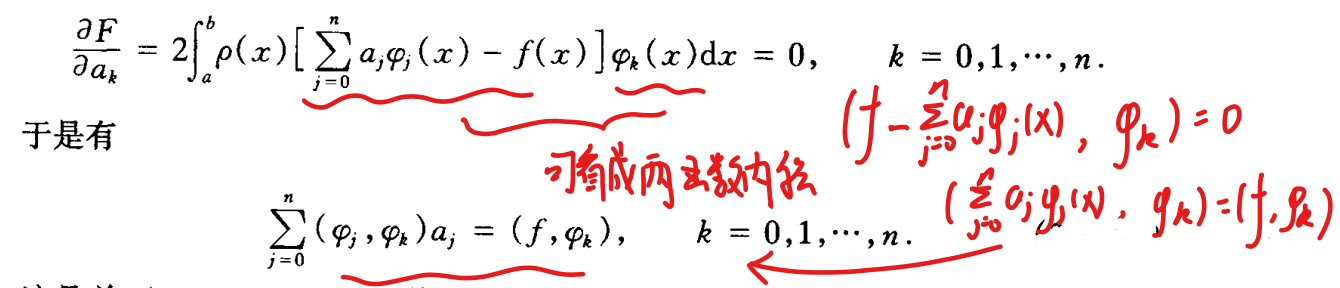
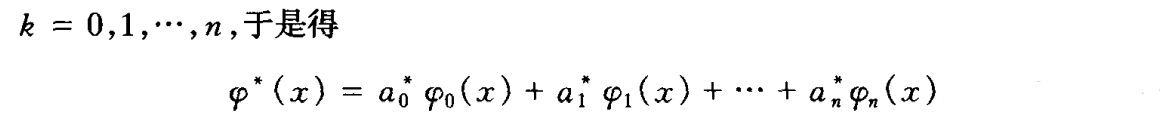
image.png
image.png
image.png
image.png
image.png
image.png
image.png

  • 可以证明，对任意的φ(x)∈Φ有

【数值分析】曲线拟合的最佳平方逼近 - 图41

平方误差

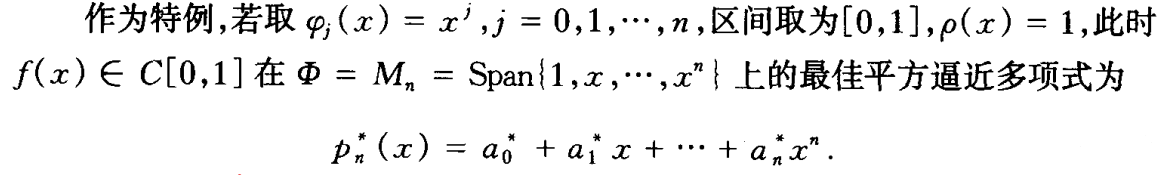
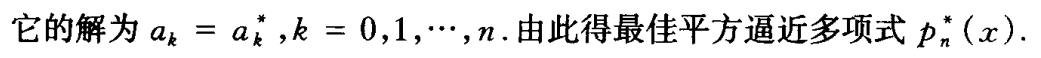
image.png
image.png

举个特例

image.png
image.png
image.png
image.png

  • 存在问题

image.png

  • 例题

image.pngimage.png

正交函数族平方逼近

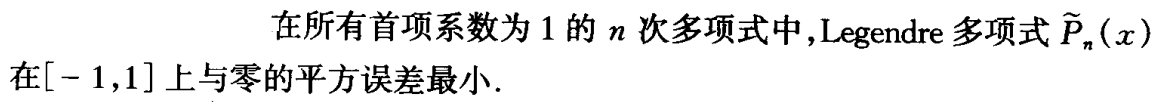
image.png
image.png
image.png

举个特例

image.png

存在定理

image.png

  • 例题

image.pngimage.png