提出问题
传统经典的滤波器都是基于信号已知,或者噪声已知的情况下,通过固定的数学处理得到期望的信号。
较适合于双方约定好固定频率的通信或设计去除固定频率杂波的限波器使用。
在随机性较大的通信或控制领域,传统的数字滤波器较难满足需求。
尤其是当期望滤除掉电路中的热噪声这类型的高斯白噪声(功率谱密度均匀)时,传统滤波器便不再适用。
自适应滤波
- 自适应滤波,就是利用前一时刻以获得的滤波器参数的结果,自动的调节现时刻的滤波器参数,以适应信号和噪声未知的或随时间变化的统计特性,从而实现最优滤波。
- 自适应滤波器实质上就是一种能调节自身传输特性以达到最优的维纳滤波器。
- 自适应滤波器不需要关于输入信号的先验知识,计算量小,特别适用于实时处理。
- 维纳滤波器参数是固定的,适合于平稳随机信号。
- 卡尔曼滤波器参数是时变的,适合于非平稳随机信号。
- 然而,只有在信号和噪声的统计特性先验已知的情况下,这两种滤波技术才能获得最优滤波。
- 在实际应用中,常常无法得到信号和噪声统计特性的先验知识。
- 在这种情况下,自适应滤波技术能够获得极佳的滤波性能,因而具有很好的应用价值。
常用的自适应滤波技术有:
最小均方(LMS)自适应滤波器
递推最小二乘(RLS)滤波器格型滤波器
无限冲激响应(IIR)滤波器
LMS算法原理
基本思想就是对历史输入序列加权求和,得到当前时刻的输出值
而权重是由历史输出和期望输出的偏差计算得来
通过偏差动态修改权重以使偏差趋于0(这也是算法能够实现自适应的体现)
令当前输出值为,
历史输入值为,
为阶数
权重为
期望输出值为
偏差值为
存在关系
写成向量形式
因为LMS算法的目标是找到一组权重,使实际输出与期望输出最接近
需要设置一个代价函数,来衡量权重的选取效果,这个代价函数对权重可微
LMS最小均方算法即体现在代价函数的选取上
为代价函数的瞬时值
对权重求偏导
因此权重的迭代关系为
其中为学习率参数或者叫收敛因子,可以通过调整它来调整输出趋于期望的步长
学习率参数的选取有点像经验数值,但存在一个选取范围
要求大于0,小于xn的相关矩阵最大特征值的倒数
学习率参数不宜设置太大
滤波器结构
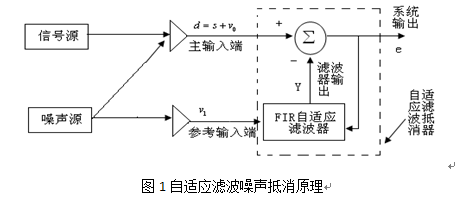
图1给出了用自适应噪声抵消技术来解决噪声背景中的信号提取问题的基本原理。
主输入端接收从信号源发来的信号s但是受到噪声源的干扰收到噪声vo。
参考输入端的参考信号为vi是一个与有用信号s无关但与vo相关的噪声信号。
主输入中含有待抵消的加性噪声,参考输入对准主输入中的噪声vo。
利用两输入噪声的相关性和信号与噪声的独立性,使参考输入通过自适应滤波器与主输入中噪声分量逼近并相减,输出误差信号。
自适应滤波算法决定滤波器对参考信号 v1的处理,使得滤波器的输出尽可能地逼近主输入中的干扰成分。
所以,在最佳准则意义下滤波器的输出v逼近vo等效于系统的输出e逼近s。
从而在噪声对消器的输出端大大地提高了信噪比。
但若参考通道除检测到噪声v1外,还收到信号分量,则自适应滤波器的输出中将包含信号分量,从而使噪声对消效果变坏。
因此,为获得良好的噪声对消性能,应使参考通道检测到的信号尽可能小,在信号不可测的噪声环境拾取参考输入信号。
在实际使用滤波器的过程中,纯噪声信号即为输入信号,有用信号和噪声的叠加信号为期望信号,滤波器输出的应该为期望信号与学习结果产生信号的差值。
编写代码
%----------滤波器-------------------------------------------------global M;global x_Array;global W_Array;M = 10; % 滤波器阶数x_Array = zeros(1,M); % 输入窗口W_Array = zeros(1,M); % 加权参量%Input_2为噪声,Input为混合信号Output = zeros(1,length(Input));for N = 1:length(Input)Output(N) = LMSfilter(Input_2(N),Input(N),0.002);end%-----------------------------------------------------------------
令滤波器的阶数,选取的输入值窗口,动态变化的权重,作为全局变量,便于滤波器函数使用和修改
需要用到输入序列的长度作为循环的次数,即调用滤波器的次数
滤波器输入参数为
- 当前输入值,当前期望值,学习率(收敛因子/步长)
输出参数为
- 当前输出值
历史值在滤波器函数内更新
% 输入参数:% xn 当前输入值% dn 当前期望% mu 收敛因子(步长)% 输出参数:% en 误差序列function en = LMSfilter(xn,dn,mu)global x_Array;global W_Array;global M;%更新选取的x_Array窗口序列x_cul = x_Array(2:M);x_cul(M) = xn;x_Array = x_cul;yn = W_Array * x_cul'; % 学习结果en = dn - yn ; % 误差% 滤波器权值计算的迭代式W_Array = W_Array + mu*en*x_cul;end
热噪声滤波
热噪声在功率谱上的分布为均匀分布,而在频域和时域上的分布杂乱无章,我们在matlab中使用提供的信号源产生一个满足高斯分布的热噪声,同时添加一个频率为1Hz的有用信号,因为热噪声为加性噪声,与有用信号叠加后我们将其通过LMS自适应滤波器后观察
N = 2000;fs = 1000;%(Hz)t = (0:N-1)/fs;Freq = (0:N-1)*fs/N;%有用信号f1 = 1;%HzInput_1 = 3*sin(2*pi*f1*t);%产生一个高斯白噪声信号Input_2 = wgn(1,N,2);Input = Input_1+Input_2;Input_fft = fft(Input);%----------滤波器-------------------------------------------------global M;global x_Array;global W_Array;M = 10; % 滤波器阶数x_Array = zeros(1,M); % 输入窗口W_Array = zeros(1,M); % 加权参量Output = zeros(1,length(Input));for N = 1:length(Input)Output(N) = LMSfilter(Input_2(N),Input(N),0.002);end
- 时域上
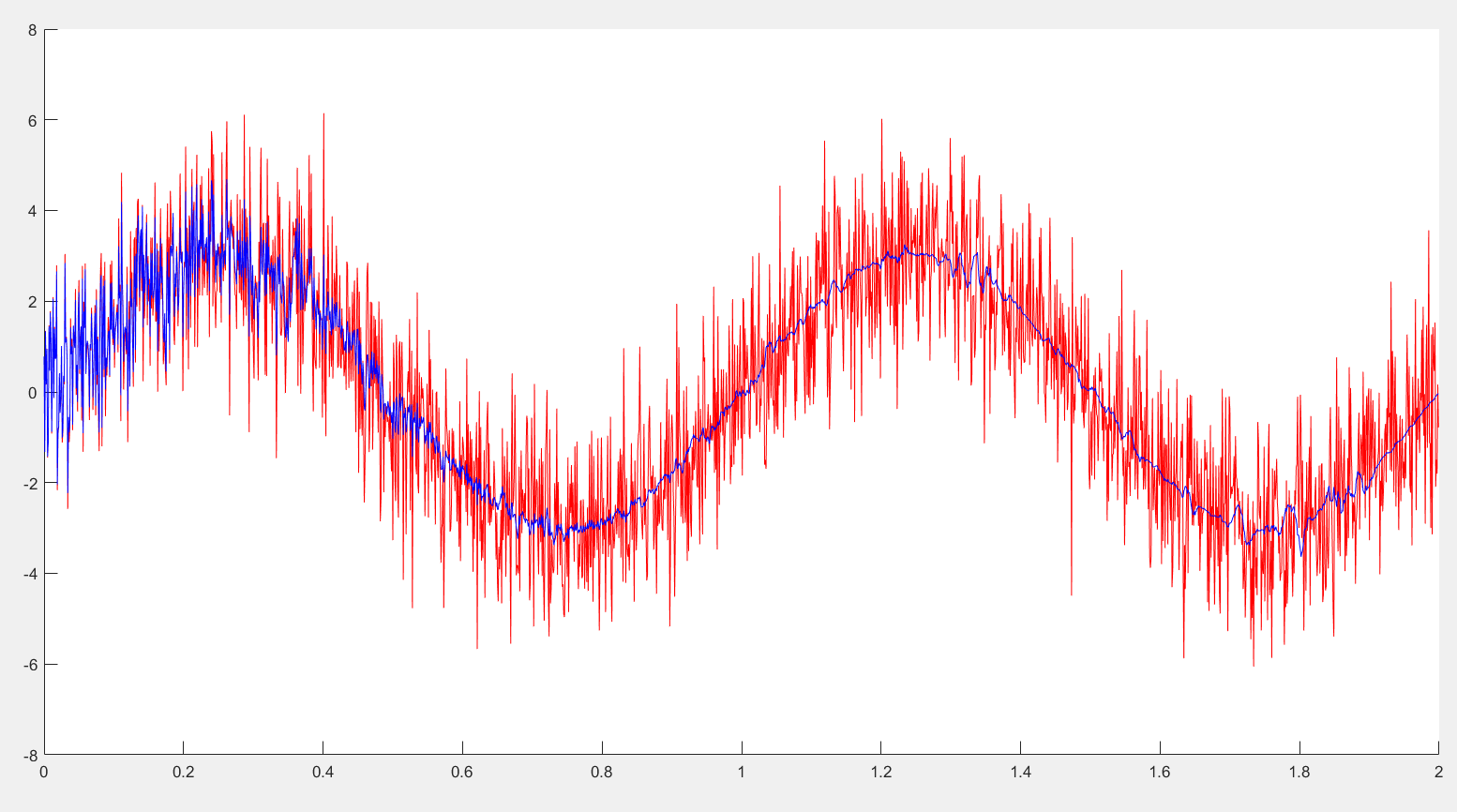
时域上可以看出基本上可以在混有热噪声的环境中恢复出1Hz的有用信号,杂波信号得到有效抑制
- 频域上
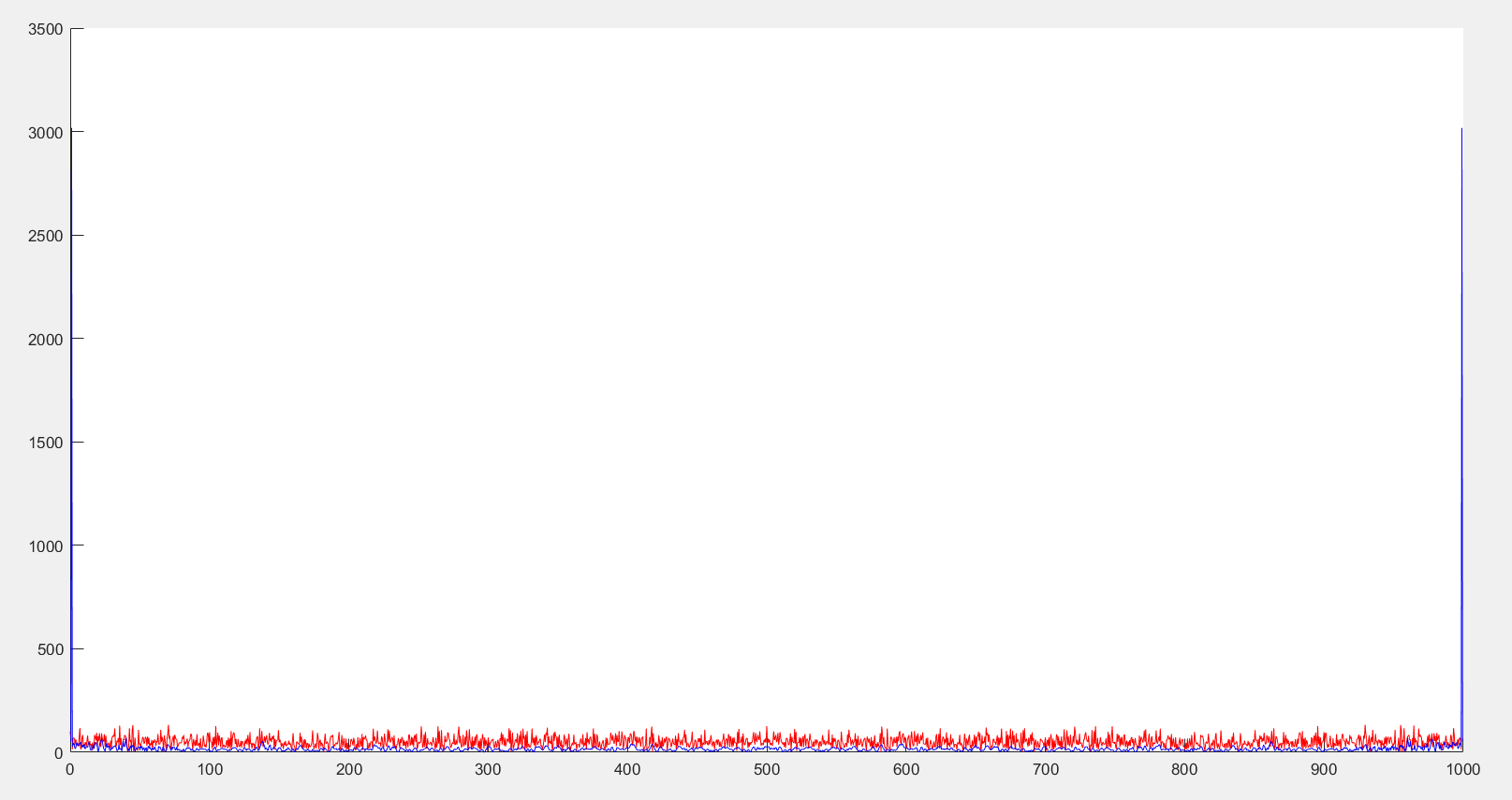
频域上也可以看出噪声信号得到了有效的衰减
滤波器优势
- 针对于传统滤波器无法处理的热噪声,LMS自适应滤波器可以有效的通过学习,训练然后从有用信号抵消热噪声
- 滤波器的参数便于调节,相比于传统的数字滤波器,每调整滤波器阶数都需要修改滤波器的结构,代码的重复利用性不高,而LMS自适应滤波器仅需要修改输入窗口大小M即可调整滤波器阶数
- 因为LMS学习的是噪声信号,然后滤除,不关心有用信号的特性,适合于对未知信号的提取

