问题提出

• 求解定积分，首先想到牛顿莱布尼兹公式计算

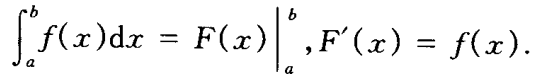
• 但是并不是所以被积函数都有原函数
• 由积分中值定理说明存在性

• 可以看作平均高度
• 其他近似
• 左矩阵公式

• 右矩阵公式

• 中矩阵公式

• 梯形公式

• Simpson公式

• 可以看作是（三个点的线性组合）*（b-a）
• 因此

机械型积分公式

• 设

• 因此积分可以看作是一系列数值的线性组合
• 其中,H称为求积系数，x称为求积节点，它们不依赖于f(x)的具体形式，E称为求积余项(或误差)

• 所谓数值积分问题,就是要通过某种途径确定H及x，并使得Q(f)逼近I(f)达到所要求的精度

  插值型积分公式

• 利用插值近似

• 其中设了

• 插值型积分，对Aj有固定要求
• Aj为求积系数，f(xj)为求积节点

• Aj只依赖于求积节点和积分区间，而与积分函数f(x)无关

  代数精度

• 存在定义

• 如果求积公式

• 对所有次数不超过r的多项式均能精确成立，而对于r + 1次的多项式至少有一个不能精确成立，则称该公式具有r次代数精度，或称该公式是r阶的，即：

• 举例
• 考察梯形公式的代数精度

• 考察Simpson公式的代数精度

• 存在定理
• 对于任意给定的n + 1个互异节点，总存在求积系数 ,使求积公式至少具有n次代数精度
• 且机械求积公式至少具有n次代数精度的充要条件是它是插值型的

，若为插值型，

等距节点Newton-Cotes公式

• 考察求积节点为等距的情形，将区间[a,b]划分为n等份,步长为,求积节点为

• 节点等距，计算求积系数带来方便
• 令，求积系数Hj可以表示成

• 令

• 称Cj为Cotes系数，于是得Newton-Cotes求积公式为

• 当n=1时

• 即为积分公式中的梯形公式
  • 当n=2时

• 即为积分公式中的Simpson公式
  • 当n=4时

• 即为Cotes公式

• 从确定求积公式系数的公式可以看出
• 因为被积函数是有理系数多项式,积分限为整数,所以Hj/h为有理数
• 因此Newton- Cotes公式可以写成

• 其中A为有理数而Wj均为整数
• 求积系数Hj=WjAh，Cotes系数
• Newton- Cotes公式系数表如下

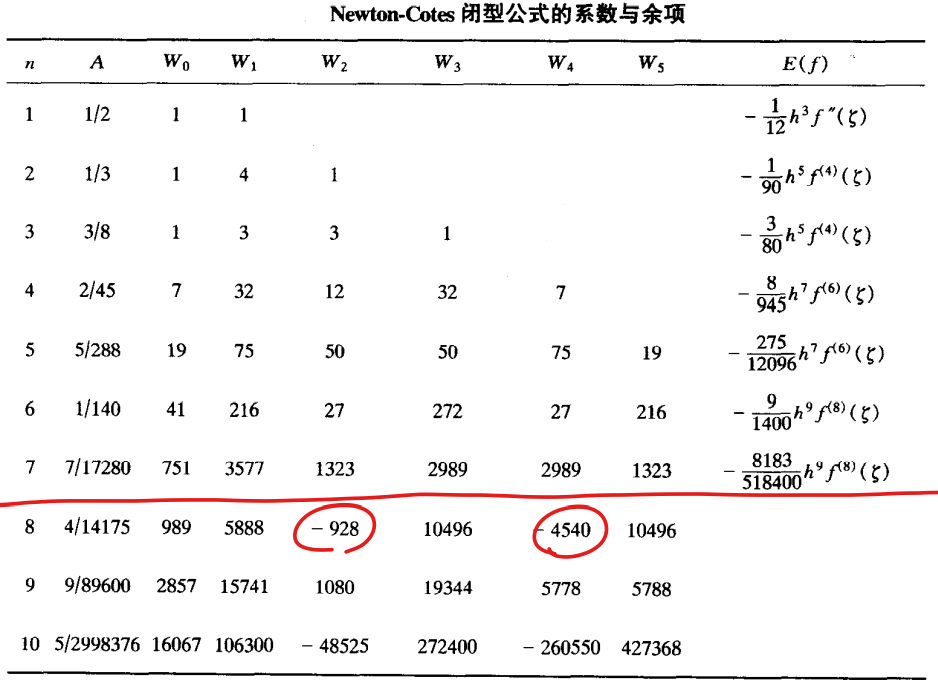
• Newton- Cotes公式的数值稳定性
• 下面考察Newton-Cotes公式的数值稳定性问题，即计算中的舍人误差对计算结果产生的影响问题
• 设精确值的计算值有舍人误差，即
• 则用，代替后所产生的误差为

• 设，当Cotes系数全正时，则有

• 即数值计算是稳定的.若Cotes系数有正有负时，因为成立

• 并且随着n的增大，变得越来越大,此时舍人误差对求积公式的影响就越坏

• 注意到只有当n≤7,n=9时,Cotes系数才是全正的,所以高阶Newton- Cotes公式是很少用

• Newton- Cotes公式的余项

• 定理：Newton- Cotes公式至少有n阶精度
• 当n是奇数时，r=n
• 当n是偶数时，r=n+1
• 因此有n=3和n=2时精度相同，没有必要计算n=3
• Newton-Cotes 公式至少具有n次代数精度，如果n是偶数,则其代数精度能提高到n + 1次

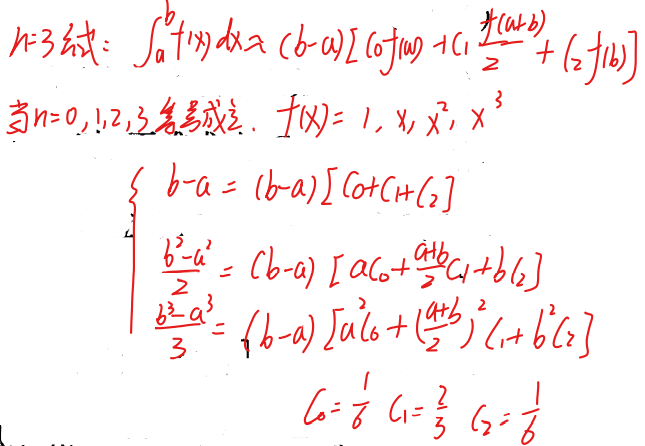
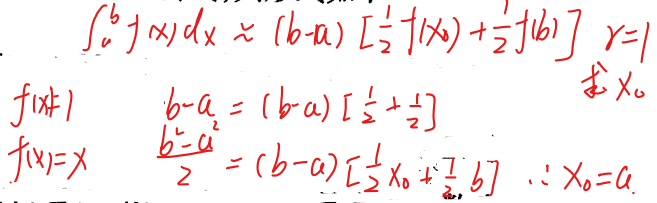
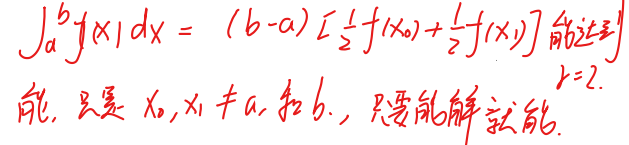
• 余项计算
• 下面给出几个低阶的Newton-Cotes公式的余项（其中）

复化的Newton-Cotes公式

• 对一般的插值型求积公式来说，并非对任何被积函数f(x)，当n→+∞时，余项En(f)都收敛于零
• 这就是机械求积的收敛性问题
• 另一方面又由于高阶的Newton-Cotes公式数值计算不稳定
• 所以人们不能企图通过增大n的途径来取得高精度的求积结果
• 为了改善求积精度，可以采用复化求积的思想
• 将积分区间[a,b]划分成若干个子区间,在每个子区闻上,用低阶的Newton-Cotes公式进行数值求积
• 然后将每个子区间上的数值求积的结果求和就得到整个区间[a,b]上的数值积分

• 最简单又最常用的办法是将区间[a ,b]分成n等份,步长，分点为，有时为了使用方便，取区间的等分数,这时步长，分点为

• 复化梯形公式

• 将区间n等分,在每个子区间上应用梯形公式，则有

• 称其为复化梯形公式.这里Tn的下标表示将区间[a,b]分成n等份
• 进一步，将区间2n等分，即把区间变为两个子区间,,
• 在每个子区间上应用梯形公式，便得到2n等分复化梯形公式

• 复化梯形公式的余项

• 复化Simpson公式
• 将区间[a ,b]分成n等份,步长，在每个区间上应用Simpson公式，则有

• 注意可以与复化梯形公式建立联系

• 得到

• 复化Simpson公式的余项

• 复化Cotes公式

• 得到递推公式

• 复化Cotes公式的余项

• 可证明复化的Cotes公式都是收敛的
• 例题
• 利用复化梯形公式计算积分

Romberg积分法

• 令梯形公式的值Tn=T(h)
• 可以证明复化梯形公式的值T(h)与积分值I(f)之间存在Euler -Maclaurin求和公式

• 即有

• 由梯形公式的简单组合可以得到比更高阶的求积公式

• 则逼近的阶为，这个算法称为数值积分的Romberg方法
• 实际上，便是复化的Simpson方法, 是复化的Cotes方法
• 当m> 2时,T(h)与复化的Newton-Cotes公式之间就没有直接关系了
• 令,即将积分区间[a,b]分成等份, 表示将区间等分后应用复化梯形公式的数值积分值，即T(h),再应用上连式就产生了Romberg 序列
• 现将Romberg方法综述如下:
  • 第一步,在[a,b]区间上，应用梯形公式求得

• 第二步,将区间[a,b]对分，应用复化梯形公式求得 ,并按公式

  - 求得Simpson公式的值。置i = 1 ,转第四步

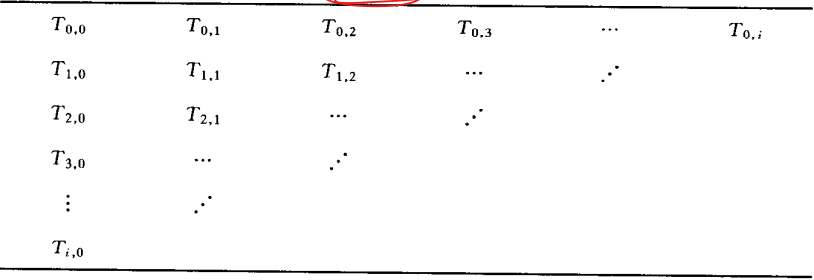
• 第三步,对区间[a,b]作等分,记相应的复化梯形公式求得值为然后按下式构造新序列

• 由此求得

• 第四步,若(ε是事先给定的精度),则计算停止,输出
• 否则用i + 1代替i,转入第三步.

• 由于上述方法每次把区间再对分一次,Romberg方法又称为数值积分逐次对分加速收敛法
• 计算过程公式列出如下

• Romberg积分法高速有效，易于编制程序，适合于计算机计算.
• 但它有一个主要缺点是,每当把区间对分后，就要对被积函数f(x)计算它在新分点处的值
• 而这些函数值的个数是成倍地增加的
• 例题

Gauss求积公式

• 当把求积节点xj和求积系数Hj均作为未知参数时，适当选择这些参数有可能使得求积公式具有2n+1次代数精度
• 如果求积公式具有2n + 1次代数精度，则称该公式为Gauss求积公式，相应的求积节点xj称为Gauss点
• 求积公式为Gauss公式的充分必要条件是在[a,b]上关于权函数与所有不超过n次的多项式正交即

• 存在定理：求积节点为n + 1个的机械求积公式的代数精度r不能超过2n + 1
• n + 1个求积节点的插值型求积公式的代数精度r满足

• 数值计算始终稳定
• Gauss求积公式也可以复化，过程基本相同