1. 卫星星座设计

• 多卫星构成系统
• 以最少数量实现对指定区域的覆盖

• 卫星星座类型

  • 极/近极轨道星座
  • 倾斜圆轨道星座（Delta和Rosette）
  • 共地面轨迹星座
  • 赤道轨道星座
  • 混合轨道星座

    1.1 极轨道星座

• 每个轨道面有相同的固定的倾角90°

• 每个轨道的卫星数目相同
• 每个卫星的轨道高度相同
• 所有的轨道平面在南北极形成两个交叉点
• 星座卫星在高纬度地区密集，在低纬度地区稀疏

• 轨道间隔存在不同

  1.1.1 卫星覆盖带

  

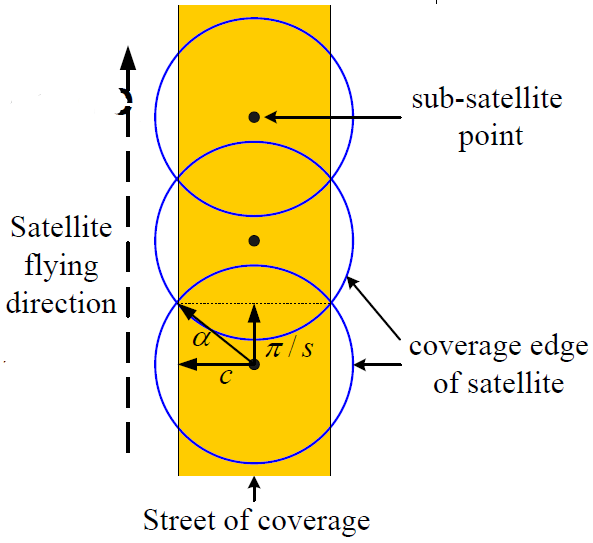
• 半覆盖宽度

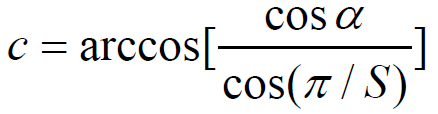
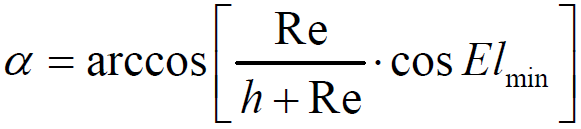
• 星座

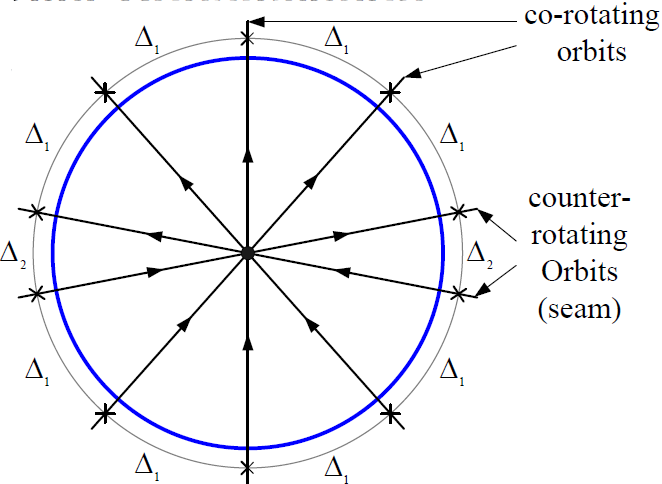
• 如图5个轨道组成的星座
• 由于存在逆向飞行现象，星座的第一个和最后一个轨道面的间隔小于其它相邻轨道面的间隔
• 相邻轨道面的几何覆盖

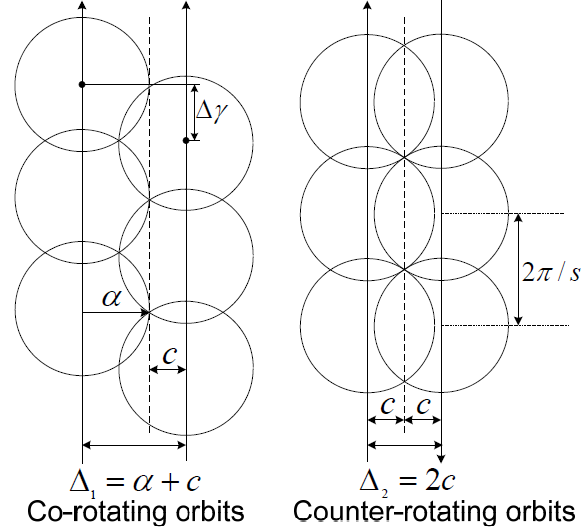
• 顺行轨道面间的升交点经度差
• 逆行轨道面间的升交点经度差

• 相邻轨道面相邻卫星间的相位差

  1.1.2 卫星覆盖条件

• 全球覆盖条件：

• 
• 球冠覆盖条件：

• 

  1.2 近极轨道星座

• 倾角接近但不等于90°，80-100°

• 覆盖带设计方法仍然适用

  1.3 倾斜圆轨道星座

  1.3.1 Delta星座

  

• 高度和倾角相同的圆轨道

• 轨道面升交点在参考平面内均匀分布

• 卫星在每个轨道平面内均匀分布

• 星座标识法

• Delta星座可以用一个3元参数组完整描述 T/P/F
• T：星座卫星总数
• P：轨道平面数量
• F：相位因子，取值0 - P-1
• 相位因子确定相邻轨道面相邻卫星间的相位差
• 例题

1.3.2 Rosette星座

• 玫瑰星座

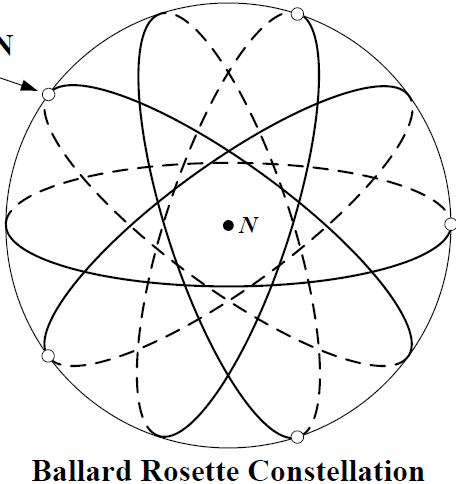
• 圆轨道
• 所有轨道的高度和倾角相同
• 轨道面升交点在参考平面内均匀分布
• 卫星在轨道内均匀分布

• 卫星在轨道内的初始相位与该轨道面的升交点角成正比

• 星座标识，3元参数组（N，P，m）

• N：星座卫星总数
• P：轨道平面数量

• m：协因子，影响卫星在天球上的初始分布以及星座图案在天球面上的推移速度

• 如果m是整数，意味着星座每轨道面仅有一颗卫星

• 如果m是一个不可约分数，意味着每个轨道平面上有S=N/P颗卫星，且m的分母值为S

1.3.3 Rosette与Delta的等价

• Delta星座的相位因子F与玫瑰星座的协因子满足如下关系

• 例题

• Rosette星座与Delta星座的对比
• 共同点
  • 所有卫星的轨道倾角相等，全部卫星在同一轨道高度，每个轨道上的卫星的数目相同且均匀分布
• 不同点
  • 评价标准不同：Delta星座从地面仰角出发，Rosetta从星下最大覆盖性能出发
  • 相邻轨道相位差确定方法不同：Delta星座由相位因子F决定，Rosette由协因子m决定

1.4 共地面轨迹星座

• 星座中所有卫星沿相同的地面轨迹运动，心下点轨迹相同
• 由于自转影响，轨道面升交点在赤道平面内的分布不一定是均匀的，轨道面会发生变化
• 星座中的卫星在特定的区域上空相对密集
• 为使得地面轨迹与地面保持相对固定的状态，轨道应采回归或准回归轨道
• 回归/准回归轨道是卫星的星下点轨迹在M个恒星日，围绕地球旋转L圈后重复的轨道

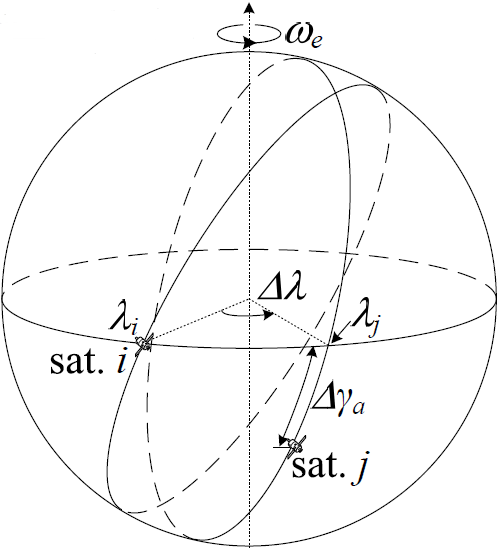
• 设计条件：

1.5 赤道轨道星座

• N颗卫星在特定高度的赤道轨道面上均匀分布

1.6 混合轨道卫星

2. 星际链路

2.1 星际链路的分类

• 面内星际链路
  • 卫星间的相对运动几乎为零，星际链路天线的指向角固定，无需跟踪
• 面间星际链路
  • 卫星间存在相对运动，需要采用跟踪天线

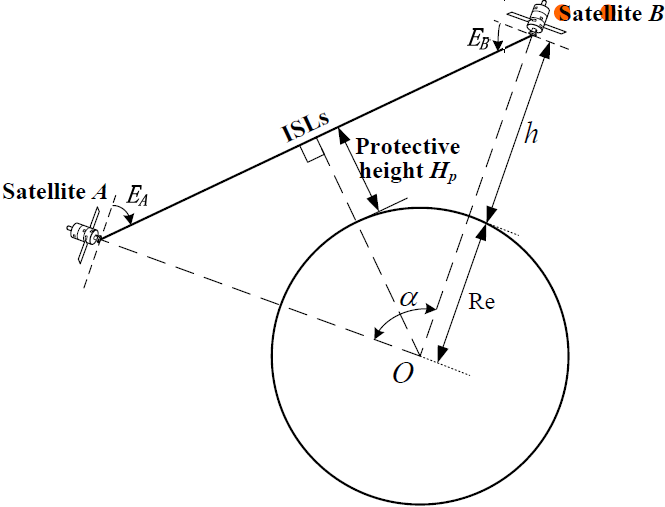
• 层间星际链路

  • 存在相对运动会发生链路的重建，需要跟踪天线

    2.2 星际链路的计算

    

• 卫星高度相同

• 仰角计算

• 距离计算

• 最大地心角

• 最大距离

• 例题

3. 系统体系结构

• 方案1：透明转发式卫星，无星际链路，依赖地面网络连接信关站
  • 全球星系统
• 方案2：无星际链路，使用GEO提供信关站之间连接
• 方案3：使用星际链路实现卫星之间的互联
  • 铱系统
• 方案4：双层卫星网络构建混合星座结构