1. 平稳随机过程
，随机过程X(t)的n维概率密度满足
则X(t)为严平稳（狭义平稳）随机过程
- 任意维统计特性均与时间起点无关，在任何时刻或时间区间计算的统计结果均相同
1.1.1 一维严平稳过程
- 一维概率密度和数字特征均与时间无关
1.1.2 二维严平稳过程
- 二维概率密度和自相关只与
的时间间隔
有关，而与时间起点无关 
1.1.3 严平稳的判断
- 正向判断困难，n维概率密度难求
- 反例判断，判断非严平稳过程
- 检验矩特征：
- 检验数字特征：对于任意时刻
，
是否具有相同的统计特征
- 检验矩特征：
1.2 宽平稳过程
1.2.1 判定条件
- 数学期望是常数，即与时间无关
- 自相关只与时间间隔有关
- 信号功率有限或二阶矩存在
1.2.2 与严平稳的关系
- 严平稳过程一定是宽平稳的，反之不一定成立
- 这主要是因为严平稳是从过程的根上，即概率密度定义的，而宽平稳只是从数字特征上定义
- 高斯过程中，严平稳与宽平稳可以等价
2. 平稳随机过程相关性分析
2.1 平稳随机过程相关函数的性质
- 偶对称性
- 功率信息
- 最大值
- 平稳过程自相关函数的最大值在
时 
- 注：自相关函数也可能在
处取得最大值
- 平稳过程自相关函数的最大值在
- 非负定性
- 任意实数
- 任意实数
- 周期一致性
- 周期为
的随机过程，即
- 其自相关函数也是周期为的函数
- 周期为
- 周期分量一致性
- 若平稳过程含有一个周期分量，则其自相关函数也可能含有同周期的周期分量
- 均值信息
- 若平稳过程中不含有任何周期分量
- 数字特征
- 若平稳过程中不含有任何周期分量
- 几何图形
- 平稳过程自相关函数的图形中一定不会出现‘平顶’，‘垂直边’或在幅度上的任何不连续
- 即不含阶跃因子
- 平稳过程自相关函数与功率谱密度是傅氏变换对
2.2 平稳随机过程的自相关系数
自相关系数：归一化的自相关函数，描述平稳随机过程X（t）的关联程度
2.3 平稳随机过程的自相关时间
2.3.1 自相关时间的概念
与
的相关程度减弱
称为相关时间
2.4 两个随机过程的联合平稳
2.4.1 联合严平稳
两个随机过程X（t）和Y（t）的任意n+m维联合概率分布不随时间平移而变化
2.4.2 联合宽平稳
两个随机过程X（t）和Y（t）满足：
- X（t）和Y（t）分别是宽平稳随机过程，即分别满足宽平稳三大条件
- X（t）和Y（t）的互相关函数仅与两者的时间差有关
镜像关系
- 要和奇函数偶函数区分开
- 非零点取值和零点取值的关系
特殊取值代表的含义
两个随机过程联合平稳时，互协方差为
- 互相关系数定义为
- 又称作归一化互相关函数或标准互协方差函数
3. 各态历经随机过程
3.1 存在问题
- 随机过程概率分布未知，需大量重复观察实验，样本函数
- 从一个样本函数中提取整个过程统计特征的信息
- 各态历经随机过程的提出，一个样本函数做时间平均能在概率意义上趋近于其统计平均
3.2 各态历经
- 任一个样本函数经历了过程的各种可能状态，
- 从各态历经过程中任一个样本函数中可以提取到整个随机过程统计特性的信息
- 各态历经必然平稳,而平稳不一定各态历经
3.3 严各态历经
- 一个随机过程的各种时间平均均收敛于相应的统计平均
- 则称具有严格遍历性，为严各态历经过程
3.4 宽各态历经
满足
- 即时间平均=统计平均
- 时间相关=统计相关
3.5 联合宽各态历经
满足
- 即时间互相关=统计互相关
3.6 各态历经过程一二阶矩的物理意义
- 期望: 过程的直流分量
- 均方值:过程的总平均功率
- 方差:过程的交流平均分量
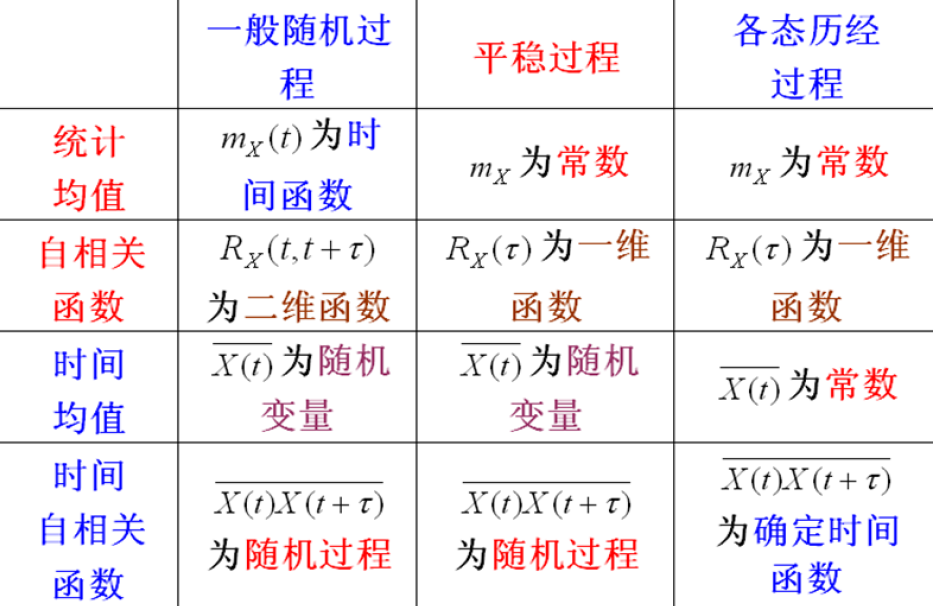
4. 各种随机过程的统计特征
若有收获，就点个赞吧
0 人点赞
