3.1 引言

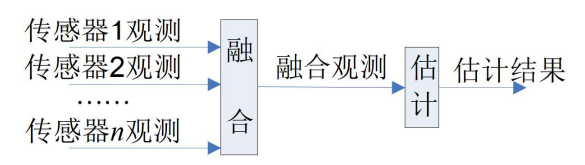
• 在多传感器信息融合系统中，就位置(空间)级融合系统的结构而论有集中式、分布式结构
• 所谓信息融合主要有两项任务
• 其一是点迹-航迹互联和/或航迹与航迹关联问题

• 其二是目标状态的估计和/或航迹融合问题

  3.2 集中式多传感器信息融合系统中的状态估计

  3.2.1 单传感器的状态估计

• 一般的监视和跟踪系统中

• 其目标运动和传感器测量方程都是线性的，过程与测量噪声是相互独立的，并且系统模型中不含控制项

• 为了讨论问题的方便，下面再次描述目标运动、传感器测量和单传感器 Kalman 滤波方程

• 设在离散化状态方程的基础上目标运动规律可表示为

• 其中
• 是 k 时刻目标的状态向量
• 是零均值白高斯过程噪声向量
• 是状态转移矩阵
• 是过程噪声分布矩阵
• 初始状态 X（0）是均值为 μ 和协方差矩阵为 P0 的一个高斯随机向量，且
• 定义两个集合，设

• 其中，
• M 是局部节点数（区域数）, Nj 是局部节点 j 的传感器数。
• 局部节点 j 传感器 i 的测量方程可表示为

• 其中，
• 是测量矩阵
• 是均值为零相互独立的高斯序列，且

• 是正定阵，同时

• 现在考虑局部节点估计与传感器测量位于不同坐标系的情况

• 设传感器 i 在局部节点笛卡尔坐标系中的三个位置分量为
• 并假定目标的位置坐标分量 (x, y, z轴分量) 包含在测量向量中
• 于是，令

• 为传感器 i 的 状态坐标偏移量 在局部节点 j 笛卡尔坐标系中的增广向量
• 那么传感器 i 在局部节点 j 笛卡尔坐标系中 k+1 时刻的观测为

• 综合状态估计理论中的 Kalman 滤波方程，局部节点 j 中的第 i 个传感器的 Kalman 滤波方程为

• 其初始条件为

  3.2.2 集中式多传感器状态估计

• 节点 j 处的局部广义测量矢量

• 于是局部广义测量方程为

• 这里

• 且有

• 其中

• 而

• 设局部节点 j 在融合中心坐标系的位置为，定义：

• 为局部节点 j 位置坐标的增广向量，则节点 j 在融合中心坐标系中 k+1 时刻的局部广义测量向量为

• 将离散 Kalman 滤波理论应用于构成的线性系统，则局部节点的集中状态估计方程为

• 将上式代入

• 可得

• 其初始条件为

• 由此得到了二级多传感器系统的集中状态估计

  3.3 分布式多传感器信息融合系统中的状态估计

• 这里所说的分布式多传感器系统是指如图所示的结构，也称作分级或二层结构。对这种系统的状态估计通常称为航迹融合或合成。这种结构模型的状态估计以局部节点 j(j∈U) 为例以定理的形式给出。

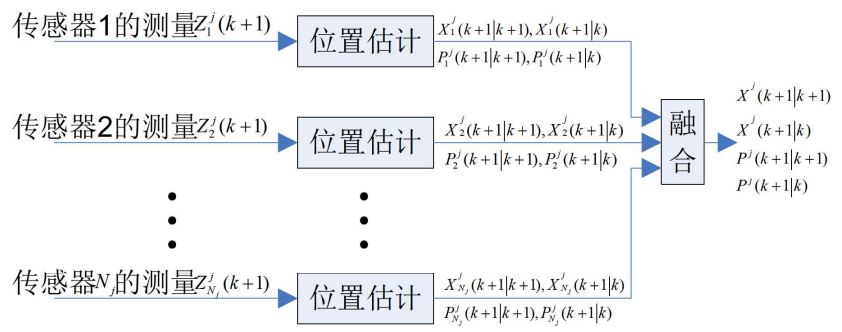
• 定理1 由方程

• 给出的是传感器级状态估计，其 Nj 个传感器在局部节点 j 的最优航迹合成解的一种形式为

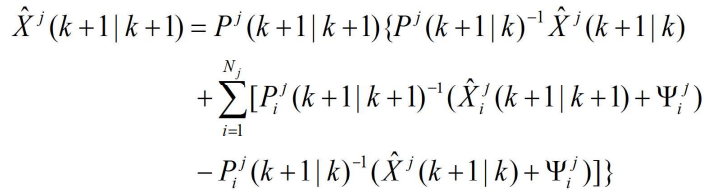
• 证明：展开下式右侧

• 合并有

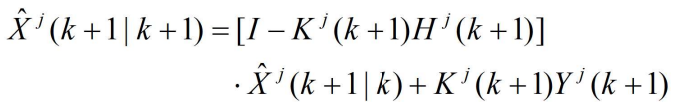
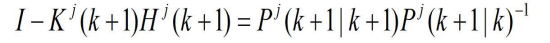
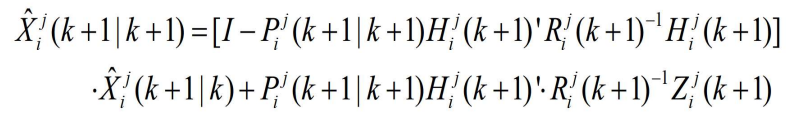
• 这里隐含假定所有出现的矩阵求逆都是存在的，并且P0是非奇异的

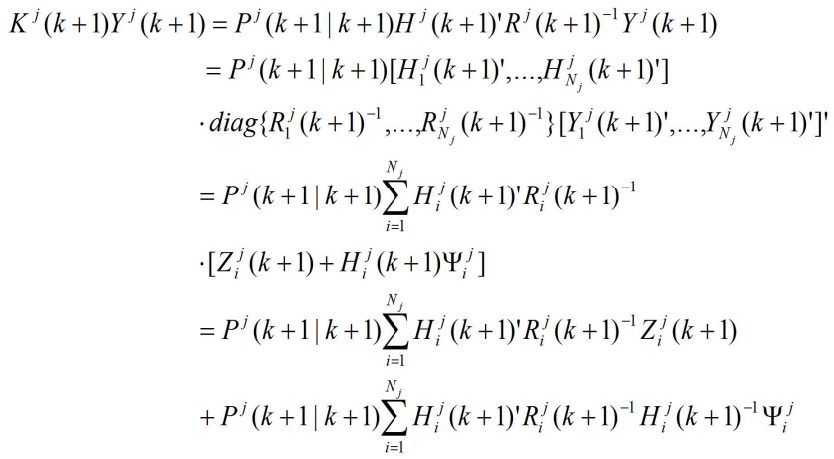
• 为了用传感器级的状态估计表示局部节点 j 的状态估计，消去

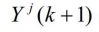
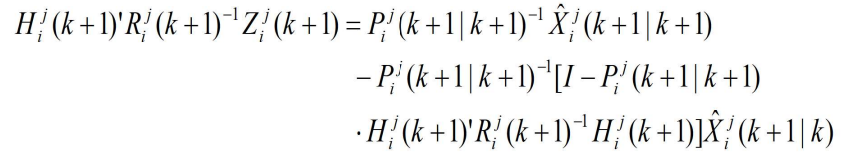
• 对传感器 i 来说，有类似的表达式

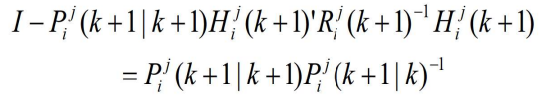
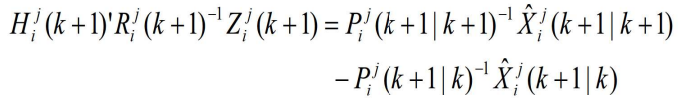
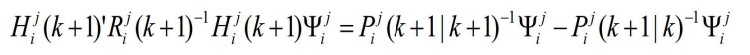
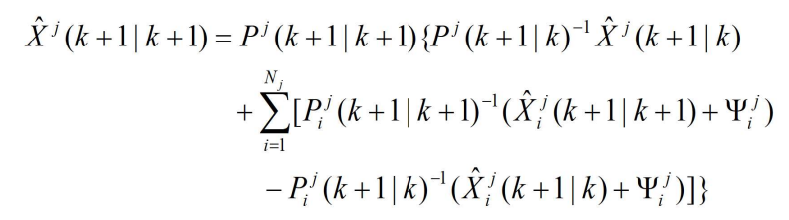
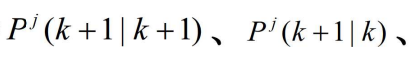
• 方程式中的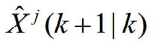分别由前式给出，而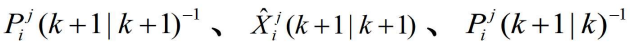和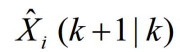则来自于传感器级的状态估计方程