问题产生

在接触各种传感器返回的数据的过程中，会遇到各种各样的信号干扰，大多在时域上的体现为信号的毛刺，或信号的包络。我们想要设计滤波器让原始信号通过后得到想要的稳定的真实的数据，就需要分析信号的特征。往往在时域上很难直观的看到噪声和真实数据的区别，而信号的特征在频域上就会较为明显。因此需要对信号做频域上的分析。

使用工具

matlab软件

编程实现

  1. %数据源为三种频率的正弦信号
  2. N = 100;                        %数据个数
  3. fs = 1000;                    %采样频率(Hz)
  4. Ts = 1/fs;                    %采样周期(s)
  5. Time = (0:N-1)*Ts;    %时域x坐标轴(s)
  6. Freq = (0:N-1)*fs/N;%频域x坐标轴(Hz)
  8. %三种频率的实验信号
  9. f1 = 50;                        %信号1频率Hz
  10. f2 = 100;                        %信号2频率Hz
  11. f3 = 300;                        %信号3频率Hz
  12. Input_1 = sin(2*pi*f1*Time);
  13. Input_2 = 0.2*sin(2*pi*f2*Time);
  14. Input_3 = 0.3*sin(2*pi*f3*Time);
  15. Input_All = Input_1+Input_2+Input_3;%信号叠加

这里解释一下时域和频域的坐标轴设置原理
时域：采样N个点，点与点的间隔是采样周期，因此坐标轴应设置为 [0 Ts 2Ts 3Ts …… (N-1)Ts]，共N个点
频域：时域上的N个点，经过N点傅里叶变换到频域上时，仍然得到N个点，由采样定理得可知，当对信号采样时，信号的频域将按照采样频率做周期延拓，因此频域上信号的周期为fs，频域上点与点的间隔即为fs/N。频域上的坐标轴应设置为 [0 fs/N 2fs/N 3fs/Ns …… (N-1)fs/N]

  1. %三种信号的时域图
  2. figure(1);
  3. hold on;
  4. plot(Time,Input_1,'y');
  5. plot(Time,Input_2,'b');
  6. plot(Time,Input_3,'g');
  7. xlabel('t/s');
  8. ylabel('A');
  9. %三种信号叠加的时域图
  10. figure(2);
  11. hold on;
  12. plot(Time,Input_All,'r');
  13. xlabel('t/s');
  14. ylabel('A');

用时域坐标轴绘制时域上的信号波形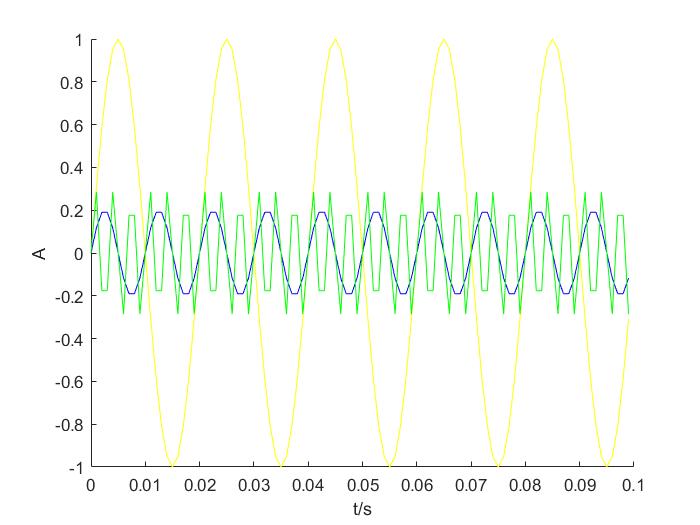
1.jpg

  1. Input_All_fft = fft(Input_All,N);
  2. figure(2);
  3. hold on;
  4. xlabel('f/Hz');
  5. ylabel('A');

分别对三个频率的信号叠加后的信号做傅里叶变换，得到频域序列，再结合频域坐标轴，即得到信号的频域

1.jpg
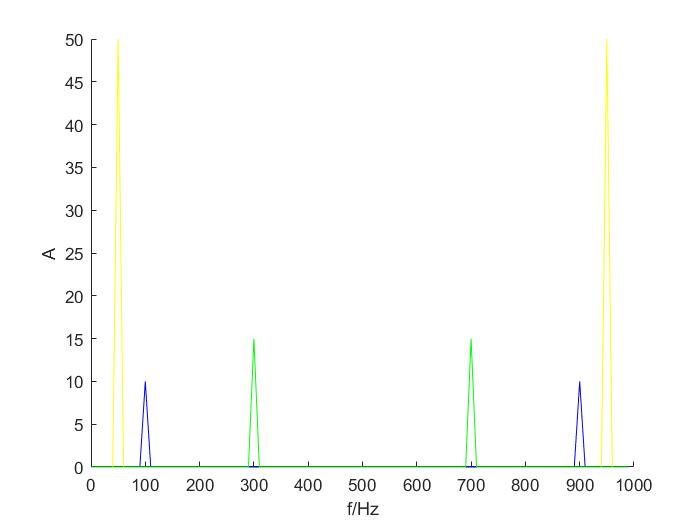
从频域上明显可以看到叠加信号中存在50Hz，100Hz，300Hz的信号

可能会有疑问，700Hz，900Hz和950Hz上也有波形，为什么不能说明叠加信号中也存在它们呢？
我们回头分析，采样频率为1000Hz，由奈奎斯特采样定理可知，能有效采样的信号频率不得大于fs/2，即500Hz，因此[0，500]Hz为频域的有效区间，大于500Hz的地方实际上是复频域，和正频域[0，500]Hz对称。同时由这个图也可以印证采样定理（当对信号采样时，信号的频域将按照采样频率做周期延拓），因此大于500Hz的波形是周期延拓后的前半周期。
在分析时只需分析图形中的前一半即可。

后续完善

  1. % draw frequence domain
  2. %数据源为三种频率的正弦信号
  3. N = 100;            %数据个数
  4. fs = 1000;          %采样频率(Hz)
  5. Ts = 1/fs;          %采样周期(s)
  6. Time = (0:N-1)*Ts;  %时域x坐标轴(s)
  7. Freq = (-(N-1)/2:(N-1)/2)*fs/N;%频域x坐标轴(Hz)
  9. %三种频率的实验信号
  10. f1 = 50;            %信号1频率Hz
  11. f2 = 100;           %信号2频率Hz
  12. f3 = 300;           %信号3频率Hz
  13. Input_1 = sin(2*pi*f1*Time);
  14. Input_2 = 0.2*sin(2*pi*f2*Time);
  15. Input_3 = 0.3*sin(2*pi*f3*Time);
  16. Input_All = Input_1+Input_2+Input_3;%信号叠加
  18. %三种信号的时域图
  19. figure(1);
  20. hold on;
  21. plot(Time,Input_1,'y');
  22. plot(Time,Input_2,'b');
  23. plot(Time,Input_3,'g');
  24. xlabel('t/s');
  25. ylabel('A');
  26. %三种信号叠加的时域图
  27. figure(2);
  28. hold on;
  29. plot(Time,Input_All,'r');
  30. xlabel('t/s');
  31. ylabel('A');
  33. Input_All_fft = fft(Input_All,N);
  34. figure(3);
  35. hold on;
  36. Input_All_fftshift = fftshift(Input_All_fft);
  37. plot(Freq,abs(Input_All_fftshift),'r');
  38. xlabel('f/Hz');
  39. ylabel('A');