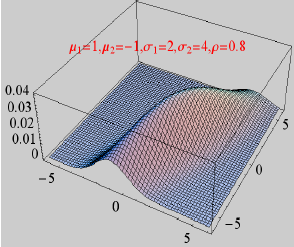
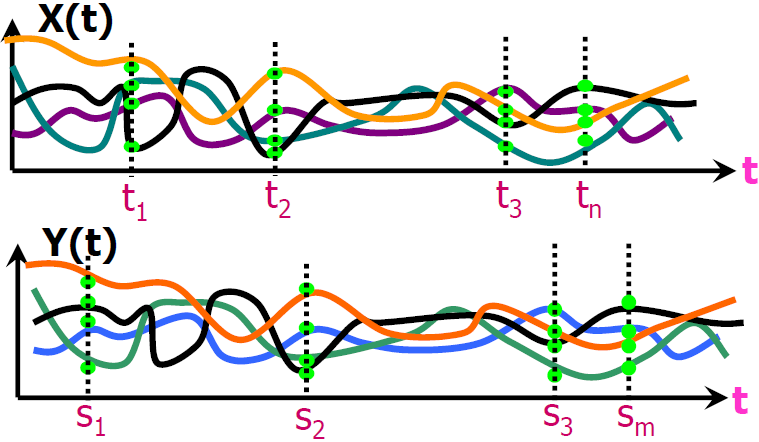
随机过程的定义

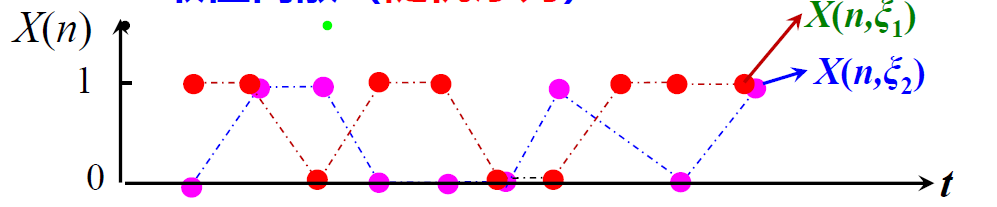
离散随机过程

随机变量序列的集合

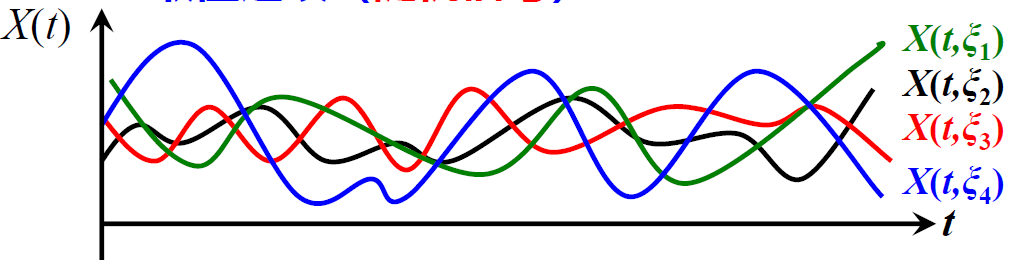
连续随机过程

样本函数的集合

样本空间

是实验时间和试验样本的二维函数

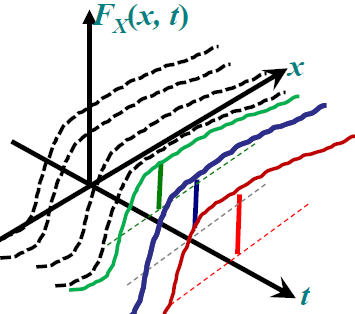
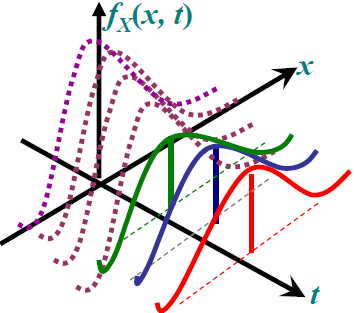
随机过程一维CDF，pdf，CF

一维概率分布

一维概率密度

一维特征函数

一维分布只能反应随机过程在某一孤立时刻的分布规律，不能揭示其整体分布规律
计算时，仅需将时间固定，视其为一个常量，即可按照随机变量处理

随机过程二维CDF，pdf，CF

二维概率分布

二维概率密度

二维特征函数

n维类推

随机过程的数字特征

计算方法：先把时间固定，然后用随机变量的分析方法来计算

数学期望

均方值

即二阶原点矩

方差

即二阶中心矩

离散随机过程的数字特征即把上述积分转变为求和
以上数字特征仅描述了各个孤立时刻的特征，不能反映过程内部变化快慢，相关性强弱的状况

自相关函数

二阶混合原点矩

协方差函数

二阶混合中心矩

注：求自身自相关函数即为均平方，对自身求协方差即求方差
自相关函数和协方差函数均描述了随机过程任意两个时刻的状态之间的内在联系
相关的概念表征了随机过程在两时刻的关联程度，进而说明了随机过程起伏变化的快慢

自相关系数

联合随机过程

描述两个随机过程之间的内在联系

n+m维联合概率分布

n+m维联合概率密度

互相关函数

• 实信号

• 复信号

互协方差函数

• 实信号

• 复信号

互相关系数

正交

不相关

统计独立

相互关系

• 一般情况

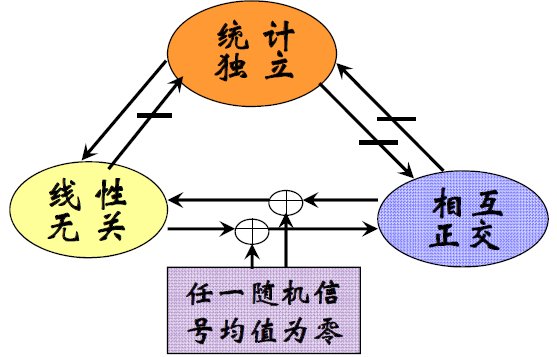
• 高斯信号

• 高斯信号且有一个均值为零