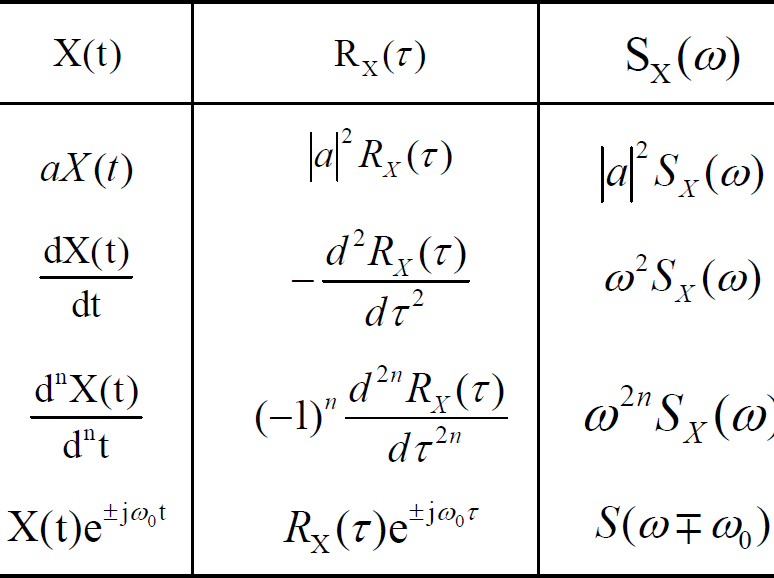随机信号的频域分析

• 不能直接应用傅里叶变换
• 随机信号持续时间无限长，总能量不是有限的
• 随机信号不满足绝对可积和能量有限这两个条件
• 必须经过处理

• 随机信号属于功率型信号，其能量谱不存在，但功率谱存在

  随机信号的功率谱

• 单个样本函数

• 对原随机信号截断
• 截断函数(-T~T)的傅里叶变换

• 截断函数的能量

• 样本函数的平均功率

• 功率谱密度

• 样本空间所有函数
• 功率谱密度

• 时域与频域的关系
• 平均功率

• 平均功率即为功率谱密度的积分

  维纳辛钦定理

• 平稳随机信号,自相关函数可积,则自相关函数和功率谱密度构成一对傅里叶变换

• 功率谱密度是自相关函数的傅里叶变换

功率谱密度性质

• 非负性

• 实值性

• 偶对称性

由偶对称性可改写功率谱密度和自相关函数的求法

• 绝对可积性

• 实轴无极点性

  • 功率谱密度可以表示为一个有理函数时
  • 式中分母无实根（实轴上无极点）
  • 因为要满足可积性

    维纳辛钦定理推广

• 定理存在局限

• 自相关函数和功率谱密度绝对可积
• 导致数学期望必须为零，平均功率必须为零

• 即不能含有直流信号和周期信号

• 定理推广

• 借助函数表示直流信号和周期信号

等效功率谱带宽

• 相关性越弱，功率谱越宽平；相关性越强，功率谱越陡窄
• 等效功率谱带宽定义：

• 即等面积矩形宽度的一半

• 物理意义：刻画随机信号起伏的最高频率（频繁程度）

  时间带宽积

  

• 相关时间和功率谱带宽成反比

• 功率谱带宽宽，信号相关时间短，变化频繁

  常用变换对

  

  互功率谱密度

• 两个实平稳随机过程

• 互功率定义为

• 互功率谱密度

• 互功率谱和互功率满足

• 互功率谱密度与互相关函数

互功率谱性质

• 不等式特征
  • 
• 交叉偶对称及交叉共轭对称性
  • 
• 实部偶对成性
• 虚部奇对称性
• 正交互谱零值性
  • 若与正交，则它们的互功率谱为零
  • 

• 不相关互谱冲击性

  • 若与不相关
  • 
  • 

    高斯过程

• 任意时刻，随机过程的任意n维随机变量服从高斯分布

• 广义平稳高斯过程：
  • 正态随机过程X(t)的均值和方差均与时间无关
  • 自相关函数只取决于时间间隔

• 性质：

  • 高斯随机过程的宽平稳等价于严平稳
  • 不相关等价于相互独立
  • 平稳随机过程 + 确定时间信号 = 高斯过程（不一定平稳）
  • 平稳高斯过程均方极限 = 高斯随机变量
  • 高斯过程积分/求导 = 高斯过程
  • 平稳高斯过程与导数的联合PDF仍为高斯分布
  • 高斯过程经过线性变换后仍满足高斯过程
  • 高斯过程通过线性系统仍是高斯过程

    白噪声过程

• 白噪声与高斯噪声

  • 高斯噪声：具有高斯分布的噪声，是从时域角度分析信号
  • 白噪声：功率谱为常数的随机过程，是从频域角度分析信号
  • 两者是从不同角度描述，定义方向不同，两者非互斥，一个信号可以兼具两种特征

• 均值为零，功率谱密度在整个频率轴上为非零常数的

• 自相关函数：

• 相关系数：

• 即说明不同时刻上不相关

• 等效带宽：

• 相关时间：

• 平均功率：

• 白噪声是理想化模型

带限白噪声

• 有限频率范围内功率谱密度均匀分布，值为
• 低通型带限白噪声

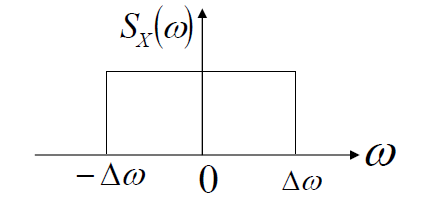
• 低通型带限白噪声自相关函数

• 带通型带限白噪声

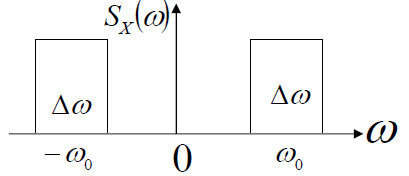
• 带通型带限白噪声自相关函数

色噪声

• 将各频率分量大小不同的噪声称为有色噪声

信噪比

相互关系