线性规划与凸优化概念

线性规划是在满足一组线性等式或不等式约束的条件下，使一个线性函数达到极值。
即，目标函数与约束均为线性的规划称为线性规划。

如果线型规划是凸优化的，凸优化是指在凸集上的凸函数规划，称为凸优化，又称之为凸规划

凸集：线性集合是凸集，其要求满足需要：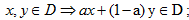

凸函数：线性函数是凸函数, 即：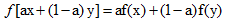

线型规划的矩阵形式为：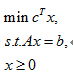

• 其中A称为约束矩阵。
• 不等式约束条件可以借助通过引入松弛变量，把不等式变为等式。

  优化问题基本表示

  优化问题是应用数学重要研究领域
  具体是研究在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称
  其一般数学模型为：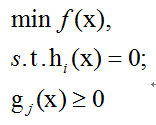
  
  在上式优化模型中

1. x为n维向量，为实际运用中的解
2. s.t.为英文subject to的缩写，表示受限于
3. f(x)称为目标函数，如上式，我们要求f(x)的最小值
4. h(x)为等式约束
5. g(x)为不等式约束

   优化问题分类

   根据目标函数与约束函数的不同形式，可以把最优化问题分为不同的类型

根据约束函数，可分为：无约束最优化，等式约束最优化，不等式约束最优化

无约束最优化问题：

• 通常给定一个初始的可行点x0，由这个可行点出发，依次产生一个可行点列
• x1,x2…xk,使得某个xk恰好是问题的一个最优解，或者该点列收敛到最优解
• 也就是选取一个可行的方向，再往这个方向行进，即下降算法
• 在迭代中，要求f(xk+1)<f(xk)。下降算法中基本的问题有两个：方向与步长
• 对于性能的衡量，也有：收敛于不收敛，局部最优与全局最优
• 常见的下降算法有：
  • 最速下降法
  • Newton法
  • 共轭方向法和共轭梯度法
  • 拟Newton法
  • Powell方向加速法等

有约束最优化问题：

• 可以通过拉格朗日乘数和KTT条件转化为无约束最优化问题
• 还可以采用其他一些流行的方法有：
  • 模拟退火
  • 遗传算法
  • 类免疫算法
  • 演化策略
  • 神经网络
  • 支持向量机等

根据目标函数与约束函数类型分类：

• 若f(x),h(x),g(x)都是线性函数，则称为线性规划
• 若其中至少有一个为非线性函数，则称为非线性规划

对于特殊的f(x),h(x),g(x)，还有特殊的最优化问题

• 如果目标函数为二次，约束全为线性：二次规划。
• 如果目标函数不是数量函数而是向量函数：多目标规划。

  优化问题求解方法

  总的而言，可以将优化求解方法分为解析法和直接法

可以通过一些数学知识来直接求解最优化问题的最优点，这种方法称为解析法
比如我们一阶函数求导得极值的方法。

所谓的最优性条件，也就是最优点满足的条件
然而，一般情况下，很难直接通过最优性条件求解最优化问题
但是最优性条件的研究，对于问题的求解以及判定结束状态都有帮助

例如，无约束优化的最优性条件为例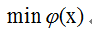

据微积分的知识，有如下结论：

参考自