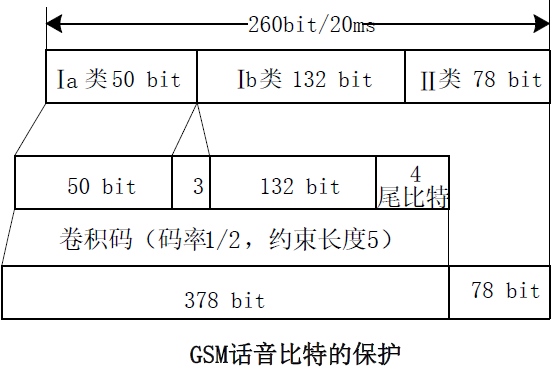
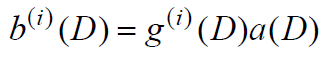3. 信道编码技术

  • 基本思想：
    • 引入可控制的冗余比特，使信息序列的各码元和添加的冗余码元之间存在相关性
    • 在接收端信道译码器根据这种相关性对接收到的序列进行检查，从中发现错误或进行纠错

  • 作用：

    • 尽量减小信道噪声或干扰的影响，改善通信链路性能

      3.1 概述

      传输信道常见噪声

  • 随机噪声：错误随机，序列中出现位置随机分布，相互独立，错误不会成片出现，一般由加性随机噪声造成

  • 突发错误：错误连串出现，在一个突发错误持续时间内，开头和末尾的码元错误
  • 混合错误：随机错误和突发错误混合

任何纠错码能力都是以冗余度为基础，存在代价

  • 频带利用率降低（信源速率不变提高信道传输速率，占用更大带宽）
  • 或者功率利用率降低（带宽不变，采用多电平调制，误码率不变要增大平均功率）

  • 或者设备变得复杂（交织编码）

    3.2 分组码

    3.2.1 分组码基本描述

  • 二进制分组码编码器

  • 输入为长度k的信息矢量a=(a,a……a)
  • 输出长度为n的码字C

【移动通信】抗衰落技术_信道编码 - 图1

  • 生成矩阵G（k×n）
  • 编码效率【移动通信】抗衰落技术_信道编码 - 图2
  • 输入矢量有2种，因此编码得到的码字也有2
  • 码字集合称为线性分组码(n,k)分组码

【移动通信】抗衰落技术_信道编码 - 图3

  • 校验矩阵（（n-k）×n）H
  • 也满足

【移动通信】抗衰落技术_信道编码 - 图4
信道编码可表示为由编码前的信息码元空间【移动通信】抗衰落技术_信道编码 - 图5到编码后的码字空间【移动通信】抗衰落技术_信道编码 - 图6的一个映射【移动通信】抗衰落技术_信道编码 - 图7

  • 如果f满足线性编码映射，则为线性编码
  • 如果是一一对应的，则为唯一可译线性编码
  • k为信息位数，n为码长
  • 线性指码组中码元之间的约束关系为线性
  • 分组指编码时将每k个信息位分为一组独立处理

线性分组码特征

  • 加法封闭性：码组集合中任意两个码组相加仍为集合中的一个许用码组
  • 全零序列是线性分组码中的一个码字
  • 码组集合中码组之间的最小码距等于某非零码字的最小码重

任意两个码字之间汉明距离的最小值称作码的最小距离，为dmin
dmin是衡量码的抗干扰能力（检、纠错能力）的重要参数，dmin越大，码的抗干扰能力就越强。

  • （n, k）线性分组码能纠正t个错误的充分必要条件是

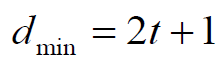
image.png

  • （n, k）线性分组码能发现接收码字中l个错误的充分必要条件是

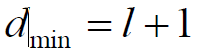
image.png

  • （n, k）线性分组码能纠正t个错误并能发现l（l > t）个错误的充分必要条件是

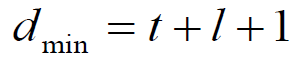
image.png

  • 译码过程
  • 译码器根据编码规则和信道特性，对所接收到的码字进行判决
  • 设发送的码字为C,接收到的码字R=C+e,其中e为错误图样，它指示码字中错误码元的位置。当没有错误时，e为全零矢量。
  • 定义接收码字R的伴随式（或校验子）为

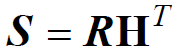
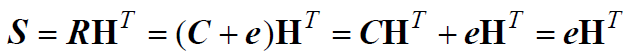
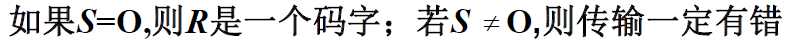
image.png
image.png
image.png

  • 可见伴随式仅与错误图样有关，与发送的具体码字无关
  • (n , k)线性码对接收字的译步骤如下：

image.png

3.2.2 分组码举例

  • 汉明码

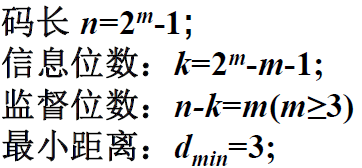
image.png
image.png

  • 循环码

(n , k)线性分组码的每个字经过任意循环移位后仍然是一个分组码的字
循环编步骤为：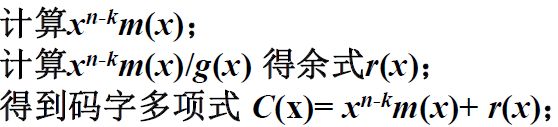
image.png
循环码特别适合误检测，用于误差检测的循环码称作循环冗余校验码 CRC( Cyclic Redundancy Check）

  • 例题

image.png

3.2.2 分组码移动通信应用

  • 在CDMA蜂窝移动通信的系统中，前向链路和反向链路在信道中消息是以帧的形式来传送的

image.png
这是一个（n, k）=(172+12,172)=(184,172)分组码
其生成多项式为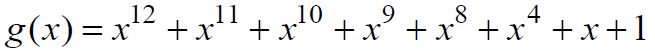
image.png

  • 在GSM 系统中话音信息、控制和同步在传输过程中都使用了 CRC 码

image.png
对重要的Ia类两重信道编码

3.3 卷积码

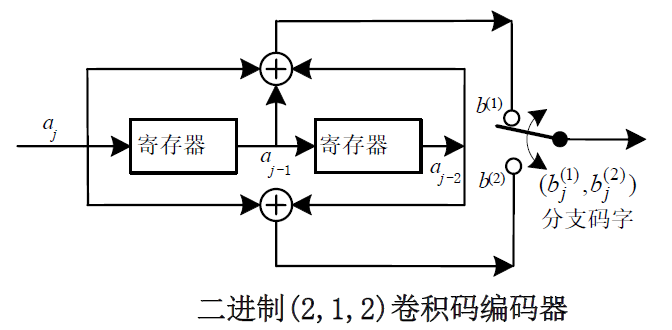
3.3.1 卷积码编码器

  • 卷积码编码器对输入的数据流每次1比特或k比特进行编码
  • 输出分支码字的每个码元不仅和此时刻输入的k个信息有关，也和前m个连续时刻输入信息元有关
  • 卷积码表示为（n,k,m）
  • 编码率【移动通信】抗衰落技术_信道编码 - 图22
  • 例如：

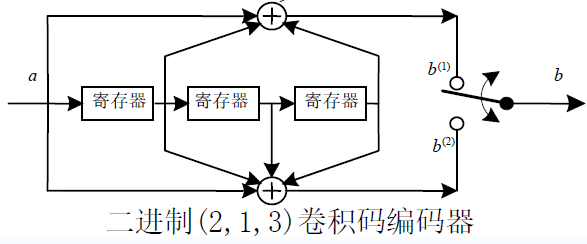
image.png

  • 编码器只有一个输入序列a，它经过两条不同的路径到达输出端，对应两个长度K=4的响应序列,

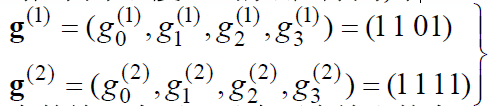
image.png

  • 对任意的输入序列a, 对应两个输出的序列分别是a与g(1)、g(2)的离散卷积

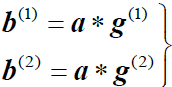
image.png

  • 还可以用生成多项式来进行表述，它定义为沖激响应的单位时延变换
  • 对应第i条路径的生成多项式定义为

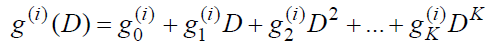
image.png

  • 对应前面的(2,1,3)编码器

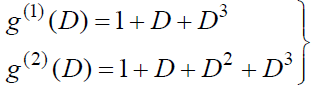
image.png

  • 信息序列可以表示为信息多项式

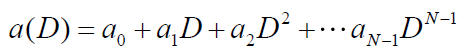
image.png

  • 相应的第i条路径输出序列多项式则等于

image.png

3.3.2 状态图

  • 编码过程可以用状态图来表示
  • 它描述了编码器每输入一个信息元时，编码器各可能状态以及伴随状态的转移所产生的分支码字

image.png

  • 上图用状态图表示

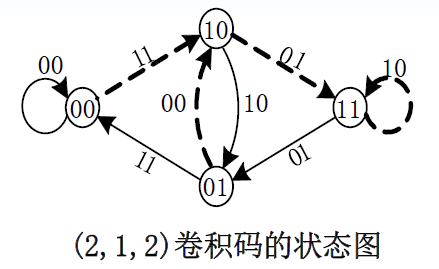
image.png

  • 图中小圆内的数字表示状态
  • 连接小圆的箭头表示状态转移的方向
  • 用连线的格式表示状态转移条件 （输入的信息比特）
  • 若输入信息比特为1，连线为虚连线
  • 若输入信息比特为0，连线为实连线

  • 连线旁的两位数字表示相应输出分支码字

    3.3.3 网格图

    网格图实际上是时间轴上展开编码器在各时刻的状态图
    设输入序列为10100，则输出变化路径如图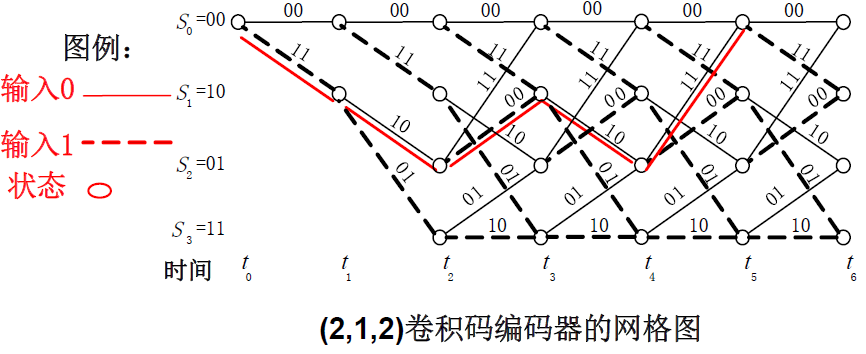
    image.png
    输出序列为11 10 00 10 11
    网格图中的首尾相连线构成了一条路径，对应着某个输入序列的编码输出序
    为了使结束后器回到初始状态，在信息比特后加m=2个0比特（拖尾比特）

    3.3.4 维特比译码的基本原理

  • 思想：维特比译码是基于最大似然法则的最重要的卷积码译码方法

  • 实现：
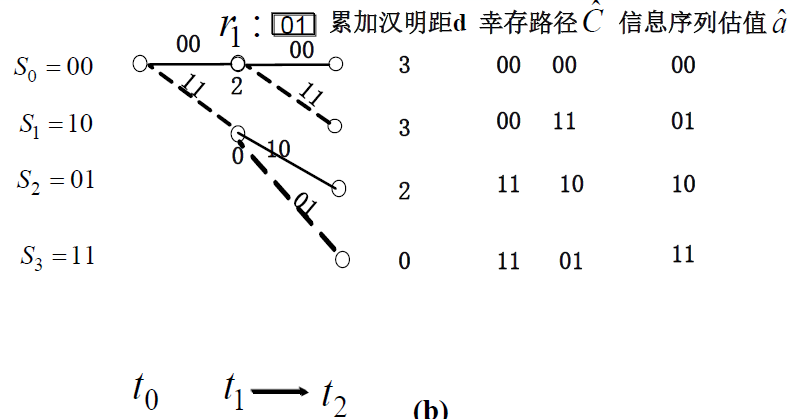
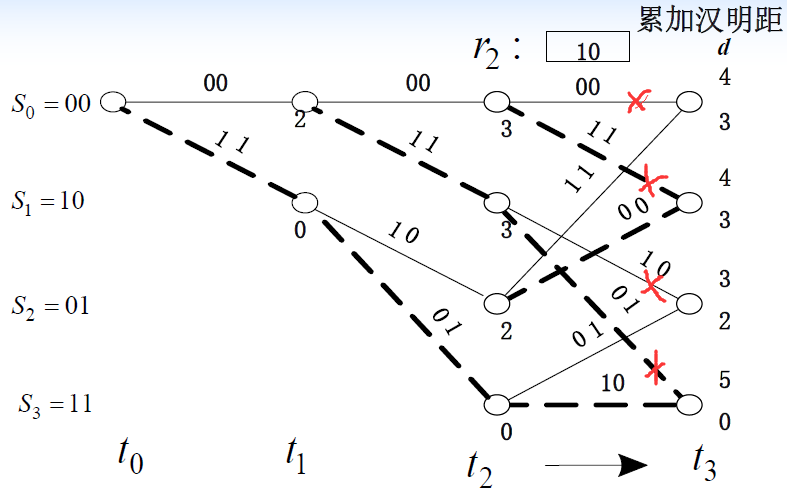
    • 采用逐步比较，就是把接收序列的第 j个分支码字和网格图上相应的两个时刻 tj和tj＋1之间的各支路作比较，计算和记录它们的汉明距，同时把分别累加到 tj时刻之前的各支路累加的汉明距上
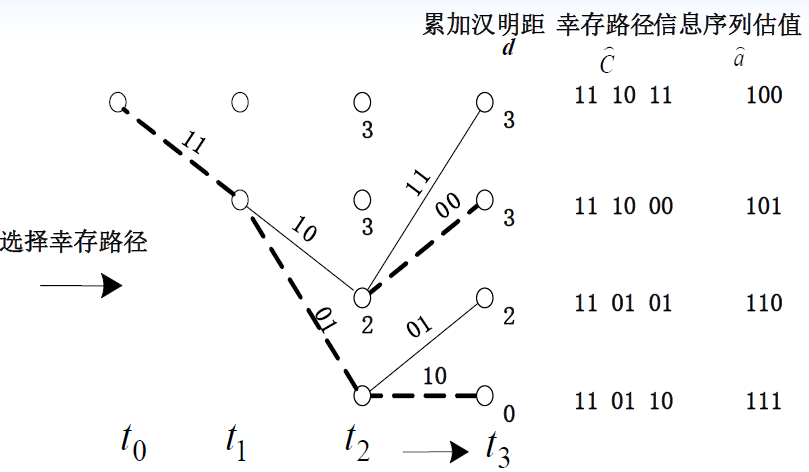
    • 比较累加结果并进行选择，保留汉明距离最小的一条路径，其余的被删除。所以 tj＋1时刻进入每个节点的路径只有一条，且均为幸存支路
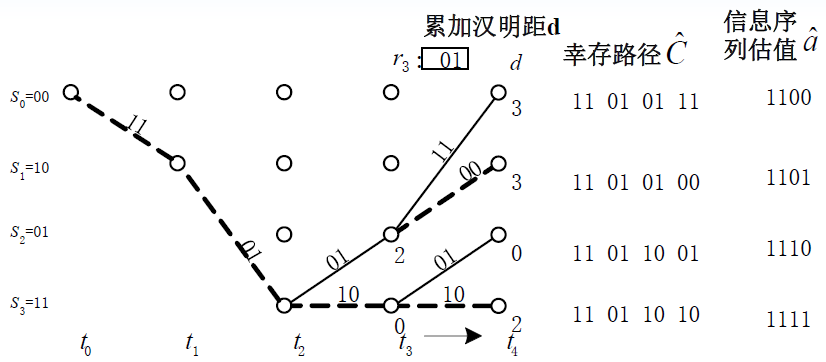
    • 这一过程直到接收序列的分支码字全部处理完毕，具有最小汉明距的路径判决为发送序列
  • 例题

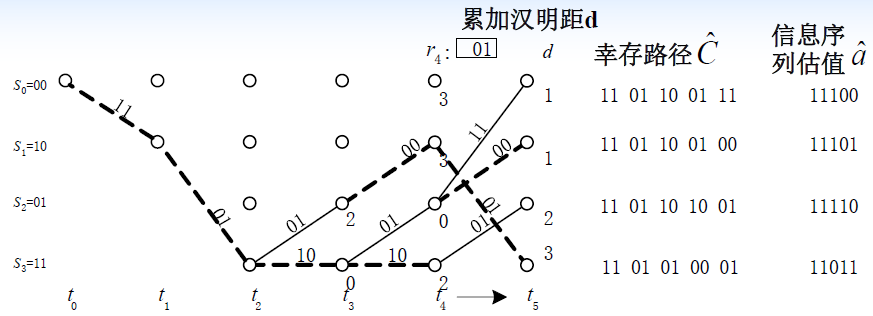
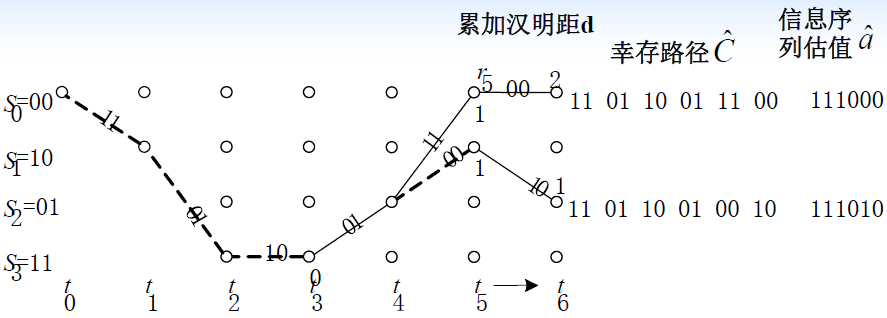
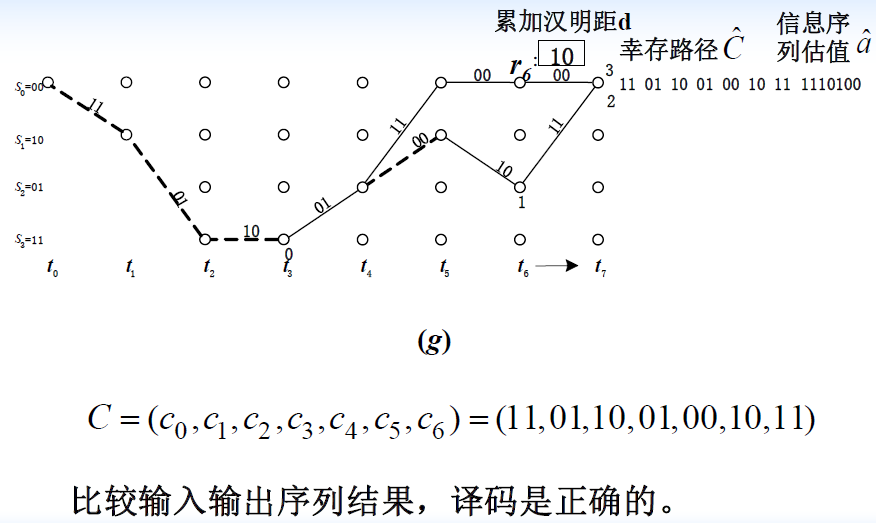
image.pngimage.pngimage.png
image.pngimage.pngimage.png
image.pngimage.pngimage.png

3.3.5 卷积码的自由距离

根据分组码理论，码字最多可以纠正错误的个数t由最小距离dmin确定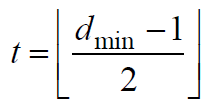
image.png
在卷积码中， dmin用被称为自由最小距离df取代
当且仅当df≥2t时，卷积码才能纠t个误码
对给定n, k, m,编码器可以有不同的结构（连接方式），但卷积码应被设计成具有最大的自由距离的“好”的卷积码

为了简单起见 , 表中把多项式系数矢量（称连接矢量）用 8进制表示
例如 r=1/2, =1/2,K=9 ,连接矢量为(101110001)→(561), （111101011)→(753)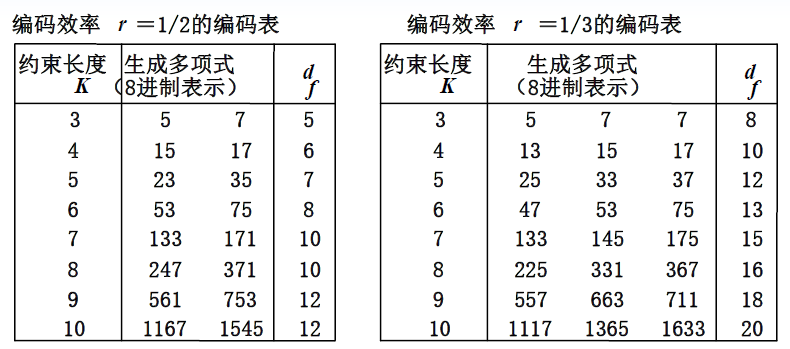
image.png

3.3.6 在蜂窝移动通信系统的应用

image.png

3.4 Turbo码

3.4.1 概述

  • 并行级联卷积码
  • 巧妙将卷积码和随机交织器（时间分集）结合，实现了随机编码的思想
  • 采用软输出迭代译码来逼近最大似然译码

  • 达到了近Shannon限的性能

    3.4.2 编码器

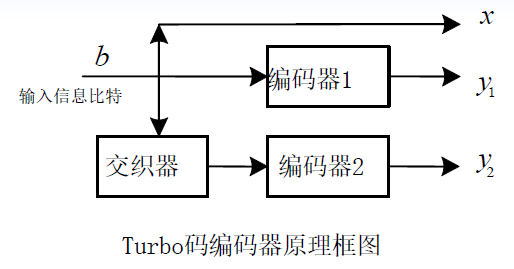
    image.png

  • 输入的数据比特流直接输入到编码器1

  • 同时也把这数据流经过交织器重新排列次序后输入到编码2
  • 由这两组编码器产生的奇偶校验比特，连同输入信息比特组成Turbo码编码器的输出
  • 编码率为【移动通信】抗衰落技术_信道编码 - 图46

例查表得到(2,1,4)NSC卷积码的生成矩阵是（37，21），找出相应的RSC码

  • 将八进制表示的生成函数矩阵表示成二进制系数

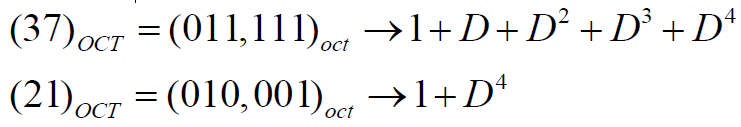
image.png

  • 生成函数矩阵为

image.png

  • 为了系统化，可对矩阵实施运算以造就一个单位阵，用 G(D)的第一列归一化

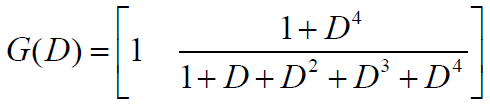
image.png

  • 实现了由NSC编码器到RSC编码器的转换
  • NSC码和RSC码各自的电路如图

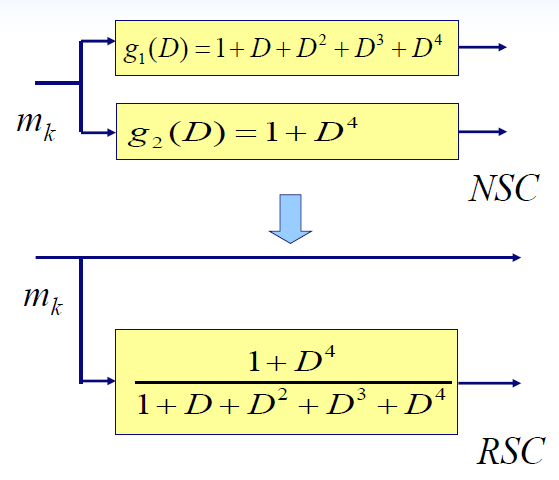
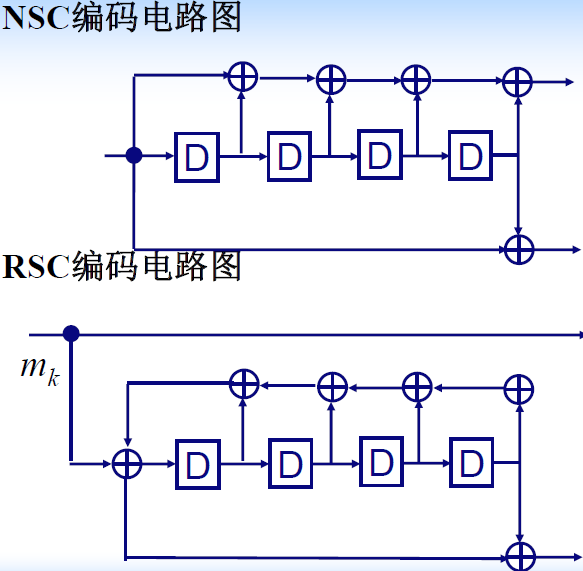
image.pngimage.png

  • 递归卷积码编码器RSC

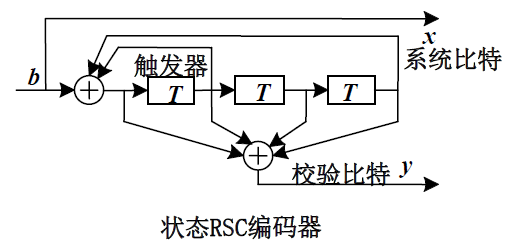
image.png

  • 传输函数可以表示为

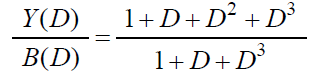
image.png

  • 表示了信息序列和校验序列的约束关系

image.png

  • 在时域信息比特和校验比特的关系为

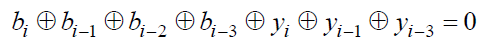
image.png

  • 由于RSC比一般的非递归卷积码有更大的自由距离，因此有更大的抗干扰能力，误比特率更低
  • 交织器：此处为伪随机交织器，在要发射的信息中加入了随机特性，作用类似与香农的随机码
  • 它使得两个编码器的输入互不相关，编码近似于独立
  • 由于译码需要交织后的信息比特位置信息，所以交织是伪随机的

    3.4.3 译码器

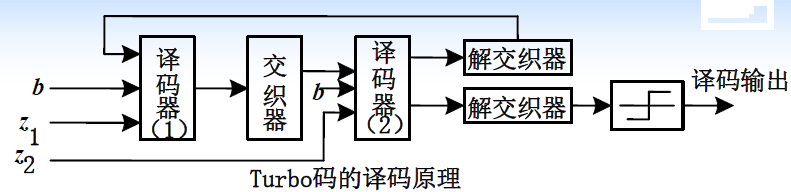
    image.png
    b为带噪声的系统比特，Z1、Z2是两个带噪声的校验比特
    Turbo码译码采用后验概率译码，两个译码器均采用BCJR算法

    3.4.4 应用

    image.png

4. 形象理解

image.png
交织编码
image.png
交织深度越大，交织编码处理时间越长，从而造成数据传输时延增大，是以时间为代价的编码方法