• 线性函数
  • f(x)=ax+b
  • f(x,y)=ax+by+c
  • f(x,y,z)=ax+by+cz+d

• 线性泛函

  • f(ax+by)=af(x)+bf(y)

• 非线性函数

  • 最简单的是多项式

求根过程

f(x), x∈[a,b]

• 根的存在性
• 根的隔离 将[a,b]分成若干小区间，每小区间至多一个根
• 根的精确化

二分法

前提：

• f(x)∈[a,b]连续 f(a)f(b)<0
• 加上精度限制

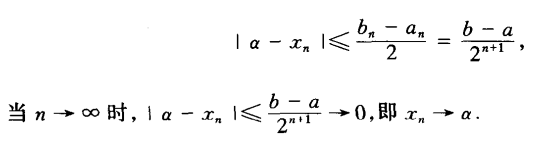
• 优点：计算简单，保证收敛性，函数性质要求低（连续即可）
• 缺点：收敛速度慢。不能求偶数重根，不能求复根和虚根

• 过程中函数值虽然计算，但未能利用上，仅用到了符号，造成浪费

  迭代法

• 构造递推关系式，即迭代格式，计算一个根的近似值序列，并希望该序列能收敛于方程的根

• 例如构造等价方程f(x)=0
• 为

• 迭代类型

收敛速度

• 收敛阶，描述迭代接近收敛时迭代误差下降的速度

• 效率指数