1. 椭圆轨道计算

1.1 开普勒第一定律

椭圆/质心
抛物线方程：
半长轴，短轴，焦距关系：
偏心率：
远地点长度：
近地点长度：
远地点高度：
近地点高度：
极坐标方程：
半焦弦：

1.2 开普勒第二定律

相同时间相同面积
开普勒常数：
卫星瞬时速度：
求远地点近地点速度，即把 带入
圆轨道恒定瞬时速度：，即将 带入

1.3 开普勒第三定律

周期的平方与轨道半长轴的立方成正比

• 例题

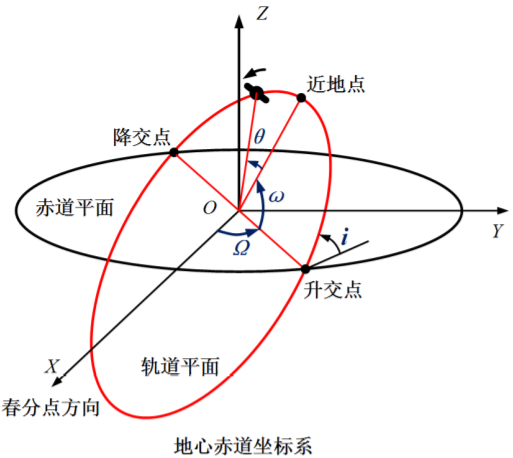
2. 轨道参数

2.1 轨道六要素

2.1.1 轨道形状

：半长轴
：偏心率

2.1.2 卫星位置

：平均近点角

2.1.3 轨道位置

：近地点幅角
：轨道倾角
：升交点赤经

• 例题

3. 确定卫星位置

确定卫星位置的最终目的是确定真近点角，即从地心出发，卫星位置与近地点形成的夹角
想要知道，需要通过高斯方程实现从偏近点角到的转换，即需要知道偏近点角
想要知道，需要通过求解开普勒方程，通过平均近点角求出偏近点角

卫星在时刻通过近地点，以平均角速度绕椭圆轨道外接圆移动
—-> 求出T


—-> 开普勒公式求出E
—-> 高斯方程求出θ

瞬时卫星到地心的距离r

其中开普勒公式中求解E采用Newton法

迭代方程

Newton迭代法

4. 卫星覆盖计算

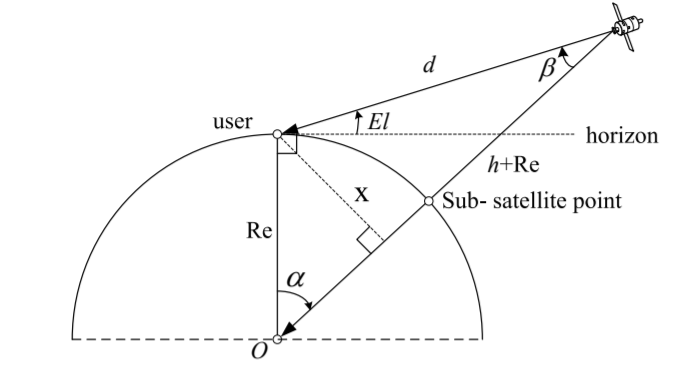
一般可知(地球半径),(近地点高度),(观察点对卫星仰角),求解其它数值
求解(卫星与观察点地心角)

(理应能用余弦定理推导出来,但太复杂)

求解(卫星到观察点距离)


求解A(卫星覆盖面积)

常利用经纬度计算地心角
**

• 例题

5. 轨道摄动

开普勒轨道为理想轨道

• 地球是理想的球体————————椭圆体,赤道宽于两极
• 卫星仅受地球引力场作用————-受其它行星引力场作用
• 卫星和地球都被视为点质量物体—存在非引力场作用,太阳光压,大气阻力

6. 轨道对通信性能的影响

6.1 多普勒频移

(注意和无线电定位中的公式不一样)
卫星通信是地面站发,卫星接收,不需要一来一返,测得的是卫星接收到的多普勒频移
而雷达是收到回波的多普勒频移,两倍距离

• 例题

6.2 日蚀

卫星进入太阳的地球阴影区,发生在春分和秋分前后
发生日蚀时太阳能板无法充能,通信效能下降

6.3 日凌中断

卫星运行在地球和太阳之间,发生在春分和秋分前后
太阳进入了地球站天线的波束范围,此时太阳噪声大,使得卫星信号完全中断

7. 卫星发射

• 第一宇宙速度(环绕速度)
• 第二宇宙速度(脱离速度)
• 第三宇宙速度(逃逸速度)

环绕速度和脱离速度随卫星高度不同而不同,轨道越高,地球对卫星引力越小,环绕速度和脱离速度越小

7.1 计算公式

椭圆轨道
圆形轨道
静止轨道卫星的发射至少需要两次加速

1. LEO近地点加速,进入GTO(转移轨道)
2. GTO远地点加速,进入GEO

即便是两次加速的过程,
因为从近地点到远地点移动的过程会经历减速

8. 四大发射中心

J/X/T/W SLC(Satellite Launch Center) 酒泉/西昌/太原/文昌 卫星发射中心