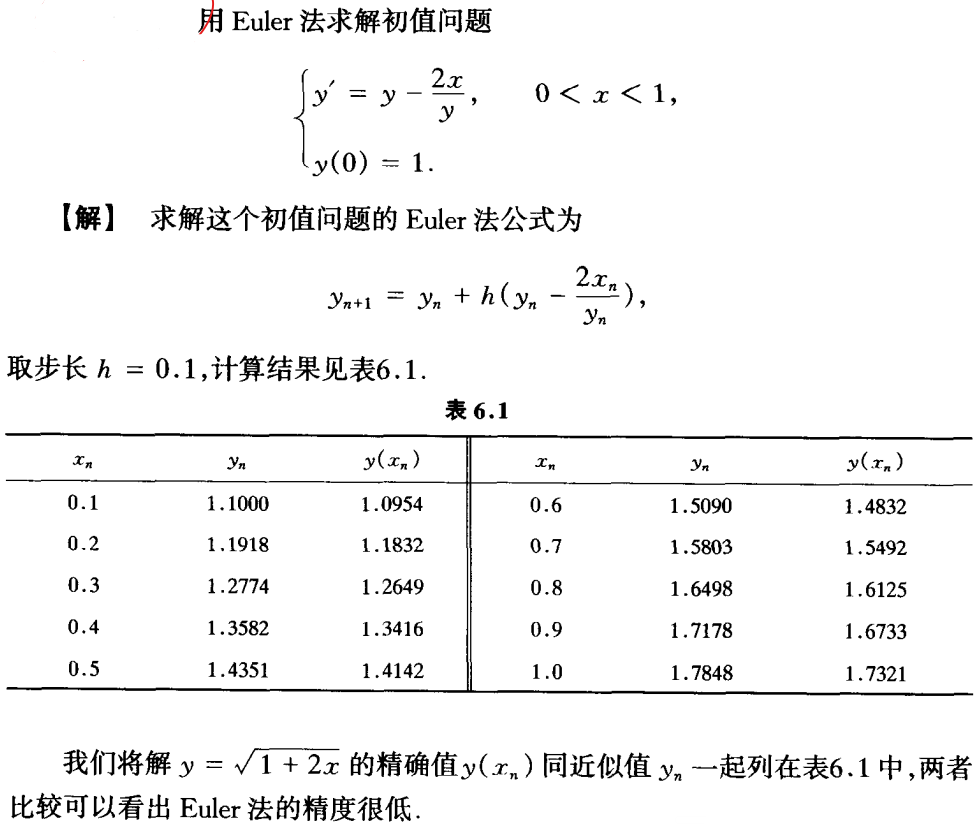
一阶常微分方程初值问题

• 求解y(x)的表达式
• y0用来求解常数

• 正常解法为，一阶齐次，分离变量

  显式Euler法

• N等分[a,b]

• 求y在的近似值

• 此即为显式Euler法

隐式Euler法

• 得到的是关于的方程

• 没有显式的直接迭代容易计算

  局部截断误差

• Euler法可以统称为单步法

• 单步法的一般形式

• 判断方法好坏，需要测量误差
• 定义局部截断误差

• 定义阶：若称该方法为P阶
• 因此由前面计算可得显式Euler法为一阶
• 如果真解为一次多项式，可得
• 此时求得的为精确解
• 例题

Euler两步法

Runge-Kutta法

• 在导出Euler法(1阶方法)时，只用到了Taylor展开式的前二项
• 如果想获得求解问题更高阶的方法，可以采用更多的项，如用r+ 1项，就可得到r阶Taylor级数法

• 局部截断误差为

• RK法的一般形式

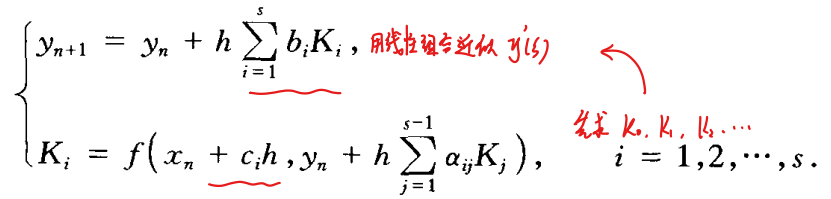
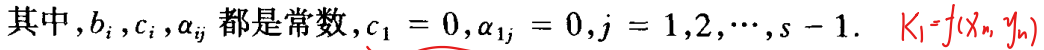
• K的表示式可见为显式单步法，一般每步需要计算s次f(x,y)的值，故称其为s级RK法

• s级RK方法的局部截断误差

• 常数可用待定系数法确定，确定的原则是将局部截断误差按Taylor级数展开，选取系数使它关于h的阶数尽可能高一些，即尽量使方法达到最高阶

  二级RK法

• 当s=2时

• 求局部截断误差

• 此时需要用到二元Taylor展开
• 将在点Taylor展开得

• 可得截断误差

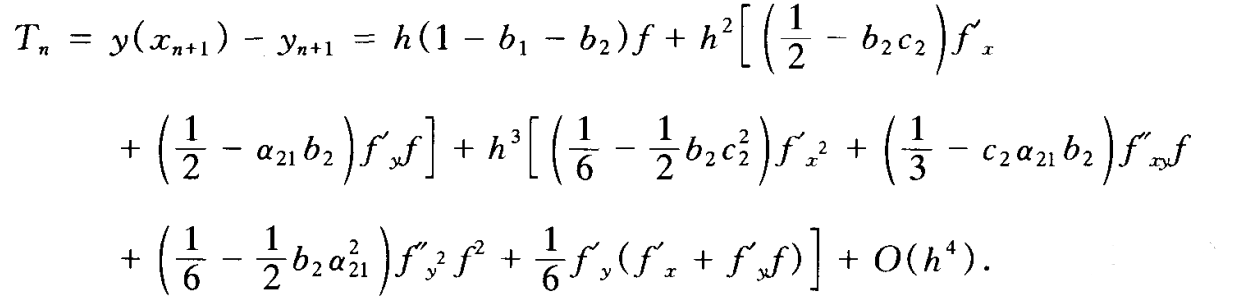
• 要使的阶数尽可能地高,应选取使上式右边和的系数为零,即满足方程

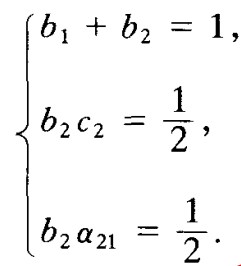
• 这是4个未知数的3个方程,有无穷多解。以为自由参数得

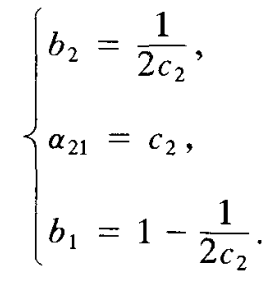
• 此时

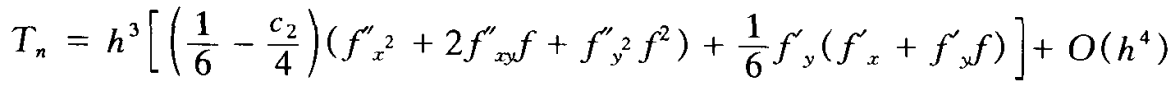
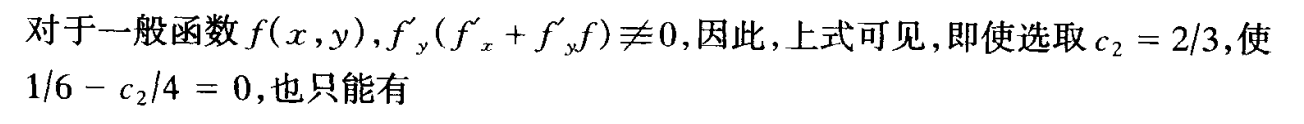
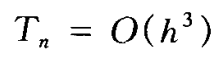
• 这说明二级RK法最高只能达到2阶
• 常用二级2阶RK法

（1）中点方法（）

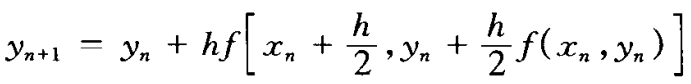
（2）Heun方法（）

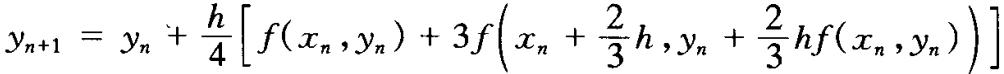
（3）改进的Euler方法（）

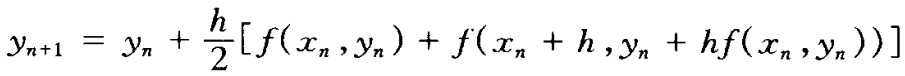
单步法的一般性理论

• 相容性：

若

• 即差分方程趋近于微分方程
• 满足相容，才能保证差分方程是有意义的
• 因此至少，至少是一阶的方法才能保证相容
  • 收敛性：

• 差分方程的解趋于微分方程的解
  • 稳定性：

• 如果y0不同导致解有很大的波动即不稳定

• 提供一个测试方程，判断求解方法的好坏
• 模型方程

• 考虑显式Euler法

  - 稳定需要满足

  - 此时![](https://cdn.nlark.com/yuque/__latex/67371a38d65fd972973ce60f838cdbed.svg#card=math&code=h%5Clambda&id=Cq1Mm)得到了绝对稳定区间

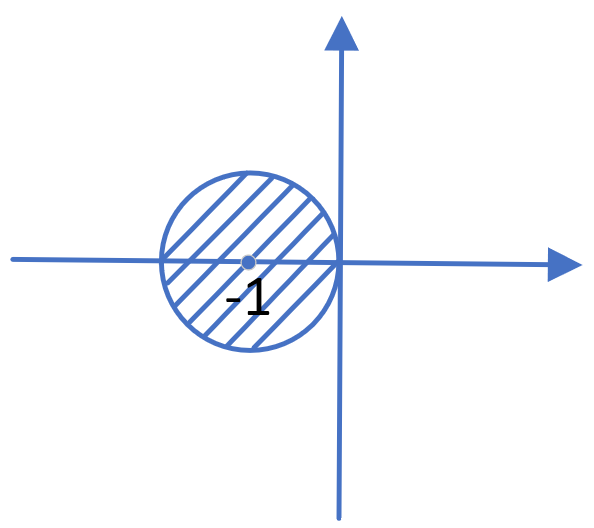
  - 决定了步长的取值方式

• 考虑隐式Euler法

  - 稳定需要满足

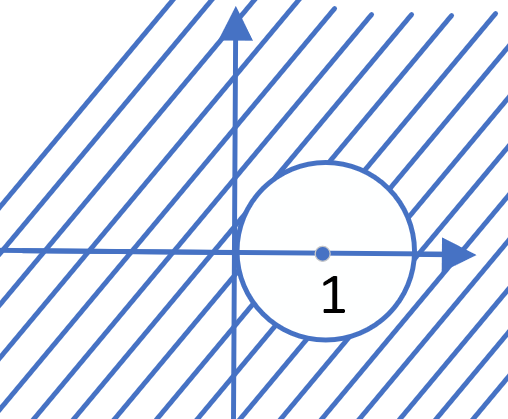
  - 分段计算

  - 由此可以注意到此时绝对稳定区间范围更大
  - 所以隐式Euler法h随便取都可稳定

• 例题

• 用显Euler法

• y(10)需要计算500步
  • 隐Euler法

• h可以随意取
• 为准确可以取0.5
• 此方法更好，但是计算复杂

  线性多步法

• 线性多步法的一般形式

• 特定方法中可以为0
• 该式实现的是步法，不同时为0
• 如果则该式为隐格式
• 类比Euler两步法

• 阶的概念：局部截断误差

• 为P阶，对y(x)是r次多项式时，方法是精确的，对r+1次，是不精确的，该方法是r阶的
• Euler法是1步1阶方法
  • 局部截断误差

• 其中C的计算

• 线性多步法是r阶的充分必要条件是定义的满足关系式

• 因此满足条件的线性多步法是1阶的，是相容的，相容的方法至少为1阶
• 由此可构造指定阶数的方法
• 得到一个关于的方程组
• 有p+1个，有p+2个，未知数一共有2p+3个
• 方程数为q+1
• 只有当2p+3=r+1时才有唯一解，由此得到结论：
• 方法能达到的最高阶数为步数的2倍，即
• 2p+2为最高阶，且仅有一个
• 稍低一点将有无穷解
  • 例题

多步法的一般性理论

• 测试方程

• 将上式记为
• 也称特征多项式、稳定多项式
• 设

• 收敛性
  • 定义：方法、公式满足根条件：
    • 的根的模均不大于1，模为1的根为单根
  • 定义：
    • 方法、公式如果收敛➡满足根条件
    • 方法、公式如果收敛➡相容（阶至少为1，C0=C1=0），或者
    • 均为正向推导
  • 定义：
    • 如果公式既满足根条件又相容⬅➡公式是收敛的
• 稳定性
  • 稳定多项式
  • 与的根有关

• 记
• 如果没有极限是1的解，谁接近1谁是
• 绝对稳定
  • 若对任意的均有

  - 则方法在![](https://cdn.nlark.com/yuque/__latex/ff9dac79adb404e3f441201f476b92df.svg#card=math&code=%5B%5Csigma%2C%5Cdelta%5D&id=PexBN)是绝对稳定的，即误差越算越小
  - ![](https://cdn.nlark.com/yuque/__latex/ff9dac79adb404e3f441201f476b92df.svg#card=math&code=%5B%5Csigma%2C%5Cdelta%5D&id=UrALz)为绝对稳定区间
  - 若![](https://cdn.nlark.com/yuque/__latex/ff9dac79adb404e3f441201f476b92df.svg#card=math&code=%5B%5Csigma%2C%5Cdelta%5D&id=EKTR3)包含（-∞,0）则成为A稳定

• 相对稳定
  • 若对任意的

  - 则称方法在![](https://cdn.nlark.com/yuque/__latex/76ec9b92b11ea1475095ec6a47fccd53.svg#card=math&code=%5B%5Calpha%2C%5Cbeta%5D&id=VrNMR)是相对稳定的（误差相对真解是小的）
  - ![](https://cdn.nlark.com/yuque/__latex/76ec9b92b11ea1475095ec6a47fccd53.svg#card=math&code=%5B%5Calpha%2C%5Cbeta%5D&id=xozkG)为相对稳定区间

• 例题