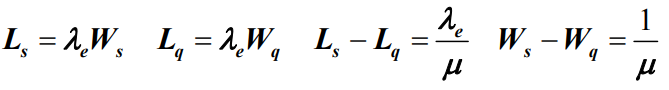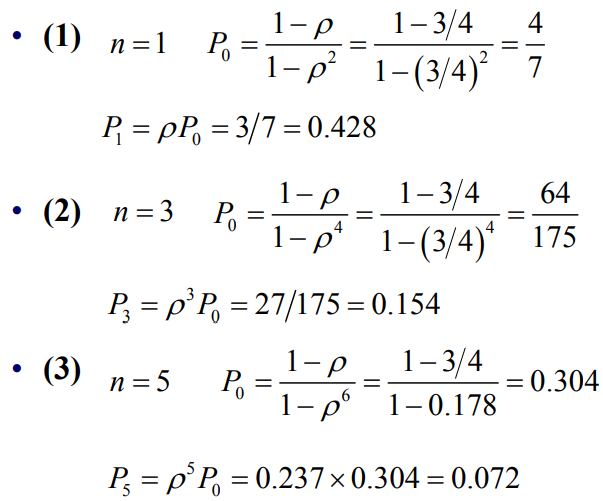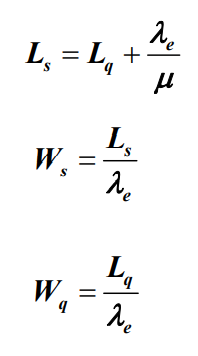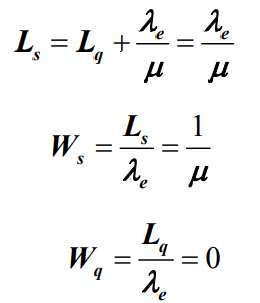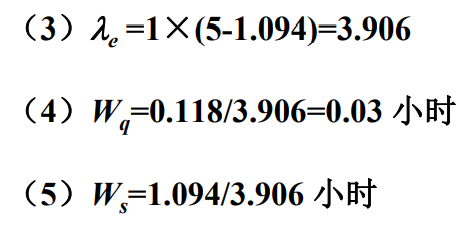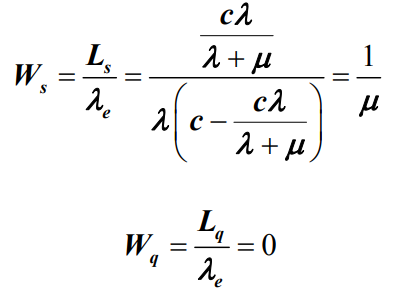5.3 排队论基础理论
5.3.1 排队系统的组成
- 排队系统的组成方式有很多,但决定排队系统的进程的主要因素三部分组成:输入过程、排队规则和服务机构。它们之间的关系如下图所示
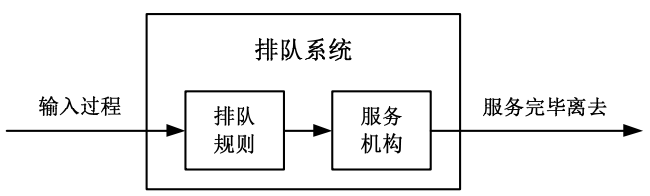
- 1. 输入过程
- 输入过程是用来描述顾客来源以及顾客到达排队系统的规律。输入过程包含三个方面的内容:
- 顾客总体数
- 指的是顾客的来源(简称顾客源)数量。对于不同的排队系统,顾客源既可以是有限的,也可以是无限的。
- 顾客到达方式
- 用来描述顾客是按照什么样的数量方式到达排队系统的。顾客到达方式可以是单个到达,也可以是成批到达;可能是离散的,也可能是连续的;可以是相互独立的,也可以是相互关联的。
- 顾客到达时间间隔分布
- 指的是相继到达系统的顾客,其到达时间间隔服从什么样的概率分布。
- 顾客相继到达的时间间隔可以是确定的,也可以是随机的。
- 如果描述顾客到达的时间间隔分布和所含参数都与起始时间无关,则为平稳输入过程,否则为非平稳输入过程。
- 2. 排队规则
- 排队规则包括排队系统类型和服务规则两方面内容:
- 排队系统类型
- 排队系统类型主要和排队系统允许的排队队长n(或称为截止队长)以及服务窗口数m有关。
- 一般来说,排队系统类型有以下三种:
- 当m=n<∞时, 该系统被称为损失制系统(也称为即时拒绝系统、立接制系统)。此时顾客到达排队系统,如果所有窗口都在工作(或被占满),顾客当即离去,不存在排队等候的情况。如普通市内电话的呼叫就是这种情况。
- 当m<n<∞时,该系统被称为等待制系统(也称为延时拒绝系统、缓接制系统)。此时存在排队等候的情况,排队系统允许一定数量的到达顾客在系统缓存中等待。一旦系统内的顾客总数达到截止队长时,新来的顾客就因被拒绝而离去。如分组交换以及带有缓存的数据通信就是这种情况。
- 当m<n=∞时,该系统被称为非拒绝系统(也称为非截止系统)。这种情况其实就是延时拒绝系统的一种特例。此时系统存在排队等候的情况,并且系统允许的排队队长无限(一般认为顾客数量是无限的)。新来的顾客在所有窗口都被占满时不会离去,而是永远的在系统缓存中等待直到接收服务为止。虽然允许的排队队长在实际中不可能是无限的,但是当系统缓存容量足够大时,就可以认为允许的排队队长是无限的。比如网络存储系统就是这种情况。
- 在上面分析的三种情况中,第一种和第二种情况经常被简称为拒绝系统,三种情况的关系如下所示。
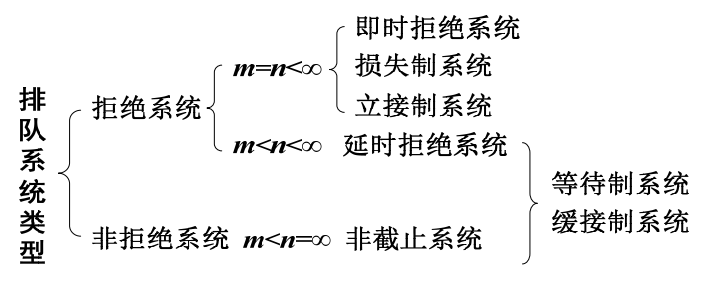
- 服务规则
- 服务规则是指排队系统中顾客等待服务的顺序,它不仅与顾客达到的规律有关,也与排队系统的类型有关。服务规则主要有以下几种:
- 先到先服务:系统按照顾客到达的先后顺序为顾客服务。这种情况是最一般的、常见的服务规则。若无其它说明,这种情况是默认的服务规则。
- 后到先服务:系统按照顾客到达的顺序,后到的顾客先接受服务。这种情况常见于计算机堆栈系统。
- 优先制服务:系统按照顾客被赋予的优先级对顾客服务。顾客的优先级越高,越被优先服务。其本质是一种顾客插队的服务形式。这种优先制服务又可以分为强拆型优先制服务和非强拆型优先制服务。
- 强拆型优先制服务是指,当优先级较高的顾客到达系统时,无论正在接受服务的顾客(优先级较低)是否接受服务完毕,都必须立即终止服务,系统优先为级别较高顾客服务。顾客插队遇到相同级别的顾客时,一般情况默认正在接受服务顾客优先级高。
- 非强拆型优先制服务是指,当优先级较高的顾客到达系统时进行插队,必须等待正在接受服务的顾客服务完毕后才会得到服务。这种情况常见于集群通信系统。
- 3. 服务机构
- 服务规则是指排队系统中顾客等待服务的顺序,它不仅与顾客达到的规律有关,也与排队系统的类型有关。服务规则主要有以下几种:
- 服务机构包括三个方面的内容:
- 服务窗口(或服务员)数量:
- 服务窗口数量的划分非常简单。当m=1时,称为单窗口排队系统,当m>1时, 称为多窗口排队系统。
- 服务方式:指的是系统如何排列服务窗口为顾客提供服务。
- 串列式服务就是将m个服务窗口串列起来,这些窗口提供的服务内容可以相同也可以不同,但每个顾客必须依次经过所有m个服务窗口才能完成全部服务,并且在任意一个时刻只能有一个顾客接受其中某个窗口的单项服务。
- 并列式服务就是将m个服务窗口并列起来,通常认为这些窗口提供的服务内容相同。每个顾客只需经过任意一个窗口就可以完成全部服务。在任意-一个时刻也只能有一个顾客接受其中某个窗口的单项服务。
- 混合式服务就是综合了串列式服务和并列式服务的窗口排列方式。这种服务方式是最常见的。
- 排队方式:是指如何客户如何排列接受服务。排队方式分为分别排队和混合排队。
- 混合排队是指顾客排成一个队列。
- 分别排队是指顾客排成m个队列接受m个服务窗口的服务。
- 服务窗口(或服务员)数量:
- 根据不同的服务方式和排队方式组合,排队模型结构可以千变万化。下图列出了常见的五种情况,即:
- 混合排队串列式服务、分别排队并列式服务、混合排队并列式服务、混合排队串列式服务、混合排队混合式服务。
5.3.2 排队模型的符号表示
- 排队论模型最早的表示方法,是英国数学家肯德尔在1953年提出来一种分类方法。
- 他按照系统的三个最主要的、影响最大的特征要素进行分类,即:顾客相继到达的时间间隔分布、服务时间的分布以及并列的服务窗口数量。
- 按照这三个特征要素分类的排队系统用符号表示为X/Y/Z,.上述表述方法也称为肯德尔记号。 后来,将这种符号扩充为下面的形式:

- 各个符号的含义如下:
- X:描述顾客相继到达的时间分布,用分布描述符号表示。
- Y:描述服务时间分布,用分布描述符号表示。
- Z:描述并列的服务窗口数量,常用符号m表示。
- A:描述系统的排队截止队长,也就是系统的最大缓存容量,常用符号n表示;如果省略,即表示截止队长n=∞。
- B:描述顾客源的顾客数量,常用符号c表示;如果省略,即表示顾客数量c=∞。
- C:描述服务规则用服务规则符号表示,如果省略,即表示先到先服务。
- 这里需要特别注意的是,系统的排队队长包含服务窗口数量,因此在排队模型的符号表示方法中有如下关系:
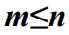
- 分布描述符号用来描述顾客相继到达时间分布(X)和服务时间分布(Y) :
- M:表示泊松流(最简单流)或负指数分布,随机排队模型称为马尔科夫(Markov) 型,取其字头为M;
- D:表示确定性(Deterministic) 分布;
:表示k阶爱尔兰(Erlang) 分布;
- GI:表示一般相互独立(General Independent)的随机分布;
- G:表示般(General) 随机分布。
- 服务规则符号(C) :各种服务规则可以是如下的描述符号:
- FCFS:先到先服务;
- LCFS:后到先服务;
- FIRS:先来随机服务。
- 其中,后面三个符号A/B/C是可选项,可以省略。如果省略后三项时,即指
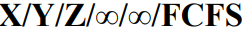 的情况
的情况 例如:
排队系统有五个基本参数决定了排队系统的主要性能指标,它们分别是:
- 顾客数量
- 服务窗口数量
- 顾客到达速率
- 服务速率
- 服务强度
- 顾客数量
- 由两个部分组成,包括正在排队等待的顾客数量、正在接受服务的顾客数量。它是一个离散型随机变量,用符号k(20)表示。
- 顾客数量
- 服务窗口数量
- 也称为服务员数量,它指的是系统可同时向顾客提供服务的服务设施数量。它描述了排队系统的资源量,一般来说,它是一个常数,用符号m(≥1)表示。当m=1时,称为单窗口排队系统,当m>1时,称为多窗口排队系统。
- 服务窗口数量
- 顾客到达速率
- 简称顾客到达率,也称为系统到达率。它可以是一个连续型随机变量,也可以是常数,用符号 λ (>0)表示。
- 顾客到达速率 λ 的定义是和顾客源的定义有关系的。
- 当排队系统的顾客源是无限的时候,定义为单位时间内到达系统的平均顾客数,单位:个/单位时间
- 当排队系统的顾客源是有限的时候,定义为每个顾客的平均到达率,单位:(个/单位时间)/个
- λ 表征了顾客到达系统的快慢程度,也表征了顾客对系统所需服务的要求
- λ 越大,系统的负载就越大;
- λ 越小,系统的负载就越小。
- 顾客到达速率的倒数是平均到达时间间隔
,即有:
- 顾客到达速率
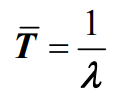
- 服务速率:分为窗口服务速率和系统服务速率。
- 窗口服务速率指的是单位时间内一个服务窗口(或服务员)进行服务时顾客离开系统的平均数。它可以是一个连续型随机变量,也可以是常数,用符号 μ 表示。
- 系统服务速率也称为系统离开率或顾客离开速率,它是一个数学期望值。
- 对于单窗口排队系统,系统服务速率等于窗口服务速率 μ
- 对于多窗口排队系统,假设每个服务窗口的窗口服务速率相同,当系统内顾客数量k小于服务窗口数量m时,系统服务速率为kμ ;系统内顾客数量k大于等于服务窗口数量m时,系统服务速率为mμ。
- 服务速率:分为窗口服务速率和系统服务速率。
- 服务强度
- 系统到达率是从顾客的角度来定义的参数,它反映了顾客希望系统能够提供的服务能力。
- 系统离开率则是从系统的角度而定义的参数,它反映了系统实际能够提供的服务能力。
- 系统的“实际”往往制约着顾客的“希望”
- 当系统到达率大于等于系统离开率,系统将变得不稳定(或处于临界状态)。此时,系统内的顾客会越来越多,排队等待的时间也会越来越长,并最终导致系统无法正常工作。
- 而如果系统到达率小于系统离开率,系统就是稳定的。此时,总能保证顾客在有限时间内接受服务。为此,定义服务强度p (或稳定性参数)来检验系统是否稳定:
- 服务强度
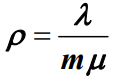
- 队长指标
- 排队队长简称队长,是一个离散型随机变量,它指的是系统中顾客数量,用符号 k 来表示
- 排队队长包括两个部分:在队列中等待服务的顾客数量和在服务窗口接受服务的顾客数量
- 队长的数学期望值称为平均队长,用符号
表示
- 等待服务的顾客数则被称为等待队长,其数学期望值称为平均等待队长,用符号
表示
- 若符号用
表示平均窗口占用数量,那么就有:
- 队长指标
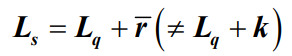
- 对于有限状态生灭过程有:
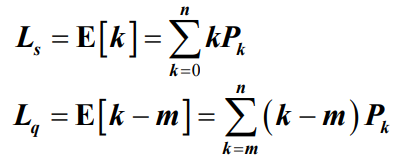
- 对于无限状态生灭过程有:
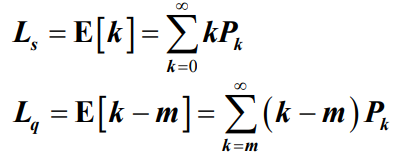
- 时间指标
- 等待时间指的是,从顾客进入排队系统的时刻算起到它开始接受服务时刻为止的这段时间,用符号
表示
- 等待时间是一个连续型随机变量,其数学期望值称为平均等待时间,用符号
表示,即有
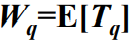
- 服务时间指的是,从顾客开始接受服务的时刻算起到它离开系统时刻为止的这段时间。服务时间是一个连续型随机变量,其数学期望值称为平均服务时间,用符号
表示
- 由前面分析可知,生灭过程的服务时间分布为指数分布,即服务时间间隔分布的概率密度
为:
- 等待时间指的是,从顾客进入排队系统的时刻算起到它开始接受服务时刻为止的这段时间,用符号
- 时间指标
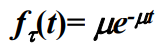
- 因此,完成服务的平均时间就是平均服务速率的倒数:
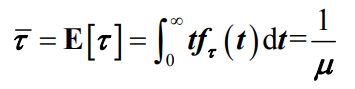
- 逗留时间指的是,从顾客进入排队系统的时刻算起直到它接受完服务离开系统的时刻为止的这段时间,用符号
表示。逗留时间也是一个连续型随机变量,其数学期望值称为平均逗留时间(或系统时间)用符号
表示,即有
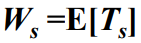
- 显然,平均逗留时间
、平均等待时间
。和平均服务时间
有如下关系:
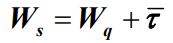
在假定到达与服务是彼此独立的条件下,平均逗留时间
与平均等待时间
是相互独立的
初始概率也称空闲概率,指的是系统内无顾客情况的概率,用符号
表示。它对应于系统状态是k=0的状态概率。
- 初始概率
反映了系统的闲与忙。如果
过大,则说明系统的利用率不高,经常处于空闲状态。反之,则说明系统利用率很高,经常处于工作状态。
- 排队论中也常使用系统效率这一概念,它指的是系统处于非空闲状态时的概率。系统效率越高,说明服务资源的利用率越高,用符号 η 表示
- 初始概率
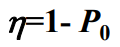
- 拒绝概率也称为阻塞概率、损失概率,指的是拒绝式系统内顾客已满系统无法再为新到的顾客提供服务时的稳态概率,用符号
表示
- Little定理(亦称李特定理)系统在稳定状态下,时间指标和队长指标有如下关系
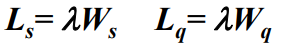
- Little定理推论:
- 对于无限状态生灭过程有:
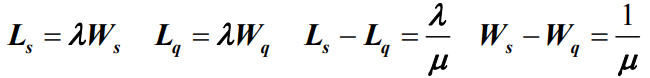
- 对于有限状态生灭过程有:
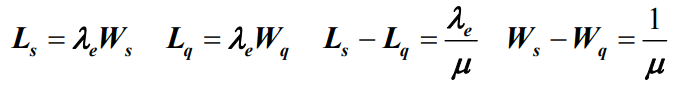
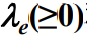 称为顾客有效到达率,或系统有效到达率,简称有效到达率
称为顾客有效到达率,或系统有效到达率,简称有效到达率和
一样,都是用来描述顾客实际进入系统的平均速率,因此有
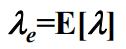
- 有限状态生灭过程只存在于三种情况:一是顾客源有限,二是截止队长有限,三是两者都有限
- 第三种情况可以看成是前两种情况的特例,即当顾客源数量小于等于截止队长时,第三种情况等同于第一种情况,而当顾客源数量大截止队长时,第三种情况等同于第二种情况。
- 下面分别考虑前两种情况
- 情况一:系统顾客源数量有限且为c
- 由于顾客源数量有限,λ 表示为每个顾客的平均达到率,顾客总数 c,已经进入系统的顾客数是 k,则系统的有效到达率是:
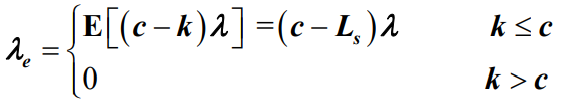
- 根据公式可知,随着用户不断进入系统,系统有效到达率
不断减小
- 当用户全部进入系统时,此时系统有效到达率为零。
- 情况二:系统截止队长有限且为n
- 对于顾客源数量是无限情况是,λ 表示为所有顾客的平均达到率。由于系统设置了截止队长n,因此当进入排队系统的顾客数量大于等于系统截止队长n时,新来的顾客将被拒绝进入系统。此时每个顾客到达的速率将变为0,而不再是 λ ,即系统有效到达率为
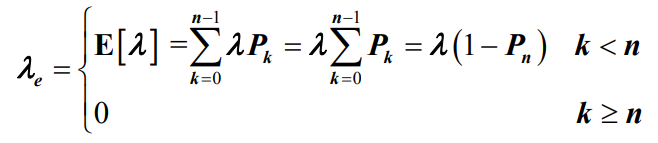
- 其中
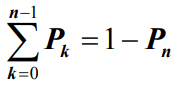
- 再次观察两个公式可以知道,尽管采用了不同的参数 λ 和
,但是这两个公式的含义其实质是一样的。这是由于对于无限状态生灭过程系统没有截止队长限制,因此,对于无限状态生灭过程有
。
- 对于无限状态生灭过程有:
- 再次观察两个公式可以知道,尽管采用了不同的参数 λ 和
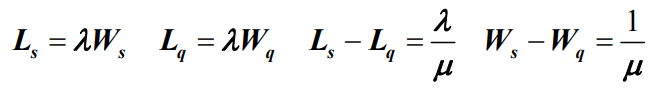
- 对于有限状态生灭过程有:
5.4 马尔可夫排队模型
5.4.1 M/M/1排队模型
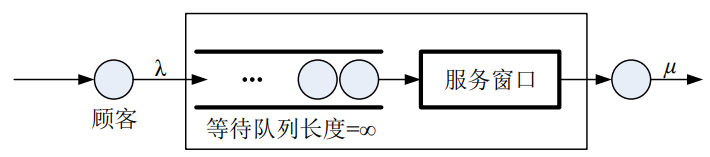
- M/M/1排队模型是最简单的单窗口非拒绝系统。它由一个队列和一个服务窗口组成,客户源数量无限,截止队长无限。其系统结构如下图所示。
- M/M/1排队模型满足参数为 λ 的泊松流输入条件,顾客的服务时间服从参数为 μ 的负指数分布。因此,该模型的顾客到达速率和窗口服务速率分别为
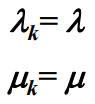
- 其状态转移图如下所示

- 根据状态转移图可知,M/M/1排队模型是一个无限状态生灭过程。那么根据公式
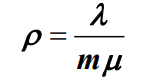 ,M/M/1排队模型的服务强度 ρ 为:
,M/M/1排队模型的服务强度 ρ 为:
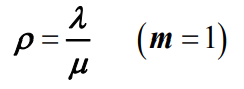
- 根据公式
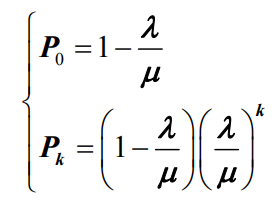 ,系统的初始状态概率 P0 和稳态概率 Pk 分别为
,系统的初始状态概率 P0 和稳态概率 Pk 分别为
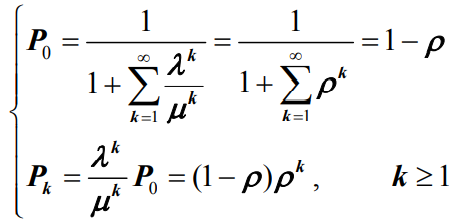
- 系统中有超过n个客户的概率为
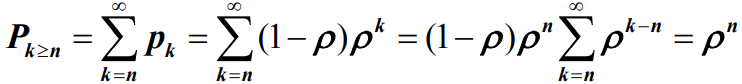
- 其中
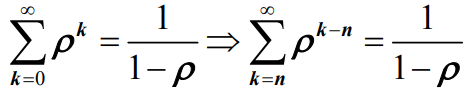
- 因此有
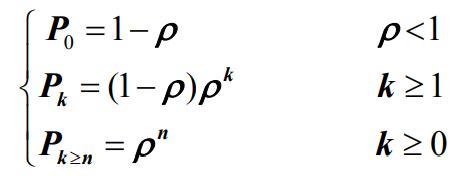
- 例题:

- 关于 ρ 的几点说明:

- M/M/1排队系统的主要性能指标
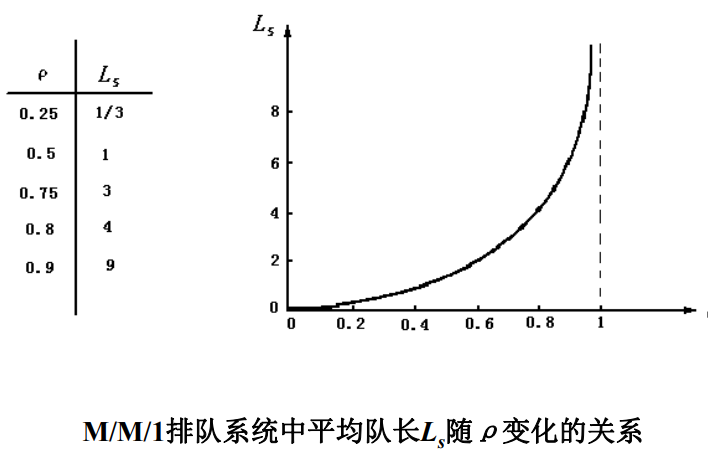
- 平均队长
:系统中平均顾客数
- 平均队长
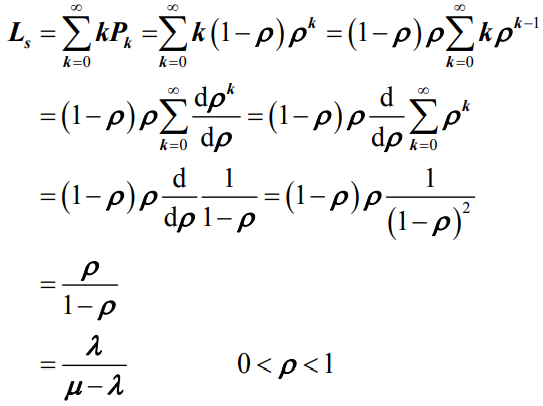
- 平均等待队长
:系统中正在排队等待的平均顾客数
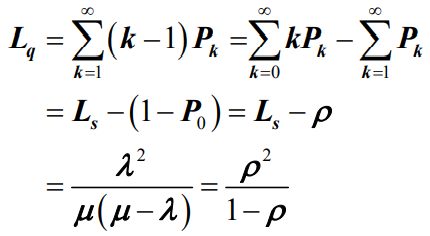
- 平均占用窗口数
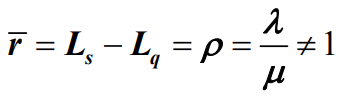
- 顾客平均等待时间 Wq
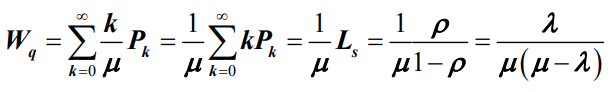
- 平均逗留时间 Ws
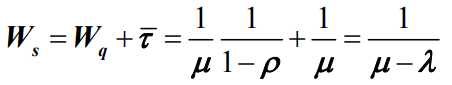
- 系统效率 η
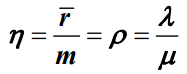

- 例题



- 在M/M/1排队模型中,逗留时间Ts(不是平均逗留时间WS)和等待时间Tq (不是平均等待时间Wq)也是经常用到的随机变量。
- 定理:对于M/M/1排队模型,顾客在系统中逗留时间 Ts 的分布函数为
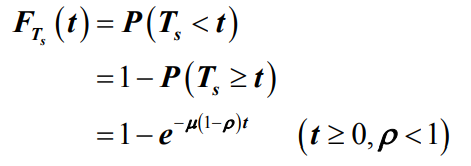
- 证明

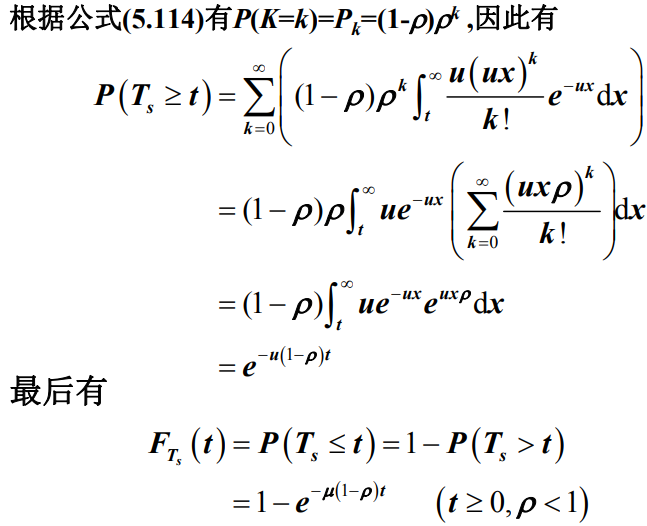
- 实际上,对逗留时间 Ts 的分布函数求偏导数就可以求出其概率密度函数
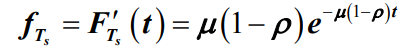
- 那么平均逗留时间Ws就是:
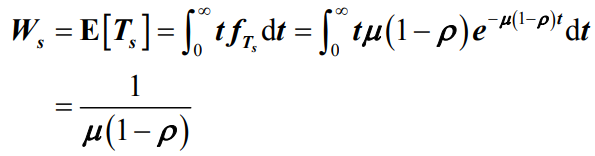
- 下面再来分析等待时间Tq
- 定理:对于M/M/1排队模型,顾客在系统中等待时间Tq的分布函数为
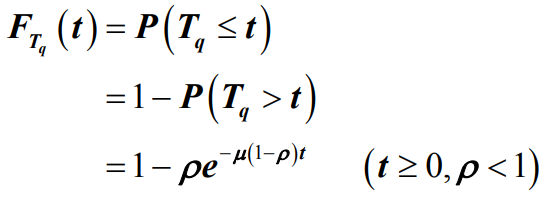
- 证明



- 如果对等待时间 Tq 的分布函数求偏导数也可以求出其概率密度函数
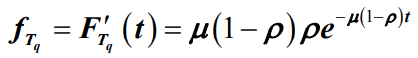
- 那么平均等待时间Wq分别为:
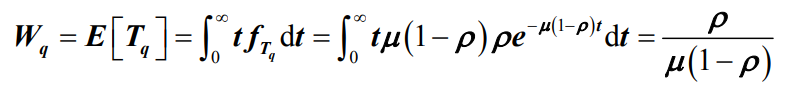
- 例题
5.4.2 M/M/m排队模型
- M/M/m排队模型与M/M/1排队模型不同之处在于增加了服务窗口数量。
- M/M/m排队模型由m个相同的服务窗口并行服务,顾客排成一个队列,并可以随机选择空闲服务窗口。它的顾客源数量和截止队长数量都是无限的。其系统结构如下所示。
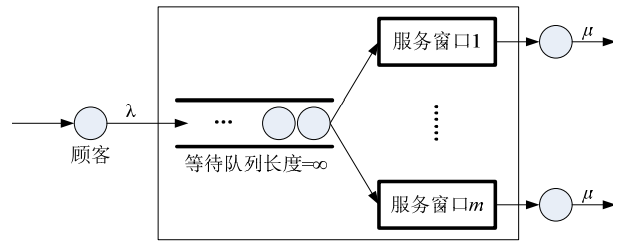
- M/M/m排队模型的顾客的到达速率为:
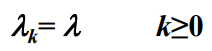
- 由于M/M/m排队模型的各服务窗口是相互独立工作的,且窗口服务速率相同,即有
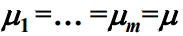 ,因此系统服务速率为
,因此系统服务速率为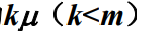 或
或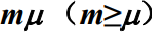 ,即:
,即:
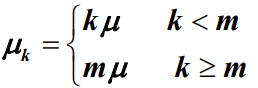
- 服务强度
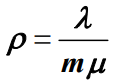 ,其状态转移图如下所示
,其状态转移图如下所示
 *
*
- 该模型是一个无限状态生灭过程。将公式(5.129)和公式(5.130)代入到公式(5.92),可以得到M/M/m排队模型的初始状态概率P0和稳态概率Pk分别为:
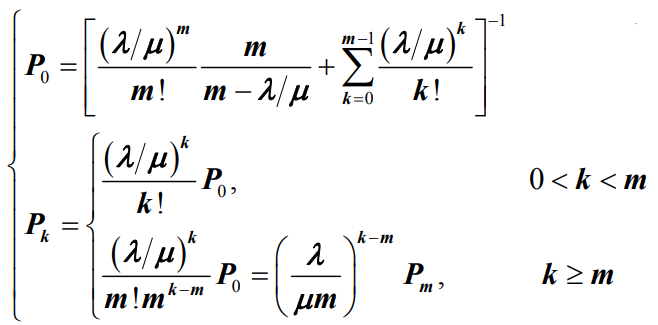
- 下面来求解平均等待队长Lq。由于只有在顾客数量大于服务窗口数量时系统中才会出现顾客排队情况,因此平均等待队长从第m+1个状态开始计算:
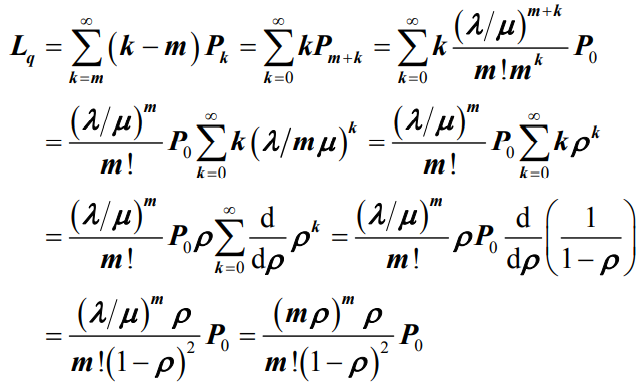
- 根据Little定理,平均队长Ls、平均逗留时间Ws和平均等待时间Wq分别为
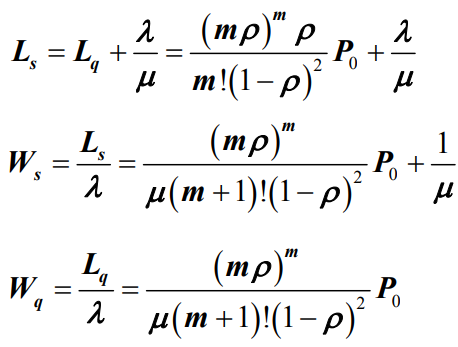
- 另一方面,平均队长Ls与平均等待队长Lq有如下关系:
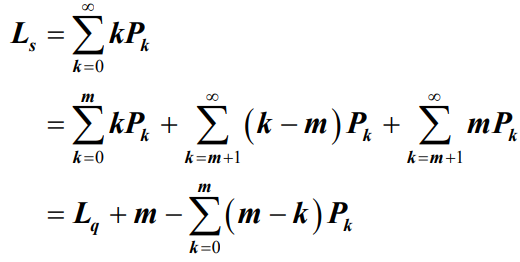
- 那么,公式是否矛盾呢?
- 分析二者的关系。根据公式可知:
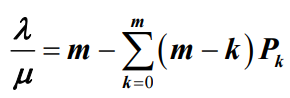
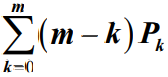 表示了平均空闲服务窗口数量,
表示了平均空闲服务窗口数量, 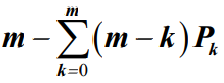 则表示了平均忙碌的服务窗口数量,μ 为窗口服务速率,
则表示了平均忙碌的服务窗口数量,μ 为窗口服务速率,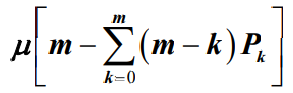 为系统服务速率,如果系统达到平衡,它应等于平均到达率 λ,因此两公式是等价的
为系统服务速率,如果系统达到平衡,它应等于平均到达率 λ,因此两公式是等价的在实际情况中,经常会遇到下面这种情况
- 若改变M/M/m排队模型的排队方式,将m个服务窗口前各设置一个队列,此时的模型就是m个M/M/1排队模型的叠加
- 那么,究竟是m个M/M/1排队模型(分别排队并列式服务)的工作效率高,还是1个M/M/m排队模型(混合排队并列式服务)的工作效率高?
- 假设服务窗口数量m=3,系统到达率 λ=0.9人/分钟,窗口服务速率 μ=0.4人/分钟,两种排队模型如下所示
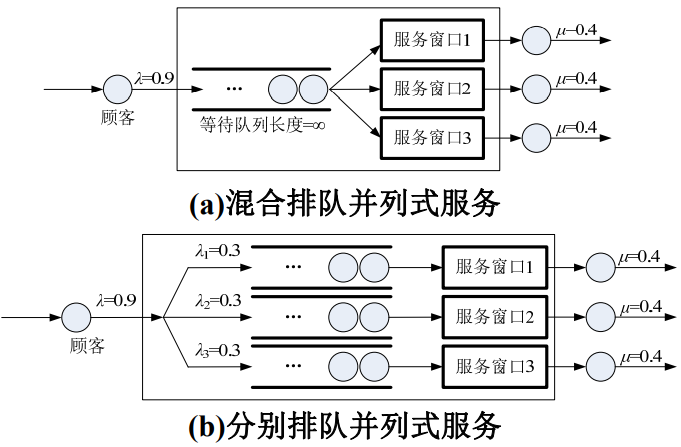
- 对于分别排队并列式服务系统来说,由于顾客进入队列后坚持不换队列,因此每个队列的平均到达率为
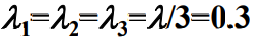 。而对于混合排队并列式服务系统来说,平均达到率为 λ=0.9。下表给出两种系统的各指标的对比
。而对于混合排队并列式服务系统来说,平均达到率为 λ=0.9。下表给出两种系统的各指标的对比
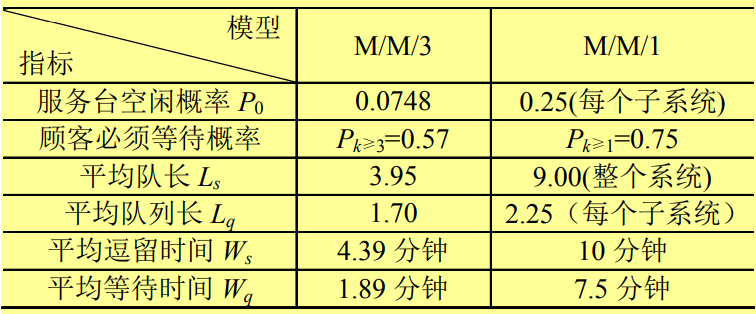
- 通过对比可知,如果系统采用混合排队并列式服务的排队方式,那么该系统将会获得更高的性能。
- 无论是服务窗口空闲概率,还是平均逗留时间和平均等待时间上来看,该排队方式都比分别排队并列式服务的排队方式更胜一筹
因此,为了获得更好的性能,通信系统应该采用该种排队方式,以减少数据交换的阻塞率和延时
5.4.3 M/M/∞排队模型
M/M/∞排队模型可以看成是M/M/m排队模型当服务窗口数量为无穷大时候的情况。
- M/M/∞排队模型由无穷多个相同的服务窗口并行服务。其系统结构如下所示。
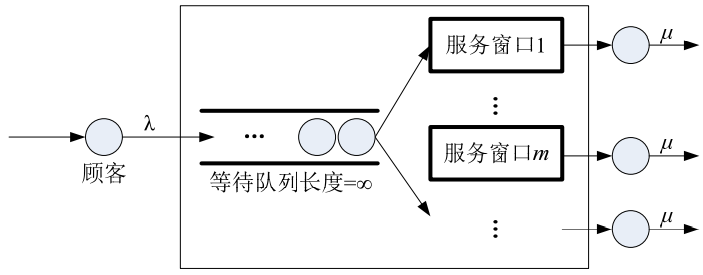
- M/M/∞排队模型顾客到达速率和系统服务速率为:
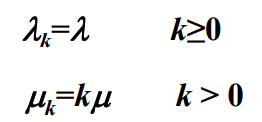
- 假设
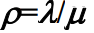 ,其状态转移图如下所示
,其状态转移图如下所示

- 根据上图可知,该模型是一个无限状态生灭过程。将公式代入,可以得到M/M/∞排队模型的初始状态概率P0和稳态概率Pk分别为
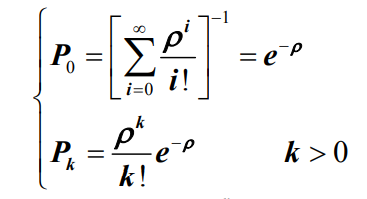
- 其中,上式用到了
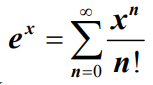 。
。 - 平均队长 Ls :
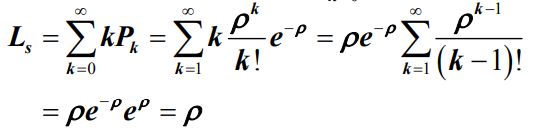
- 根据Little定理,平均等待队长Lq、平均逗留时间Ws 和平均等待时间Wq分别为
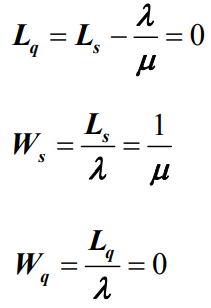
- 例题
5.4.4 M/M/1/n排队模型
- M/M/1/n排队模型是M/M/1排队模型的一种变换形式,它与M/M/1排队模型不同之处在于设置了长度为n的截止队长。其系统结构如下所示

- M/M/1/n排队模型的顾客到达速率和系统服务速率分别为:
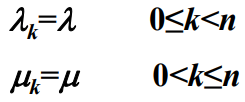
- 该系统模型同样满足参数为的泊松流输入条件,顾客的服务时间服从参数为的负指数分布。它的状态转移图如下所示。

- 该模型是一个有限状态生灭过程。根据公式,M/M/1/n排队模型服务强度为:
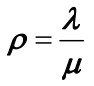
- 根据公式,系统的初始状态概率P0和稳态概率Pk分别为
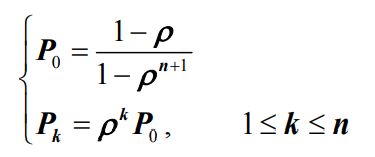
- 平均队长Ls:
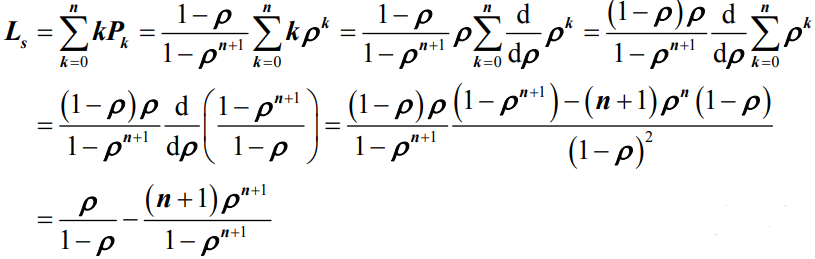
- 观察公式可以发现,当n→+∞时,平均队长
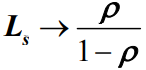 ,这和M/M/1排队模型的平均队长计算结果是一样的。也就是说当系统截止队长趋向于无穷时,M/M/1/n排队模型就转化为M/M/1排队模型
,这和M/M/1排队模型的平均队长计算结果是一样的。也就是说当系统截止队长趋向于无穷时,M/M/1/n排队模型就转化为M/M/1排队模型 - 根据公式可知:
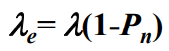
- 根据Little定理可以得到平均等待队长Lq、平均逗留时间Ws和平均等待时间Wq :
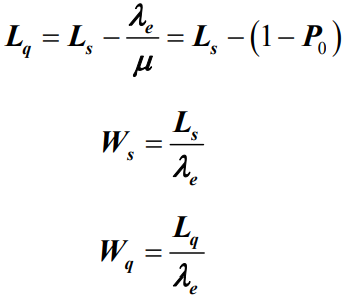
- 例题
5.4.5 M/M/m/n排队模型
- M/M/m/n排队模型是在M/M/m排队模型的基础上设置了长度为n的截止队长,等待队列长度为n-m,其系统结构如下所示。
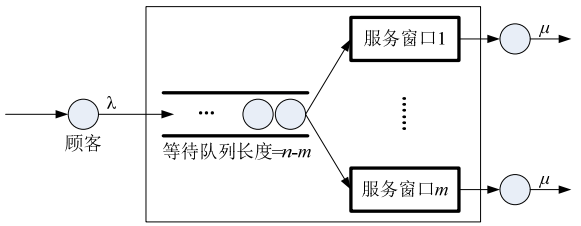
- 与M/M/m排队模型一样,M/M/m/n排队模型客户源也是无限的,因此有:
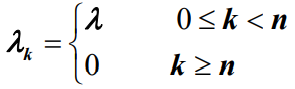
- 各服务窗口是相互独立工作的,且提供相同的服务速率。当顾客数量k小于等于服务窗口数量m时,系统实际提供服务速率为
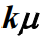 ,当顾客数量k大于服务窗口数量m时,系统实际提供服务速率为
,当顾客数量k大于服务窗口数量m时,系统实际提供服务速率为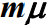 ,即系统以最大处理速度向顾客提供服务。因此系统服务速率为
,即系统以最大处理速度向顾客提供服务。因此系统服务速率为
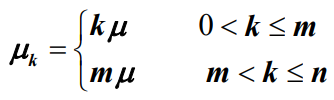
- M/M/m/n排队模型的状态转移图如下所示:

- 将公式代入可以得到系统的初始状态概率P0和稳态概率Pk分别为
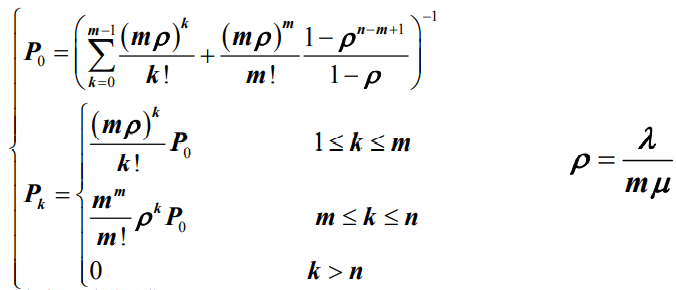
- 下面来看平均等待队长Lq:
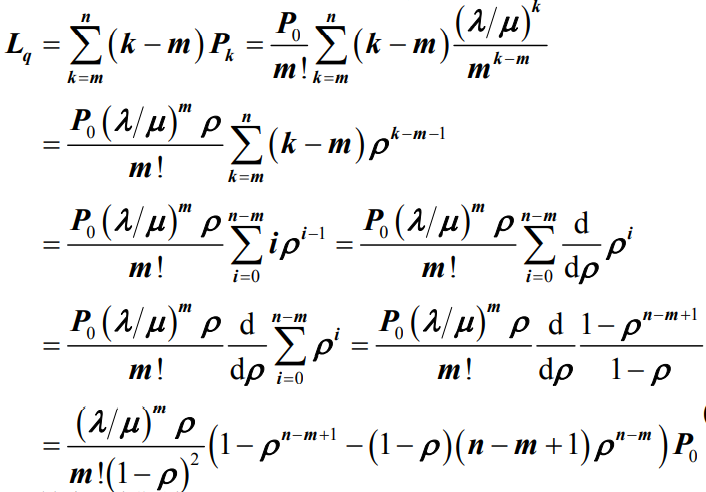
- 根据公式可知
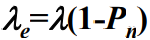 ,因此由Little定理可以求出平均队长Ls、平均逗留时间Ws和平均等待时间Wq分别为
,因此由Little定理可以求出平均队长Ls、平均逗留时间Ws和平均等待时间Wq分别为
5.4.6 M/M/m/m排队模型
- M/M/m/m 排队模型是M/M/m/n排队模型的一种特殊形式。
- 等待队列长度等于零,进入系统的顾客直接进入到各个服务窗口。当所有服务窗口均有顾客接受服务时,新来的顾客将被拒绝进入系统。
- 其排队模型结构如下所示。
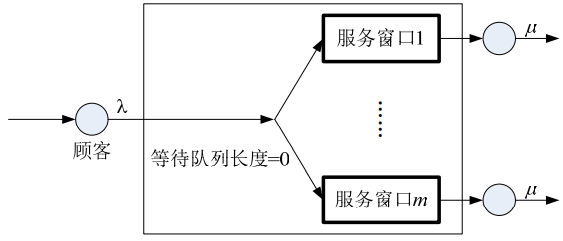
- M/M/m/m排队模型也是客户源是无限的,因此有:

- 各服务窗口是相互独立工作的,且提供相同的服务速率。
- 当顾客数量k小于等于服务窗口数量m时,系统实际提供服务速率为μ ,当顾客数量k大于服务窗口数量m时,系统实际提供服务速率为mμ ,即系统以最大处理速度向顾客提供服务:

- M/M/m/m排队模型的状态转移图如下所示

- 令公式
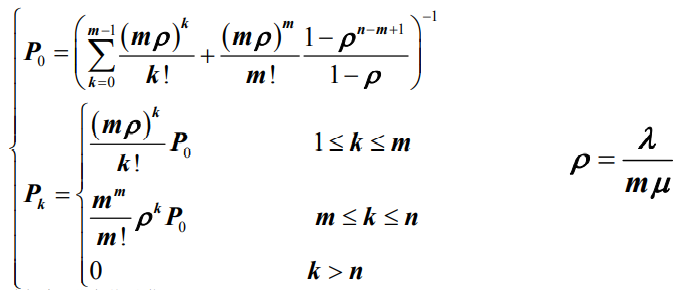 中n=m,即可以得到系统的初始状态概率P0和稳态概率Pk分别为:
中n=m,即可以得到系统的初始状态概率P0和稳态概率Pk分别为:
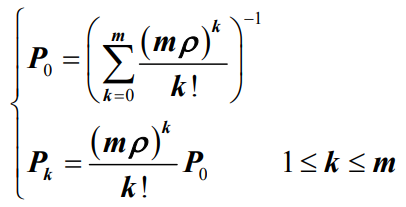
- 将n=m代入到公式
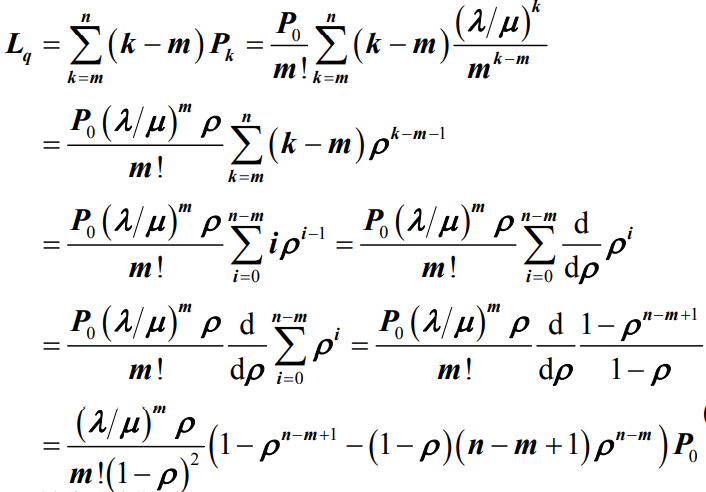 可以得到平均等待队长Lq
可以得到平均等待队长Lq
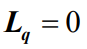
- 根据公式
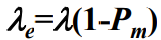 ,通过Little定理可以求出平均队长Ls、平均逗留时间Ws和平均等待时间Wq 分别为
,通过Little定理可以求出平均队长Ls、平均逗留时间Ws和平均等待时间Wq 分别为
5.4.7 M/M/1/∞/c排队模型
- 前面研究的排队模型都是属于顾客源无限情况。下面来分析顾客源是有限的排队模型。M/M/1/∞/c排队模型是一种最简单的顾客源有限的排队模型。
- 需要注意,分析该排队模型的时候,不能像分析M/M/1/n排队模型那样简单地认为是在M/M/1排队模型的基础上设置了顾客源数量。根据前面分析可知,当顾客源有限时,顾客到达率是每个客户的平均到达率。M/M/1/∞/c排队模型结构如下所示。
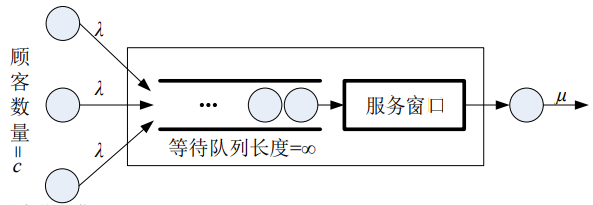
- 由于顾客源有限,随着顾客不断到达排队系统,顾客将越来越少,到达速率也将越来越小。当所有顾客全部到达系统后,顾客到速率为零,即有:
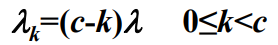
- 对于服务窗口来说,只要有顾客到达,系统就将全速为顾客提供服务,既有:

- 其状态转移图如下所示

- 将公式代入可以得到系统的初始状态概率P0和稳态概率Pk分别为:
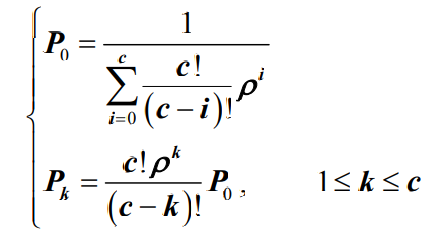
- 其中,
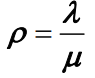
- 下面来看M/M/1/∞/c排队模型的主要性能指标。根据公式有
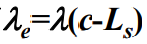 ,又因为根据统计平衡原理有
,又因为根据统计平衡原理有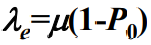 ,因此平均队长Ls是:
,因此平均队长Ls是: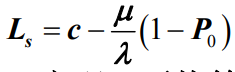
- 这样,根据Little定理,平均等待队长Lq、平均逗留时间Ws和平均等待时间Wq分别为:
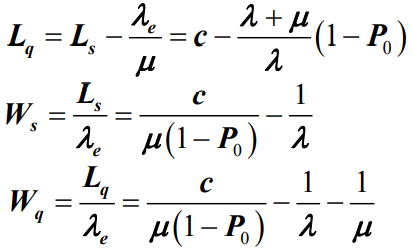
- 例题
5.4.8 M/M/m/∞/c排队模型
- M/M/m/∞/c排队模型也是一种顾客源有限的排队模型,且有m<c。顾客到达率λ仍然是每个客户的平均到达率。M/M/m/∞/c排队模型结构如下所示。
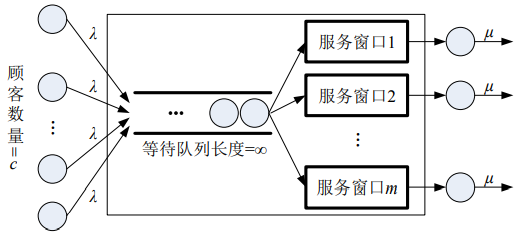
- 顾客到达率和M/M/1/∞/c排队模型分析的一样,即有:
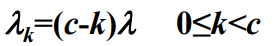
- 对于服务窗口来说,当到达系统的顾客数量k小于等于服务窗口数量m时,系统所能提供的服务速率为kμ ,当到达系统的顾客数量k大于服务窗口数量m时,系统将全速为顾客提供服务,既有:
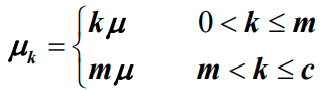
- 系统的状态转移图如下所示

- 将公式代入可以得到系统的初始状态概率P0和稳态概率Pk分别为
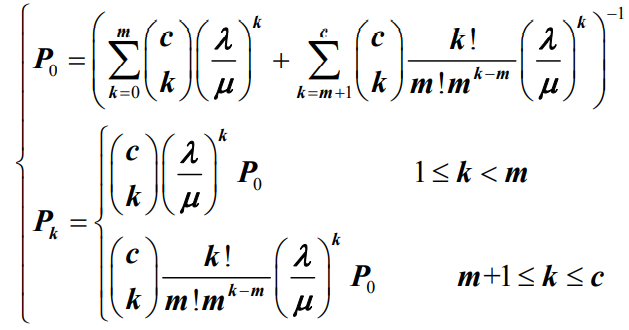
- 其中
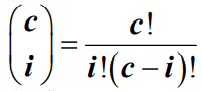
- P0和Pk的求解过于复杂,通常情况是采用查表的方法。因此,平均等待队长Lq只给出一般结论:
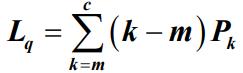
- 系统有效到达率为
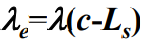 ,根据Little定理可得
,根据Little定理可得
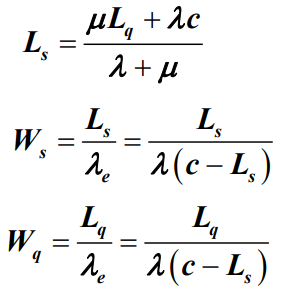
- 例题
5.4.9 M/M/m/m/c排队模型
- M/M/m/m/c排队模型在M/M/m/∞/c排队模型的基础上设置了队列长度,它也是一种顾客源有限的排队模型,且一般有m<c。顾客到达率仍然是每个客户的平均到达率。等待队列长队为零,M/M/m/m/c排队模型结构如下。
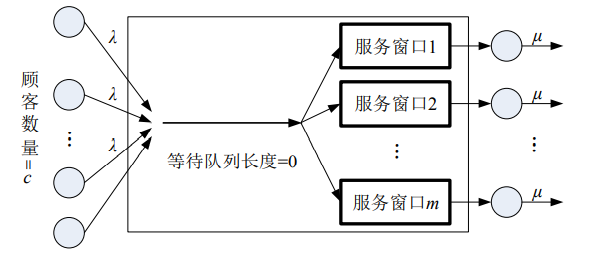
- 顾客到达率:
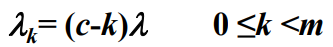
- 系统提供的服务速率:

- 系统的状态转移图如下所示

- 将公式代入可以得到系统的初始状态概率 P0和稳态概率Pk分别为
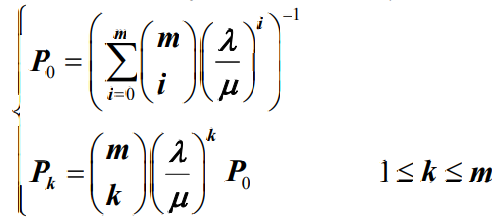
- 其中,
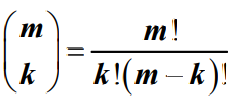
- 等待队长应当在窗口全部占满时出现,而此时等待队长,因此平均等待队长Lq
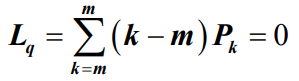
- 根据公式可知,系统有效到达率为
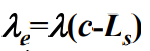 。
。 - 这样,根据Little定理可以求出平均队长Ls为:
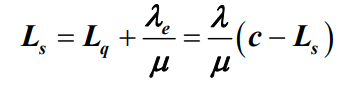
- 因此,平均队长Ls为
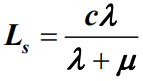
- 根据Little定理,平均逗留时间Ws和平均等待时间Wq分别为:
5.4.10 M/M/m/c/c排队模型
- M/M/m/c/c排队模型也是一种顾客源有限的排队模型,它和M/M/m/m/c排队模型的区别体现在等待队列长度。由于m<c,因此,等待队列长度为c-m。顾客到达率 λ 仍然是每个客户的平均到达率。排队模型结构如下所示
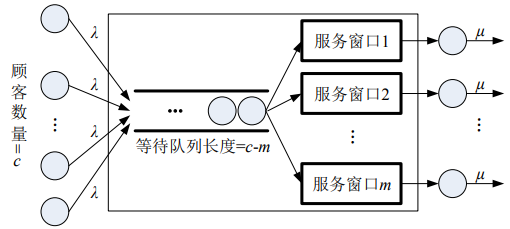
- 由于等待队列长度不为零,因此顾客到达率主要取决于顾客数量c
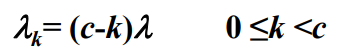
- 系统服务速率主要取决于服务窗口数量 :
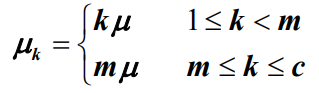
- 状态转移图如下所示

- 将公式代入可以得到系统的初始状态概率P0和稳态概率Pk分别为
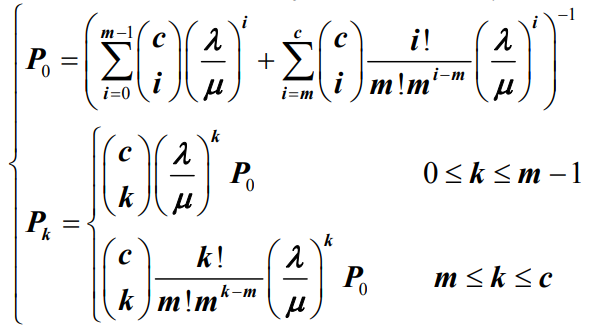
- 其中,
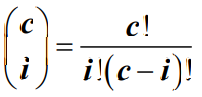
- 平均队长Ls为:
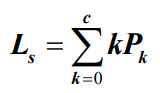
- 根据公式(5.110)可知,系统有效到达率为
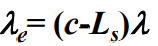 。这样,根据Little定理可以求出平均等待队长Lq、平均逗留时间Ws和平均等待时间Wq分别为:
。这样,根据Little定理可以求出平均等待队长Lq、平均逗留时间Ws和平均等待时间Wq分别为:
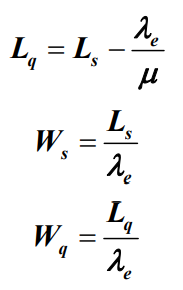
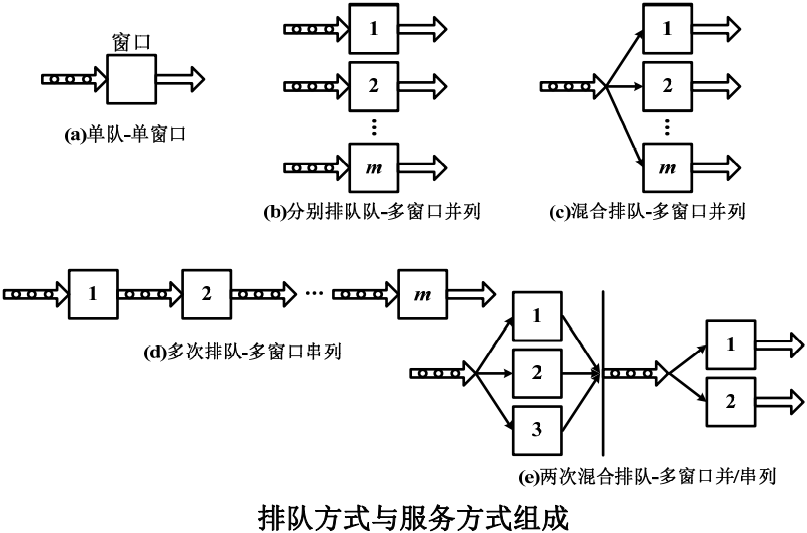
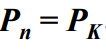 。
。