1. 信源编码
1.1 概述
- 通信系统的有效性最直观的体现方式就是信息传输速率,也就是单位时间内传递的信息量
- 信息传输速率主要取决于三个方面的因素,分别是符号速率,信源熵和噪声熵
- 符号速率与信道带宽有关,一般根据应用需求来确定,噪声熵与信道条件有关,由应用环境确定,而且两者也与系统成本有关。
- 提高信源熵是提高通信系统有效性的一个重要途径,也就是提高信源单位符号所携带的信息量。
1.1.1 信源编码的作用
- 提高通信的有效性。压缩信源的冗余度。(信源的不等概带来的)
- 压缩每个信源符号的平均比特数。(使一个符号传输足够多的信息)
1.1.2 无失真信源编码
- 实质上是统计匹配编码,根据信源符号的不同概率分布选择匹配的码
1.1.3 信源统计剩余度
- 无记忆信源
- 概率分布的非均匀性
有记忆信源
- 符号的相关性及符号概率分布的非均匀性
压缩信源冗余度
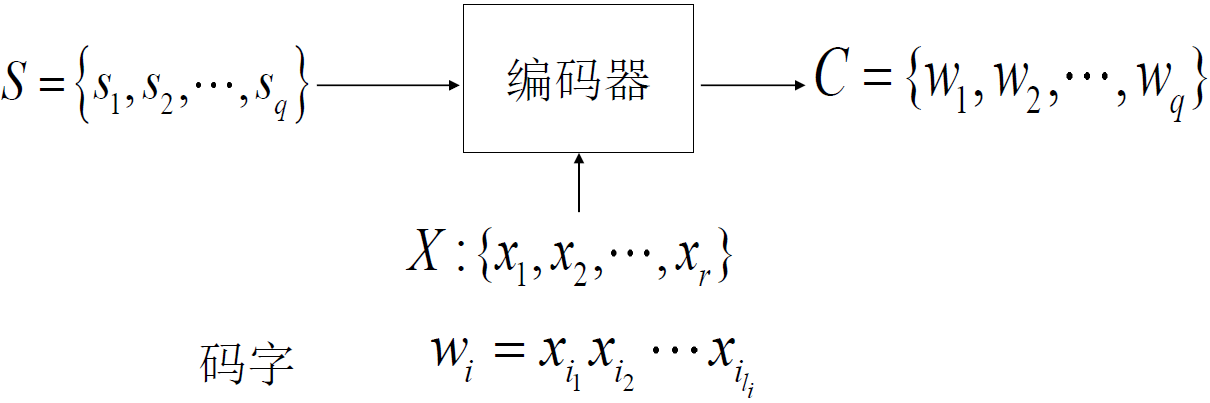
解释:
- 信源单符号
有
种可能
- 每种可能需要与码字
对应,然后送到信道上
- 每一个码字是由编码器编码完成映射,由码符号
组成,长度为
1.3 N次扩展码
信源符号S的N次扩展视为,N个信源符号的排列组合
对应的码字的N次扩展视为,N和码字的排列组合
1.4 编码术语
- 码字:码符号序列
- 码长:一个码字的码符号个数,即
- 码组:全体码字的集合
- 定长码:一个码中所有码字的码长相等
- 变长码:一个码中不是所有码字的码长都相等
1.5 奇异码
- 若信源符号和码字是一一对应的,为非奇异码,否则为奇异码
- 奇异码无法完成正常的传输,存在同一码字对应不同信源的情况
1.6 唯一可译性
- 任意一串有限长的码符号序列只能被唯一地译为对应的信源符号序列,则为唯一可译码(单义可译码、异前置码)
- 需要满足
- 码字与符号是一一对应的(即奇异码不具备唯一可译性)
- 不同的信源符号序列对应不同的码字序列(编码唯一性)
- 非奇异码不一定是唯一可译的
- 非奇异码+等长码⇨唯一可以码
- 非唯一可译性常常存在于不等长码时,起始的码字由几个码符号组成不确定,有不同的翻译结果
1.7 即时码
1.7.1 即时码的判断
- 某个唯一可译码在接收到一个完整的码字时无需参考后续的码符号就能立即译码,称为即时码
-
1.7.2 即时码的构造
即时码的构造方法
- 树图法
- 将码字安排在终端节点上
码树分类
树根——码字起点
- 分支数——码的进制数
- 节点——码字或码字的一部分
- 终止节点——码字
- 节数——码长
- 非满树——变码长
满树——等码长
[x] 例题
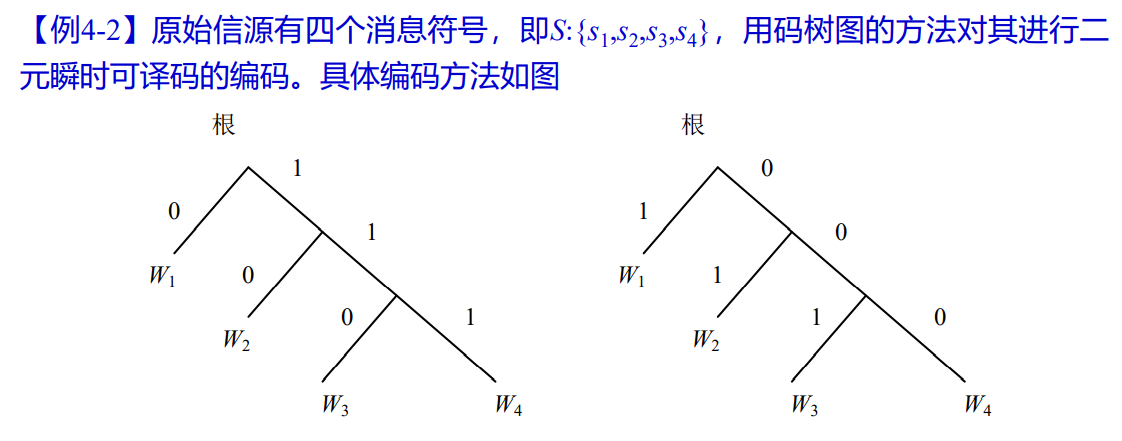
- 构成的瞬时可译码是不唯一的
- 同样可以用于多元编码
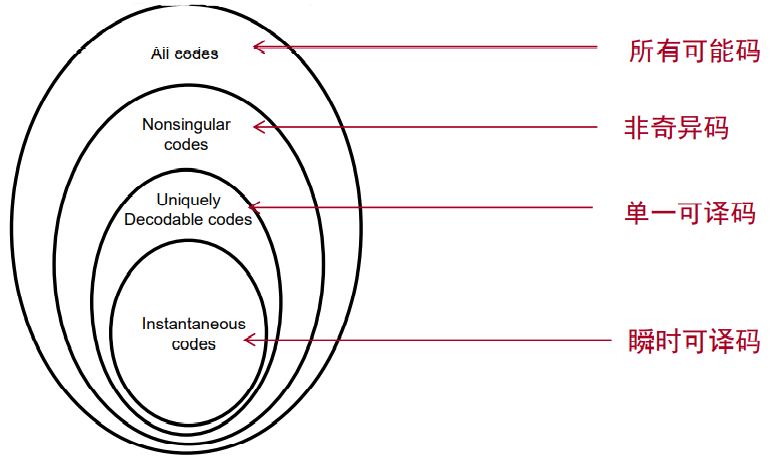
1.8 相互关系

2. 定长码及定长信源编码定理
2.1 唯一可译长码存在条件
- 非奇异码
- 定长码
- 唯一可译码
信源符号集有个符号,码符号集
种码元,定长码码长
需要满足
N次扩展信源后需要满足
2.2 定长信源编码定理
如果不考虑符号间的依赖关系
码长为
若考虑符号间的依赖关系,对不可能出现的符号不进行编码,可以缩短码长
求定长信源编码所需码长的极限值
个码元承载的信息量要大于N个信源信号的信息量
只要满足这个条件,就可以实现无错通信
定长编码定理同样适用于离散平稳有记忆信源,需要将信源熵改为极限熵
定义
代表每个信源符号编码后能载荷的最大信息量
2.3 信源序列长度界限
- 在已知方差
和信源熵
的条件下,要达到最佳编码效率
并且允许的译码错误概率小于任一给定的正数
,信源序列的长度
存在一定的要求
解释(求解):
解释(求解):
3. 变长码及变长信源编码定理
3.1 Kraft不等式
- 即时码和唯一可译码存在的充要条件:
- 此为存在性证明不能当作判断性证明
- 变长码要成为唯一可译码,不仅本身应是非奇异的,它的有限长次扩展码也应该是非奇异的
- 例题
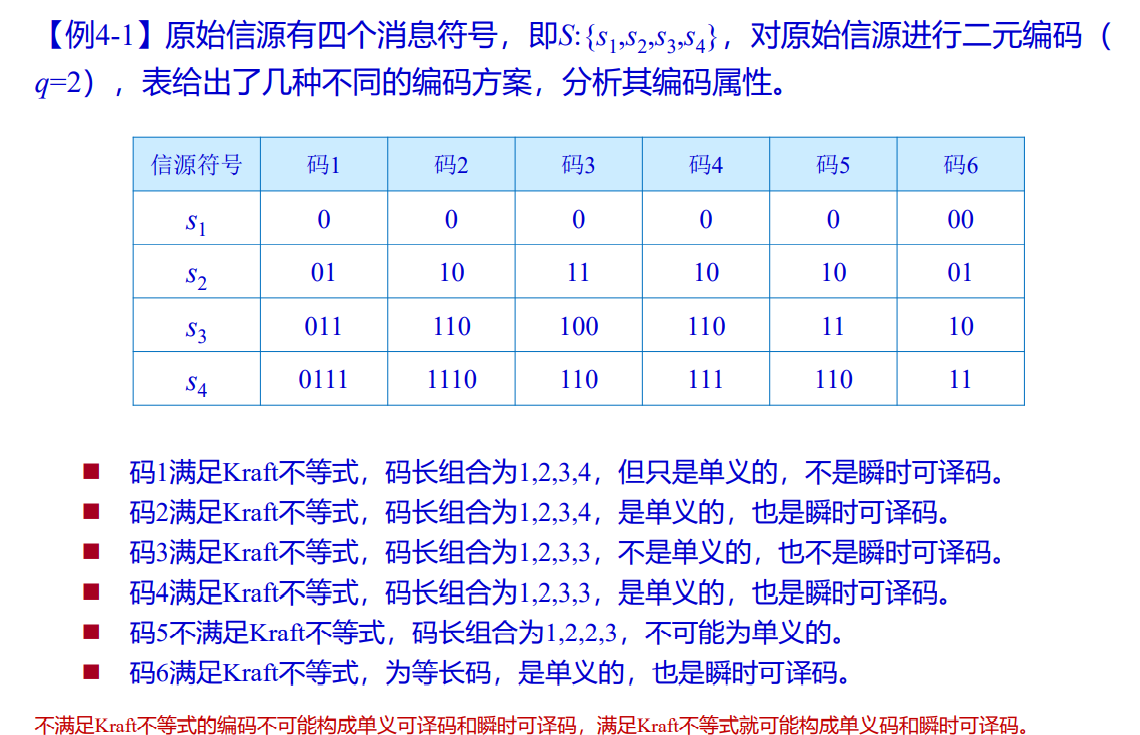
3.2 变长唯一可译码的判别
- 构造F1 :
- 考察C中所有码字,如果一个码字是另一个码字的前缀,则将后缀作为F1 中的元素。
- 构造Fn:
- 将C 与Fn-1比较。如果 C 中有码字是中元素的前缀,则将相应的后缀放入Fn中;
- 同样Fn-1中若有元素是C 中码字的前缀,也将相应的后缀放入Fn中。
- 检验Fn
- 如果是 空集 ,则断定码C 是唯一可译码,退出循环;
- 反之,如果 Fn 中的某个元素与 C中的 某个元素相同 ,则断定码C不是唯一可译码,退出循环。
- 如果上述 两个条件都不满足 ,则为唯一可译码。
3.3 紧致码平均码长界定定理
- 平均码长
- 对于无噪声信道来说,如果假设信源符号速率r=1,信息传输率R(熵速率)即单位时间内传输的信息量就等于信源熵H(S)
- 原始信源S 经过信源编码器之后,原始信源符号集S:{s1,s2,…,sn}经过映射变换为由信道码元表示的码字符号集W:{W1,W2,…,Wn}。这时在接收机看来,信源已经是一个由信道码元符号集A:{a1,a2,…,aq}表示的新的信源A,这时的信息传输率为
- 当原始信源一定时,编码后的平均码长越小,信息传输率越高,实际上也就是编码效率越高
因此,编码效率可以用平均码长来描述。
存在唯一可译码的平均长度小于所有其它码,则称这种码为紧致码或最佳码
紧致码平均长界限定理
- 解释(单符号信源):
- 取第
个信源符号,对应第
个码字,码字长度为
- 满足:



证明编码原则:
- 符号概率越小,其对应编码的码长越长
- 符号概率越大,其对应编码的码长越短
数据压缩的极限:对于二元编码,数据压缩的极限是平均码长等于熵H(S)
这种编码规则下存在即时码,存在唯一可译码吗?
- 证明:
- 满足唯一可译长码存在条件
3.4 无失真变长信源编码定理
3.4.1 香农第一定理
离散无记忆信源熵,N次扩展信源
,对其编码,
- 平均码长
- 此时信源符号的组合有
种可能
- 平均码长界限定理
- 解释(多符号信源)(核心公式,后面都可由此公式推导得出)
- 当
- 表明当将离散无记忆信源进行N次扩展后再进行编码,就可以使原始信源每个符号的平均码长接近信源熵H(S),即平均码长趋近于下限值
- 这时并不要求原始信源的先验概率满足某种特殊分布,但却要求扩展次数N趋于无穷
- 因此,这也是一个极限定理,实际上这种方法是一种概率均匀化方法
- 推广到平稳遍历有记忆离散信源
- 满足
- 例题



- 对于有记忆信源,存在定理

- 香农编码的基本思想:用时间和计算换取效率
- 即数据压缩定理
在机器学习领域,根据香农第一编码定理和贝叶斯准则有一个最小描述长 度(MDL-Minimum description length)方法,基本思想是一样的
3.4.2 编码速率(编码信息率)
即平均每个信源符号在编码后具有的信息量
则香农第一定理的实质上是,在编码后每个信源符号的信息量要大于信源符号自身的信息量
3.4.3 编码后的信息传输率(码率)
- 即编码后平均每个码符号具备的信息量
因为
所以满足
信息传输率小于信道容量
区分:N次扩展后的信源编码后的组合码字长度
:将N次扩展后的信源编码后的组合码字长度,平均到单个信源符号编码,的码字长度
3.4.4 编码效率
- 即信源符号自身的信息量,在编码后每个信源符号具备的信息量中,的占比
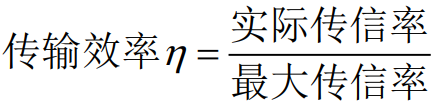
- 熵速率与信道容量之比为传输效率,传输效率是一个通信系统(点对点信道)的实际信息传输能力与最大信息传输能力的比值
- 在无噪声情况下:
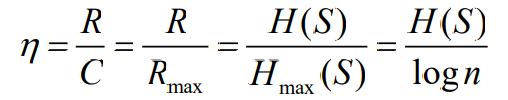
- 无编码可以认为是n元编码,其最大熵就是logn
- 有效性
3.4.5 编码效率的极限
4. 变长码的编码方法
4.1 香农码
- 编码步骤
- 将信源符号按概率从大到小顺序排列
- 按下式计算第i个符号对应的码字的码长(向上取整),确保是唯一可译码
- 计算第i个符号的累加概率
- 将累加概率变换成二进制小数,取小数点后
位数作为第i个符号的码字。
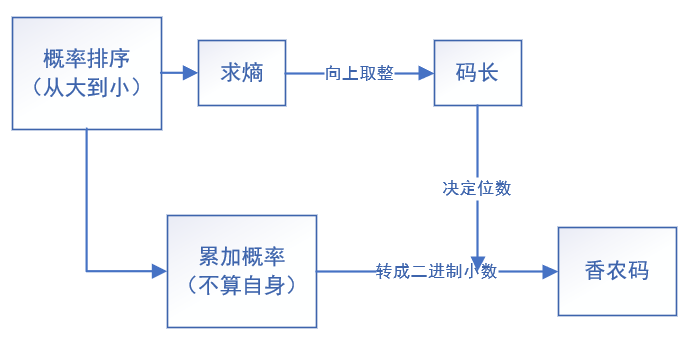
- 香农码是即时码,但冗余度稍大,不是最佳码
4.2 香农-费诺-埃利斯编码
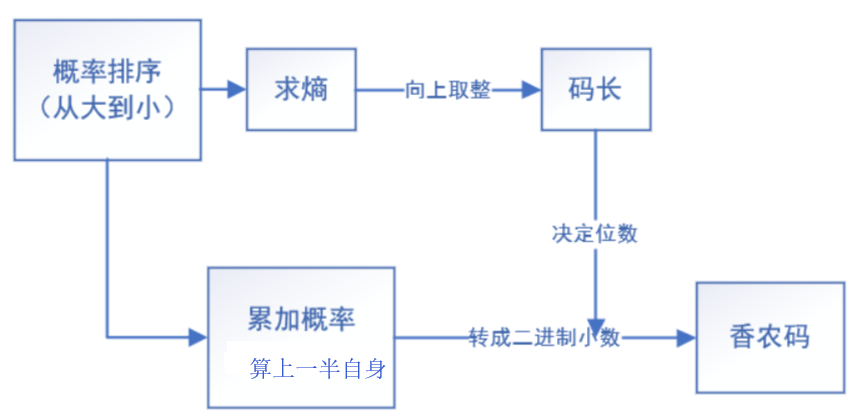
- 修正累加概率,加上了
- 码长的计算方法修正
- 其它步骤与香农码一致
4.3 Huffman码
- 从大到小排列
- 两个最小概率,编码
- 两个概率求和,视为一个源,重排
- 直至最后剩两个
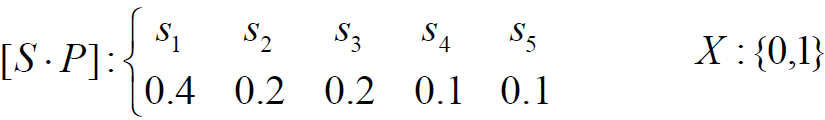
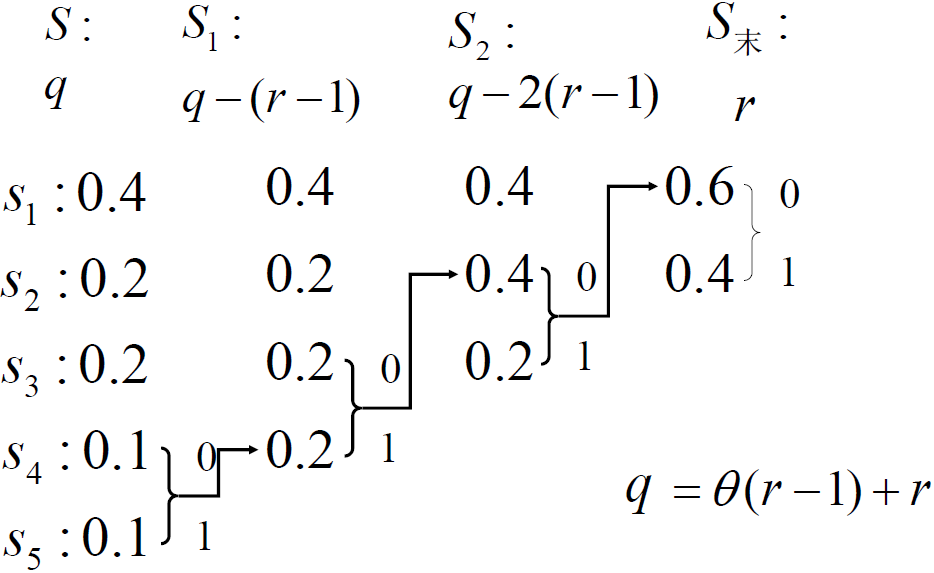
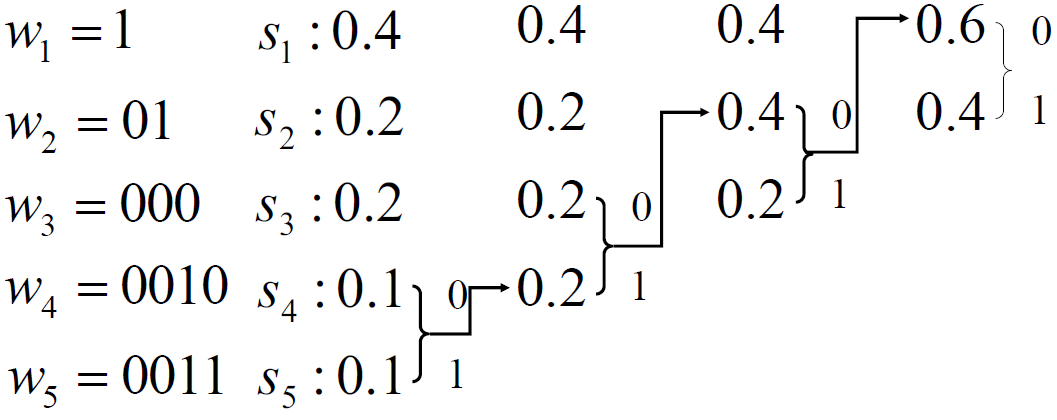
- 重排时位置不同,编码结果不同, 霍夫曼编码得出的码字不唯一
- 不影响平均码长,但影响码长的方差(码字的长度变化)
- 如果编码,概率重排时,相同概率排到最前
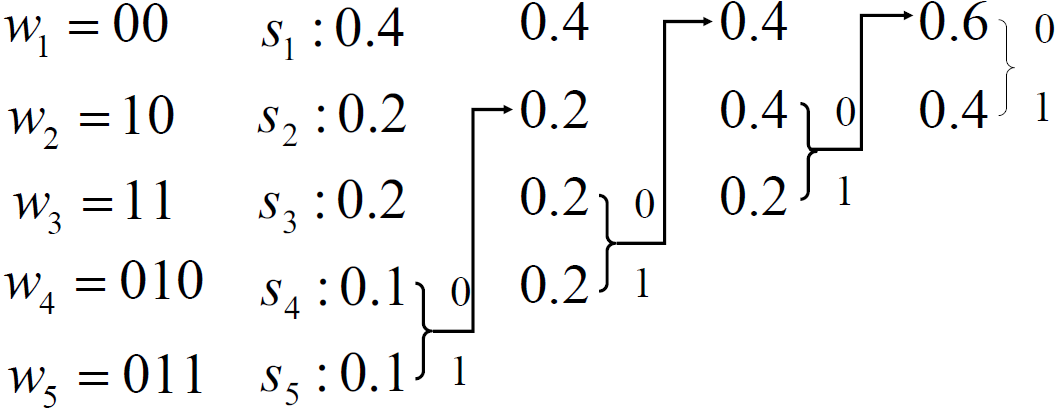
- 第二种方法编出的码字长度变化小,便于实现
- 霍夫曼码是紧致码
- 是否采用了霍夫曼码编码判断
- 是即时码
- 以二叉树展开,保证二叉树是最简洁方式
- 例题
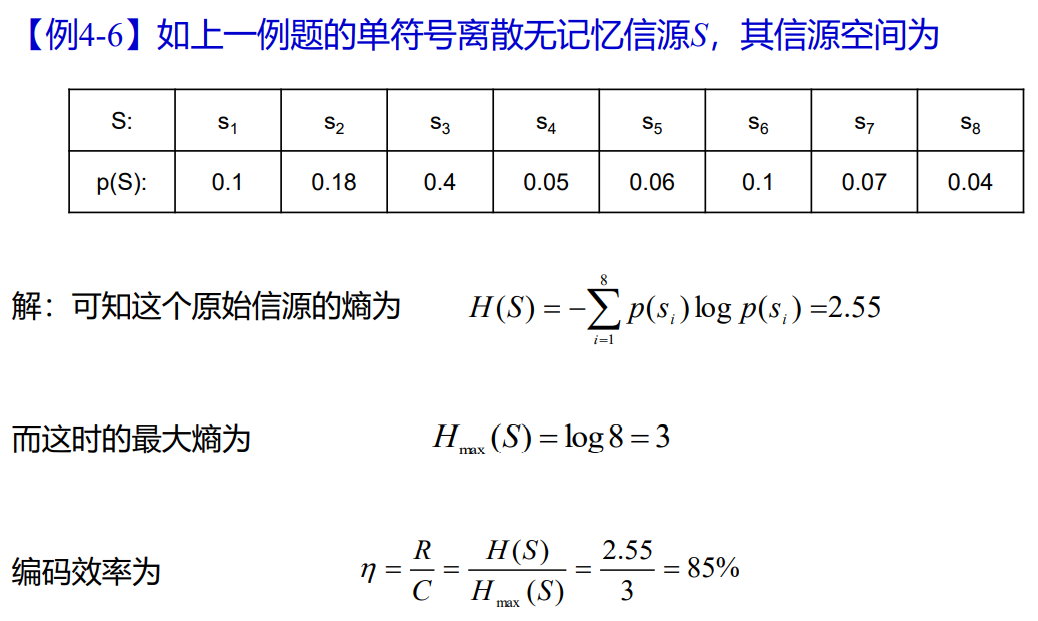
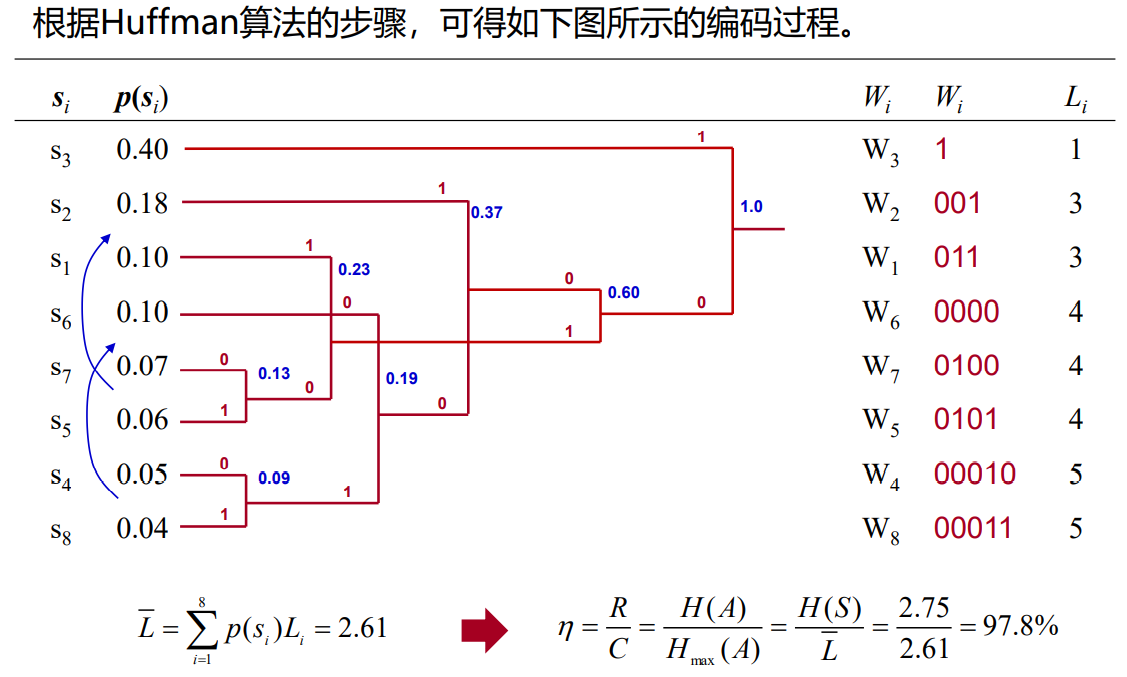
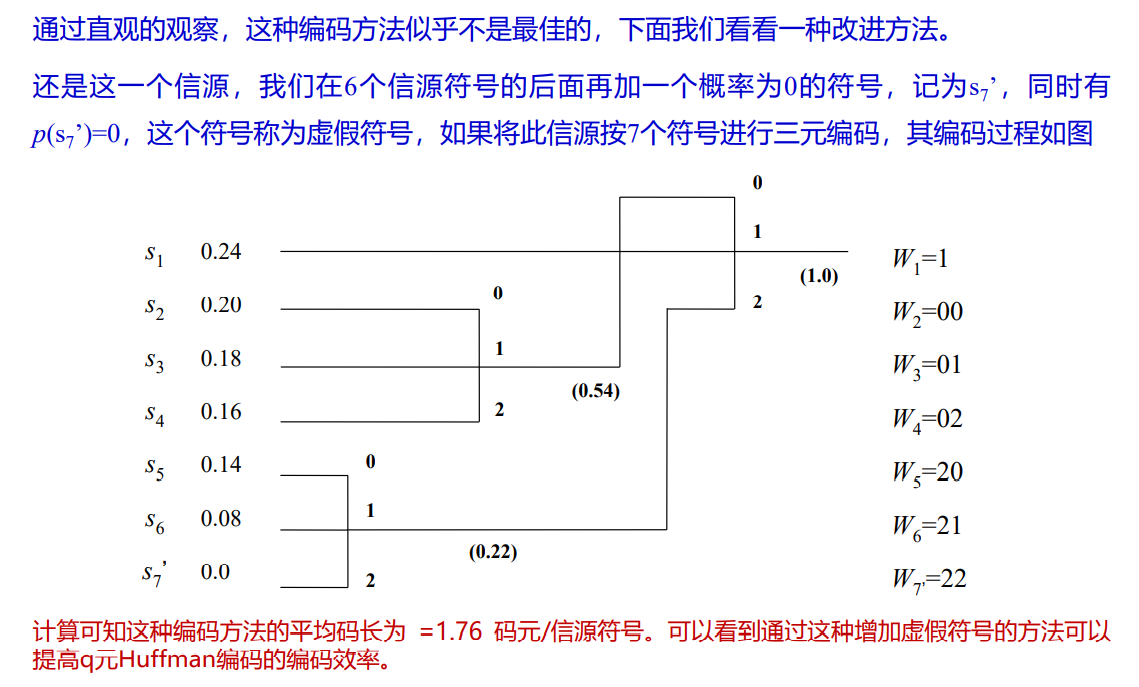
- 多元Huffuman编码算法
- 需要借助虚假符号
- 例题
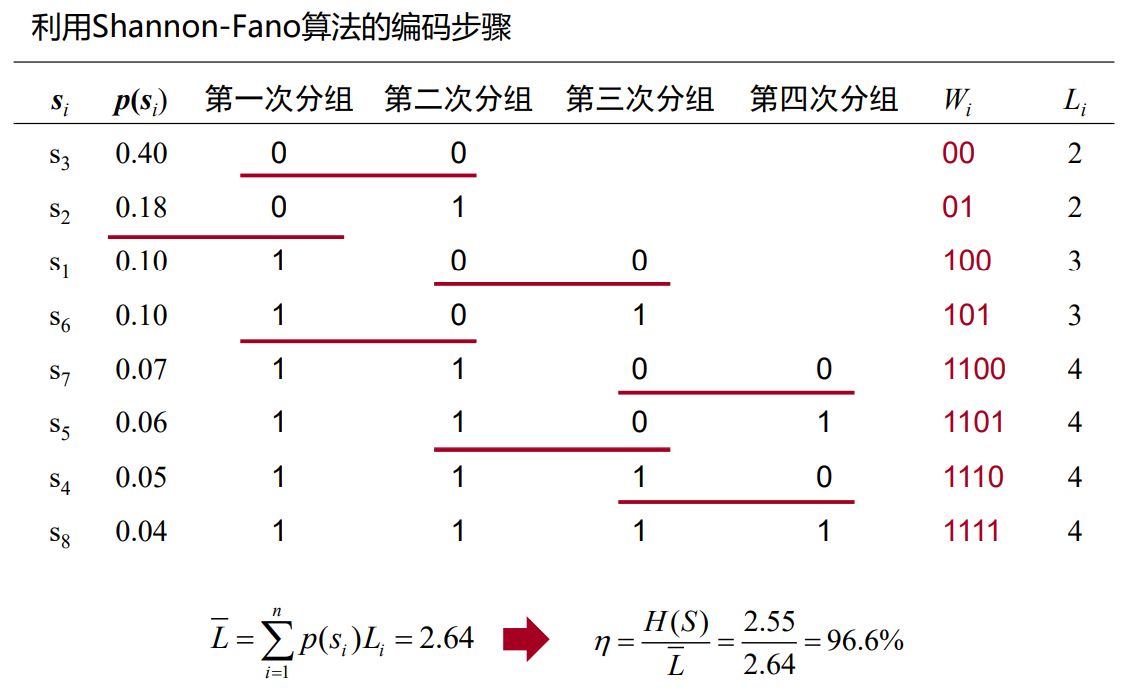
4.4 Fano码
- 从大到小排列
- 按概率分组,使每组概率和尽可能接近或相等
- 分配码元
- 再二分
- 直至不可分
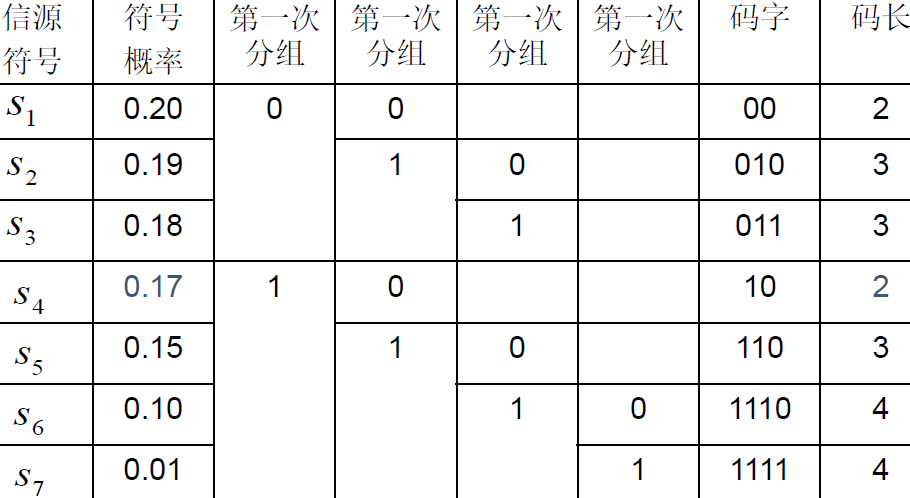
- 例题