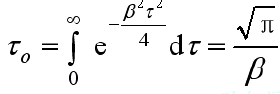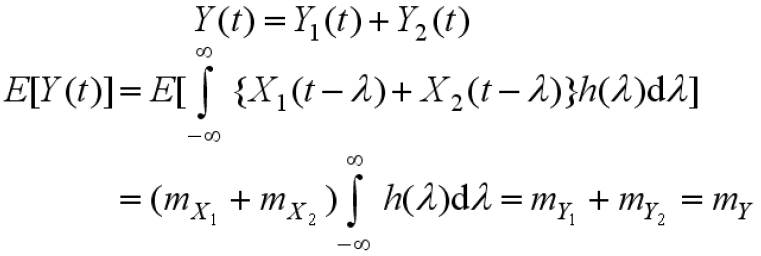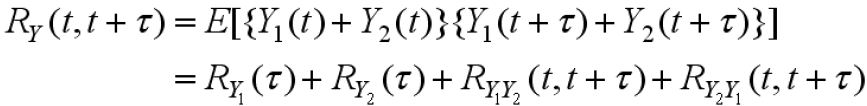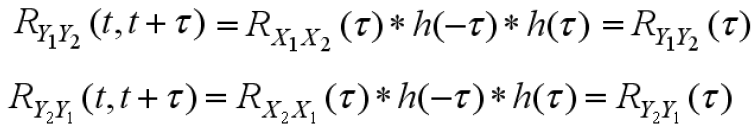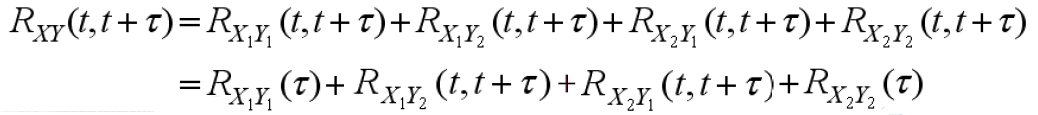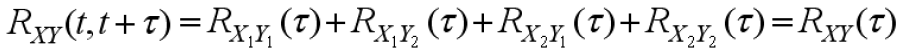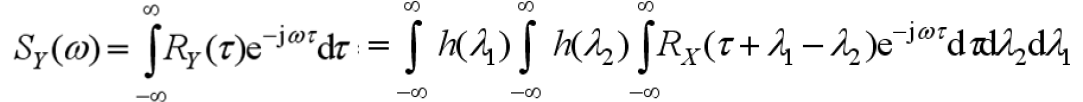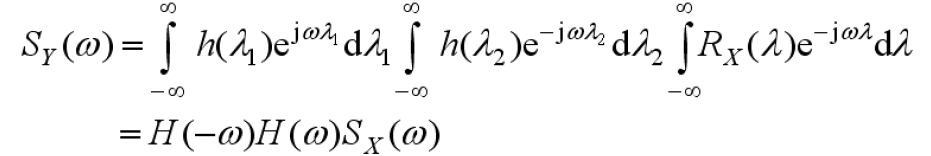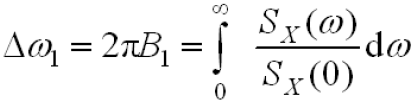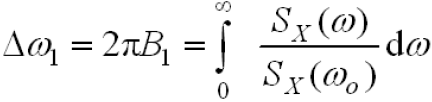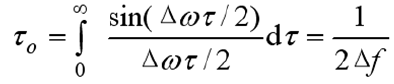1. 线性系统的响应

• 线性系统性质：

  • 齐次性，叠加性
  • 线性时不变性
  • 物理可实现性（因果性）
  • 稳定系统（输入有界，输出有界）

    1.1 对确定信号的响应

• 时域分析

• 对于因果系统，因果信号

• 离散信号

• 对于因果系统，因果信号

• 频域分析

1.2 对随机信号的响应

• 对于时域分析，积分要用均方积分

• 对于频域分析，需要对输入和输出的功率谱分析

• 时域分析

• 取其中一个样本函数

• 得到一个确定的时间函数
• 对随机过程中所有的样本处理，得到另一个随机过程的所有样本
• 可以表示为

• 因果系统

• 卷积积分存在的条件：此均方积分处处收敛
• 离散信号

• 因果系统

2. 线性系统输出的统计特征

2.1 系统输出的概率分布

• 输入为高斯过程
• 通过一个系统（低通，高通，带通……）

• 输出也为高斯过程

• 输入为非高斯过程

• 当输入随机过程的功率谱带宽远大于系统带宽时
  • 系统输出的随机过程接近高斯分布

• 当输入随机过程的功率谱带宽远小于系统带宽时

  • 系统输出的随机过程接近输入随机过程的概率分布（全通滤波器）

    2.2 系统输出的数学期望

• 时域分析法：直接定义式积分求解

• 为平稳随机过程，均值为

2.3 系统输出的自相关函数

• 一般随机过程

• 平稳随机过程

• 因此，如果输入随机过程为平稳时，输出随机过程也平稳
• 输出自相关函数等于输入自相关函数与系统冲击响应的二次卷积
• 若输入随机过程是严平稳的，系统的输出也将是严平稳的

• 若输入是各态历经过程，输出也具有各态历经性

  2.4 系统输出的互相关函数

• 系统的输入输出是相关的，用互相关函数描述

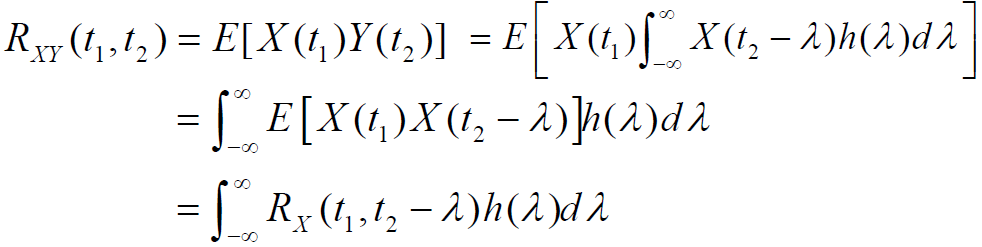
• 如果输入是平稳随机过程，输出也是平稳随机过程

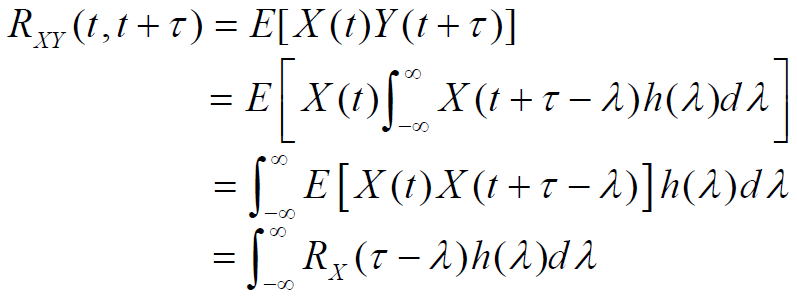
• 结合系统输出的自相关函数，存在关系

• 用图描述
  • 一般随机过程

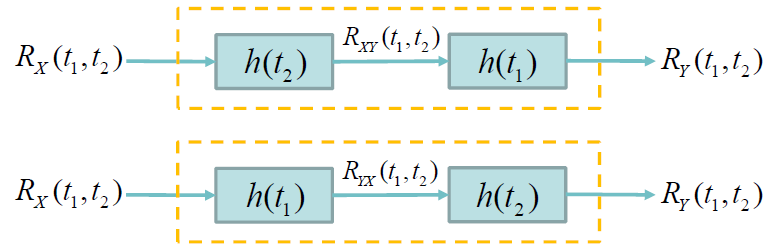
• 平稳随机过程

• 可以用于计算系统冲激响应的估值

  • 各态历经性下，输入输出互相关的时间平均等于统计平均
  • 即得到的XY的互相关函数
  • 输入通过一次系统即得到互相关函数，即可由互相关函数和输入得知系统函数

    2.5 系统输出为随机过程的加性噪声

    
    
    

    2.5.1 数学期望

    

    2.5.2 自相关函数

    
    其中
    
    

• 

  2.5.3 输入与输出的互相关

  
  其中
  
  

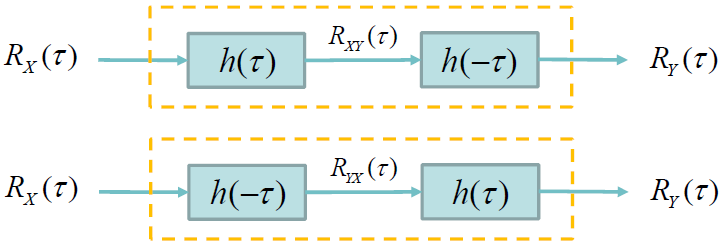
3. 线性系统输出的功率谱密度

• 时域计算
  • 输出自相关函数

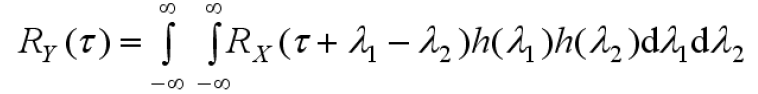
• 输出功率谱密度

3.1 计算输出的功率谱密度公式

• 对应理解

输出平均功率：

• 对比确定信号

• 通过功率谱密度做逆变换再求输出的自相关函数，要比卷积运算量小

3.2 计算输入与输出的互功率谱密度

4. 典型线性系统对随机信号的响应

4.1 等效噪声带宽

• 信号带宽：表示信号频谱在频率轴上所占有的宽度
• 系统带宽：表示系统对信号频谱的选择性

4.1.1 3dB带宽

• 低通信号：时的值，即时的值，称为半功率带宽
• 带通信号：频带两个边缘幅度为之间的宽度

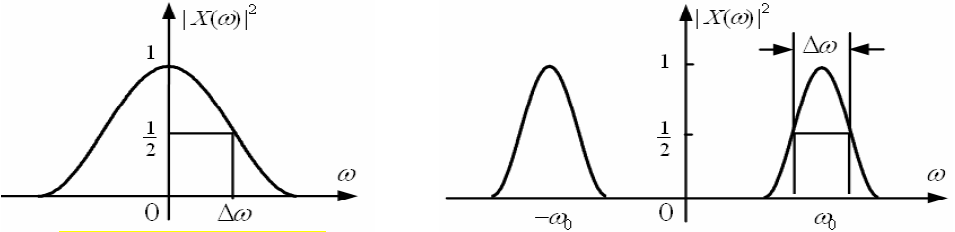
• 角频率做横轴，带宽用表示

• 频率做横轴，带宽用表示

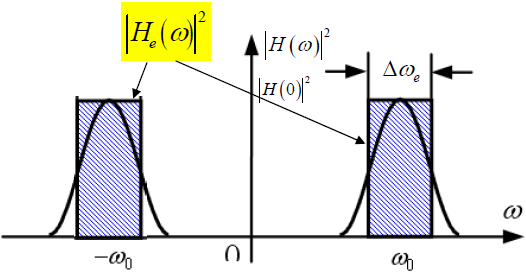
  4.1.2 矩形带宽

  确定信号带宽

• 等效带宽，将信号的会议话幅度谱等效为一个矩形，矩形宽度为矩形带宽（正频率部分）

• 等效原则：
  • 等效前后的面积不变（能量不变）
  • 等效后矩形的高度为其最大值
• 低通信号：
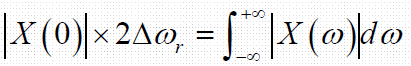
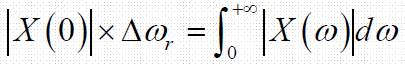
• 带通信号：

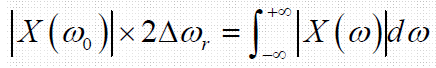
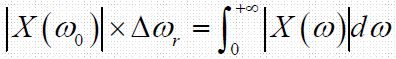
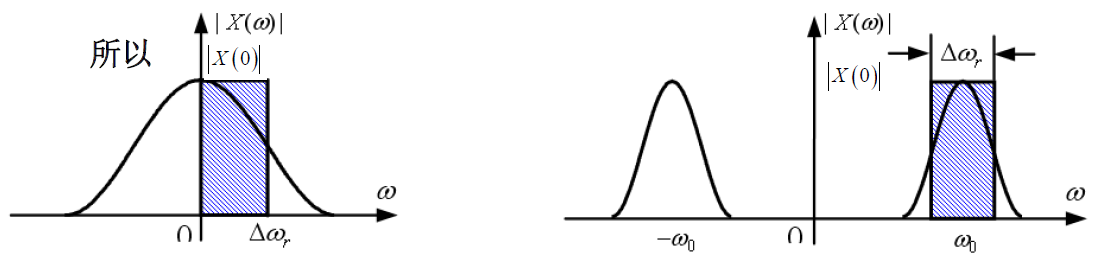
随机信号带宽

• 随机信号不满足绝对可积，不存在频谱，只能用功率谱描述随机信号在频域的特点
• 利用白噪声通过系统后的功率谱来定义的，实质上是把一个系统的功率传输函数等效成理想系统的功率传输函数
• 等效原则：
  • 保持信号的选择性不变
  • 等效前后的面积不变（输出功率不变）
  • 等效后矩形的高度为其最大值
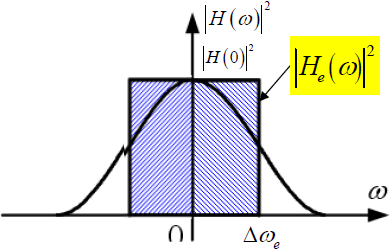
• 等效带宽，等效后矩形正频率部分的宽度即为等效噪声带宽
• 低通信号：
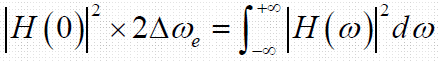
• 带通信号：

• 由单边和双边功率谱密度定义的等效噪声带宽是相同的

  4.1.3 随机过程带宽

• 低通过程：

• 带通过程：

  4.1.4 随机过程的均方带宽

  （归一化功率谱密度的标准差）

• 低通过程：

• 带通过程：
• 是方差（标准差）概念的等效
• 归一化方法采用平均功率归一化，与用最大值归一化方法不同

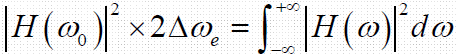
4.2 白噪声通过理想线性系统

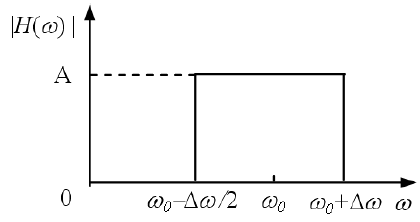
4.2.1 理想低通系统

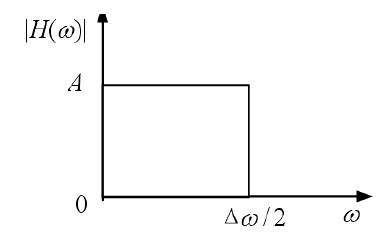
• 白噪声过程的单边功率谱密度：
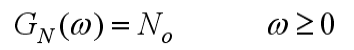
• 白噪声通过理想低通系统后输出随机过程的单边功率谱密度：

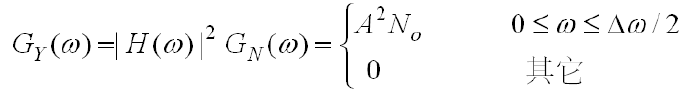
• 系统输出的自相关函数：

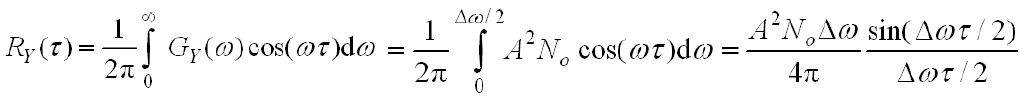
• 可计算平均功率：

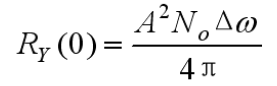
• 相关系数（白噪声的数学期望为0）：

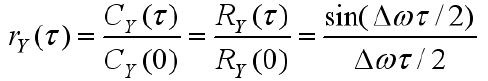
• 相关时间：

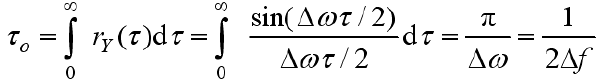
• 结论：白噪声通过理想低通系统后

  • 功率谱宽度变窄，无限宽到
  • 平均功率由无限变为有限，与系统带宽成正比
  • 相关性由不相关变为相关，相关时间与系统带宽成反比，满足时间带宽积一定
  • 输入白噪声是剧烈变化的，通过低通系统后起伏变得缓慢

    4.2.2 理想带通系统

    

• 白噪声过程的单边功率谱密度：

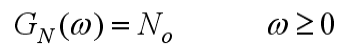
• 白噪声通过理想低通系统后输出随机过程的单边功率谱密度：

• 系统输出的自相关函数：

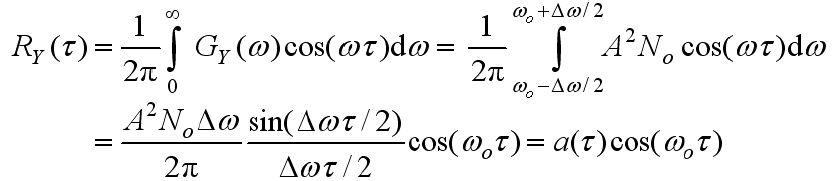
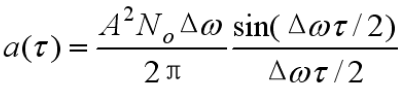
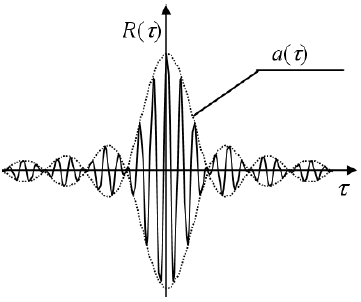
的表达式与低通系统的自相关函数一样，相差2倍是因为带通系统带宽比低通系统大一倍
为自相关函数的包络，为载波部分，当时，带通系统退化为低通系统

• 可计算平均功率：

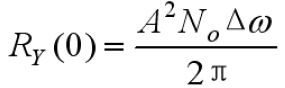
• 相关系数（白噪声的数学期望为0）：

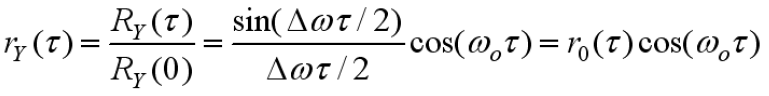
• 相关时间（不考虑载频）：

4.3 白噪声通过实际线性系统

• 线性系统为单边高斯带通系统

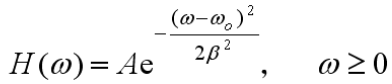
• 白噪声过程的单边功率谱密度：

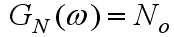
• 白噪声通过高斯带通系统后输出随机过程的单边功率谱密度：

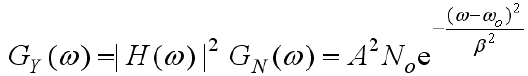
• 系统输出的自相关函数：

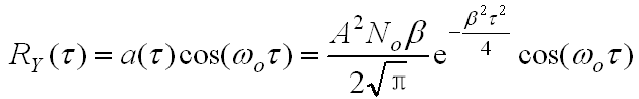
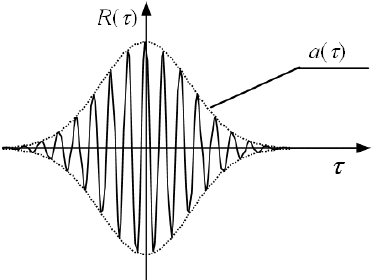
• 系统输出的自相关函数的包络：

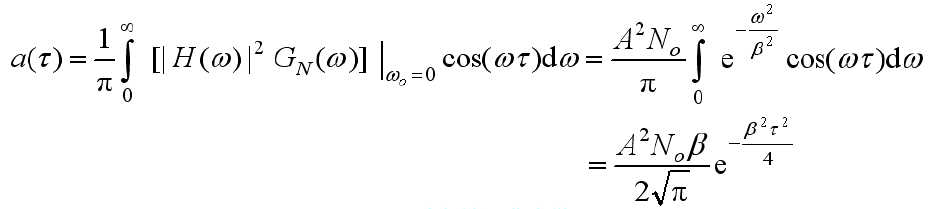
• 输出的平均功率：

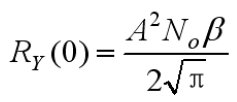
• 相关系数：

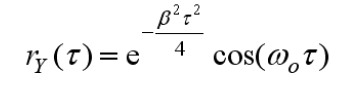
• 等效噪声带宽：

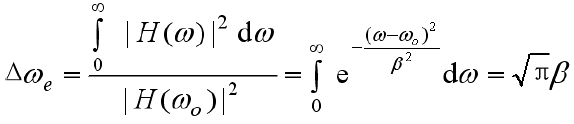
• 相关时间：