简介

遗传算法（Genetic Algorithm, GA）来源于进化论和群体遗传学，由美国的 Holland 教授于 1975 年在他的专著《自然界和人工系统的适应性》中首先提出。
遗传算法作为一种非确定性的拟自然算法，为复杂系统的优化提供了一种新思路，对于诸多NP-Hard问题，遗传算法都有不错的表现。
相对于传统算法而言，遗传算法有以下突出优点：

  1. 可适用于灰箱甚至黑箱问题；
  2. 搜索从群体出发，具有潜在的并行性；
  3. 搜索使用评价函数（适应度函数）启发，过程简单；
  4. 收敛性较强。
  5. 具有可扩展性，容易与其他算法（粒子群、模拟退火等）结合。

遗传算法有以下不足：

  1. 算法参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验；
  2. 遗传算法的本质是随机性搜索，不能保证所得解为全局最优解；
  3. 遗传算法常见的编码方法有二进制编码、Gray编码等。
    1. 二进制编码比较常见，但是二进制编码容易产生汉明距离（Hamming Distance）（将一个字符串变换成另外一个字符串所需要替换的字符个数）
    2. 可能会产生汉明悬崖(Hamming Cliff）（相邻整数的二进制编码之间存在汉明距离，交叉和遗传难以跨越）
    3. Gray可以克服汉明悬崖的问题，但是往往由于实际问题的复杂度过大导致Gray编码难以精确地描述问题。
  4. 在处理具有多个最优解的多峰问题时容易陷入局部最小值而停止搜索，造成早熟问题，无法达到全局最优。

    算法的发展与重心

    经过多年的发展，遗传算法的研究热点及发展方向：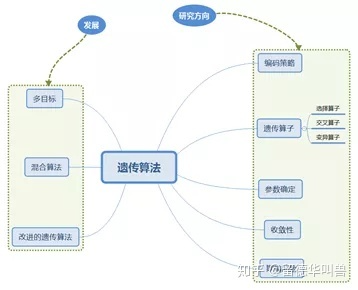
    image.png
    遗传算法的搜索核心是遗传算子的选择，因此对于遗传算法的研究，其中最常见的内容与方向是遗传算子，遗传算子的选择多样性也导致了算法表现的多样性，常见的选择方式如图所示：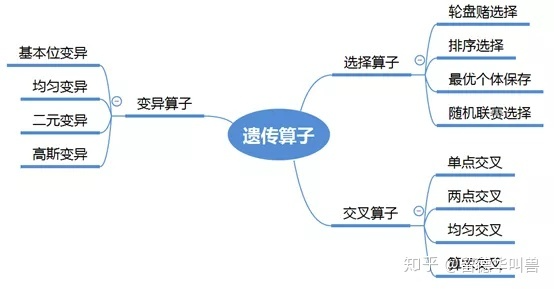
    image.png

    实例说明

    为了更通俗地理解遗传算法，下面将通过一些实例进行描述：

如果想在一座连绵的大山上找到其最高点，正常情况下你需要爬遍整座山才可以找到最高峰，但大多数的智能算法并不需要搜索整个山峰，不同的智能算法有不同的求解思路，举几个简单例子：

  1. 爬山算法（也称为贪心算法）。假设有一只猴子从山的任意一点出发，当它爬到第一个高峰值点的时候便停止前进，并认为当前的山峰为整座山最高的点。这种情况下，运气好可能会到达最高点，但是大概率情况下都不会是最高点。

  2. 模拟退火算法。假设有一只神志不清的猴子，当它爬到山峰的时候，它有一定的概率继续出发，也有概率停止前进。这种情况下它也有可能通过有限的时间找到整座山的最高点。

  3. 遗传算法。假设山上有一群猴子，猴子生存的食物只有在山峰处才有，而且山峰越高食物量越充裕。那么这些猴子为了生存，会不断聚集在各个山头上进行生存繁衍，而这些山峰可以理解为各种局部最优解（图3中类似绿色和蓝色的地方），如果种群规模足够大，势必会有一群猴子聚集在了整座山的最高点，也就是全局最优解（图3中红色位置）。

基于以上三种算法的描述，我们可以对智能算法有一个简单的了解：无论是哪种算法，都具有一定的随机性，都不能保证最终选择的山峰为整座山的最高点。但是在实际生活中，有诸多类似的问题，如果要考虑所有的情况可能会花费大量的时间，而恰巧我们并不需要一个最好的结果，我们只需要快速找到一个相对较好的结果便可以满足要求的时候，智能算法的意义便得到了体现。

背包问题模型

问题描述：假设一个你有一个可以装五公斤重的背包，现在地上有三块重金属A、B、C供你挑选，重量分别为1公斤、2公斤、3公斤，价值分别为1万元、5万元、10万元。为了使得总体收益最大，应该选择哪些金属块装入背包。

问题分析：这种规模的问题我们可以直观看出最优解为，选择B、C带走可以获得最大收益。但当问题规模扩大十倍百倍的时候，我们就必须要借助计算机来进行求解了。

下面分别以三种算法为例进行说明：

  1. 爬山算法：

初始点不确定，背包放不下就放手。

假设第一步选择A金属，有如下情况：A→B→C（保留AB），A→C→B（保留AC）；假设第一步选择B金属，有如下情况：B→A→C（保留BA），B→C→A（保留BC）；假设第一步选择C金属，有如下情况：C→A→B（保留CA），C→B→A（保留CB）；

可以看出，一共六种情况下，只有两种情况（选择BC）是可以得到最好结果的。侧面说明了爬山算法具有很大的不确定性。

  1. 模拟退火算法：

模拟退火与爬山最大的不同就是，每次拿到金属块的时候我们有一定的概率来决定是否将这块金属放入背包。我们假设这个概率为0.5（几乎所有的智能算法都需要提前设定初始参数，而不同的初始参数对求解结果及求解效率的影响非常大。）每次拿到金属块都有0.5的概率保留或者选择下一块，当执行足够多的次数后总能得到结果，结果虽然不一定是最好的，但整体随机性更大，当问题规模较大的时候更有可能选出最优解。

  1. 种群遗传算法：

初始随机产生100个15位2进制变量（每3位分别对应A、B、C，0为不取，1为取）
其中111为不可能的情况，设定这种基因片段不能繁衍下一代。

image.png

总生存力为五个基因片段之和，设定第一个位置出现1则生存力加0.01，第二个位置出现1则生存力加0.05，第三个位置出现1则生存力加0.1。
则a为0
b1、b2和b3分别为0.1、0.05和0.01
c1、c2和c3分别为0.06、0.11和0.15

生存力越高则生存率越高，依据轮盘赌选择策略（生成随机数，落在生存率区间选择相应的个体），选择遗传下一代的个体。

生存率=个体生存力/总生存力。

选择方法：

随机生成6个0-1的数，根据落在哪里选对应的个体。

表1表2分别表示了种群的选择和遗传。

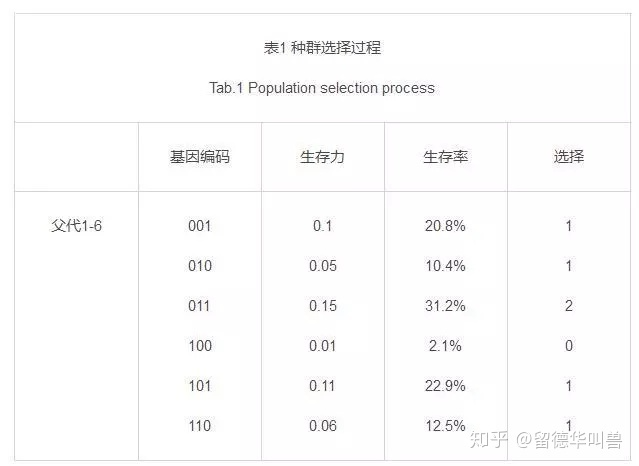
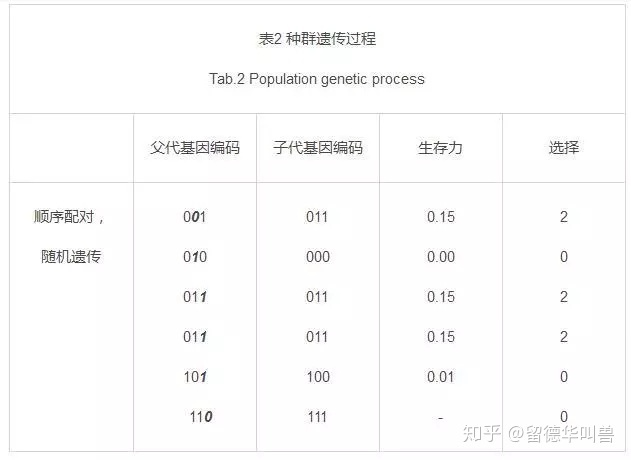
image.png
image.png
由于问题简单，规模较小，一次遗传之后便可以得出很明显的结果：
种群中留有大量的011基因，即选择BC的结果。
但是当问题规模扩大十倍百倍的时候往往需要多次迭代才会有明显的区分度。

另一方面，如果种群陷入了100与100的配对循环，那么这种情况下，永远不可能得出最好的情况011
这个时候需要对基因的某一段进行变异，将100变异为101或110，种群就会出现更优的基因型。
但是在实际问题中变异不一定是向好的方向发展，也有可能会出现更坏的结果。

总的来说，遗传算法的选择充满了不确定性。
但是当你设定无穷大的种群规模，足够长的繁衍时间后，最终总会达到最优，但是时间也会成倍上升。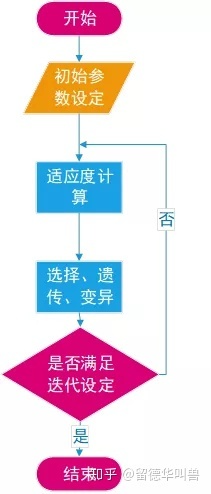
image.png
适应度的概念在遗传算法中表示为个体趋近于最优解的程度，适应度越高遗传到下一代的概率就越大。
上述的例子中，我们自己选择了适应度函数（生存力），在日常建模的时候，生存力函数可以是目标函数，也可以自己选择。
在演化计算中
某些特殊算子的选择方式（例如这里的轮盘赌选择）要注意两点：

  1. 适应度必须非负
  2. 优化过程中目标函数的变化方向应与群体进化过程中适应度函数变化方向一致

但在诸多大规模非凸非线性问题的求解时，上述观点不再适用。