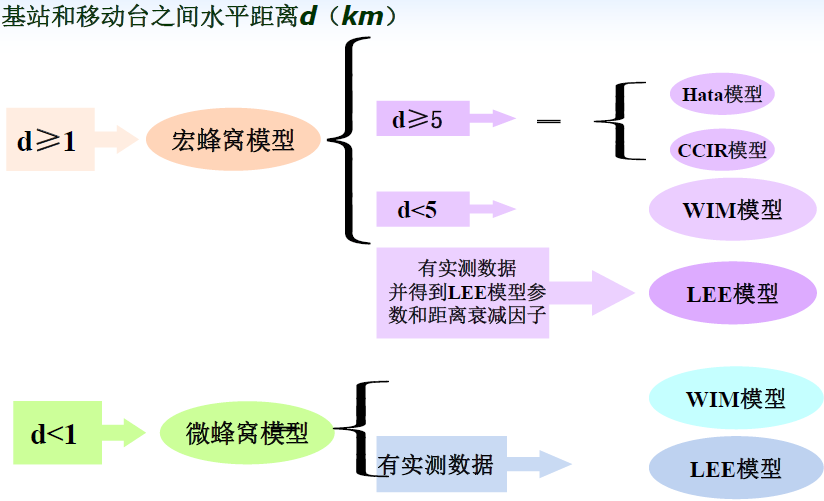
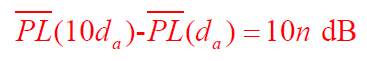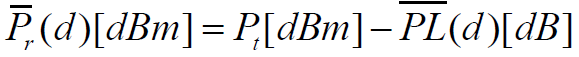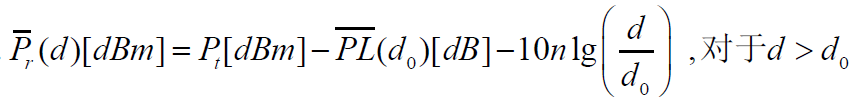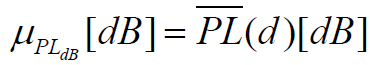6. 电波传播损耗预测模型
- 目的:
- 掌握基站周围所有地点处接收信号的平均强度及变化特点,为网络覆盖的研究以及整个网络设计提供基础
- 方法:
- 根据测试数分析归纳出基于不同环境的经验模型,在此基础上对模型进行校正,使其更加接近实际准确
- 因素:
- 地形/建筑/植被/天气/噪声/运动
- 内容
- 室外传播模型
- 室内传播模型
- 传播模型校正
6.1 路径损耗模型
- 理论+实测
- 路径损耗指数n,常用n=4
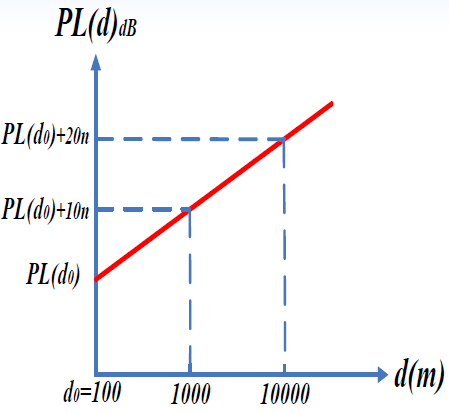
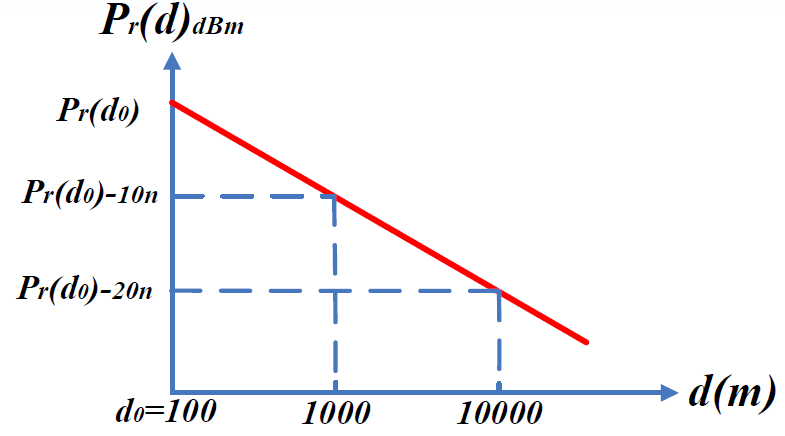
- 平均路径损耗
随距离
的变化规律为:

- d0为靠近发端的参考点距发端的距离。该参考点处的路径损耗一般可以通过实测获得。n为路径损耗指数,具体取值依赖于传播环境。
- 公式中的上划线表示给定距离d的所有可能的路径损耗值的整体平均。
- 参考点也应位于发射天线的远场。
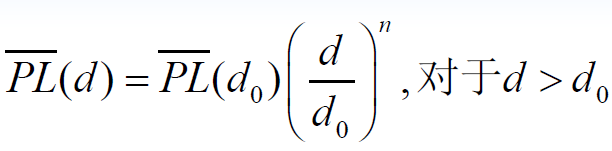
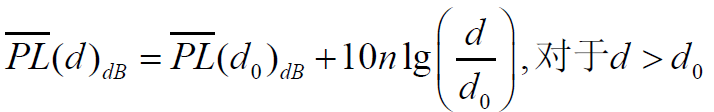
- 表明平均路径损耗的分贝值(dB)按每十倍距离增加10n dB的规律线性递增。
- 如对于任意da>d0,有:
6.2 对数距离路径损耗模型
- 以平均接收功率表示
6.3 阴影衰落
- 大尺度衰落
- 信号在无线道传播过程中遇到的障碍物会使发生随机变化,从而造成给定距离处接收信号功率的随机变化
- 反射面和散体的变化也会造成接收功率随机变化
- 造成信号随机衰减的因素,包括障碍物位置、大小和介电特性及反射面和散体的变化情况等, 这些因素一般 都是未知的 ,因此只能用统计模型来表征这种随机衰减。
-
6.4 对数正态阴影模型
给定距离处,实际的路径损耗呈现出随机变化,其分贝值的概率密度函数
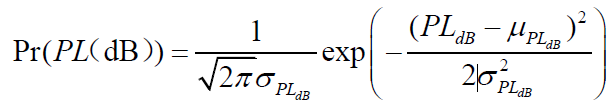
- 其中,
是对数距离路径损耗模型中所得到的给定距离处的平均路径损耗的分贝值
为标准差
这两个参数都是以dB计
一个随机变量的分贝值服从正态分布,则该随机变量服从对数正态分布
- 概率密度函数的表达式可以导出
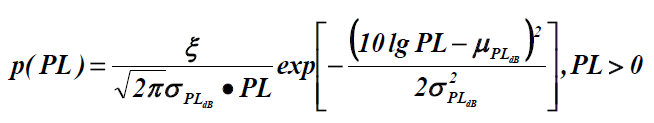
给定距离处的路径损耗分贝值
服从正态分布,则
将服从对数正态分布
另一种形式
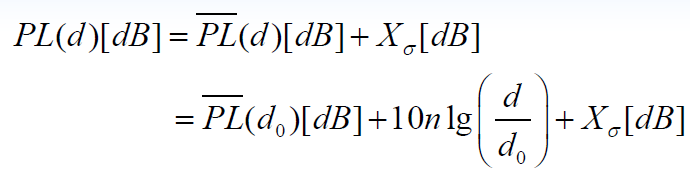
是均值为0dB,标准差为
dB的正态随机变量
- 实际上
6.5 Q函数
- 对于标准正态随机变量X
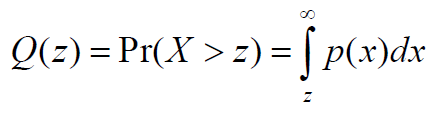
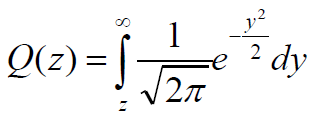

- 函数性质
6.4 中断概率
- 在给定距离上,接收功率小于系统最小可用功率的概率,称为中断概率
- 根据上述模型,我们知道给定距离上的接收功率为
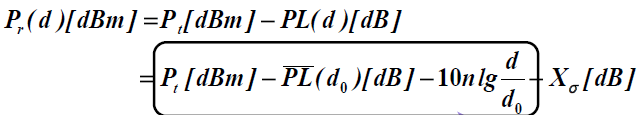
- 圈住部分为平均接收功率
- 接收功率(以dBm计的)也服从正态分布
- 设接收信号功率门限为γ,则接收信号功率的累积分布函数(CDF)可表示为
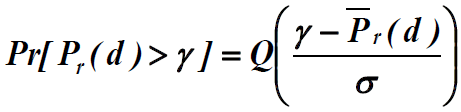
- 接收功率低于门限γ的概率为
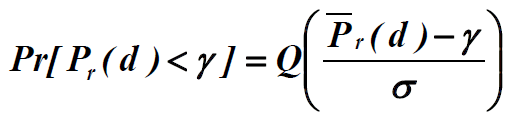
- 所以中断概率为
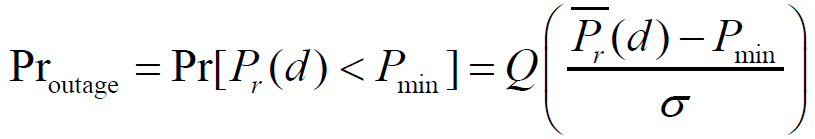
- 例题
6.5 小区覆盖范围
- 设基站位于小区中心,并采用全向天线,小区覆盖范围则为小区内所有位置之中
- 接收功率超过最小可用接收功率的位置所占的百分比
-
6.6 小区边缘覆盖率
设基站位于小区中心,并采用全向天线
- 如果小区范围内不存在阻挡物,则覆盖边缘近似为圆周——不存在阴影衰落
- 存在阻挡物引起阴影衰落
- 如果以接收机实时接收功率,达到最小可用接收电平作为形成小区边缘的实际标准的话
- 等接收功率线将不规则
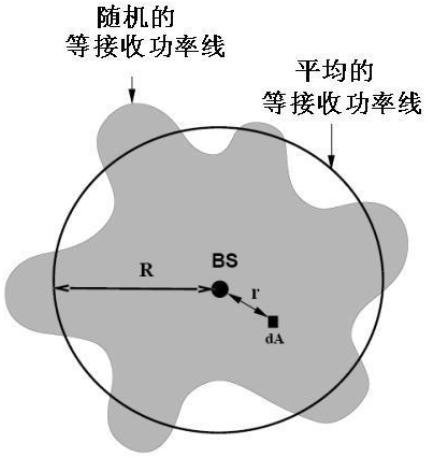
- 定义概率
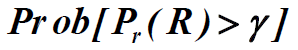
- 为小区的边缘覆盖概率
- 表示在我们设想的小区边界上(半径为R的圆周)上实际接收功率(不是平均接收功率)大于最小可用接收功率
的概率
- 根据对数正态阴影模型
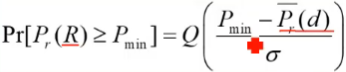
- 如果使得半径为R的圆周上的平均接收功率恰好等于接收机的最小可用接收功率γ的话,小区的边缘覆盖率就等于50%
6.7 覆盖范围与边缘覆盖率关系
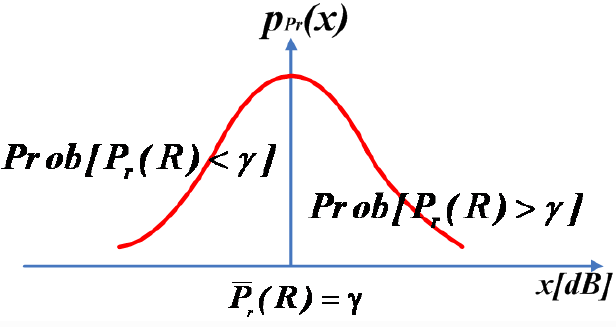
- 小区覆盖范围(即小区的面积覆盖率)是从覆盖面的角度来衡量
- 而小区的边缘覆盖率从线的角度
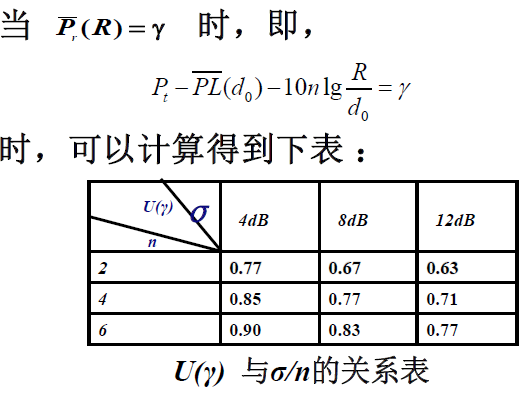
- 说明
的含义
- 在我们设想的小区边界(半径为R的圆周)上的平均接收功率等于系统最小可用接收功率(
)
- 由于以dBm计的接收功率服从正态分布
- 所以这个条件意味着在边界上接收功率
为
- 在我们设想的小区边界(半径为R的圆周)上的平均接收功率等于系统最小可用接收功率(
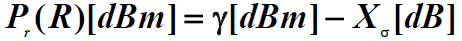
- 即在设想的小区边界上接收信号功率大于
的概率为
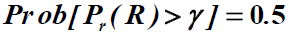
- 因为
就是随机变量
的均值
- 这样边缘覆盖概率为0.5,任何时刻边界上所有点中仅50%的位置其接收功率能够超过最小可用接收功率
- 表格数据含义
- 如
- 意为当边界覆盖率达到50%时,
的情况下,小区的覆盖率可以达到77%
- 给定n时,小区覆盖范围随σ减小而增大
- 这是因为σ较小说明接收信号在平均接收功率附近变化的范围较小。
- 根据前面的分析,存在阴影衰落情况下,在小区边界处使平均接收功率达到最小可用接收功率只能提供 50 %的边缘覆盖率, 而在 σ/n =2dB 的情况下,小区覆盖范围也只能达到77 %
- 实际所需的小区的边缘覆盖率(线覆盖率)应该要达到90 %以上
此时,小区覆盖范围(面积覆盖率)将会更高,如可能达到99 %
当边缘覆盖率(线覆盖率)达到90 %
- 即保证
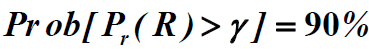
- 根据对数正态阴影模型
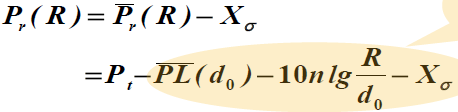
- 标注部分与传播环境有关
- 只有Pt是不受传播环境约束,可以调整的量
所以要提高线覆盖率的最直接措施就是增大基站发射功率
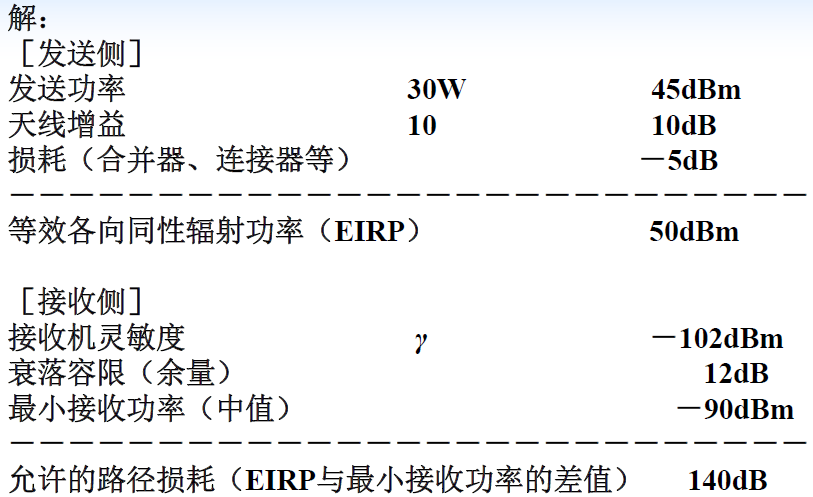
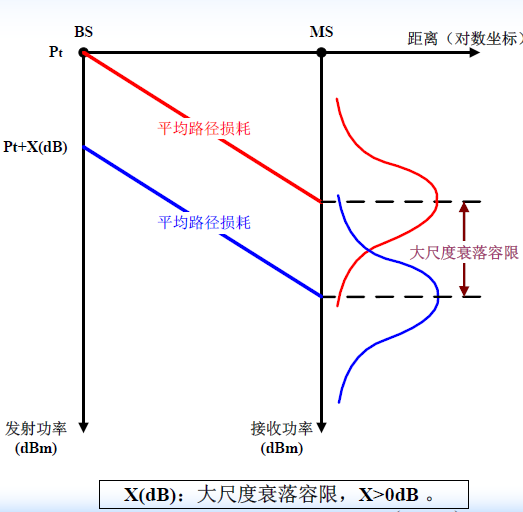
衰落容限定义
- 我们将保证给定边界 (如半径等于R的圆周)上的覆盖率达到比较高的程度所需要增加的发射功率分贝 (dB )值称作衰落容限,即大尺度衰落容限
- 或者,在基站发射功率有所增加(以保证适当的边缘覆盖率)时,衰落容限表示界处的接收功率平均值(或中)应当比系统最小可用功率大出来的分贝值
- 例题
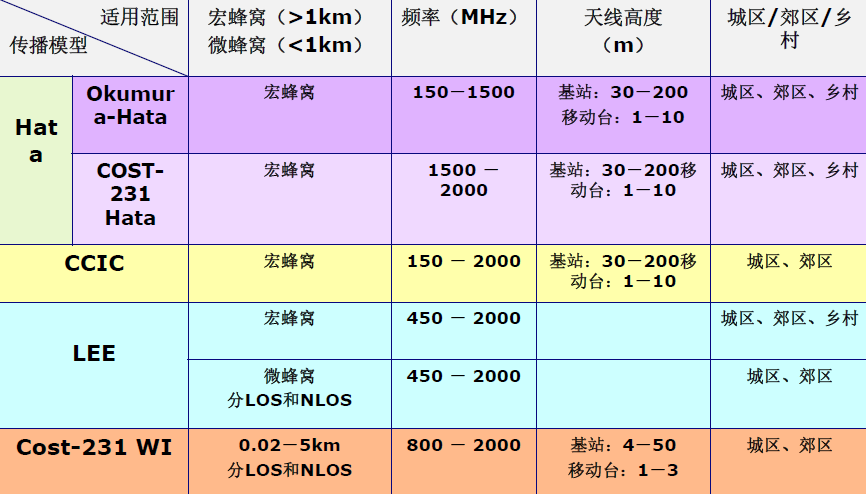
7.室外传播模型
7.1 Okumura-Hata模型
- 即奥村模型
- 大量测量得到,对蜂窝系统链路预测时使用最多的大尺度预测模型
- 预测基站到移动台(前向链路)的路径损耗中值
- 概率中值
- 某随机变量X,设a是其取值范围内的一个数值,如果该数值满足:
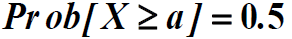
- 就称a为X的中值
- 对于正态分布,中值就是均值
- 但对于其他的概率分布,中值未必等于均值
- 在不能确知概率分布的情况下,一般采用概率中值作为统计分析的结果