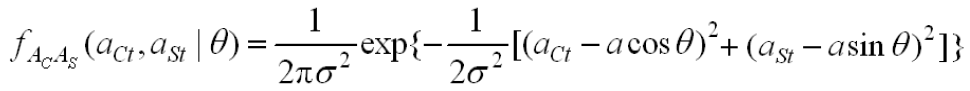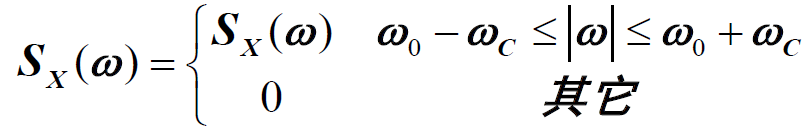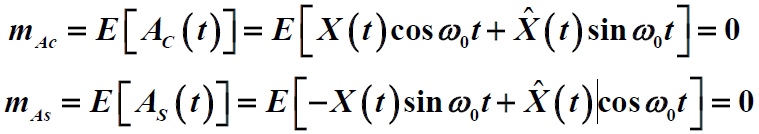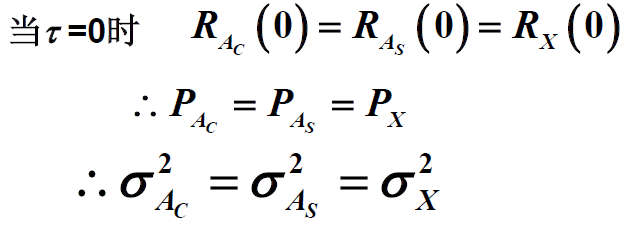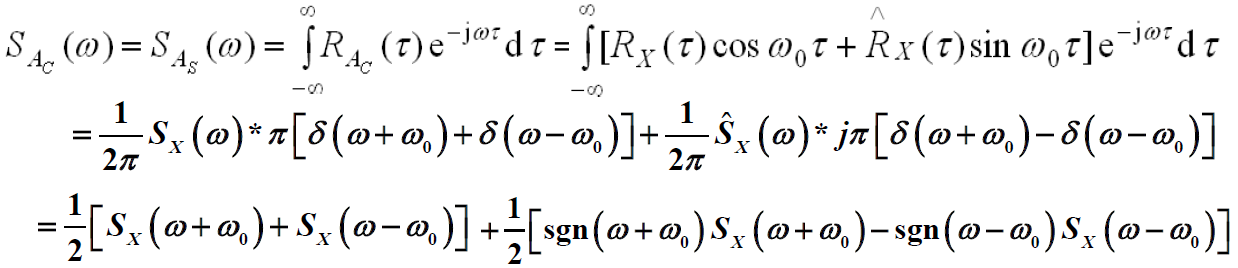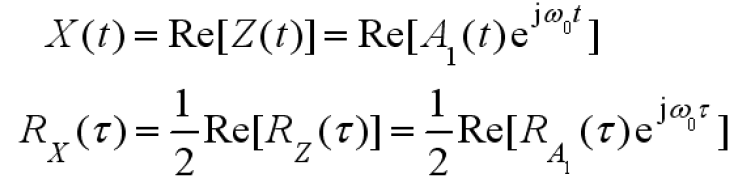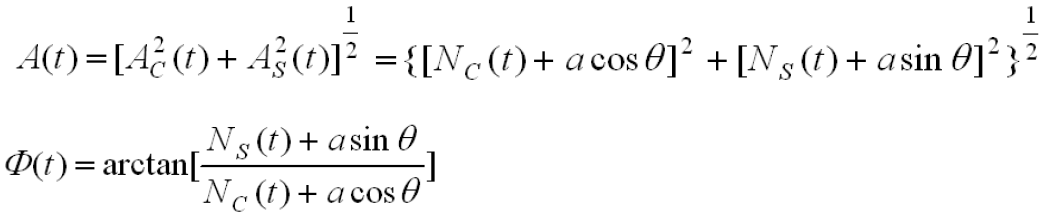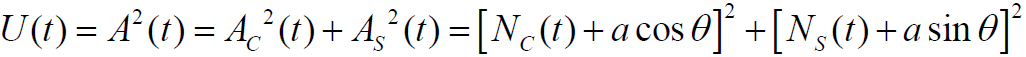• 窄带随机过程定义：一个实平稳随机过程X(t)，若它的 功率谱 密度满足

而且带宽满足，则称此随机过程为窄带平稳随机过程

1. 窄带随机过程的表示方法

1.1 准正弦振荡表示

• 任何一个实平稳窄带随机过程X(t)都可以表示为

1.2 正交表示（莱斯表示）

• 为窄带滤波器的中心频率，是另外两个随机过程
• 满足

2. 窄带随机过程的特点

• 设X(t)是任意的宽平稳、数学期望为0的是窄带随机过程

• 用及希尔伯特变换表示两个正交分量

• Ac(t)和As(t)可看作是X(t) 线性变换的结果
• 由是宽平稳随机过程，所以也是宽平稳随机过程

  2.1 正交分量的统计特性

  数学期望
  
  自相关函数
  
  
  
  
  
  平均功率
  
  功率谱密度
  
  可通过画图求解得

若关于±对称

互相关函数

**

• 由于
• 和的互相关函数是奇函数
• 即有
• 和在同一时刻的状态是正交的随机变量

互功率谱密度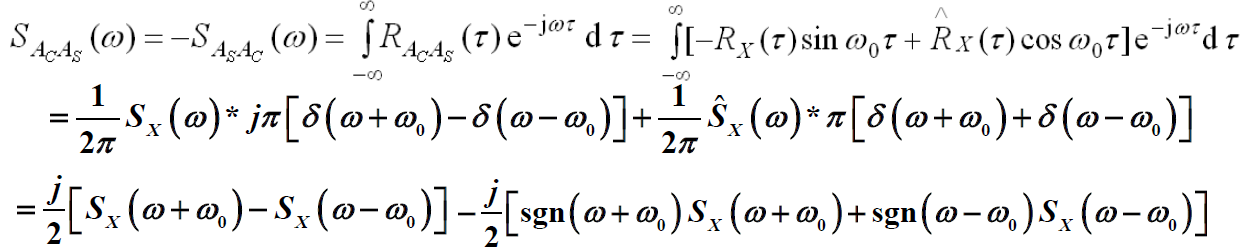

可通过画图求解得

如果窄带过程的单边功率谱是关于偶对称的

2.2 窄带随机过程分析结论

2.3 窄带过程的解析表示

• 设X(t)是数学期望为0的宽平稳、实窄带随机过程
• 构成解析随机过程Z(t)

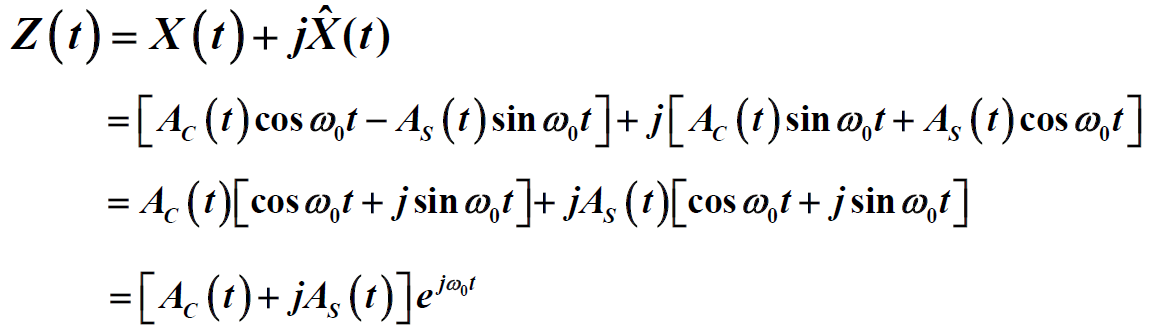
令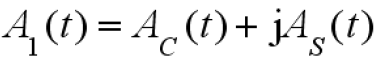

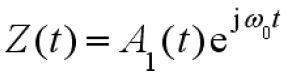
• 为低频复随机过程
  • 的数学期望

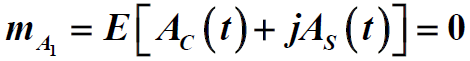
• 的自相关函数

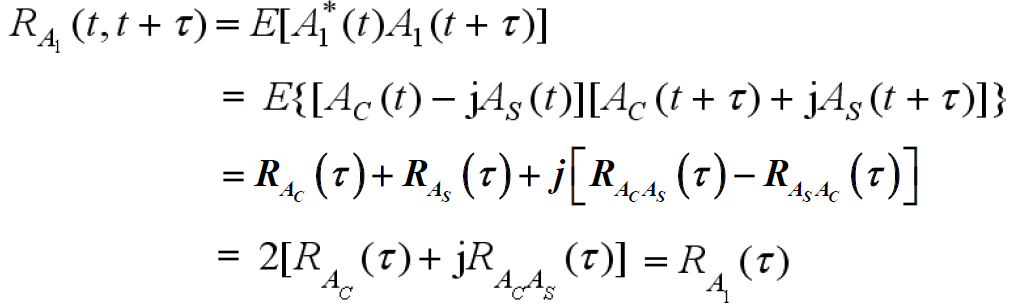
• 可知为一复平稳随机过程
  • 的自相关函数

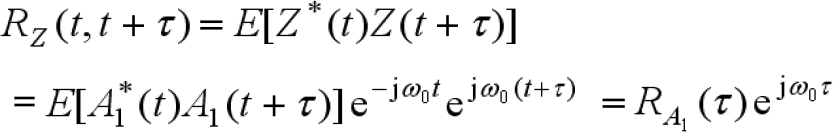
• 综上

3. 窄带高斯过程

3.1 包络和相位的一维分布

• 设X(t)是窄带平稳高斯随机过程，其数学期望为0，方差为σ2

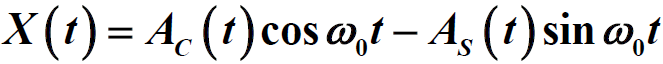
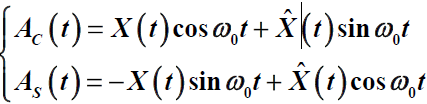
• 和也是数学期望为0，方差为σ2的高斯过程
• 和任意相同时刻都是正交的，它们任意相同时刻也是统计独立和不相关的（高斯随机变量三等价）

• 

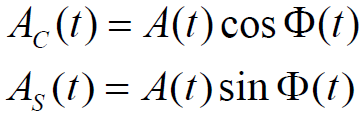
• 包络和相位分布的求解过程

  • 正交分量和同相分量的联合分布（和都是高斯分布，且相互独立）
  • 二维随机变量变换，利用雅可比变换求得包络与相位的联合分布
  • 用PDF降维性求包络与相位的一维分布

• 结论

  • 窄带高斯过程的包络服从瑞利分布
  • 窄带高斯过程的相位服从均匀分布
  • 窄带高斯过程的包络和相位在 同一时刻 是相互独立的随机变量

    3.2 包络和相位的二维分布

• 单边功率谱密度，以为对称的窄带平稳高斯随机过程，数学期望为0，方差为

• 包络和相位分布的求解过程
  • 确定正交分量和同相分量的联合分布（四维）
  • 利用已知的和的四维概率分布来求包络和相位的四维概率分布
  • 利用PDF降维性求包络与相位的二维分布

• 结论

  • 窄带高斯过程的包络和相位不是两个统计独立的随机变量

    3.3 包络平方的分布

• 窄带高斯过程通过平方律检波器，可得到包络的平方，即平方律检波器的输出为

• 包络平方分布的求解过程
  • 函数变换法

• 结论

  • 窄带高斯过程的包络平方服从指数分布

    3.4 结论

    

    4. 窄带随机过程加余弦信号

• 系统模型

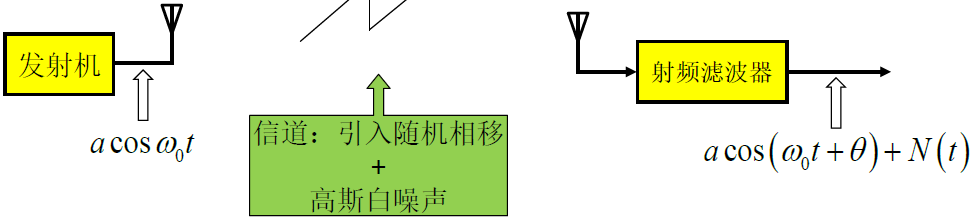
• 令

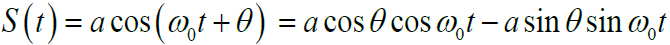
为在上均匀分布的随机变量，为常数振幅

• 噪声为数学期望为0，方差的窄带高斯过程

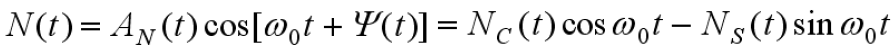
• 信号合成

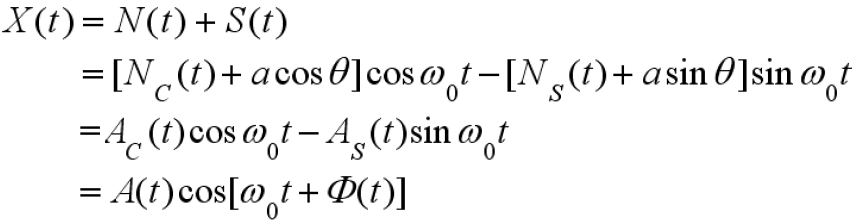
• 也是随机窄带信号
• 此时同向分量和正交分量为

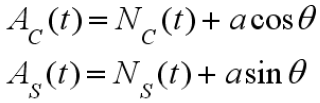
• 合成信号的包络和相位为

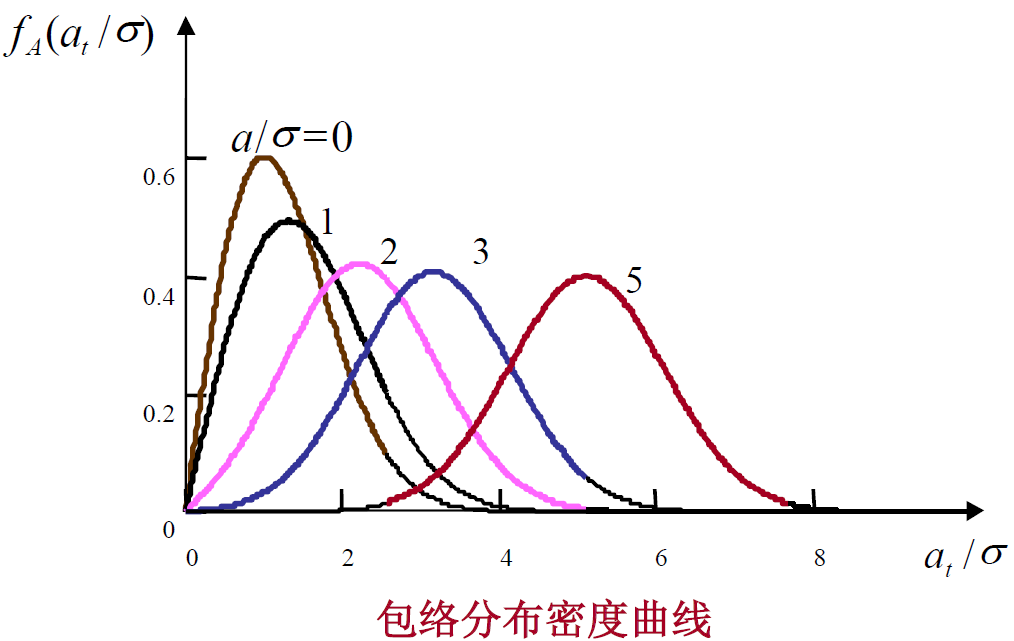
4.1 合成信号包络和相位分析

• 由于

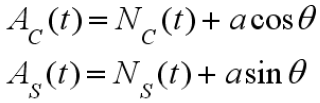
给定，任意时刻，和也是互相独立的高斯变量

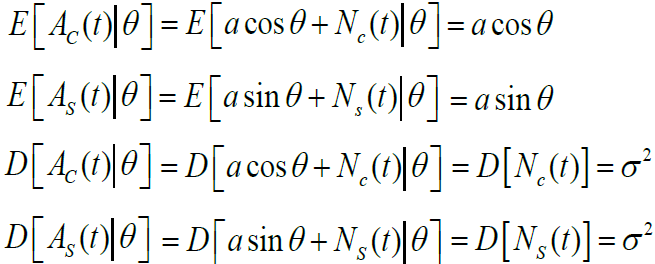
给定，和的联合概率密度（满足高斯分布）

• 合成信号的包络和相位概率分布的求解过程

  • 同相分量和正交分量的联合概率分布
  • 函数变换得到包络和相位的联合概率分布
  • 降维得到包络的条件概率分布和相位的条件概率分布
  • 通过，
  • 得到联合概率分布，
  • 降维得到包络的概率分布和相位的概率分布

• 结论

  • 合成信号的包络服从的莱斯分布
  • 当信噪比很小时，即时，趋近于瑞利分布，信噪比为0时，莱斯分布就是瑞利分布
  • 当信噪比很大时，即时，趋近于高斯分布
  • 
  • 当信噪比很小时，相位趋近于均匀分布
  • 当信噪比很大时，相位趋近于高斯分布

    4.2 合成信号包络平方的概率分布

    

• 结论

  • 合成信号包络平方服从的非中心卡方分布