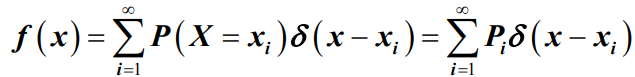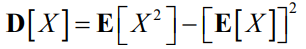- 通信网规划设计和优化遵循的原则:
- 能够满足各项性能指标要求又节省费用的设计或优化方案。
- 对设计人员的要求:
- 掌握相应的理论基础知识和网络分析的计算方法,以便对通信网的性能进行分析与指标计算,为设计和优化提供理论数据
- 数学理论:排队论。
- 它起源于最早的电话系统,可应用于很多领域,,目前通信网仍是其中一个重要的应用领域。
- 重点掌握和理解排队论的基本概念、M/M/m(n)排队系统的模型分析方法,了解它们在网络中的实际应用;
- 掌握通信网业务量的基本概念,理解、掌握和运用Erlang B公式和Erlang C公式;能够运用这些知识分析和计算实际网络的性能指标;
- 掌握随机接入系统的工作原理及其业务分析方法。
参考书籍
- 陆传赉.《排队论(第2版)》,北邮出版社;
- 盛友招.《排队论及其在现代通信中的应用》.人民邮电出版社
- Donald Gross .《Fundamentals of Queueing Theory(4th edition)》. John Wiley & Sons ;
- 天津大学管理学院运筹学课程:排队论
- http://course.tju.edu.cn/tddg/postgraduate/ppt/indexG.html
5.1排队论概念
排队论(Queuing Theory) :
- 是一个独立的数学分支,有时把它归到运筹学中
- 是专门研究由于随机因素的影响而产生的拥挤现象(排队、等待)的科学,也称为随机服务系统理论或拥塞理论(Congestion Theory)
- 是在研究各种排队系统概率规律性的基础上,解决有关排队系统的最优设计和最优控制问题。
- 排队论的起源:
- 排队论起源于20世纪初。当时,美国贝尔(Bel) 电话公司发明了自动电话以后,如何合理配置电话线路的数量,以尽可能地减少用户重复呼叫次数问题出现了。
- 1909年,丹麦工程师爱尔兰(A.K.Erlang) 发表了具有重要历史地位的论文,从而在理论上求解了.上述问题《The Theory of Probabilities and Telephone Conversations》。
- 1917年,爱尔兰又提出了有关通信业务的拥塞理论,用统计平衡概念分析了通信业务量问题,形成了概率论的一个新分支。《Solution of Some Problems in The Theory of Probabilities of Significance in Automatic Telephone Exchanges》
- 后经C.Palm等人的发展总结,由近代概率论观点出发进行研究,奠定了话务量理论的数学基础。《Methods of Judging The Annoyance Caused by Congestion》
- 经过通信、计算机和应用数学三个领域的研究学者的努力,排队论得到了迅速的发展和应用。
- 应用:
- 网络的设计和优化方法;
- 移动通信系统中的切换呼叫的处理方法;
- 随机接入系统的流量分析方法;
- ATM业务流的数学模型及其排队分析方法等。
经典排队论
随机变量可以分为离散型和连续性两大类。
- 为了描述随机变量各可能取值与相应概率之间的对应关系,一般用 分布律来研究随机变量的统计规律。
- 定义:随机变量X取值不超过x的概率称为概率分布函数
- 其中,P(X≤x)表示随机变量X小于等于某个可能取值x的概率。概率分布函数Fx(x)有时也称为累积分布函数(CDF, Cumulative Distribution Function) 或积分分布函数。
- 根据概率分布函数的定义,可得到如下性质:
- 性质1 Fx(x)是x的单调非递减函数,当
时有
- 性质2 Fx(x)非负,且取值满足
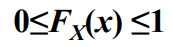
- 性质3 随机变量在x到x,区间内的概率为
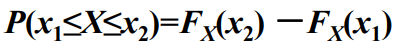
- 性质4 Fx(x)右连续,即
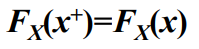
- 定义:连续性随机变量的概率分布函数的导数为概率密度函数

- 概率密度的积分形式就是概率分布函数:
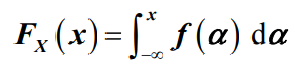
- 性质1 概率密度函数非负
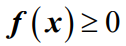
- 性质2 概率密度函数在整个取值区间积分为1
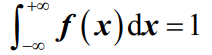
- 性质3 概率密度函数在x1到x2区间内积分是该区间的取值概率
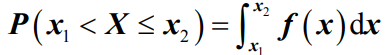
- 定义:离散型随机变量,其概率密度定义为
5.2.2随机变量的数字特征
- 数学期望
- 数学期望描述了随机变量的集中特性,有时候也称为统计平均、集合平均或均值
- 连续性随机变量数学期望

- 离散型随机变量的数学期望为
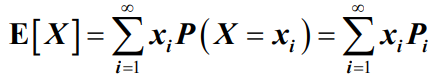
- 其中,Pi是随机变量X所取数值xi的相应概率
- 方差
- 方差用来度量随机变量偏离数学期望的程度,也就是随机变量在数学期望附近的离散程度。
- 连续性随机变量的方差
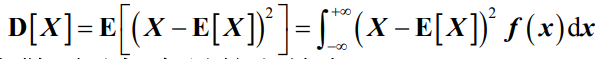
- 离散型随机变量的方差为
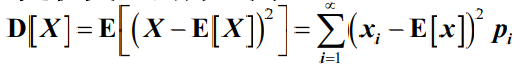
- 方差开放后就是均方差或标准差
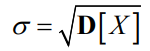
- 离散型随机变量和连续型随机变量的方差计算经常用到简化公式
5.2.3常用概率公式
- 1.全概率公式
- 设
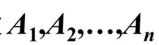 是互不相容的事件,且
是互不相容的事件,且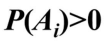 ,若对任意事件B,有
,若对任意事件B,有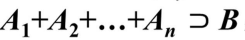 ,则有
,则有
- 设
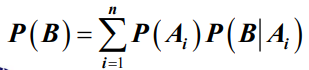
- 2.贝叶斯公式
- 设
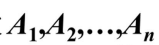 是互不相容的事件,且
是互不相容的事件,且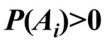 (i=1,2…,n),若对任意事件B ,有
(i=1,2…,n),若对任意事件B ,有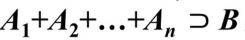 ,且P(B)>0,则有
,且P(B)>0,则有
- 设
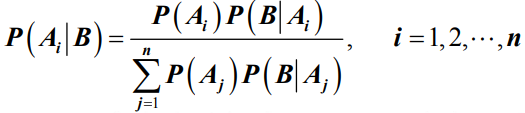
- 其中,P(Ai)称为先验概率, P(Ai|B)称为后验概率
- 3.乘法定理
- 设A、B是任意两个事件,则有:
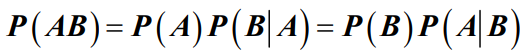
- 4. 事件独立性
- 设A、B是任意两个事件,如果有
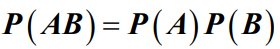
- 则称A与B是相互独立的。如果P(A)>0 ,则有
5.2.4常用概率分布
- 确定性分布
- 设离散型随机变量X以概率为1取常值a,即
- 确定性分布

- 则称随机变量X服从确定性分布。它的概率分布函数为
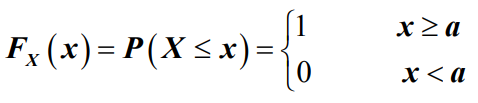
- 泊松分布
- 泊松分布常用来描述顾客到达间隔分布。设离散型随机变量X所有可能的取值的概率为:
- 泊松分布
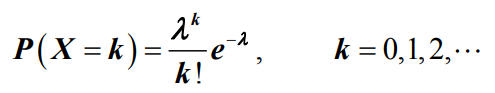
- 其中,λ(>0)为常数,则称随机变量X服从参数为λ的泊松分布。
- 随机变量X的均值为:E[X]=λ
- 随机变量X的方差为:D[X]=λ
- 负指数分布
- 负指数分布常用来描述排队系统中服务时间分布,设连续型随机变量 X具有概率密度函数为:
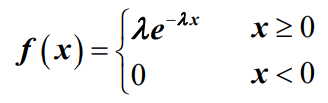
- 其中,λ(>0)为常数,则称随机变量X服从参数为λ的负指数分布,简称指数分布。其分布函数FX(x)为:
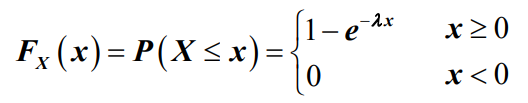
- 随机变量X的均值为

- 随机变量X的方差为

- 负指数分布有一个重要的性质是“无记忆性”或“无后效性”,即
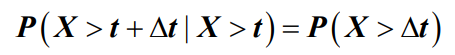
- 这是因为
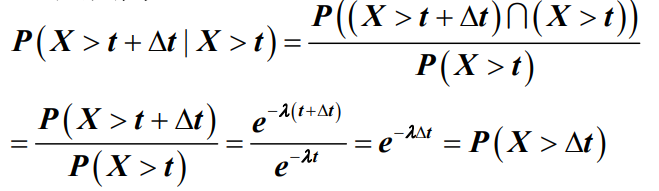
- 其中,t 和Δt是常数。对于排队论来说,这个性质可以看成是,剩余服务时间的分布独立于已经服务的时间,且与原分布相同
- 反过来,能满足公式的概率模型一定是负指数分布
- 高斯分布
- 设连续型随机变量X具有概率密度函数为:

- 其中,m和σ(>0)为常数。则称随机变量X服从高斯分布,或正态分布。其分布函数FX(x) 为:
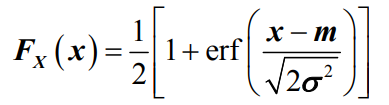
- 其中erf( )被称为误差函数
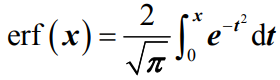
- 误差函数的泰勒级数展开式为:

- 随机变量X的均值为m
- 随机变量X的方差为σ
- 爱尔兰分布
- 设连续型随机变量X具有概率密度函数为:
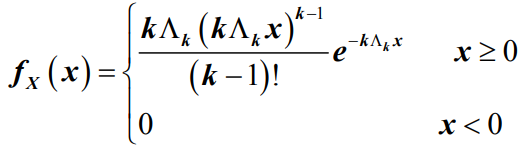
- 其中,Λk(>0)为常数,称为爱尔兰流强度,则称随机变量X服从参数为Λk的k阶爱尔兰分布。
- 其分布函数FX(x) 为:
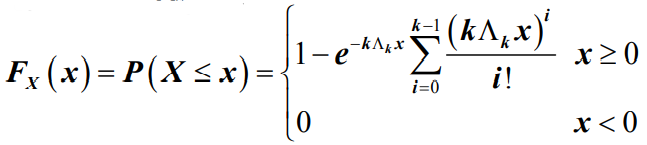
- 随机变量X的均值为:

- 随机变量X的方差为:
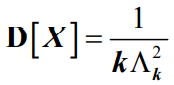
- 爱尔兰分布与负指数分布有着密切的关系。如果设随机变量X1, X2,…, Xk是k个相互独立的随机变量,且都服从相同参数为λ(>0)的负指数分布,那么随机变量X=X1+X2+…+Xk就是服从参数为Λk的k阶爱尔兰分布。对于公式中的参数Λk有:
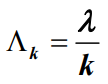
- 将Λk=λ/k代入到爱尔兰概率密度函数
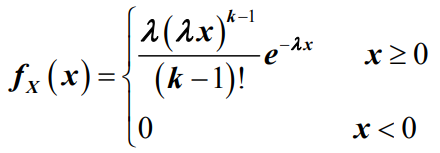
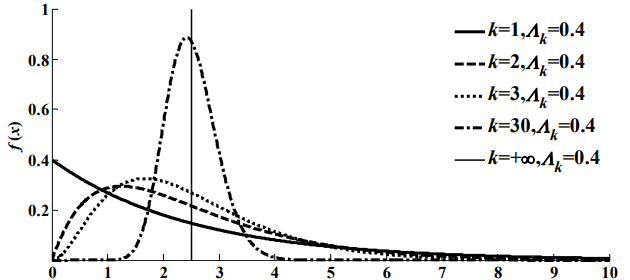
- 当k=1时,爱尔兰分布就化为负指数分布。当阶数k增大时,爱尔兰分布的图形逐渐变成对称的。当阶数k≥30时,爱尔兰分布就近似于高斯分布。而当k→∞时,
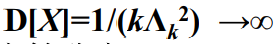 ,此时爱尔兰分布就转化为确定性分布
,此时爱尔兰分布就转化为确定性分布 - 这样,一个服从参数为λ的k阶爱尔兰分布的随机变量X,就可以根据k的取值在完全随机与完全确定的两种特性之间进行转换。这种特性对于研究通信网络是十分有意义的。下图为Λk=0.4时k取不同值时的爱尔兰分布概率密度曲线
- 爱尔兰分布提供了一种更为广泛的概率模型,它比负指数分布具有更大的适应性。
- 例如,k 个服务窗口串联(k 个服务阶段),每个服务时间服从相同参数的负指数分布,那么一个顾客接受 k 个服务窗口总共需要的服务时间就服从 k 阶爱尔兰分布。
- 由于它与负指数分布有着密切的联系,因此也就可以用负指数分布的特性去处理与爱尔兰分布有关的问题
- 广义爱尔兰分布
- 如果连续型随机变量X具有概率密度函数为:
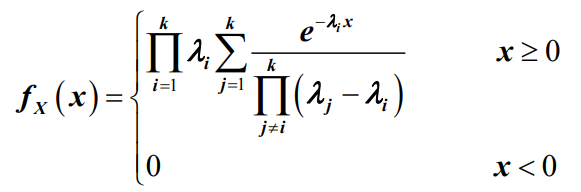
- 其中, λi (>0)为常数,则称随机变量X服从k阶广义爱尔兰分布
- 广义爱尔兰分布也与负指数分布有着密切关系
- 如果设随机变量X1,X2,…,Xk是k个相互独立的随机变量,并且各自服从参数为λi(>0)(i=1,2,…,k)的负指数分布,那么随机变量X=X1+X2+…+Xk就服从k阶广义爱尔兰分布
- 实际应用中经常使用二阶 (k=2)广义爱尔兰分布,此时的概率密度函数为:
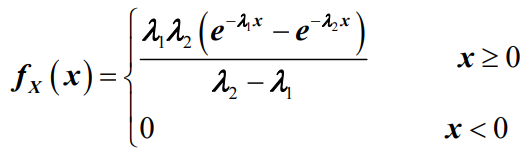
- 并定义此时的广义爱尔兰流强度为:

- 超指数分布
- 如果连续型随机变量X具有概率密度函数为:
- 超指数分布
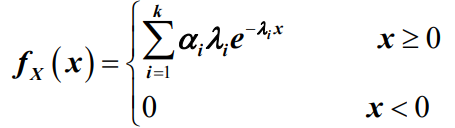
- 其中, λi(>0) 和 ai(>0)均为常数(i=1,2, …,k) ,且有正则条件
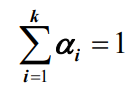
- 则称随机变量X服从超指数分布
- 超指数分布的分布函数为:
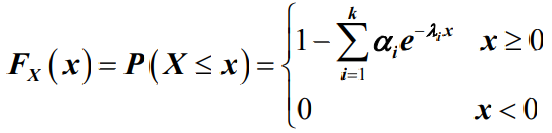
- 均值为
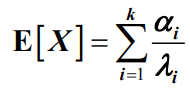
- 方差为
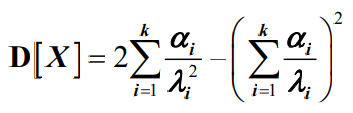
- 同样,超指数分布也与也与负指数分布有着密切的关系。
- 如果随机变量X1,X2,…,Xk是k个相互独立的随机变量,并且各自服从参数为λi(>0)(i=1,2, …,k)的负指数分布,随机变量X=Xi(i=1,2, …,k)的概率是ai,那么随机变量X就服从参数为λi和ai超指数分布。
- 或者说,单一事件重复发生,其间隔时间服从不同参数的负指数分布,且发生时间间隔为参数为λi的负指数分布的概率是ai,这种间隔时间分布就是超指数分布
5.2.5最简单流
- 前苏联数学家辛钦把处于统计平衡的电话呼叫流称为最简单流。
- 考虑单个输入过程,令N(t)表示在时间(0,t]内到达的顾客数,则{N(t),t≥0}是连续时间参数的随机过程。一般地,如果随机过程的统计特性与起始时刻无关,则称过程是平稳的。
下面的讨论均是平稳过程
如果{ N(t), t ≥ 0 }满足下列条件:
- 条件一:N(0)=0 ;
- 条件二:{N(t),t≥0}有独立增量,即对任取n个时刻有0<t1<t2< …<tn,随机变量N(t1) -N(0)、 N(t2) -N(t1) 、…、 N(tn) - N(tn-1)是相互独立的;
- 条件三:{N(t),t≥0}具有平稳增量,且对任意t≥0且Δt ≥0,有
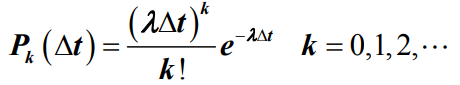
- 其中, λ(>0)为常数。如果满足上述条件,则称{N(t),t≥0}是最简单流,也称为泊松流、泊松输入或泊松过程
- 泊松流有如下四个特性:
- 性质一:平稳性
- 在[t, t+△t) 时间段内,到达k个顾客的概率只与△t有关,而与间隔的起始时刻t无关。用Pk(△t)表示在时间间隔△t内有k个顾客到达的概率,即有
- 性质一:平稳性
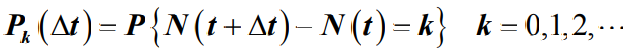
- 性质二:无后效性
- 顾客各自独立随机到达系统,在不相互重叠的时间段 [t, t+△t) 内,到达的顾客数量相互独立。也就是顾客到达具有马尔可夫特性。
- 性质三:普通性
- 在时间间隔△t内,有两个或两个以上顾客到达的概率是一个高阶无穷小量。
- 证明:


- 性质四:有限性
- 在任意有限区间内达到有限个顾客的概率为1。而且有
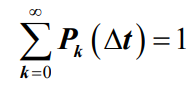
- 泊松流或近似于泊松流的事件在实际工程中经常会遇到,而且泊松流的数学处理是相对最简单的。- 因此泊松流常用于排队系统中的输入过程。大量研究结果表明,将电话呼叫当做泊松流来处理,所得到的分析结果是正确的!- 如果实际工程中的事件流与泊松流有较大出入时,可以用实际事件流的密度带入泊松流中,此时得到的结果也能满足一定的精度要求
- 例题
- 下面考察,当顾客按照泊松流到达时,其到达的时间间隔是服从什么样的分布?
- 设顾客到达时间间隔是一连续性随机变量T,其分布就是顾客到达时间间隔小于t的概率,也就是t内有顾客的概率分布
- 根据公式
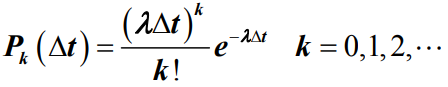 可知,在t内没有顾客的概率为:
可知,在t内没有顾客的概率为:
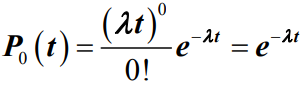
- 那么两相邻顾客到达的时间间隔分布函数为:

- 这样,其概率密度函数为
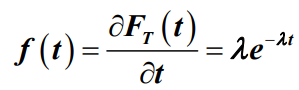
- 公式可以说明,随机变量T服从负指数分布,且顾客到达的平均时间间隔为:
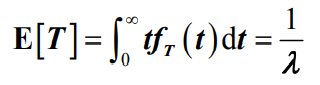
- 根据上面的推导可以得如下出结论
- 一个随机过程为泊松流,其到达时间间隔一定服从负指数分布。
- 反过来,一个随机过程的到达时间间隔服从负指数分布,那么这个随机过程一定是泊松流。
- “到达过程为泊松流”等价于“到达时间间隔服从负指数分布
- 于是有:一个输入过程是参数为的泊松流的充分必要条件为:顾客相继到达的时间间隔Ti(i=1,2,…)相互独立,且均为服从相同的负指数分布,即
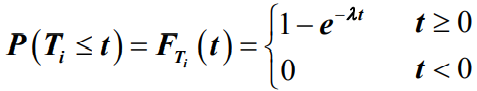
- 设有两个相互独立的泊松流,各自按照λ1、λ2的速率到达系统,那么其呼叫发生的概率分别为:
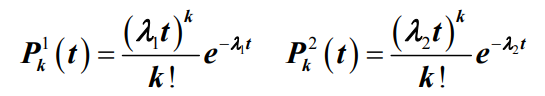
- 则合成呼叫发生数为k的概率为:
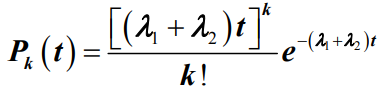
- 显然,两个分别按λ1、λ22的泊松流的合成等于呼叫发生率为λ1+λ2的泊松流
- 由此可以推广为一般的情况。若有k个各自任意速率为
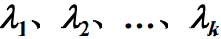 的独立泊松流,则复合流也是泊松流,其速率参数为:
的独立泊松流,则复合流也是泊松流,其速率参数为:
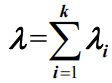
这个特性十分有用,在通信网中有许多信息源可以汇聚在一起,而每个信息源以各自的泊松速率产生呼叫或分组,这时就是一种泊松过程的合成现象
5.2.6生灭过程
生灭过程是用来描述输入过程为最简单流、服务时间为指数分布的一类最简单的排队模型。
- 假定某系统具有状态集E={0,1,2,…,K},令{N(t),t≥0}表示在时刻t时系统所处的状态,如果该随机过程在△t 时间后满足下列条件:
- 条件一:系统从k(0≤k<K-1)状态转移到k+1状态的概率为

- 条件二:系统从k(1≤k<K)状态转移到k-1状态的概率为

- 条件三:系统从k状态转移到
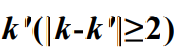 状态的概率为
状态的概率为
- 条件一:系统从k(0≤k<K-1)状态转移到k+1状态的概率为
- 则称随机过程{N(t), t≥0}是在E={0,1,2,…,K}上的有限状态生灭过程。其中,
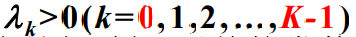 ,
,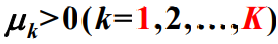 且均是与时间 t 无关的常数
且均是与时间 t 无关的常数 - 状态转移图

- 上图中的数字K代表系统状态,指的是系统中顾客数量
- 状态概率用
表示,即在 t 时刻系统中有 k 个顾客 的概率,也称瞬态概率
- 箭头代表状态间的转移关系,箭头旁的参数
和
代表状态转移率
- 对于排队系统,系统状态生长意味着顾客的到达,而系统状态灭亡就意味着顾客离开。显然有
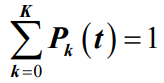
- 当系统状态为可列无限状态E={0,1,2,…}时,则随机过程{N(t), t≥0}被称为无限状态生灭过程,其状态转移图如下所示

- 此时也有:

- 系统状态概率与状态转移率的关系是怎样的呢?
根据生灭过程的定义,设系统在t时刻处于k状态,那么在t +△t时刻时,系统可能处于状态是以下四种状态之一
- k状态
- k-1状态
- k+1状态
- 其它状态
情况一:当系统从 t 时刻到 t + Δt 时刻由k状态转移到k状态,发生此种情况的概率为
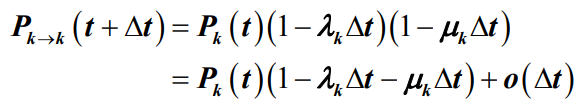
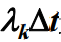 是在 Δt 时间内 k 状态转移到 k+1 状态的概率,
是在 Δt 时间内 k 状态转移到 k+1 状态的概率,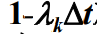 就是在 Δt 时间内 k 状态不转移到 k+1 状态的概 率(不生)
就是在 Δt 时间内 k 状态不转移到 k+1 状态的概 率(不生)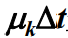 是在 Δt 时间内 k 状态转移到 k-1 状态的概率,
是在 Δt 时间内 k 状态转移到 k-1 状态的概率,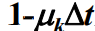 就是在 Δt 时间内 k 状态不转移到 k-1 状态的概 率(不灭)
就是在 Δt 时间内 k 状态不转移到 k-1 状态的概 率(不灭) - o(Δt) 表示Δt高阶项;Pk(t)是系统在 t 时刻的瞬态概率
- 情况二:当系统从 t 时刻到 t+Δt 时刻由k-1状态转移到k状态,发生此种情况的概率
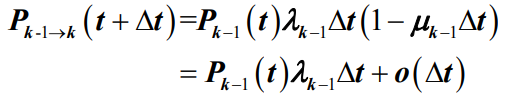
 是在 Δt 时间内 k-1 状态转移到 k 状态的概率(有生);
是在 Δt 时间内 k-1 状态转移到 k 状态的概率(有生);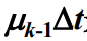 是在 Δt 时间内 k-1 状态转移到 k-2 状态的概率,
是在 Δt 时间内 k-1 状态转移到 k-2 状态的概率,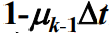 就是在 Δt 时间内 k-1 状态不转移到 k-2状态的概率(不灭);
就是在 Δt 时间内 k-1 状态不转移到 k-2状态的概率(不灭);- o(Δt)表示Δt的高阶项;
 是系统在 t 时刻的瞬态概率
是系统在 t 时刻的瞬态概率- 情况三:当系统从t时刻到t+Δt时刻由 k+1 状态转移到 k 状态,发生此种情况的概率为
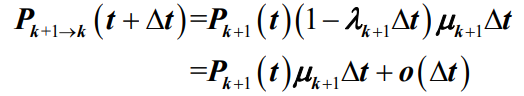
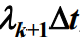 是在 Δt 时间内 k+1 状态转移到 k+2 状态的概率,
是在 Δt 时间内 k+1 状态转移到 k+2 状态的概率, 就是在 Δt 时间内k+1状态不转移到k+2状态的概率(不生);
就是在 Δt 时间内k+1状态不转移到k+2状态的概率(不生);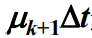 是在t时间内 k+1 状态转移到 k 状态的概率(有灭);
是在t时间内 k+1 状态转移到 k 状态的概率(有灭);- o(Δt)表示 Δt 的高阶项;
 是系统在t时刻的瞬态概率
是系统在t时刻的瞬态概率- 情况四:当系统从t时刻到 t+Δt 时刻在从除k-1状态、k状态和k+1状态之外的其它状态转移到k状态,发生此种情况概率可以根据公式
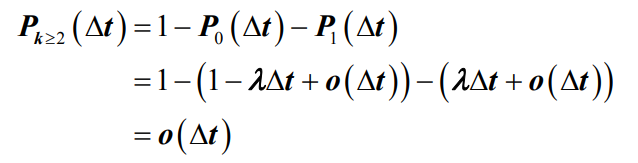 得出:
得出:
- 情况四:当系统从t时刻到 t+Δt 时刻在从除k-1状态、k状态和k+1状态之外的其它状态转移到k状态,发生此种情况概率可以根据公式
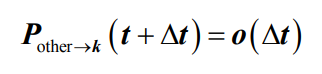
- 即最简单流的性质三(普通性)

- 由全概率公式,对于k≠0时,在t+Δt时刻处在k状态的状态概率为:
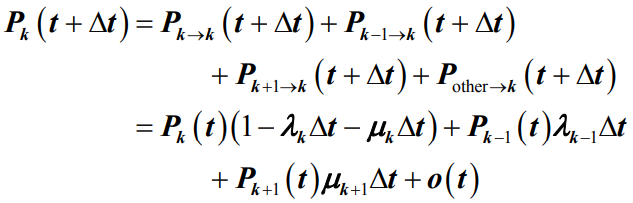
- 同理,当k=0时,在t+Δt时刻处在k状态的瞬态概率为

- 于是有
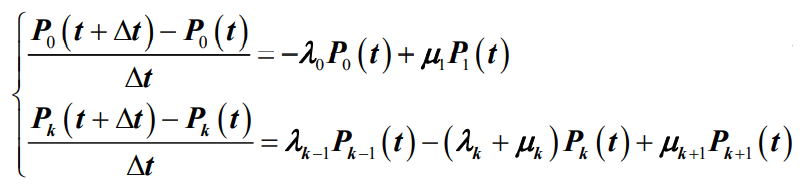
- 公式忽略了o(Δt)项。令t →0并取极限,就得到了生灭过程的微分差分方程组
- 对于在E={0,1,2,…,K}上的有限状态生灭过程有:
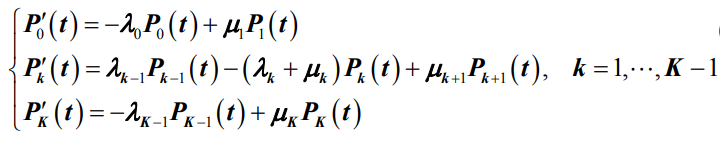
- 对于在E={0,1,2,…}上的无限状态生灭过程有:

两个公式中是关于瞬态概率Pk(t)的微分差分方程,由于求解该微分差分方程比较困难,即便求得一般也很难使用。因此,排队论中主要研究系统处于稳定状态下的工作情况
稳定状态是一种统计状态,它是指系统运行充分长时间后,系统初始状态的影响基本消失,此时系统状态不再随时间变化。
- 系统一旦进入了稳定状态,生灭过程就具有了马尔可夫性质。
- 稳态概率就是系统进入稳定状态时的概率,与起始时间t无关。分析稳态概率是排队系统的基础。
- 稳态概率Pk定义为:
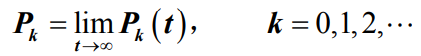
为了求解系统稳态概率Pk ,需要用到下面的定理
定理一(生灭过程微分差分方程组微分极限存在性)
- 在公式
 存在的条件下有
存在的条件下有
- 在公式

- 证明:由上面定理知,微分差分方程组等式右边的极限存在,于是对于k=0,1,2,…当t→+∞ 时
 的极限存在。若存在一个状态k使得
的极限存在。若存在一个状态k使得
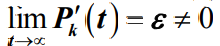
- 不妨设ε>0,则对所取的ξ (0<ξ<ε),存在t0>0,当t≥t0时有 ,当
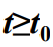 时有
时有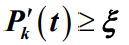 ,于是有
,于是有
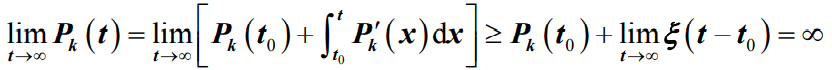
- 这与
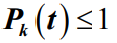 相矛盾,故定理一得证
相矛盾,故定理一得证- 定理二(生灭过程微分差分方程组解的存在性)
- 对于在E={0,1,2,…,K}上的有限状态生灭过程,若满足条件:
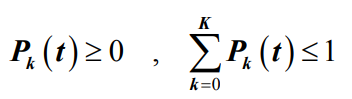
- 则对任意给定的初始条件,公式的解存在、惟一。而且有
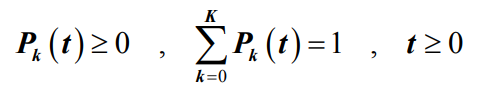
- 对于在E={0,1,2,…}上的无限状态生灭过程,若满足条件

- 则对任意给定的初始条件,公式的解存在、惟一。而且有
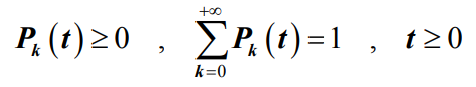
- 定理三(极限定理)
- 对于在E={0,1,…,K}上的有限状态生灭过程,{Pk , k=0 ,1,…,K}存在,与初始条件无关,而且有:
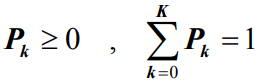
- 即{Pk , k= 0,1,…,K}为平稳分布
- 对于在E={0,1,…}上的无限状态生灭过程,若有下式成立:

- 则{Pk , k= 0,1,…,K}存在,与初始条件无关,而且有

- 即{Pk , k= 0,1,…,K}为平稳分布
- 这样,根据上面三个定理,令t→+∞并取极限就可以得到
- 在E={0,1,…,K}上的有限状态生灭过程,公式
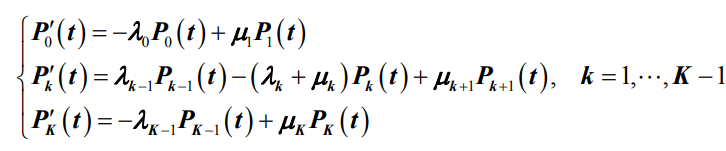 转化为线性差分方程组:
转化为线性差分方程组:
- 在E={0,1,…,K}上的有限状态生灭过程,公式
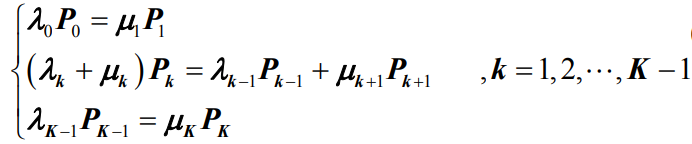
- 根据公式
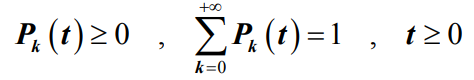 可得
可得
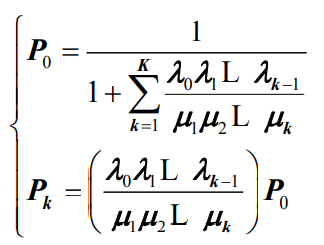
- 特别地,当
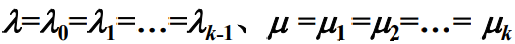 时,只要
时,只要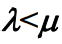 ,则公式可以简化为
,则公式可以简化为

- 在E={0,1,…}上的无限状态生灭过程,公式
 转化为线性差分方程组
转化为线性差分方程组

- 根据公式
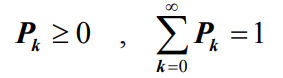 可得
可得
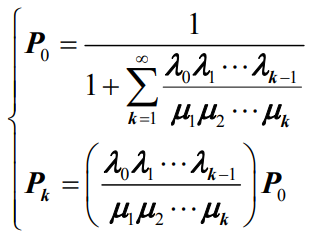
- 特别地,当
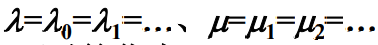 时,只要
时,只要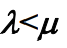 ,则公式可以简化为
,则公式可以简化为
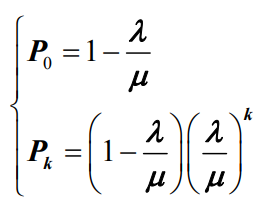
- 这里需要说明的是,在排队论中,常将公式
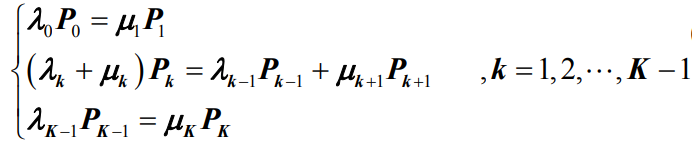 和公式
和公式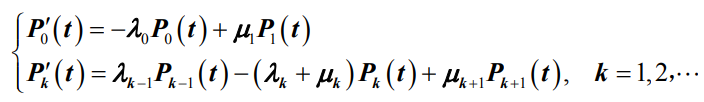 称为平衡方程
称为平衡方程 - 所谓平衡可以理解为,当系统运行到稳定状态时,对于任意状态来说,进入该状态的概率等于离开该状态的概率。
- 换句话说,如果系统是稳定的,那么系统中任意的一个状态也是平衡的,也就是‘流入=流出’。这就是系统在稳定状态下统计平衡原理。
- 平衡方程是研究排队论的基础,利用平衡方程求解出的初始概率
和稳态概率
是十分重要的,在后面的内容中将会经常用到