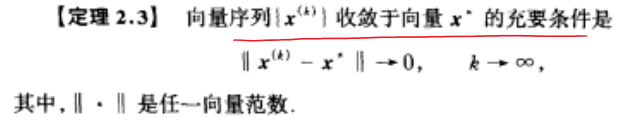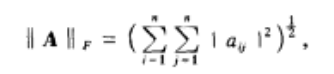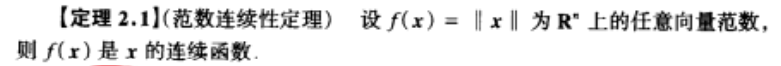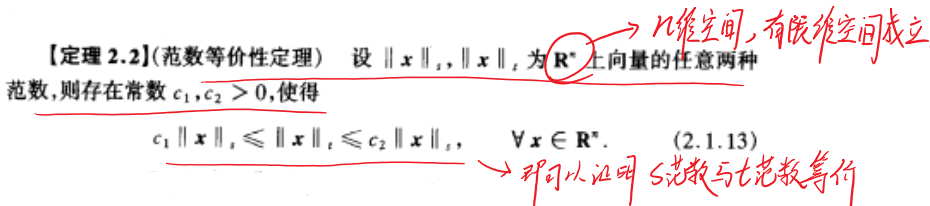• 为了研究解的误差分析和迭代法的收敛性,我们需要对n维向量和n阶方阵引进某种度量
    • 向量范数和矩阵范数
  • 范数类似于向量的模，模是向量的一种范数
  • 用于衡量该向量/矩阵的大小（高维空间的距离定义）

  • 空间➡定义范数➡比较大小

    向量范数

    image.png

    矩阵范数

  • 矩阵范数为向量范数的类比

image.png

  • 矩阵的常用范数较少
  • 例如F范数

image.png

相容性定理

  • 常常不单独考虑矩阵的范数，而更常与向量放一起考虑

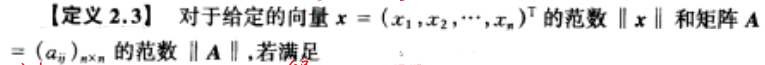
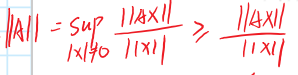
image.png
image.png

  • 则称此矩阵范数与向量范数是相容的

    从属范数

  • 由相容性定理

image.png

  • sup为上确界，即上界中最小的那一个

image.png

  • 进一步可知

【数值分析】向量范数与矩阵范数 - 图8

  • 此时求出的||A||即为矩阵的范数，也称为由向量范数产生的从属范数或算子范数
  • 从属范数一定与所给定的向量范数相容

  • 但是相容的向量范数不一定从属

  • 常见的从属范数有

image.png
image.png
image.png

连续性定理

image.png

等价性定理

image.png

收敛性定理

image.png