特征值

• 为A的特征值，x为A对应于的特征向量
• A的特征值是方程

• 的根，此方程为A的特征方程
• n次多项式，n阶方阵有n个多项式
• 但是行列式转换成多项式方程繁琐
• 存在定理

• 推论

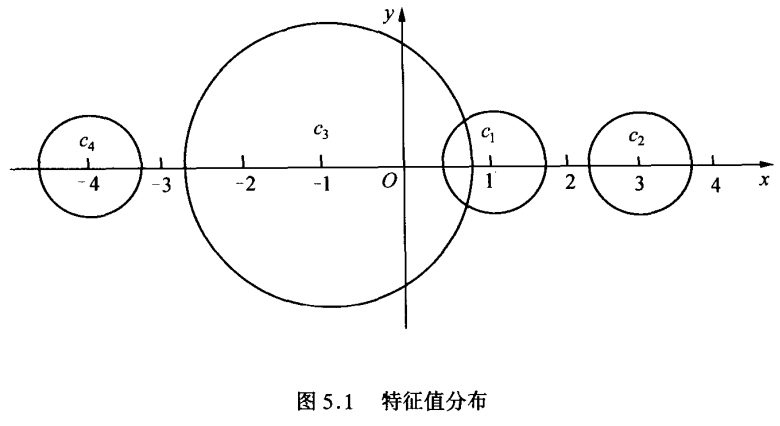
格尔什戈林圆盘

• 格尔什戈林圆盘（Gerschgorin）定理

• 即对角线上的值为圆心
• 每一行上除了对角线上的值以外的元素求和为半径
• 例题

乘幂法

• 设矩阵A具有n个线性无关的特征向量,且对应的特征值可以依序排列如下:

• 求按模最大的特征值和对应的特征向量
• 设A对应于的特征向量为,由于它们线性无关,故可以构成n维线性空间的一组基底。因此，任一向量可以被这n个向量线性表出

• 要求解的是按模最大的特征值和它对应的特征向量
• 如果是的良好近似，则相应于的系数的绝对值应该远远大于其他系数
• 用作用于，则可经迭代得到一个向量序列

• 中所含的按模最大的特征值的那一项，将随m的增大而在右式中占优势，即为乘幂法依据的原理
• 由于是严格占优的，所以当时

• 即得到定理

• 因此当m充分大时，将有

• 即迭代向量为的特征向量的近似向量(除一个因子外)
• 对任意一个不与正交的向量

• 当选择y是第i个分量为1，其余分量均为零的向量时，即，则式变为

• 由此求得A的按模最大的特征值的近似值
• 当m充分大时，用乘幂法进行计算，将变得很大(或变得很小)，很容易发生机器上溢出(或机器下溢出)
• 为此，可以将迭代产生的向量序列加以规范化来避免溢出
• 具体做法是，对选取的初始向量，令

• 其中，符号max(v)表示向量v的绝对值最大的分量
• 因此则有

• 当时

• 因此规范化的向量序列收敛到经过规范化以后的向量

• 即规范化以后的向量序列，其绝对值最大的分量以为极限