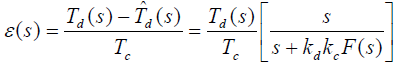- 扩频接收机的环路：
- （1）载波环路： 捕获和跟踪 → 采用锁相环技术
- （2）码环路： 同步捕获和跟踪 → 采用延时锁定环路
- 均是反馈环路来实现跟踪作用
延时锁定环（Delay Locked Loop，DLL）
扩频系统码跟踪回路分类
- 相干同步跟踪回路：
- 利用接收信号相位信息（载波频率和相位精确已知）
- 非相干同步跟踪回路：
- 不利用接收信号相位信息（载波频率未知）
- 相干同步跟踪回路：
延迟锁定鉴别器都要利用接收信号与本地参考信号两个不同相位（超前和滞后）之间相关值的差值
根据相关运算的实现方式，跟踪回路可分为：
- 全时间相关同步跟踪回路：
- 用两个独立相关器构成延迟锁定鉴别器
- τ-抖动相关同步跟踪回路：
- 单个相关器分时工作构成延迟锁定鉴别器
- 全时间相关同步跟踪回路：
环路研究涉及的几方面问题：
- 稳态跟踪特性- Tracking Performance
- 线性模型；跟踪误差方差；比较各种环路精度；
- 暂态捕获性能- Acquisition (Transient) Behavior
- 相平面；暂态牵引响应；
- 失锁性能- Mean Time to Lose-of- Lock
- 环路保持锁定的时间；
- 稳态跟踪特性- Tracking Performance
DLL设计要求：
数学模型
- 设基带系统为：
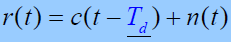
- 式中：
是环路跟踪的未知时延量， 
的最大似然估值是似然方程之解
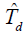
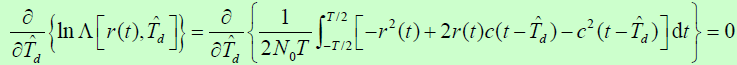
- 式中：
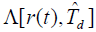是似然函数；
是 n(t) 的功率谱密度。 - 由于
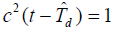，故有
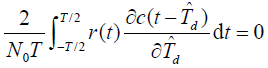
- 与此等效，最大似然方程的解值
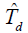应满足：
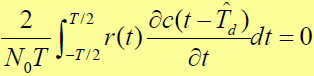
结论：
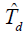的最佳估值是由接收信号 r(t) 与本地码 c(t) 的时间导数求相关而得。- 对扩频码同步跟踪必须要采用闭合环路，即接收信号 r(t) 与本地码 c(t) 导数之间相关值经闭合环路后应为0
- 可以用 c(t) 的滞后量与超前量之间的差值来近似导数，采用闭合环路，通过调整值达到对时延的跟踪。
研究四种环路：
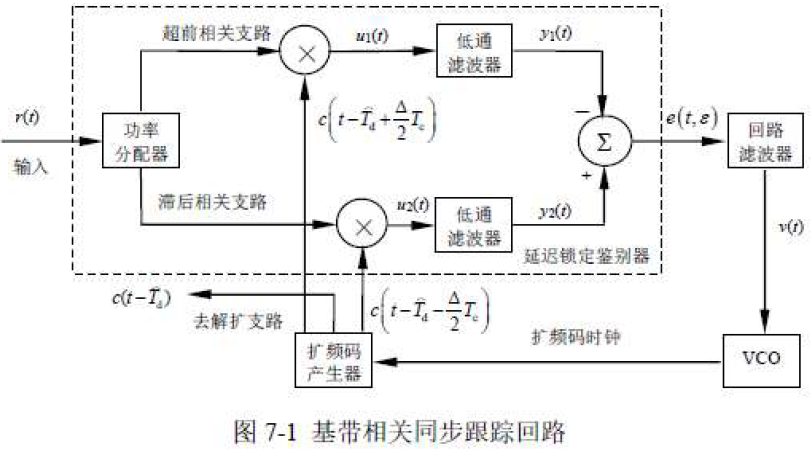
也称基带相关延迟锁定回路。
- 由延迟锁定鉴别器、回路滤波器、压控振荡器(Voltage Control Oscillator，VCO)与扩频码产生器等组成。
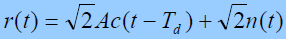
- n(t) 是均值为零、双边功率谱密度为
的基带高斯白噪声 - 无噪声情况下，超前与滞后相关支路乘法器输出为：
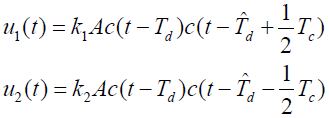
- 式中: k1 与 k2 为超前与滞后相关支路乘法器增益。假设支路完全平衡、参数完全相等，即 k1=k2=k
- 码自噪声忽略不计
与
中的时变分量称为码自噪声。由于扩频系统通常要在强干扰或噪声环境下工作，而码自噪声中的大部分分量被相关支路中的低通滤波器滤除，输出的码自噪声功率远低于干扰或热噪声功率，故在同步跟踪回路分析中忽略码自噪声影响。
回路误差跟踪信号：
与
的直流(缓变)分量通过相关支路中的低通滤波器形成回路的跟踪误差信号。其直流分量为：
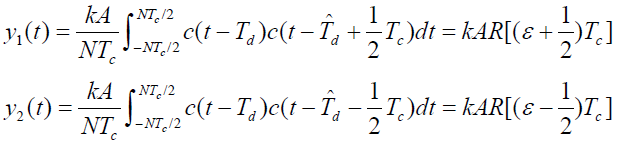
- 式中：
是 c(t) 的周期，而
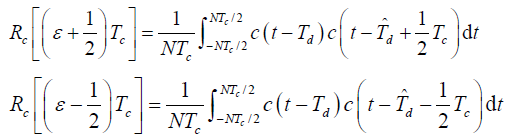
式中：
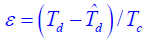是相对时延误差或相对跟踪误差延迟锁定鉴别器的输出是两相关支路低通滤波器输出
与
之差
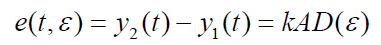
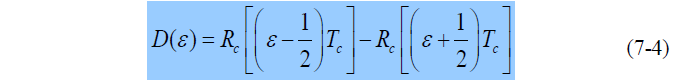
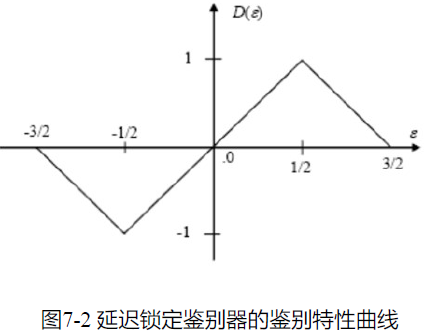
- D(ε) 直接反映出同步跟踪回路输出信号的时延估值
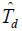对输入信号的时延
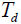的跟踪误差，称为基带相关同步跟踪回路延迟锁定鉴别器的鉴别特性曲线，简称S曲线。 - 扩频码 c(t) 周期很长时，自相关函数近似为：
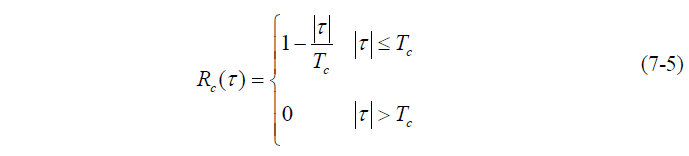
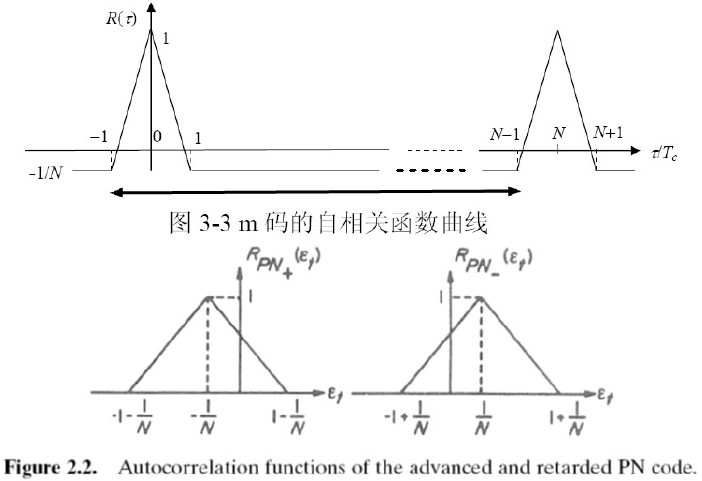
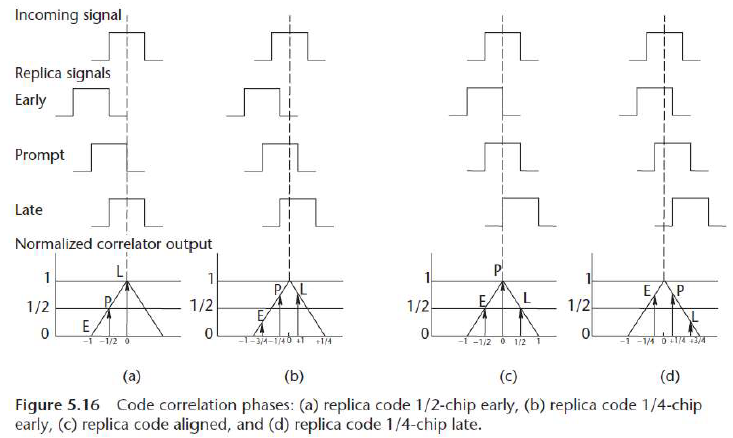
- 将(7-5)带入式(7-4)得：
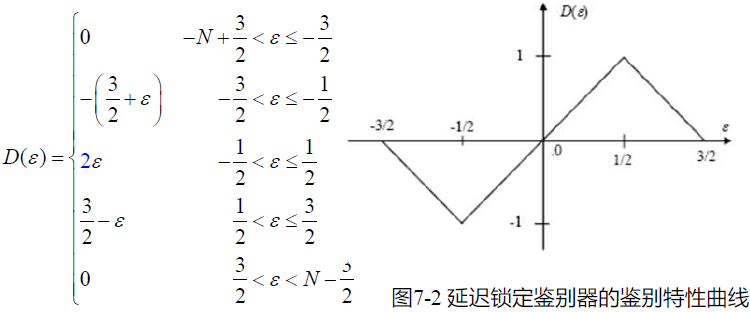
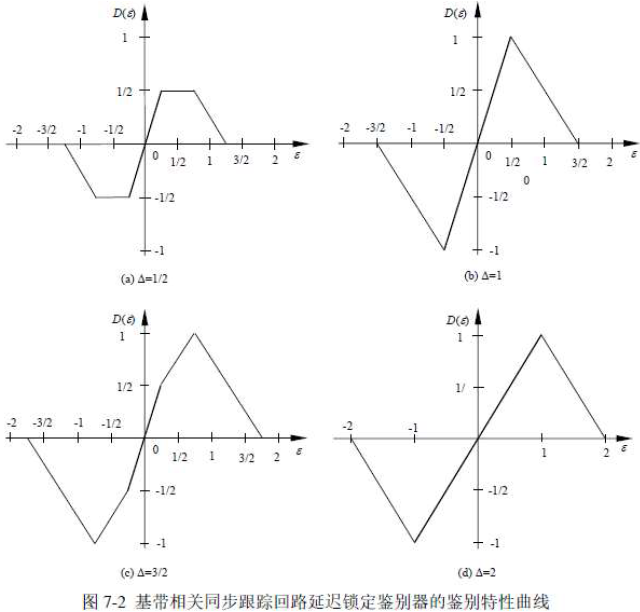
- S 曲线的另一解释：
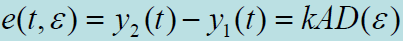
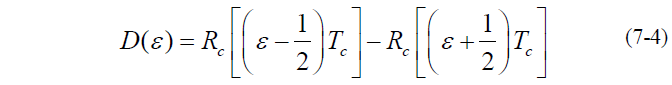
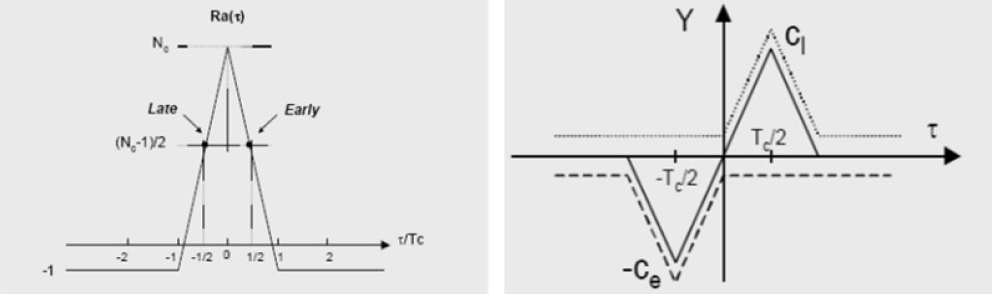
- 通常把 D(ε) 与 ε 呈线性关系的区域作为跟踪回路的正常工作区域
- 在超前与滞后相关支路的本地参考码差一个码元时，基带相关同步跟踪回路的正常工作区域为
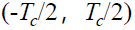
- 超前与滞后相关支路的本地参考码差可以小于一个码元
7.2.2 基带相关同步跟踪回路的数学模型
- 设回路滤波器线性时不变，传递函数为 F(f)，回路控制信号为 LF 输出：
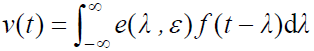
- 回路误差信号经过回路滤波器形成控制信号，通过控制 VCO 输出信号频率来调整本地参考码相位，达到跟踪接收扩频码。同步跟踪回路反映的是调节量
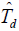与输入信号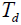
之间的关系。 可采用与锁相环路相类似分析方法。
压控振荡器方程表示VCO输出信号频率与控制信号关系：
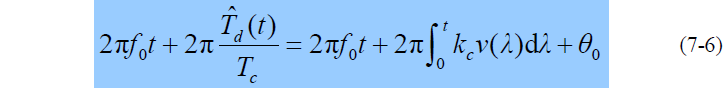
- 式中：
- 令
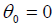，采用Heaviside（亥维赛）算子
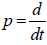，则有：
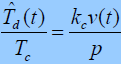
- 若回路内噪声为
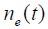，则延迟锁定鉴别器输出为：
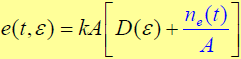
- 又有
- 同步跟踪回路的非线性微分方程为：
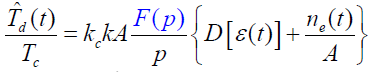
- 回路跟踪误差
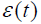为：
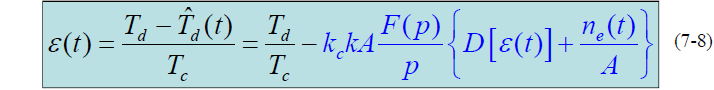
- 非线性等效电路模型：
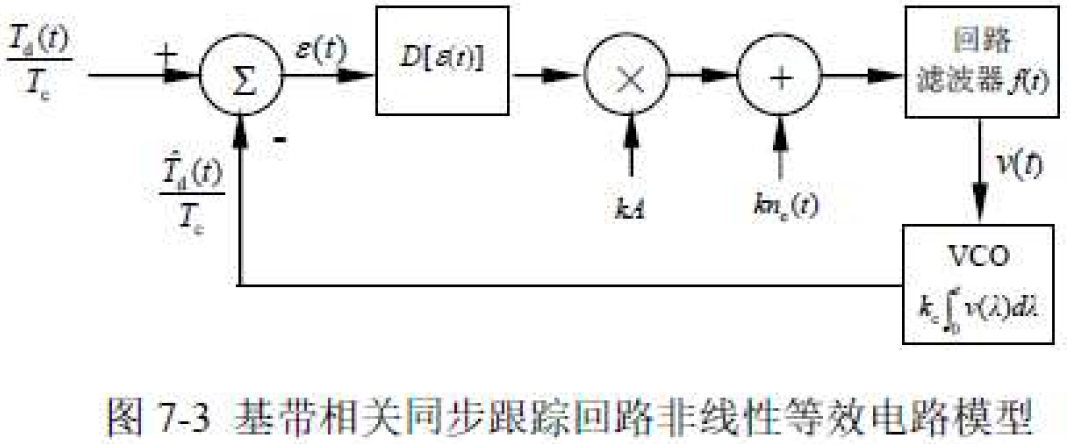
求解回路闭环传输函数：
- 手段：非线性方程线性化处理
- 回路锁定时，跟踪误差 ε(t) 较小，延迟锁定鉴别器工作在线性段，输出是跟踪误差的线性函数，即
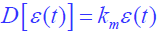，故系统模型简化为：
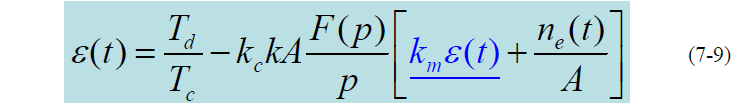
- 式中，
为鉴别特性曲线在原点附近的斜率，
- 线性等效电路模型（小跟踪误差时）：
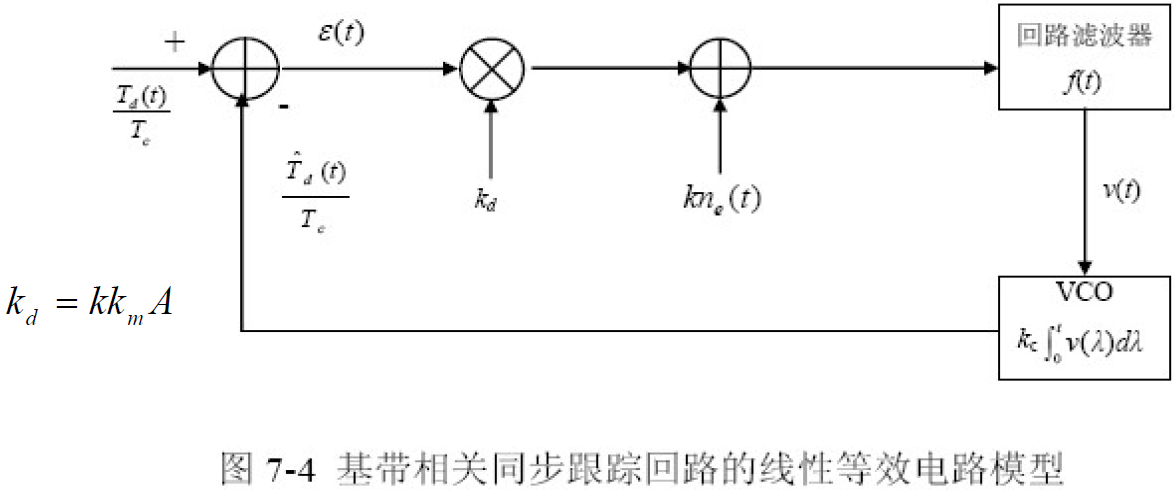
- 令
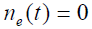，得：
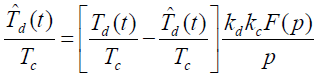
- 拉普拉斯变换得：
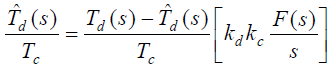
- 同步跟踪回路闭环传输函数：
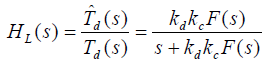
- 同步跟踪误差拉氏方程：
7.2.3 基带相关同步跟踪回路的噪声性能
- 目标：
- 跟踪回路的跟踪抖动由回路内噪声引起。
- 噪声情况下，跟踪回路的跟踪均方误差（跟踪抖动）与回路信噪比的关系如何？
- 假设：
- 仅考虑进入回路的高斯白噪声。忽略影响较小的码自噪声。
- 推导：
- 环路内存在噪声时，超前/滞后支路输出为：
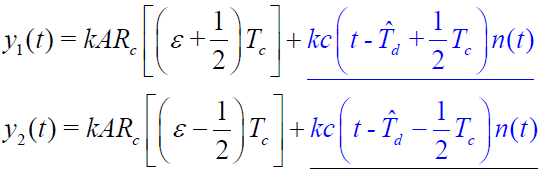
- 延迟锁定鉴别器输出：
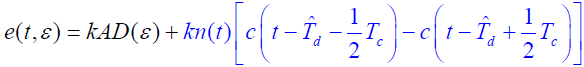
- 回路内噪声：
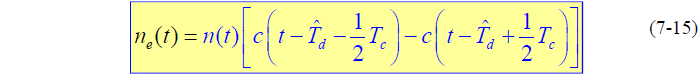
计算
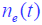的功率谱密度：- 方法：
- 自相关函数与功率谱密度函数互为傅氏变换对。
- 自相关函数为：
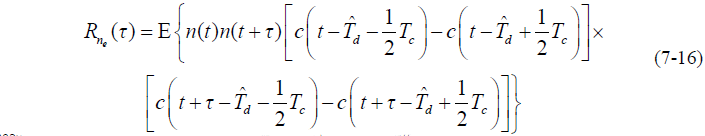
- 若噪声 n(t) 和扩频码 c(t) 相互独立，则有：
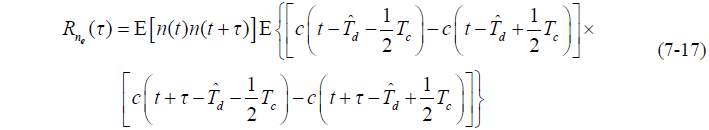
- 由于 n(t) 是功率谱密度为  的高斯白噪声，则有
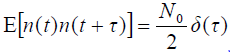
- 故有：
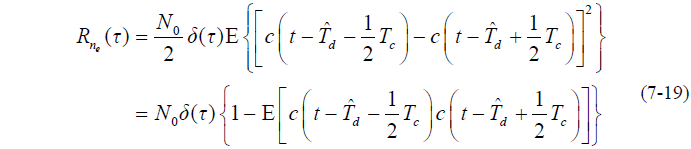
- 由于：
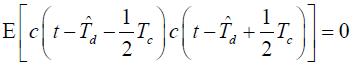
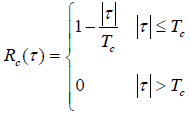
- 故有：
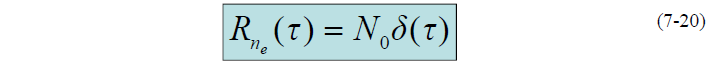
- 的双边功率谱密度函数为：
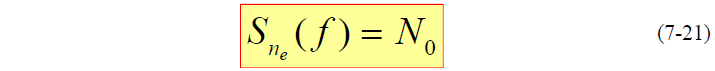
- 由(7-21)和式(7-15)知， 仍是白噪声，但不再是高斯白噪声。
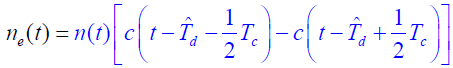
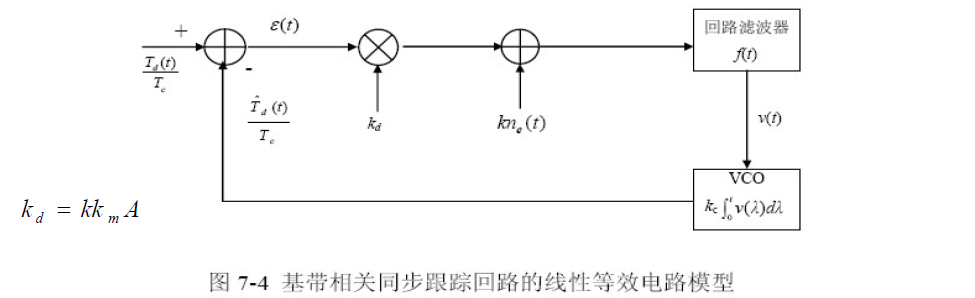
- 在同步跟踪回路处于锁定状态时，跟踪误差较小，回路可以采用线性等效电路模型。- 在线性电路模型的情况下，可以将噪声折算到闭合回路的输入端(利用叠加定理)，通过回路的闭环传输函数求出噪声通过回路后的响应。- 将回路噪声折算到闭合回路输入端时，有：
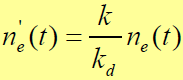
- 折算后的回路等效电路模型为：
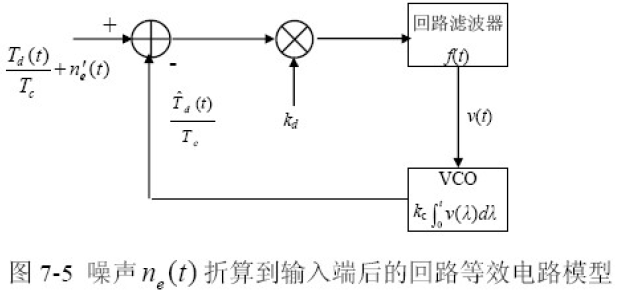
- 跟踪抖动的功率谱密度函数就是噪声 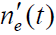 的功率谱密度函数与延迟锁定回路闭环功率传输函数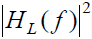的乘积，即等效噪声经过系统后的功率谱密度为：
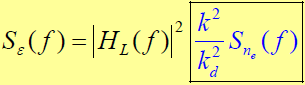
- 跟踪误差 ε(t )的方差为：
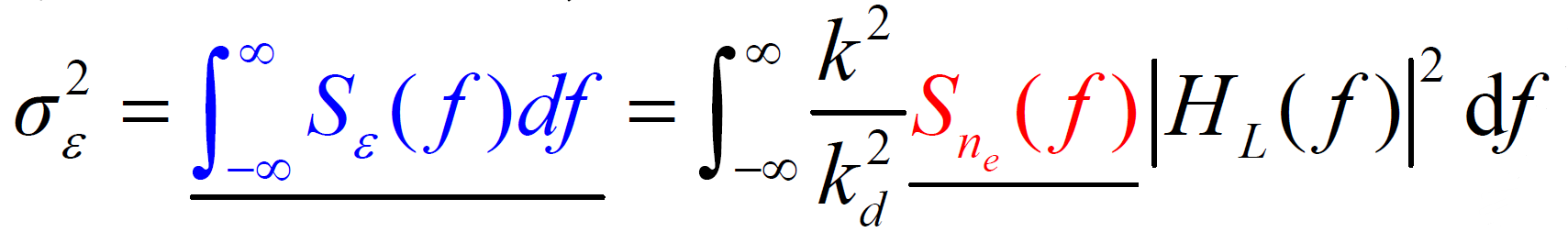
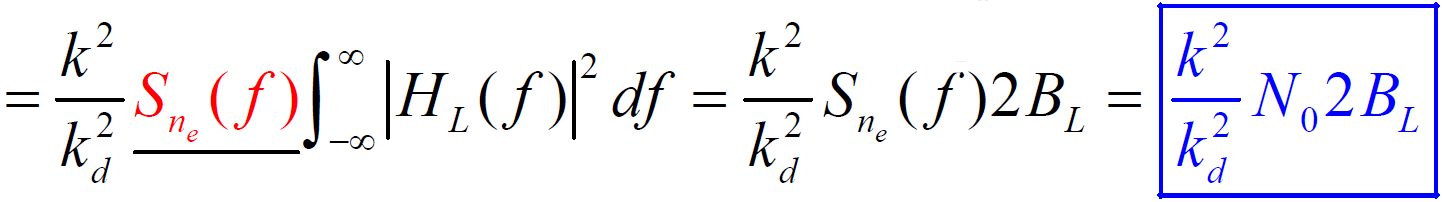
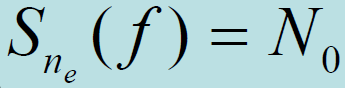
- 其中：
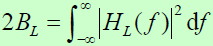
- 称为同步跟踪回路的双边等效噪声带宽，Hz- 因此，回路跟踪抖动为：
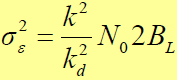
- 同步跟踪回路内信号功率为：
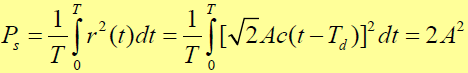
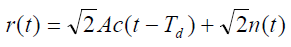
- 故回路信噪比为：
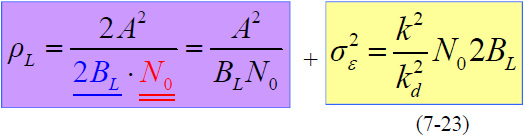
- 由于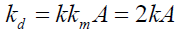 ，有：
- 结论：
成正比，而
与回路滤波器的传输函数有关。回路滤波器带宽越宽，等效噪声带宽就越宽，跟踪抖动就越大。减小跟踪抖动，要求回路滤波器带宽越窄越好。
，同步跟踪回路可能会失锁，导致环路不能有效地跟踪。
- 基带相关同步跟踪回路存在的问题：
- 扩频系统通常都是在信噪比非常低的环境中工作，解扩前完成解调很困难。另外调制是相干的，解调之前必须提取相干载波，在信噪比非常低的条件下，提取相干载波非常困难。
- 基带相关同步跟踪回路分析时，忽略了信息d(t)的存在。当信息存在时，延迟锁定鉴别器输出的信号不仅与回路跟踪误差有关，同时也是信息的函数。
- 使用基带相关同步跟踪回路不能适应这种工作场景。
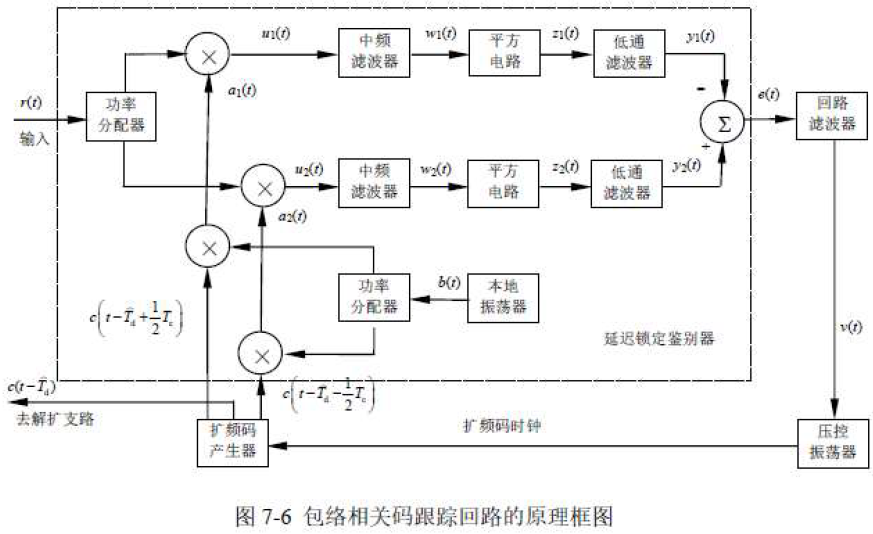
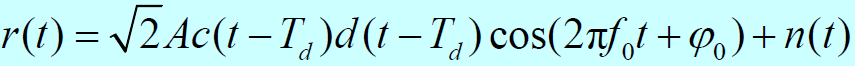
- 本地振荡器输出：
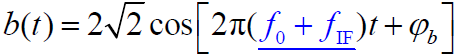
- 本地输入相关器信号：
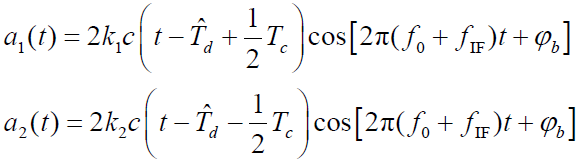
- 【假设】两支路中各部件的增益为1。延迟锁定鉴别器的两支路完全平衡、参数完全相等，即
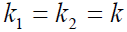
- 【忽略噪声情况】，延迟锁定鉴别器的乘法器输出：
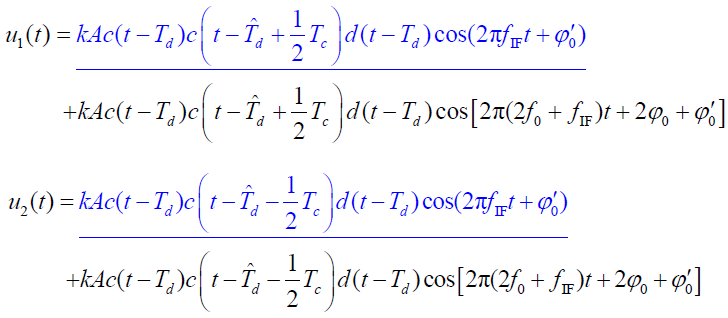
- 【假设】
- ① 中频滤波器中心频率为
，单边等效噪声带宽是
- ② 扩频码 c(t) 、信息信号 d(t) 和载波相位
均相互独立 ③ 设中频滤波器带宽正好让
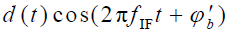通过在信号
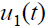中，只有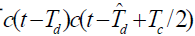
的直流分量与的乘积能通过中频滤波器
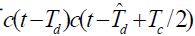的其他分量与
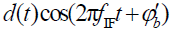的频谱进行卷积后，落在中频滤波器的通带外。
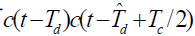的直流分量：- 直流分量是在一个周期内对时间求平均，即：
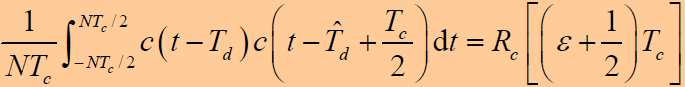
- 同理：
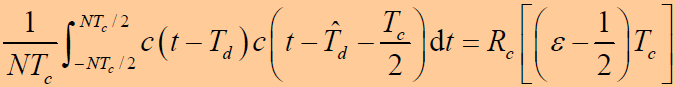
- 两支路中频滤波器输出：
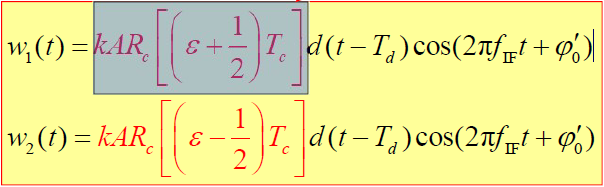
- 框中部分为直流分量
- 平方器件输出:
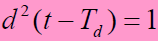
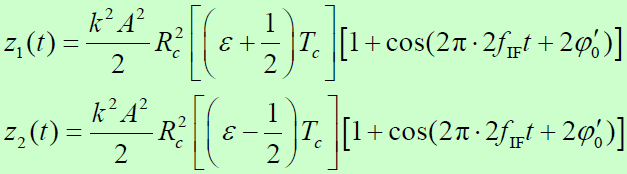
- 低通滤波器输出：
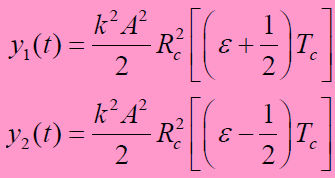
- 延迟锁定鉴别器输出：(鉴别特性曲线）
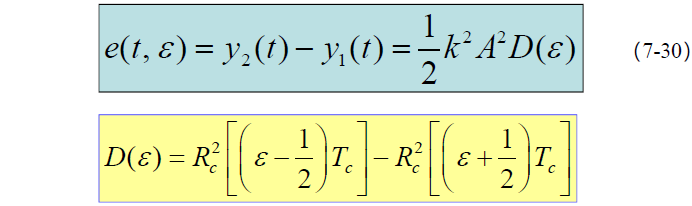
- 若系统
较高，则有：
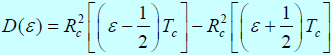
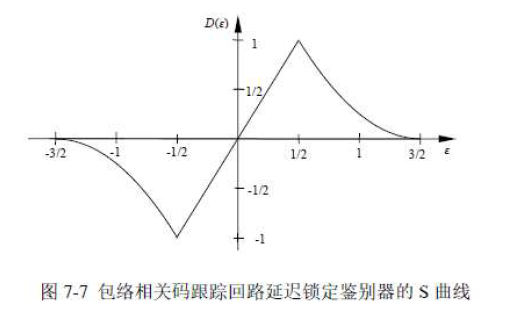
- 得到：
- 包络相关同步跟踪回路延迟锁定鉴别器S曲线：
7.3.2 包络相关同步跟踪回路的数学模型及跟踪抖动
- 【忽略噪声】，延迟锁定鉴别器输出：(鉴别特性曲线）
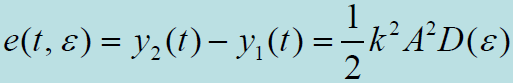
- 【目标】
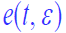中的噪声分量对环路的影响？
- 【忽略码自噪声，仅考虑高斯白噪声影响】
- 设输入噪声是带限零均值高斯白噪声，双边功率谱密度是
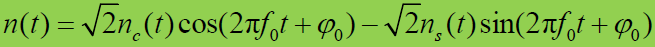
- 超前与滞后相关支路乘法器输出噪声分量为（忽略
项）
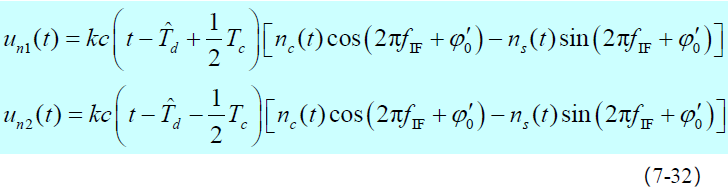
- 令
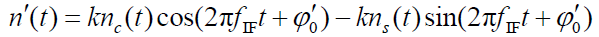
- 则有：
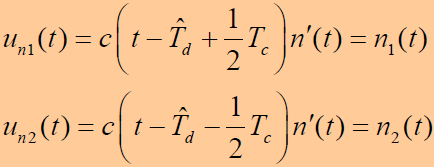
- 由于噪声
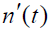和扩频码 c(t) 相互独立，故进入中频滤波器的噪声功率谱为它们功率谱的卷积：
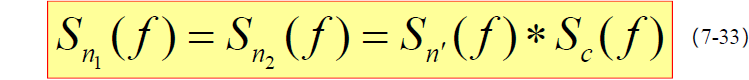
- 由于中频滤波器等效噪声带宽都远小于输入噪声带宽与扩频码带宽，在中频滤波器等效噪声带宽内，扩频码功率谱密度函数近似认为是常数。
- 中频滤波器输出噪声可认为是窄带高斯噪声，形式上可表示为：
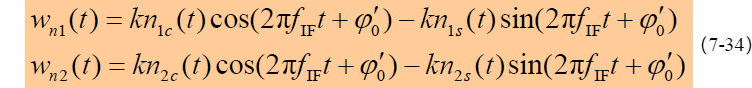
- 则，功率谱为：
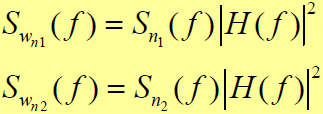
- 式中，H(f)是中频滤波器的传输函数
- 由于中频滤波器等效噪声带宽远小于扩频码带宽，有：
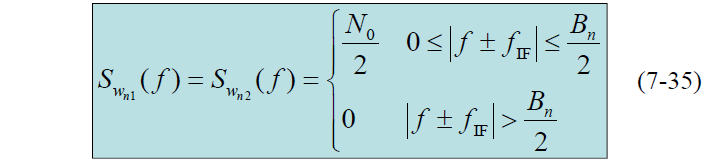
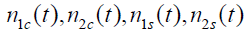功率谱形状相同，仅仅是中心频率位于零频率处
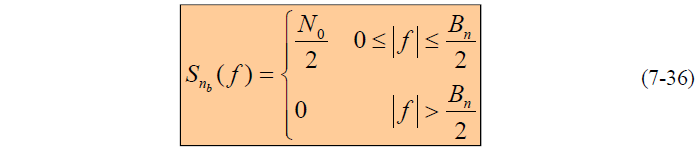
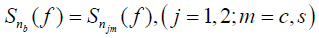为
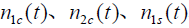和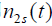
的功率谱密度- 中频滤波器的输出：（信号＋噪声）
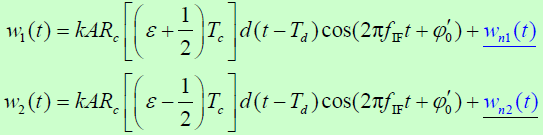
- 平方、低通滤波后为：
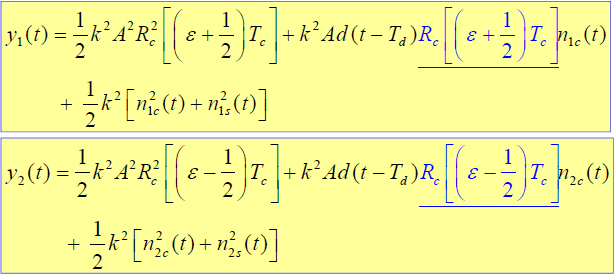
- 回路延迟锁定鉴别器输出：
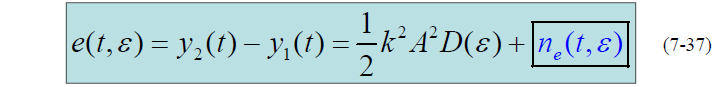
- 其中：
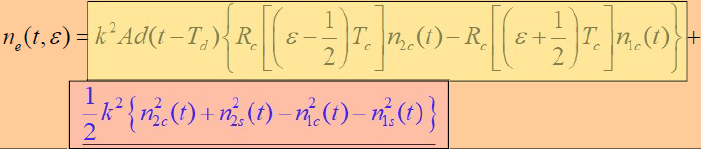
- 第一项：信号与噪声通过回路延迟锁定鉴别器发生相互作用后的输出。
- 第二项：噪声分量通过回路延迟锁定鉴别器后的输出。
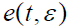的功率谱密度：
- 其中：
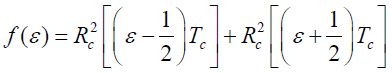
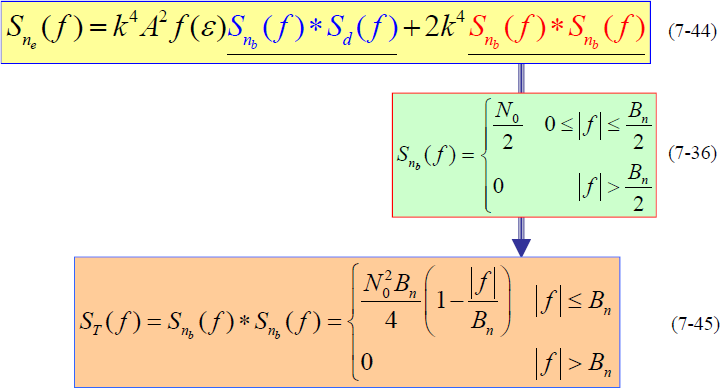
- （7-43中）：
- 第一项：环路跟踪误差信号分量
- 第二项：噪声分量
- 令
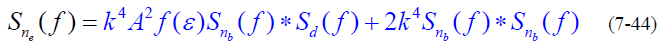
- 讨论其中的噪声分量：
- 在接收信号中没有数据调制情况时，即 d(t)=1
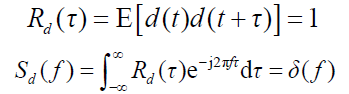
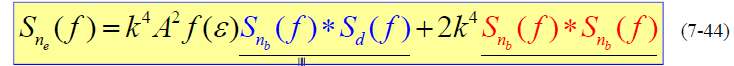
- 此时有：
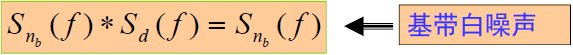
- 说明：
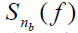的带宽没有被展宽。无数据调制时是噪声对回路影响最严重的情况。
- 总结：
- 由于延迟锁定鉴别器中存在非线性运算，即使输入噪声是高斯噪声，输出端噪声也将是非高斯型。
- 但是，若考虑到延迟锁定鉴别器后面回路滤波器的通带很窄，根据中心极限定理，回路滤波器输出端噪声的概率密度可以近似认为是高斯型。
- 因此，可认为延迟锁定鉴别器输出端噪声是功率谱密度等于零频率处噪声功率值的高斯白噪声。
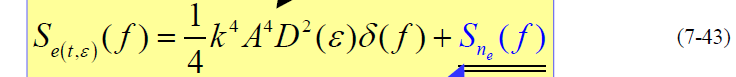
- 第一项：环路跟踪误差信号分量
- 第二项：噪声分量（高斯白噪声）
- 包络相关同步跟踪回路的等效电路模型
- VCO方程为：
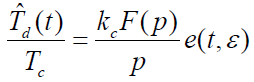
- 式中,
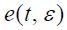是延迟锁定鉴别器输出跟踪误差信号分量与噪声分量之和。- 由于
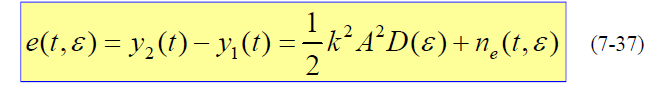
- 则有
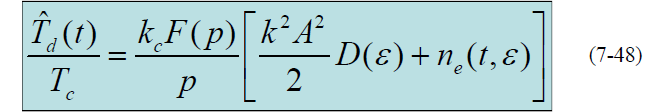
- 其中噪声
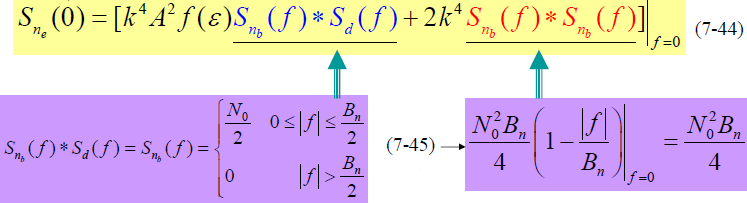
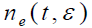的功率谱密度：- 由于延迟锁定鉴别器输出噪声可认为是高斯白噪声，功率谱密度是 (7-44) 式在零频率处的值。
- 令噪声双边谱密度是
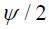。在没有数据调制情况下有：（影响最大情况）
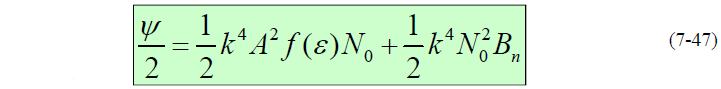
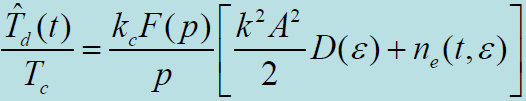
- 非线性等效电路模型：
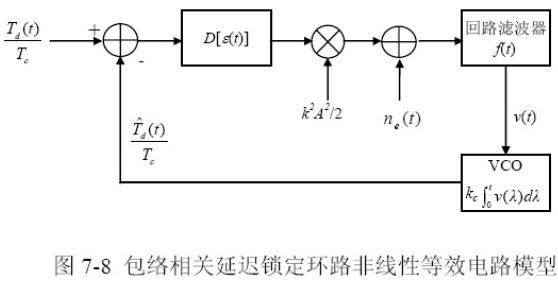
- 当环路锁定时，
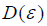处于正常工作区域，则有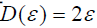
- 线性等效电路模型：
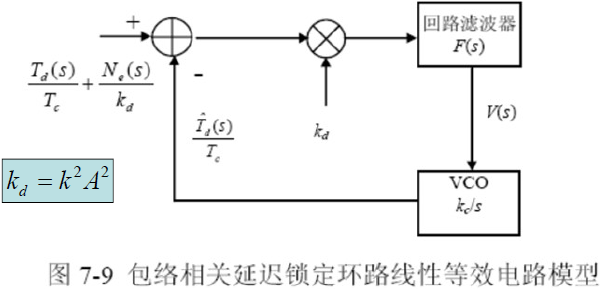
- 闭环传输函数：
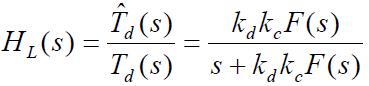
- 跟踪误差：
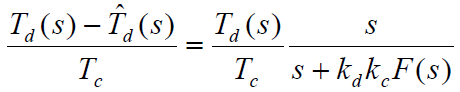
- 回路双边等效噪声带宽：
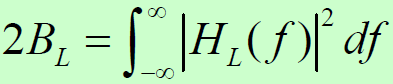
- 输入噪声功率谱密度在
内可近似认为是常数，其值为
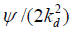此时均方跟踪抖动为：
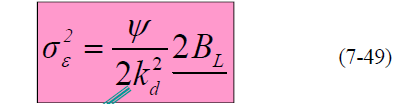
- 当跟踪误差ε较小时，
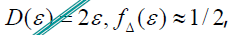，线性等效电路输入的噪声功率谱密度为：
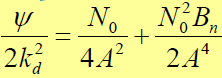
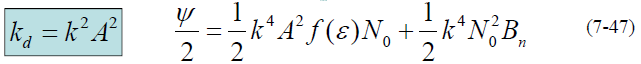
- 带入得：
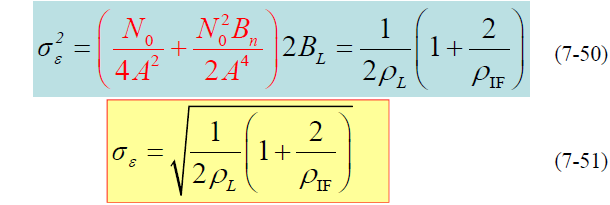
- 其中：
- 性能分析：
- 基带相关同步跟踪回路的跟踪抖动：
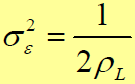
- 包络相关同步跟踪回路的跟踪抖动：
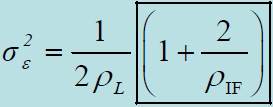
结论：
问题提出：
- 包络相关同步跟踪回路存在延迟锁定鉴别器中两相关支路必须精确平衡与电路较复杂的问题。
- 延迟锁定鉴别器中超前与滞后相关支路不平衡将引起鉴别特性曲线的失配。
- 为克服上述缺点，可以采用时分单相关支路的 τ-抖动非相干同步跟踪回路。
- 它具有结构简单的特点。
τ-抖动同步跟踪回路，简称τ -抖动环(Tau-Dither Loop，TDL)，除了延迟锁定鉴别器外，此回路与前面所给出的包络相关同步跟踪回路完全一样。
7.4.1 τ-抖动同步跟踪回路的组成及等效电路
回路结构：
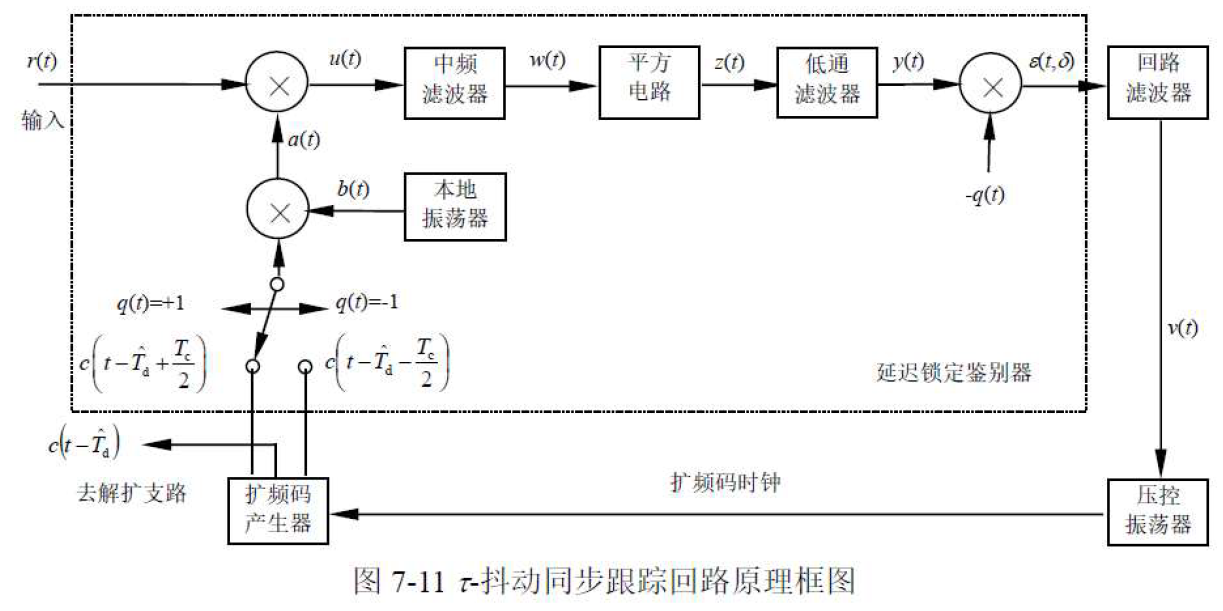
- 性能分析：
- 基带相关同步跟踪回路的跟踪抖动
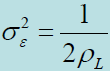
- 包络相关同步跟踪回路的跟踪抖动
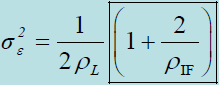
- τ-抖动同步跟踪回路的跟踪抖动
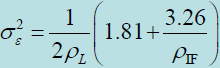
结论
(Double Dither Loop，DDL，双抖动环)是在双相关支路包络相关同步跟踪回路与τ-抖动同步跟踪回路基础上提出的。
既解决了双相关支路包络相关同步跟踪回路中两支路增益不平衡的问题，又解决了τ-抖动同步跟踪回路噪声性能变坏的问题；缺点:电路复杂。
双抖动环特点：
- 双抖动环的延迟锁定鉴别器与双相关支路包络相关同步跟踪回路基本相同
- 所不同的是利用开关函数使超前与滞后相关运算轮流使用两个相关支路
- 差值信号中由两个支路增益不平衡造成的影响就可相互抵消
若开关函数引起的瞬变效应可以忽略，则其性能与双相关支路包络相关同步跟踪回路的性能完全相同。
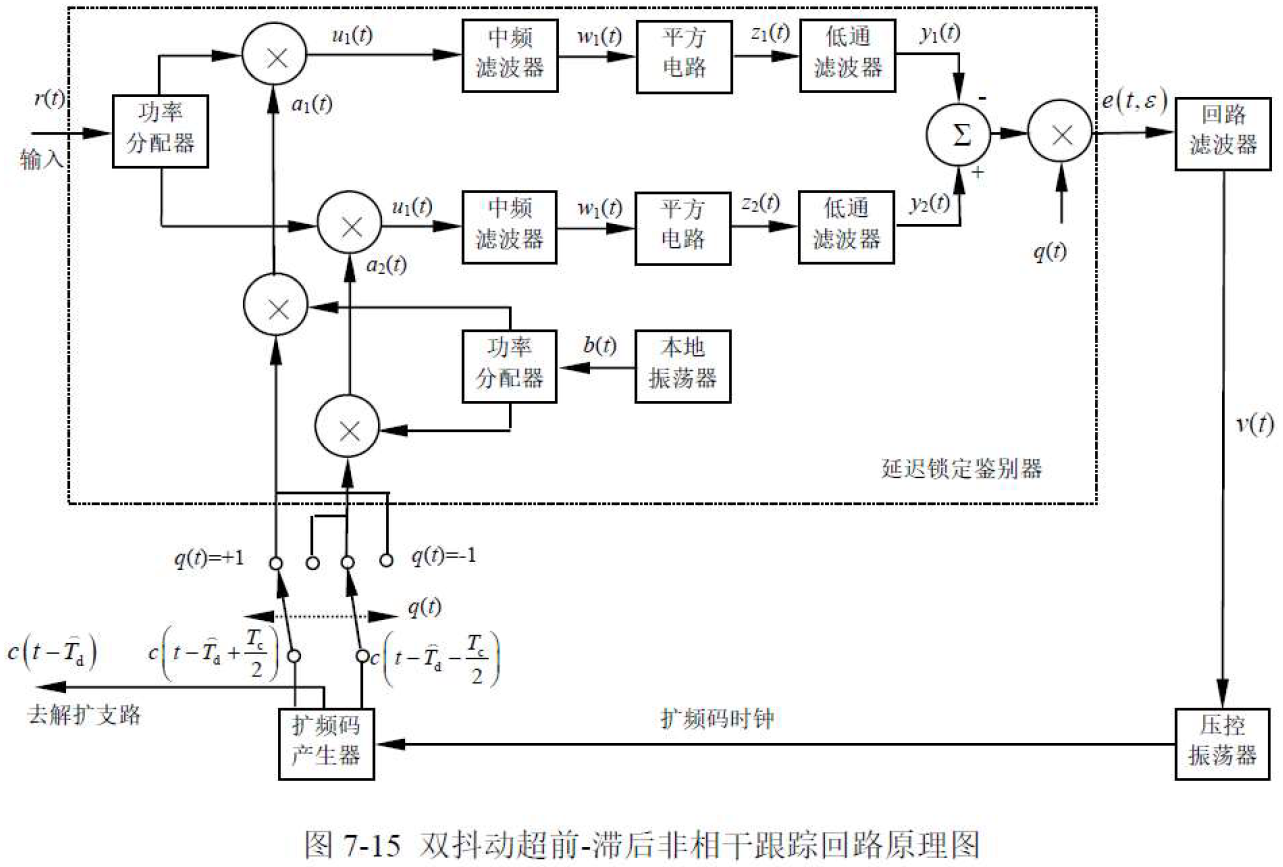
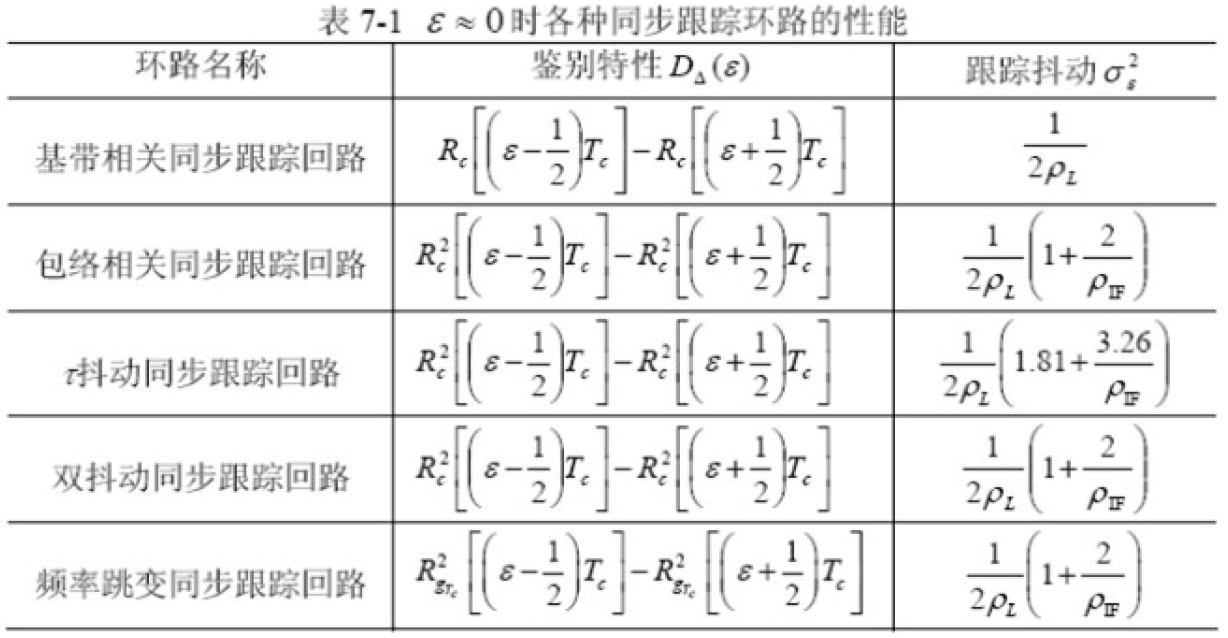
- 几种环路的鉴别特性和跟踪抖动性能
7.6 频率跳变系统同步跟踪
若有收获，就点个赞吧
0 人点赞
