OpenPose_2017CVPR

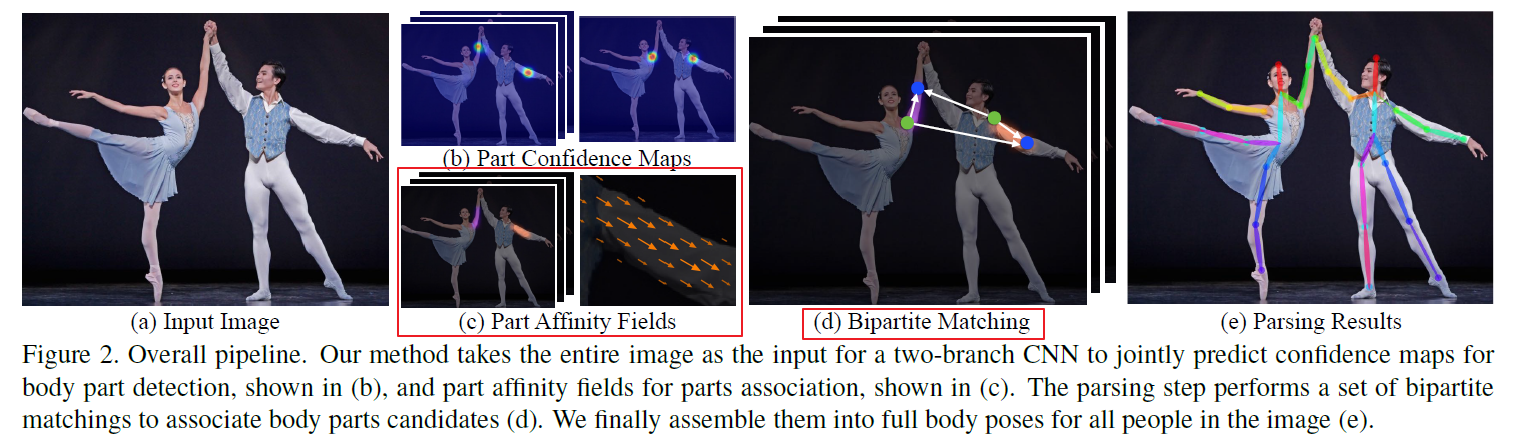
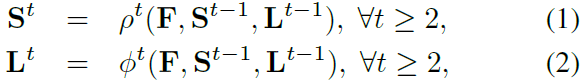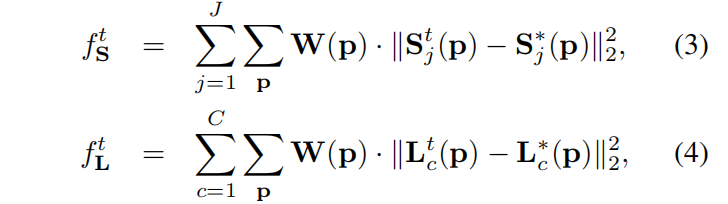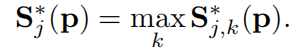《Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields》 openpose论文笔记

单词

Affinity:              关联
anatomical：           解剖

综述

top-bottom

缺点：

• 精度来自有人体检测；
• 重复计算，相对来说更耗时间；

优点：

• 精度相对更高；

  bottom-up

  缺点：

• 精度相对较低；

优点：

• 没有重复计算，处理时间和图片中人体解耦；

  方法

  

  思想

  利用双分支实现以下目标：

• 生成每个关节点的热力图（当然不是每个关键点单独一张图，每张图包括同一类型的关键点）；

  • 其实换个方式思考，如果真的是每个关键的都生产一张图的话，那么网络是无法提前预知到底有多少个关键点的，也即无法用固定的输出规模实现关键点预测输出！
• 生成关节点之间的关联度向量场；

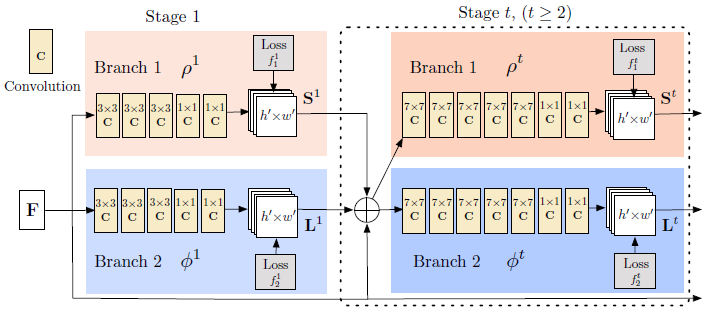
将其用公式表示即：
对于大小的图片作为输入，首先在branch 1产生一组2D的confidence maps ，对任意，有（其实S也即是通常所说的关键点热力图）；与此同时在branch 2会产生个向量域，也即每个肢体（关键点对）一个，并且对于任意属于的元素*（编码的属于肢体部位每个像素点方向向量，包括的x,y两个分量）；最后综合进行后续阶段的信息提取，每个后续阶段都会进行中间监督，避免梯度消失等情况。

细节

• 首先图片通过卷积网络（利用VGG-19的前10层进行初始化）进行处理之后获取feature maps ；
• 被输入stage 1的CNN网络中获取confidence maps 以及PAFS；
• 在接下来的stage中，前一阶段的两个预测以及原始图片的特征，将被连接用于产生精炼的预测；（下图展示了不同级中的效果）
  • 

• 每一级最后都有两个Loss 函数（每个branch一个）；（Loss采用L2 Loss -> 利用L2范数来定义偏差）
  

  • 
  • 其中：
    • 是confidence maps的ground truth；
    • 是PAFs的ground truth；
    • 是binary mask，其目的是为了解决数据集中，没有标注全的问题。当没有标注，，从而避免惩罚正确的预测；

      产生confidence maps

      利用标注了关键点的数据集产生，也即是通常所说的热力图；

• 每个confidence map是一个2D的关于关键点出现在特定pixel的概率；

• 设表示的是第k个人的第j个关键点的confidence map的ground truth，表示关键的位置的ground truth，则对于每个位置，其在中的值为（高斯分布）：

    ![image.png](https://cdn.nlark.com/yuque/0/2020/png/1480208/1595602735632-26eee42c-67e6-4a1e-877a-1683afd263cc.png#align=left&display=inline&height=40&margin=%5Bobject%20Object%5D&name=image.png&originHeight=79&originWidth=414&size=11346&status=done&style=none&width=207)

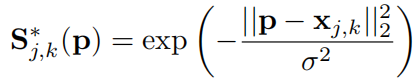
• 当然由于有多个人，所以同一类的关键点可能存在多个：

  • 
  • 公式表示的意思就是，对于第j类关键点的confidence map上每个位置的值，取不同人在该类关键点结果的最大值。
  • 
  • 这样一张图中就存在多个峰值！每个峰值对应一个关键点的具体坐标！

    产生PAFS

    PAFS主要是为了解决关键点连接（组合）的问题。
    

    关键点连接的基础是关键点对的连接，事实上，我们在预测第j个confidence map的时候已经知道了关键点的类别，也即已经包括了关键点在人体中所对应的位置，当然我们根据人体结构就能够知道需要将哪些关键点对进行连接。如果人体比较稀疏，那么我们完全可以按照关键点之间的距离进行聚类操作。此方法的弊端：人比较密集时，则无法区分。

作者认为，一种解决方法是：检测一个limb两个节点之间的中继节点，并检查它在候选部件检测之间的发生率。

这里中心的点归属也是一个问题，正如Figure 5(b)所示，有了中点那么如何确定中心点属于哪一对关键点呢？首先思考如果单纯用距离可还行？事实上，考虑到人的尺寸的不同，这个方法存在极大的限制。当然，一个显然的想法，如果在前期的检测网络同时输出人体检测框的位置信息，是否可以借助人体检测框来辅助关键点的连接呢？

中间点方法的弊端（人多的时候）：

1. 它只编码了位置信息，没有方向信息（没有方向也就导致出现Figure 5(b)中的绿色连线）；
2. 它将一个肢体的支撑区域减少到一个点（一个区域只包括了一个中心单点辅助信息）；

为了解决这个问题，本文首创PAFS，它既保留了肢体区域的位置信息也保留了方向信息！其核心是一个二维的向量场。
身体组成通过关键点对被分为个肢体，对于每个肢体都将生成一个PAF，同一类的肢体将在同一张图中生成。对于属于该肢体上的像素点，2D向量场将编码该肢体上从一个节点指向另一个节点的方向（指向问题，当然可以借助人体结构实现）。

也即是说，属于该肢体（就是有位于关键点对之间的部分，比如：脚到膝盖）的所有像素点将会编码相同的向量值。这就对应解决了中间点的两个弊端！但是，真的需要方向吗？如果已经能够确定一个肢体了，我们只需要找到肢体的首尾即可确定对应的关键点了啊！

假设一个肢体对应的两个关键点为：和，其中k表示第k个人，j表示关键点标记。如果像素点在肢体上，那么的值将是一个从点指向的单位向量；否则的话其值为0。

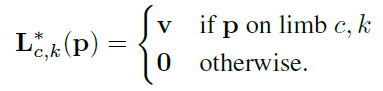
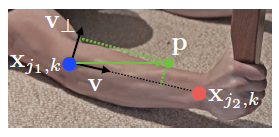
其中，。那么如何确定一个点是否在某个肢体上呢？事实上无需精确定义，只需要确定一个矩形区域即可（当然这是用于产生训练集的label而用，训练之后网络会自己判断出）：

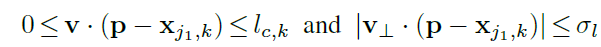
其中的，根据具体情况而定（人工标注罗！）
如果某个像素点在多个同类肢体上，其值为各个同类肢体在该像素点值的平均值：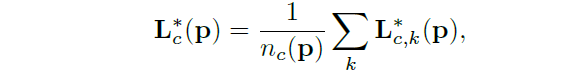

其中的也即代表了该像素点所在同类肢体上的个数。

为何取平均值？平均值取后那么此处的方向性将会丢失？

测试阶段进行关键点匹配，采用连接两个点然后计算他们的线积分的方式。假设有两个点，通过沿着线段采样PAF测量两者连接的confidence：

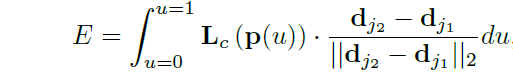
其中，表示之间的像素点，即：，实际在计算积分时采用的是针对u等间距抽样求和。

利用PAFS解析多人

对于检测的confidence map，利用非极大值抑制（除此的非极大值抑制，是综合了关键点连接信息之后的非极大值抑制），从而获取离散的关键点候选集合。公式表示如下：
设获取的所有关键点候选者集合为，其中的表示的是在图片中的位置坐标。对于这些点需要找到对应的点组成肢体（关键点对）。定义变量表征两个关键点是否连接，我们要做的是找到最优的所有连接：
如果我们考虑单独的一对匹配（也就是说考虑多个肢体中的其中一个），那么该问题就转化为maximum weight bipartite graph matching problem。当然连接的方式存在多种，如Figure 5(a)所示，他们一起组成一张图，节点就是所有的关键点候选值，边即是两类关键点之间可能的所有连接，边的权重利用之前的线性积分求得。bipartite graph中的一个匹配就是原图边的一个子集，在子集中任意两条不同的边没有公共节点。也就是说我们的目标是：1、得到bipartite graph的一个匹配；2、该匹配具有最大的边权重，即：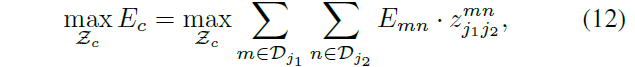

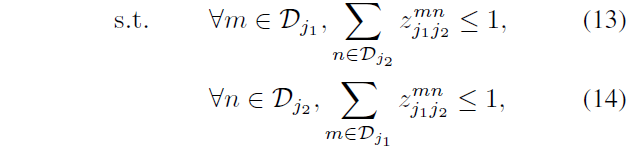
公式13,14论文中是为了使得没有两条边共享一个节点，因为求和值按照定义只能是0或者1，也即是说每个点最多存在一个点与之匹配 -> 可能存在不被匹配的点。我觉得这种方式的话，事实上关键点匹配的过程也即是对关键点所属关系的确定。

论文指出为了解决点多的问题，采取了两种方式进行优化：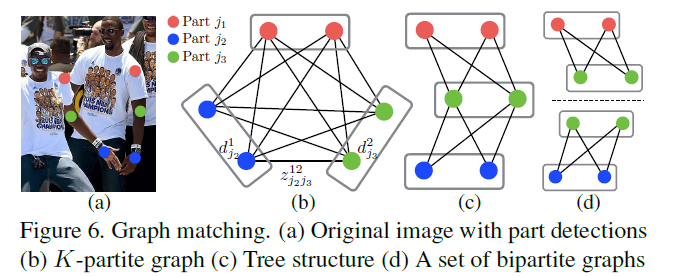

1. 利用人体本身的结构信息简化NP问题，也即是论文中提到的：我们选择最小的边数来获得一个生成树骨架的人体姿态，而不是使用完整的图（对比Figure 6(b)(c)）；
2. 将匹配问题分解为bipartite matching subproblems，也即是对比Figure 6(c)(d)；
   • 其最终对应整体的优化：

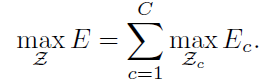
     事实上，上面的方法比较容易想到，将关键点的匹配分为临接关键点的匹配问题。但是最核心的还是如何很好的进行临接关键点的匹配 -> PAFs。 显然，这种将关键点匹配转为临接关键点的匹配问题也存在一个问题：每个小匹配上都获得了最优的解，但是在总体匹配上并非最优的。当然，这种情况相对来说概率比较低。 bottom-up的方法只有第一阶段需要用的CNN，第二阶段利用传统方式即可。