参考:自动求导 博客参考(英文,非常棒!):https://grzegorzgwardys.wordpress.com/2016/04/22/8/
微分算子
梯度
计算机求导方式
手动求导
数组导数
符号求导
先利用计算机求解导数表达式,然后利用表达式计算最终的导数值,和人计算过程类似;
没有用于深度学习求导原因:表达式冗长。(冗长在于未化简之前,并且这样看起来也相对复杂)
自动求导
前向传播
采用计算图的方式;首先表达式生成图: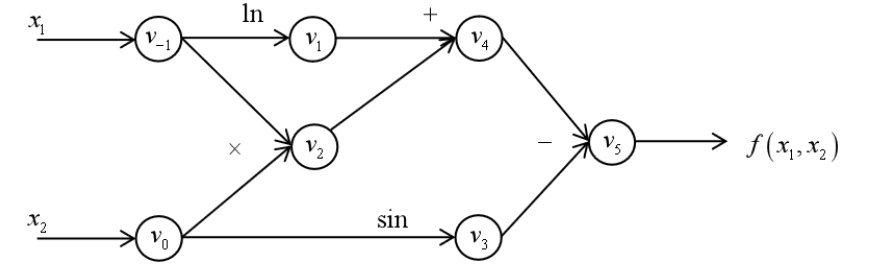
利用图以及链式法则进行导数求值:(基础函数导数公式还是必须的)
从上面可以看到,只要有了计算图以及基础函数的求导公式,那么进行一次前向传播即可得到每个中间函数关于输入变量的导数;
反向传播
反向传播和前向传播不同,它是计算输出对于每一个中间变量的导数(深度学习参数更新需要用到的导数)
其和前向传播类似,需要先进行计算图的生成,然后利用链式法则,依次求取输出函数对于中间变量的导数。
对于上面的计算图,反向传播可以计算出: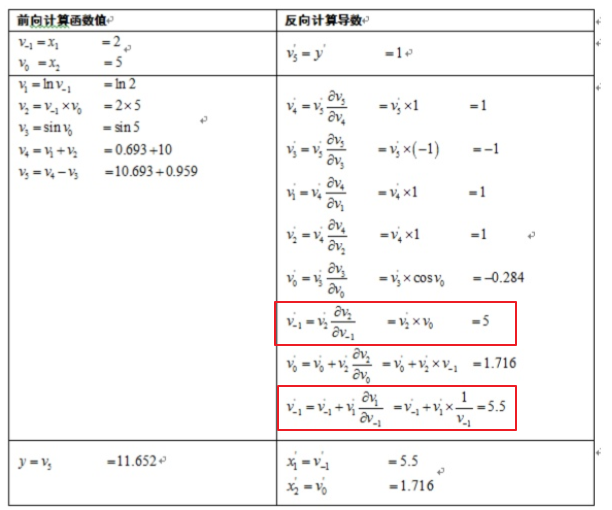
框出导数出现两次是因为,该后面有两个节点:
BP算法中有两类导数,一类是节点导数,一类是参数导数。计算参数的导数是最终的目标,节点导数是中介。
矩阵求导
矩阵求导可参考:
矩阵求导术
计算机中,通常就是矩阵运算,函数y对多个自变量进行求导可以采用矩阵求导的公式。
CNN求导
CNN-tutotial
CNN虽然被称为卷积,但是更类似于相关运算:其中
为卷积核大小除2取整,但是相关运算可以当做卷积来处理(将卷积核绕核中心点旋转即可)。基于此可以将CNN的卷积运算写作更简单的形式:
- 卷积中的下标
表示了平移的长度;注意同一个函数表示可以不同,比如
都是表示同一个函数,知识自变量形式不同(变量替换,形式替换)。有时候可能会被迷惑!
- 还有就是
,
也表示相同的函数;只是
既可以表示具体位于
的值,又可以表示整个函数!

