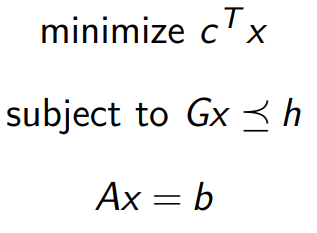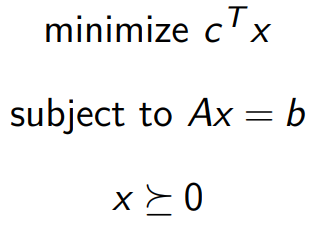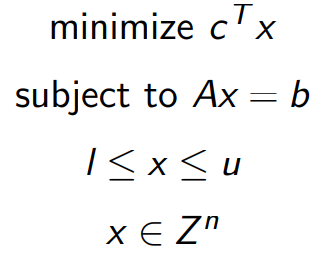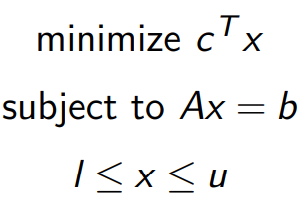常见优化问题形式：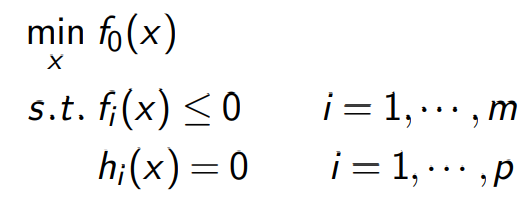

其中：

• 是优化变量，通常是一个向量
• 是优化目标函数
• 是不等式约束
• 是等式约束

事实上绝大多数的优化问题都是很难甚至无法解的，我们主要讨论易于处理的优化问题：线性优化、凸优化以及随机优化。对于其他难以优化的问题，我们可以采取合理的近似、变形等手段使其变为易于处理的优化问题。

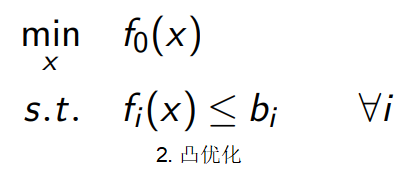
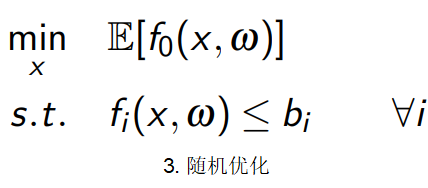
值得一提的是，易于处理的优化问题是有很多算法可以解决的。所以对于一个优化问题，我们最终的目的就是将其化为易于处理的优化问题形式，对于其具体的解我们是不太 care 的。

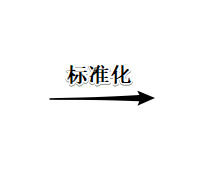
线性优化

问题形式

注：上式中，是以向量运算的形式展现出来的。

案例

如何将下式化为标准形：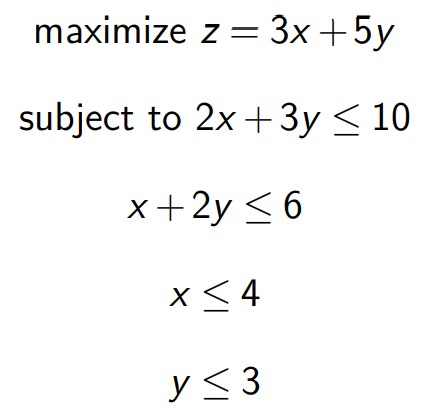

步骤如下：

1. 引入新变量将不等式约束变为等式约束

1. 通过分解变量为两正数相减的形式，将所有变量变为正数约束（本题中即为）

1. 将所有的变量进行替换之后即成为标准形

   几何作图法

   几何作图法适用于低维的优化问题，比如上题中的两个变量的问题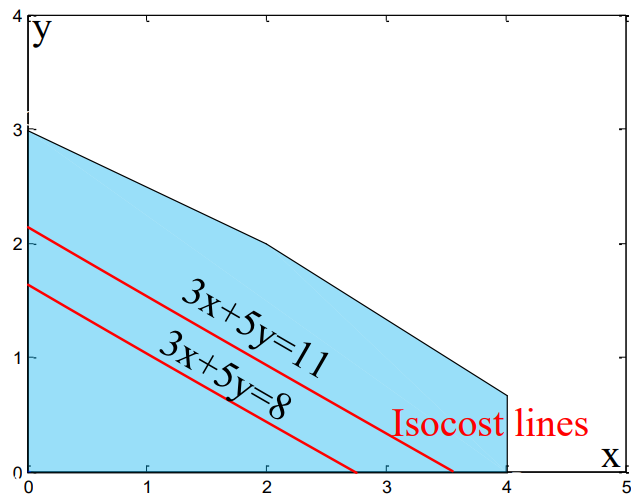
   
   通过几何作图法，我们可以发现，优化问题的解一定在极端点（Extreme Point）

   定义：位于多面体 中的点 ，如果在 中不存在两个非 点 使得 ，那么 则成为 中的极端点。 引理：Assume that a LP in standard form is feasible and the optimal objective value is finite. __There exists an optimal solution which is an extreme point.

Simplex法

对于高维情况，利用作图法是无法实现的。这时可以采用 Simplex Method, Interior-point Method, Cutting-plane Method等，此处介绍 Simplex Method。

• 其思想来源：根据最优解位于极端点的特性，采取合适的方法从一个极端点移到另一个极端点进行判断是否是最优点。
• 特点：非常高效，但是只能用于 LP 问题
• 核心内容：如何合理的限制极端点的搜索范围，使得结果更快被找出来（不用遍历所有极端点）

具体算法

博客参考：https://blog.csdn.net/weixin_40955254/article/details/85073962 https://blog.csdn.net/facetosea1/article/details/84699786
https://wiki.mbalib.com/wiki/%E5%8D%95%E7%BA%AF%E5%BD%A2%E6%B3%95

基变量：事实上就是被选做产生满秩矩阵的子矩阵系数对应的变量，每次迭代对基变量进行替换即可
上面第二个链接介绍了，比较详细的单纯形表解决线性规划的方式。

这里总结一下，博客中讲述的内容。将含有不等式约束的线性优化问题标准化之后，那么约束方程中只包括等式约束。假设等式约束包括 个，变量包括 个，如果可行域存在，那么一定有 ，当两者相等时没有讨论的必要，此时优化目标只能取一个值，所以这里讨论 的情况。 时，等式方程组的解空间自由度至少为 ，此处假设每个等式都是有效的，那么此时解空间自由度为 。根据线性代数里面的方法，我们可以将化为 -> => ，方程组的解空间自由度为 向量的长度。在单纯形法中，称为基变量， 称为非基变量。而优化目标函数通常都被转为非基变量的函数，即：，如果函数中 前面的系数都为负数（例如：，此时就是算法的出口），那么由于（ 是一个向量），所以 在 时取得极值。并且显然，从高维空间来看 一定是解空间的边界面，也即是说 ，解出来一定对应的是一个极端点。

上面讨论的时优化目标函数取最大值的情况。

如何实现基变量的替换呢？可以选择优化目标函数中变量前系数值最大的非基变量作为候选值，然后以一个包含该变量的方程为基准，在其它方程中（包括优化目标函数）消去该变量，如何选择基准方程呢？可以选择的值取最小值的方程，这样进行消去之后能够满足所有的 （https://zhuanlan.zhihu.com/p/259389525）

网络流问题

网络

即有向图（digraph），图由 个节点，以及 条有向边组成。

• 边可以表示为节点的有序对： 表示第 条边起点为
• 假设从节点 到节点 最多存在一条边
• 不存在自循环的边，即

边-节点关联矩阵： matrix with entries

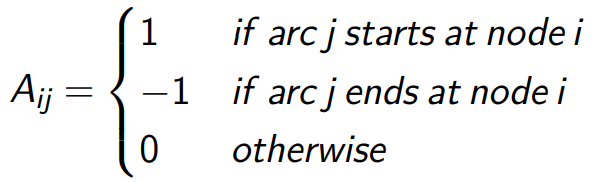
一个图的例子：（事实上不用这种表示也可以，只要能够表示节点和连接关系即可）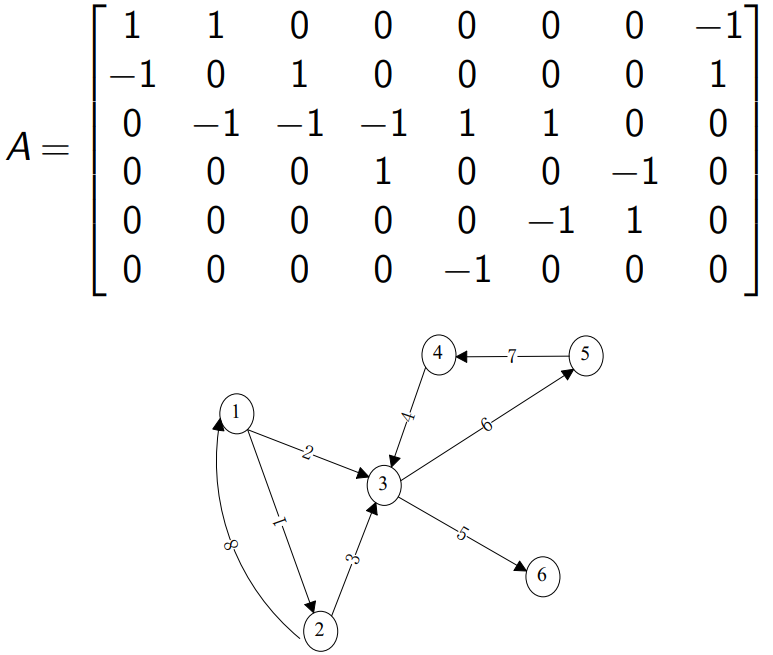

流向量

流向量 （ 条边，也就是表征了每条边上的流量情况）

外部供给

为所有节点注入外部流量，所以是 维向量

最小代价网络流问题

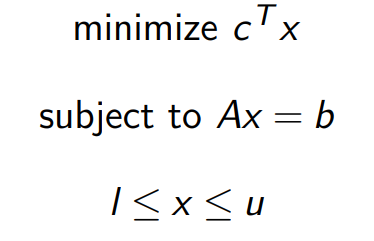
其中：

• 表示单位流量从边 通过产生的代价
• 表示边 上的流量限制，通常来说 （正负表示流量的方向）
• 假设 ，并容许

很多问题都是最小代价网络流问题的特殊形式，比如说

最大流问题

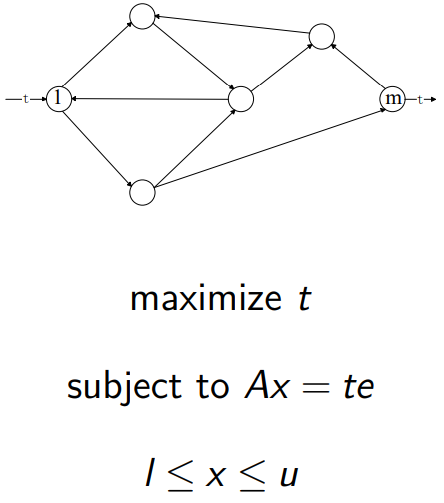
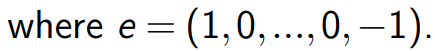
可以将其进行微小的变换：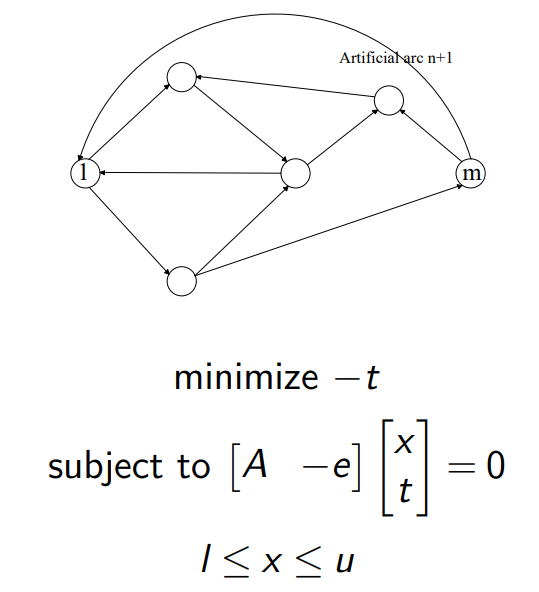

组合优化问题： 组合优化问题设计到，优化变量取离散值的情况，相对于连续问题来说更为复杂。往往采用将离散域扩充为连续域的方式（但是要证明两者等价，不能随意扩充）

最短路径问题

最短路径问题，我们是希望在节点 1 和 m 直接选择合适的路径，使得路径的长度最短。简单起见，假设所有路径单位流量的代价都为 1。可以将路径选择的问题转为流量的问题，即如果路径被选择，则该边上流量为1，不被选择则流量为0。所以和容易类别最小代价网络流问题，写出如下优化问题：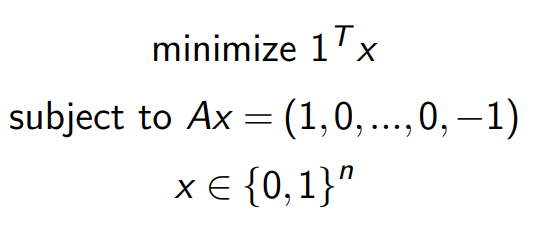

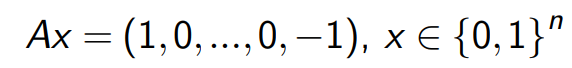
条件松弛之后得到标准形式：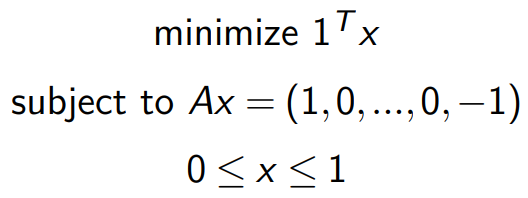

网络 Simplex Method

这就是为了解决网络流优化问题的算法。
Basic idea: Construct negative-cost cycles based on a spanning tree of the network graph.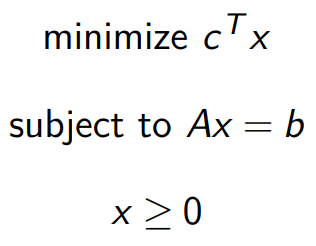

这里可以知道，非网络的线性优化问题，可以采用网络单纯形法，利用生成树的思想来解决问题（需要将原问题转为图描述的等价形式）。
网络单纯形法：找到一颗生成树，使得生成树的在给定输入流量的情况下有最小代价（就是前面所说的最小代价问题）

为何会想到生成树呢？？？

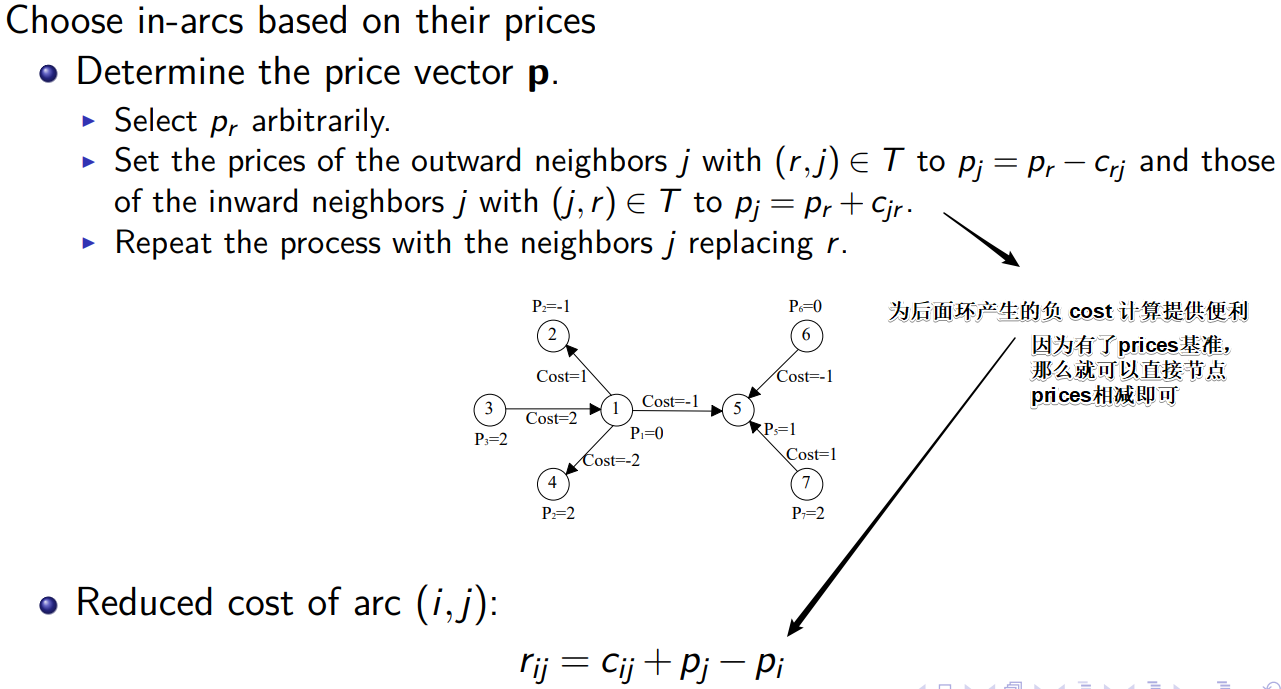
在后续，对环新增边增大流时，将会产生某些边流量为0的情况，这时候这些流量为 0 的边就可以被舍弃掉。舍弃的规则：舍弃之后的生成树为 Strongly Feasible Tree

A feasible tree with corresponding flow vector is said to be strongly feasible if every arc of with is oriented away from the root.

对于初始的 Strongly Feasible Tree 采用 Big-M Method。

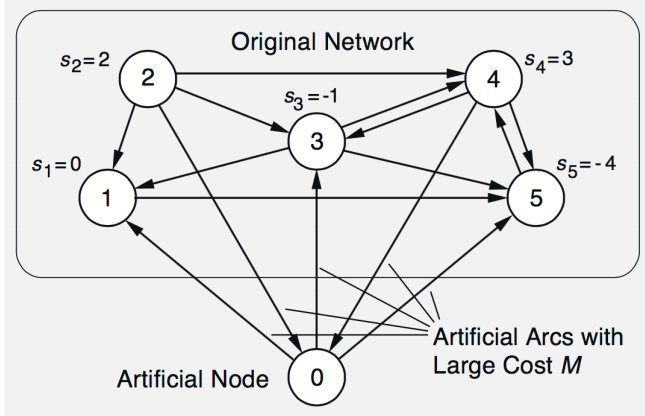
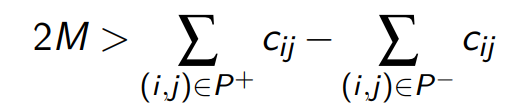
算法终止条件：