网络权值初始化

参考：
网络初始化

目的

防止不好的权值初始化造成梯度消失或者梯度爆炸，并且好的初始化能够加快收敛，当然好的初始化也同样可以提高准确率。

标准正态分布

分布是表示该层的所有神经元的数值分布，它们同时满足标准正态分布。
正态分布过程中，通常做法：

• 平均值为0，标准差为；
• 的取值很重要，太大太小都会产生问题。

解决办法：

• 每一层的都和输入的size相关（也即是扇入）；
• 利用size的大小来缩放；
• ；

  Xavier初始化

  扇入/扇出

  指的是神经元的个数；
  

  具体方法

  此方法提出时，主要针对像sigmoid、tanh这类的激活函数。（下图公式表示的时均匀分布）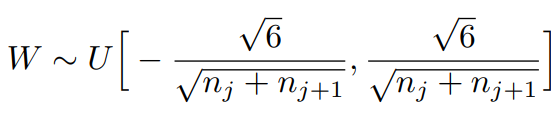
  
  其中：
  表示该层传入网络连接数（扇入）
  表示该层传出网络连接数（扇出）

  Kaiming初始化

  此方法对于Relu激活函数（非对称）非常有效。
  其方法：

1. 选择标准正态分布的数字填充权值矩阵；
2. 数组乘以（就是进行放缩）
   • 其中的n表示的传入网络连接数（扇入）

     初始化案例

     # 通常在model的__init__函数的末尾初始化权重（已经定义了modules)
     # init weights
     for m in self.modules():
     if isinstance(m, nn.Conv2d):
        nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
     elif isinstance(m, nn.BatchNorm2d):
        nn.init.constant_(m.weight, 1)
        nn.init.constant_(m.bias, 0)