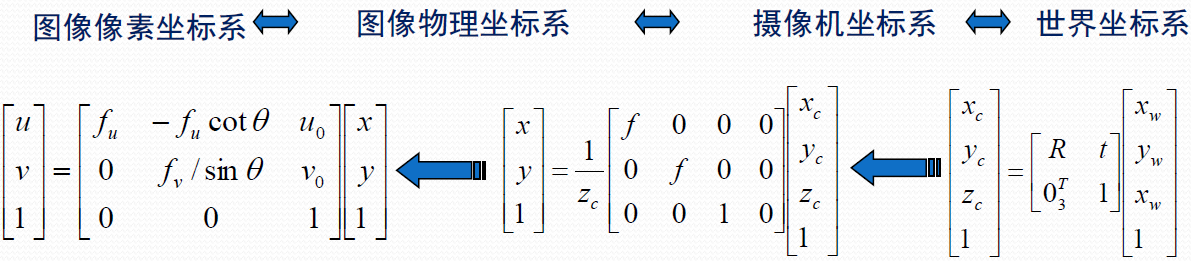
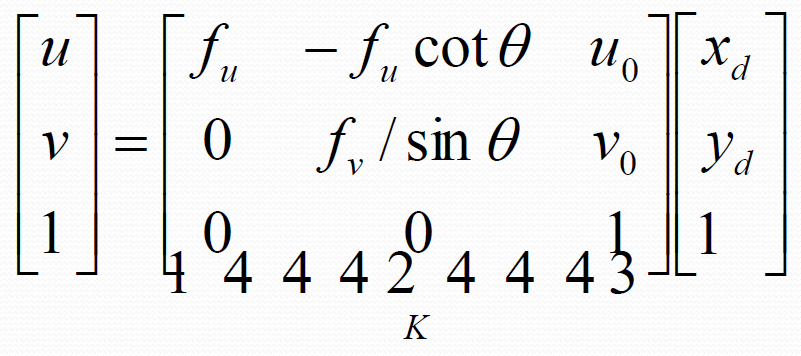图像转换过程
- 凸透镜成像
- CCD,CMOS等感光,根据光强的大小产生对应大小的电信号(包括了成像平面的采样过程)
- 彩色图像需要RGB三种颜色的色块网格,实现对三基色强度提取;

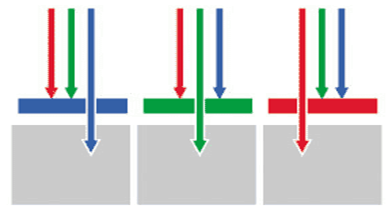
- 如果没有色块网格,那么将会得到灰度图(灰度图每个像素值表示了该位置处的光照强度)
- 彩色图转灰度图(大概公式):
- 将对应的电信号后续处理即可得到彩色图像(RGB格式)
- 这里有一个问题:如果将世界坐标系和相机坐标系重合(两者都能表示世界空间,都是连续的),这样世界坐标系就可以利用相机坐标系代替了,为啥还需要世界坐标系呢?
对于单张图像的确如此,单张图像的分析,完全可以以相机坐标系为世界坐标系。但是如果需要进行一些更复杂的任务,例如多视角三维重建。那么我们就需要世界空间的一个固定基准,来完成坐标之间的对应转换关系。
如果要更详细的过程,可以参考下面这张图:
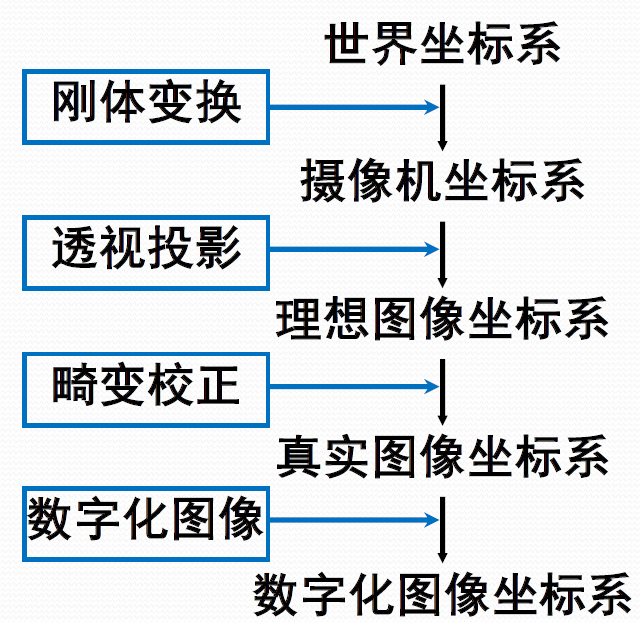
其中的刚体变换,包括一个旋转和平移过程。
透视投影(透镜成像)
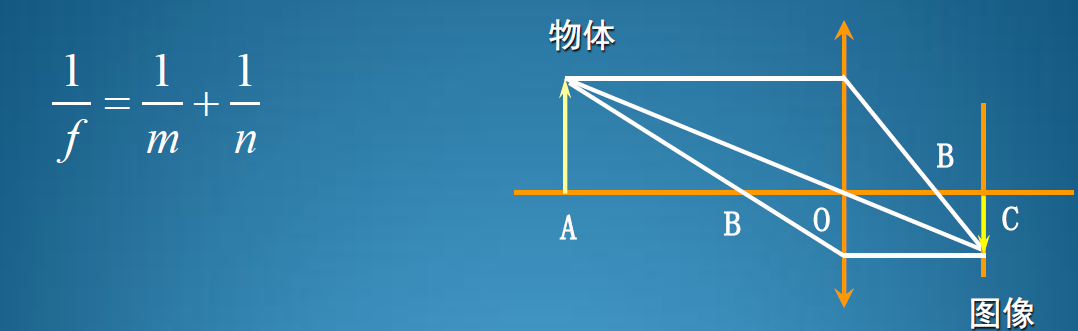
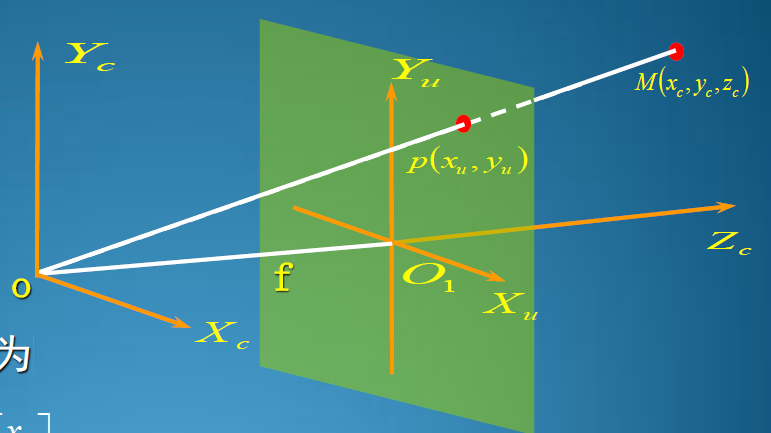
相机坐标系坐标原点即透镜中心,成像平面在透镜后面;但是这个过程等价于成像平面在透镜前面(如下图所示)而大多数情况下,都是采用后者来表示。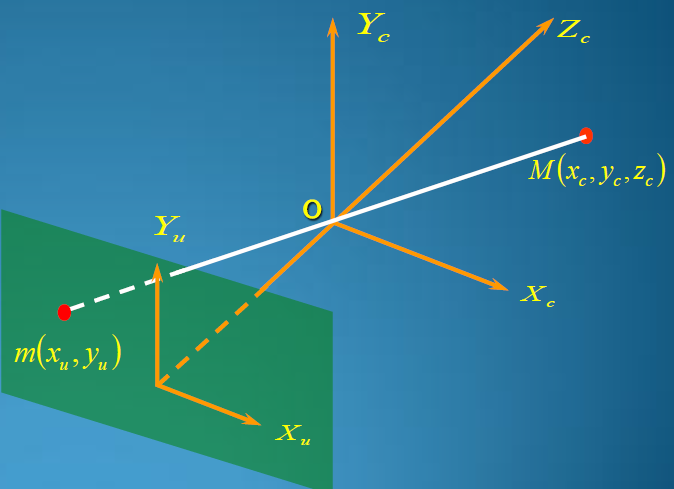
采用后者表示的优势是,参数矩阵中的负号可以去掉,公式如下图所示。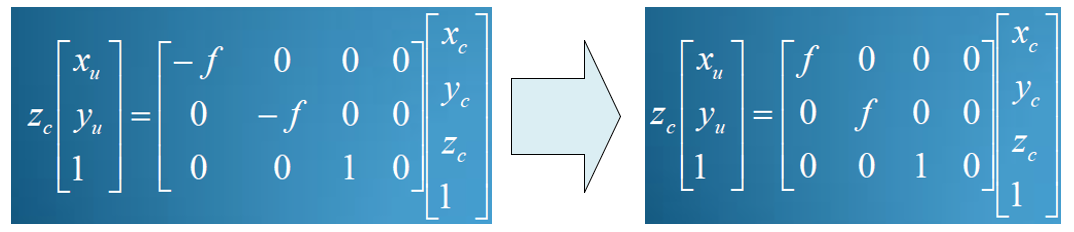
图像畸变
图像畸变有两种形式:径向畸变 & 切向畸变。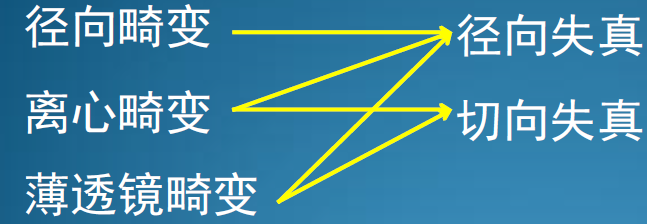
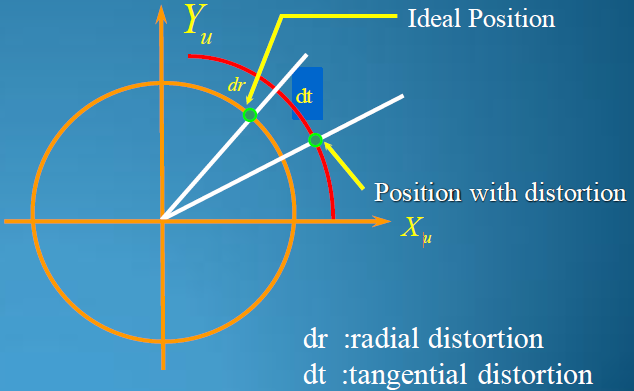
畸变原因:1、成像模型并非小孔模型,透镜本身会造成成像的失真(理想透镜中心放大率和边缘并非相同);2、透镜存在误差;
畸变是光学透镜的固有特性,不能完全去除,通常情况下,畸变程度受到透镜参数以及传感器参数的影响。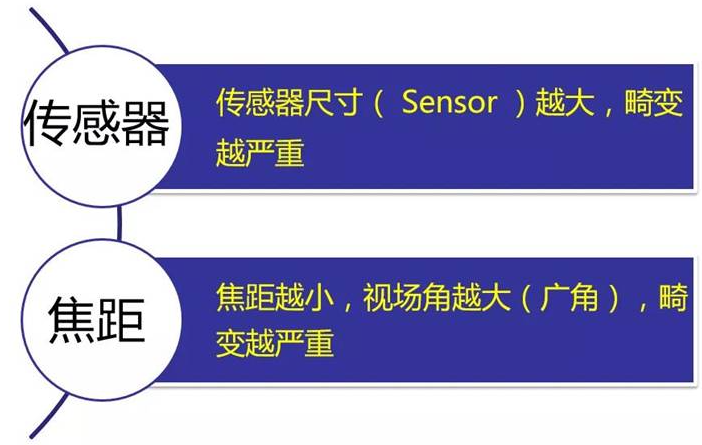
图像数字化
下面这张图考虑的图像坐标系更具有普遍性,并非正交的坐标系(两个基之间存在一定的夹角)。(但是通常来说,图像坐标系是正交坐标系)
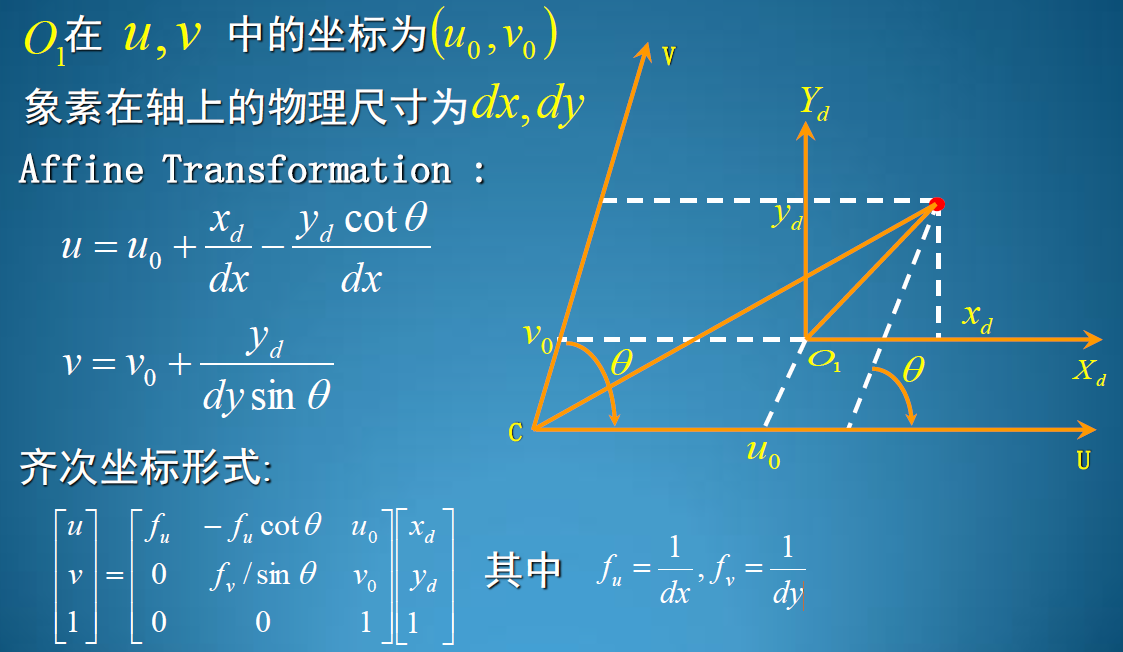
理解公式:将原来正交坐标系的点,对应到非正交坐标系即可。(注意坐标系下坐标的含义 => 必须平行坐标轴得到坐标分量)
线性摄像机成像模型