传统光流算法

计算机视觉—光流法(optical flow)简介 【文献综述】光流法的过去，现在和发展趋势

离散差分

在连续函数中，我们可以利用连续函数的求导定义进行求导：，这个定义非常好理解。但是，当我们遇到离散数据时，比如一张图片数据，我们如何表征该函数对于的导数呢？
通常做法是利用差分：同理，对于求导（此处是前向差分）。对比两个定义，其差别在于：导数是考虑自变量变换无穷小的情况下，但是差分是自变量变化为1。
我之前还在纠结什么单位啥的？感觉懵逼了。事实上差分可以看做是导师的一个近似罗，当然差分也可以看做是微分的近似（）。也就是说，看该公式的角度不同可以产生不同的结果。

1. 变量单位不同，连续函数变量可以是距离，但是离散的不可能是距离；（错误！都同样表示的是距离，即使用表示也一样，同样可以看做是距离啊！）
2. 含义不同，连续的导数反应了函数变换的快慢，差分只能反应相邻单位的差异；（错误！差异在一定程度上，也能反映函数变换的快慢，差分是导数的一个近似而已）

我用单位来思考就有点奇葩了，思考得不对！单位其实并没有被体现啊！

值得一提的是，在二维图像数据中，的单位并非物理上的米，毫米等，其以像素为单位。在差分式中，分子为1，而1总是给人的很大的感觉（但是什么又叫小呢？肯定是需要参照对比的）。物理问题向纯数学转换，首先需要注意单位，但是单位完全可以是自己选择的，不同的单位对于不同的尺度。当然，不代表尺度越小的单位下，差分式的误差越小。虽然在物理意义下，小单位选择貌似差分式更接近于导数极限，但是它们都是在距离为单位1的条件下差分的，没有优劣（1就是1）。
距离为单位1的差分仿佛误差很大，但是还是需要根据具体情况而定，我们只需要保证在误差范围内的适用性即可。
通常情况下，关于离散函数的关系式推导，我们都是先假设函数连续，然后按照连续函数的方式来推导，最终的结果当然还是要转回离散的情况。

前提假设

1. 相邻帧之间同一目标的亮度恒定；
2. 相邻视频帧的取帧时间连续，或者，相邻帧之间物体的运动比较“微小”；（即需要满足：时间的变化不会引起空间位置的剧烈变换，换句话说也即是：不能太大）

   小运动的原因：减小误差。也即是说大运动的误差更大。试想，在相邻帧之间时间间隔为，那么产生很大的，那么显然导数利用差分表示时误差就更大了。当然最小的极限也只能是单位1了！ 那么什么才算小运动，根据后面的叙述可知，移动之后前后的领域窗口相交！

事实上在计算机中图像都是按照数组的形式存在，不可能在上连续，在这种情况下，微分近似利用差分替代。（当然连续情况下的导数同样利用差分替代，**替代的原因以及误差没有想明白？— 误差在接受范围内**）

光流概念

“光流（optical flow）是空间运动物体在观察成像平面上的像素运动的瞬时速度。”
光流法是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法。
对于光流的研究通常基于灰度图。
一言以概之：所谓光流就是**瞬时速率，在时间间隔很小（比如视频的连续前后两帧之间）时，也等同于目标点的位移。**

光流物体意义

一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动所产生的。
当人的眼睛观察运动物体时，物体的景象在人眼的视网膜上形成一系列连续变化的图像，这一系列连续变化的信息不断“流过”视网膜（即图像平面），好像一种光的“流”，故称之为光流。光流表达了图像的变化，由于它包含了目标运动的信息，因此可被观察者用来确定目标的运动情况。

显然，根据光流的定义，其能够很好的描述运动的物体，从而去除背景干扰等，但是相机的移动确实是一个需要解决的问题。

光流场

场指物体在空间中的分布情况。场是用空间位置函数来表征的。
向量场（也叫做矢量场，vector field）是由一个向量对应另一个向量的函数。
标量场（scalar field）是由一个向量对应一个标量的函数。
显然，光流场是一个矢量场，它反映了图像上每一点灰度的变化趋势，可看成是带有灰度的像素点在图像平面上运动而产生的瞬时速度场。它包含的信息即是各像点的瞬时运动速度矢量信息。

基本约束方程

设表示某一对象在时刻其位于坐标处的像素灰度值（是否必须是灰度？应该和亮度相关），假设在时间时刻前面所述位于坐标像素点移动了（这里运用了假设2），那么根据假设1可知：

该式按照泰勒展开有：

故有：


当然，根据原数据就可以得到（在假设2的条件下，能够得到上述等式，但是事实上，图像数据是离
散的，I_x, I_y等利用离散的导数替代，离散导数与之差异……），在此处可以看作常数。我们只需要求得即可，它们构成光流矢量。
显然一个等式不可能解出两个未知数，此时需要引入另外的约束条件，从不同的角度引入约束条件，导致了不同光流场计算方法。按照理论基础与数学方法的区别把它们分成四种：基于梯度（微分）的方法、基于匹配的方法、基于能量（频率）的方法、基于相位的方法和神经动力学方法。（除了根据原理的不同来区分光流法外，还可以根据所形成的光流场中二维矢量的疏密程度将光流法分为稠密光流与稀疏光流两种。）

Lucas-Kanade(LK)光流法

LK在前面两个假设的前提下引入了假设3：

• 保持空间一致性；即，同一子图像的像素点具有相同的运动（速度大小和方向相同）。（将物体简化为刚体）

  也可以说是，相邻像素具有相似行动，例如量化之后：在目标像素周围m×m的区域内，每个像素均拥有相同的光流矢量。

我们对区域中的个点进行考察，显然对于任意有如下等式：

个方程有：



利用最小二乘法，即要求，也即是，令, 关于求导得到:,显然取极小值时有:
通过结合几个邻近像素点的信息，LK光流法通常能够消除光流方程里的多义性。而且，与逐点计算的方法相
比，LK方法对图像噪声不敏感。

LK光流算法实现

后续补充

金字塔LK光流法

由于LK约束条件比较严格, 在条件不满足条件下误差较大. 比如其中的小运动. 当物体运动很快时, 就会产生较大的误差. 如何解决这个问题呢? 将图片进行缩小. 原本[M, N]大小的图片上, 目标位移为[U, V], 那么图片缩小为原来的后, 位移也缩小为原来的, 只要足够大, 那么原来的大运动也会变为小运动. 从而KL光流法再次适用.

金字塔LK论文

问题陈述

假设有两张图片:, 表示的是在位置处的图像灰度值, 表示的是图像在像素级坐标下的位置, 并假设图像长宽为: . 当然都是离散的函数(为了后续推到, 需要假设其为连续函数).
现在需要解决的问题是, 第一张图像在位置处的点, 如何在第二张图像中找到一个与之最为相似的点, 当然, 根据离散的特性唯一可以被看作是所研究像素点的速度. 同样,也即是光流. 的定义为将以下表达式最小化的:

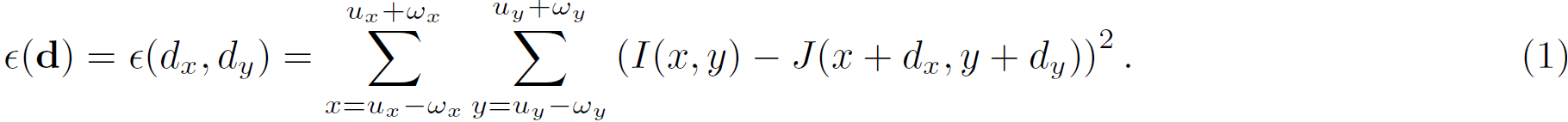
事实上，这个等式和前面讨论LK光流法中的约束是等价的，只是形式有些差异！之前的最小二乘法与此处的最相似相契合。

从公式中可以看到, 该残差是在一个邻域进行衡量的, 其大小为: , 其中取值为整数.

图像金字塔

记为第0级图像, 其也是分辨率最高的图像, 长宽为, 对于后面更高级的图像, 其分辨率将会被降。即：，更高级的图像定义如下：

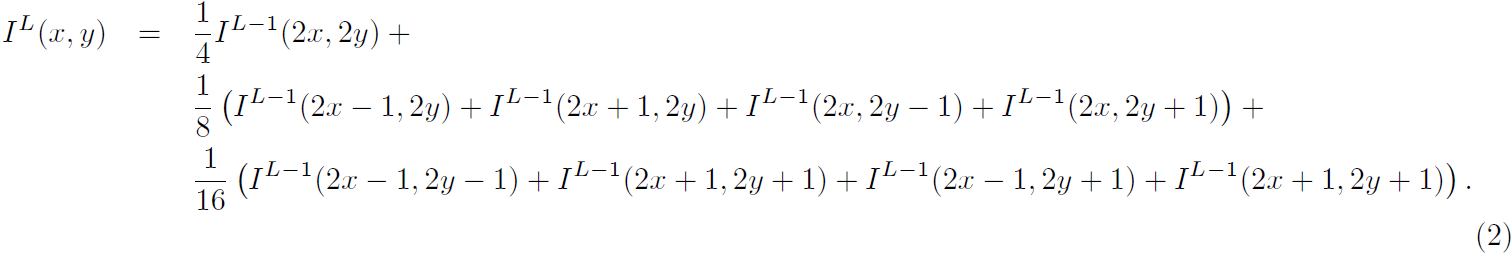
为了解决的情况需要给原图添加一个额外像素圈：

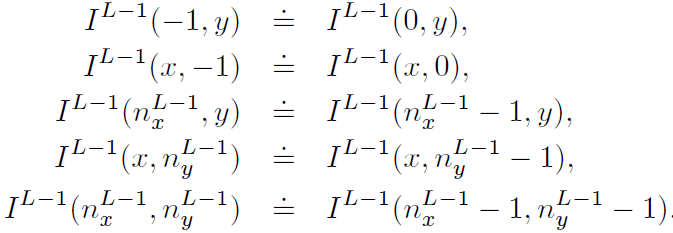
这样，就有：，那么第级的长宽满足：
，即：（满足该不等式的最大正整数）。
根据以上的原则就可以构造两张图像的金字塔表示：，通常来说不会大于4。多层的目的是将大运动（运动大于邻域窗口）化为小运动。
值得注意的是，公式2可以看做是，图像先进行低通滤波，然后进行下采样（这相当于CNN中padding为1，步长为2的卷积操作），低通滤波器为：，当然也可以选取更大的滤波器。

滤波器的作用是使得图像更平滑，直接采样可能会使得相邻像素之间的较大差异。

金字塔特征跟踪

特征跟踪的目标是：对于图像中一个给定的点，在图像中找到其位置。对于中的点，经过级金字塔之后，其位置记为：，根据之前公式知道：

金字塔结构计算流程如下：

• 首先，计算最深一层(层)图像（像素最低）的光流；（利用LK算法，或者利用定义的最相似约束等式）
• 然后，将深层的光流向浅层传播，作为浅层光流的的初始化猜想值，基于初始化猜想值计算出更精确的浅层光流值。

现在讨论和层更数学的关系：
假设在层的初始猜想光流为，猜想值来源于从最深处到层的光流计算。为了计算在层的光流，还需要计算出残余像素偏移（小量，满足小运动），此残差使得以下等式最小：

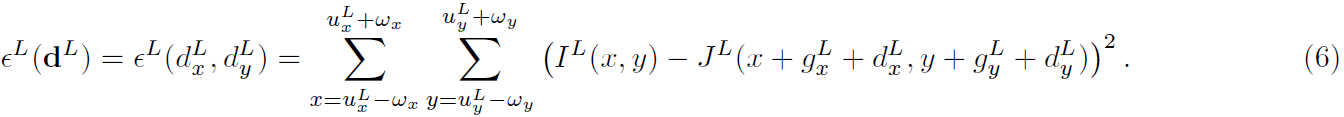
值得一提的是，在每一级中，邻域窗口的大小相同。值得注意的是，初始光流值可以被看做是对图像进行预转换：，然后由于是小量，可以看做是小运动，从而利用标准的KL算法进行求解。

由此可以看到，其思想类似于：物体运动得太快，那么利用镜头去跟踪物体，从而抵消物体运动的速度，使得两帧之间物体相对于坐标系来说是小运动。 我们研究的是一个具体的目标，如果这个目标满足三条假设，那么我们就可以采用KL光流法。镜头移动，显然对假设1和假设3是否满足是没有影响的，但是却能够改善假设2。也就是说这样是可行的！ （肯定要思考是否可以这样转换？转换之后有没有违背之前的条件？）

当求出了之后，就可以得到在层的光流为，此结果将会被传递到层，作为初始值：

依照上面的方式，直到计算到第0层，得到最终的结果。与低层对应，最高层同样有光流初始值，其值为：

设置其实就是为了增加算法更加统一，每一层计算都一样，从而可以编写循环。

最终光流为：

其亦可写作：

偏移量计算

事实上，每层的偏移量计算方式都相同，我们讨论层即可。根据公式6定义如下新的图像：

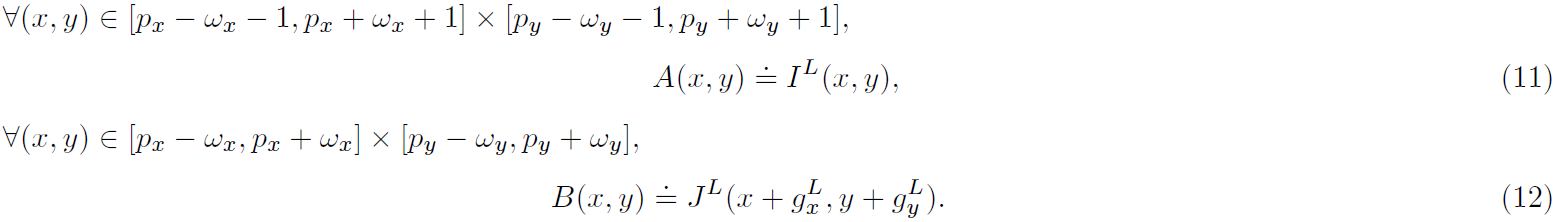
注意到，和的定义域存在差异，前者针对的邻域窗口，后者对应的邻域窗口。并记，。在新标记的条件下，我们的目的是找到使得如下式子最小：

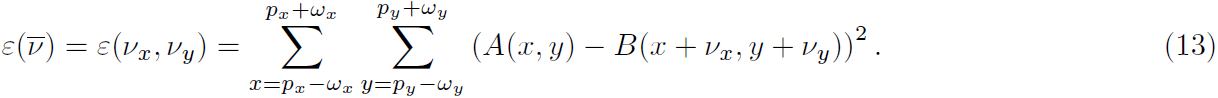
为了求取极值，需要满足一阶导数为0：

在此刻直接利用标准的LK算法，是等效的吗？

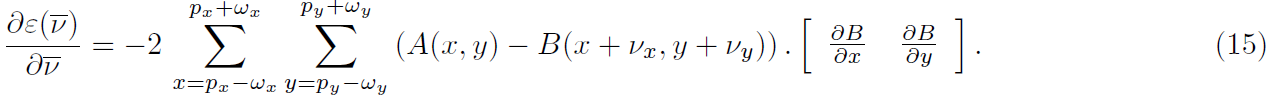
将进行泰勒展开有：，所以有：

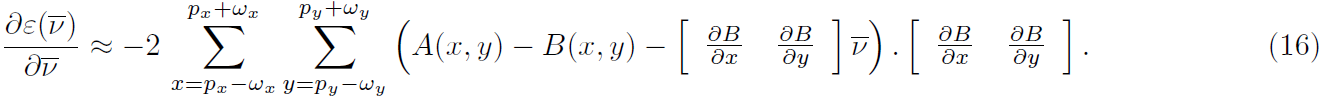
其中的可以看做是两帧之间的差分。（或者说在处的时间导数），做如下简化：

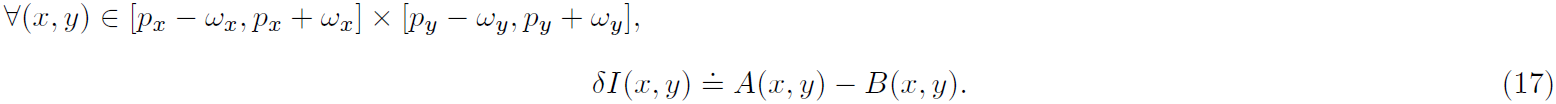
由于可以看做是时间导数，所以，可以看到其结果和标准的LK算法基本一致，但是其中的与存在差异。换言之，这两者之间是否也是等价的呢？

如果满足假设1，那么图像的梯度就能够直接用图像的梯度来代替（两个图像在指定区域内两个图像梯度完全一样）

当然在离散情况下，导数利用差分表示：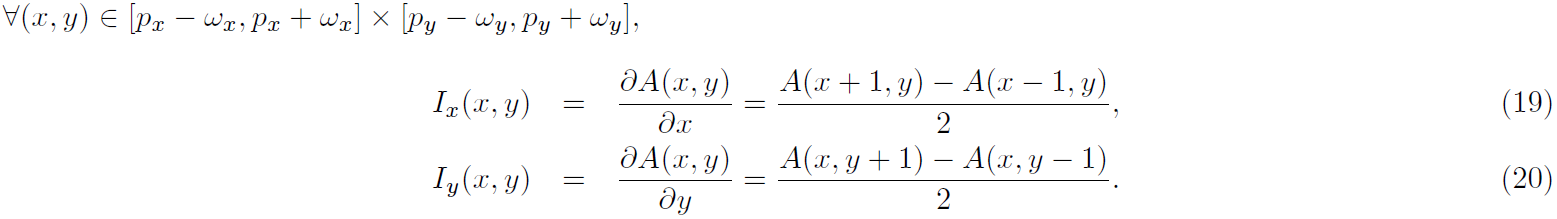

这里解释了为何，之前的定义域不同。

利用18式，代入16有：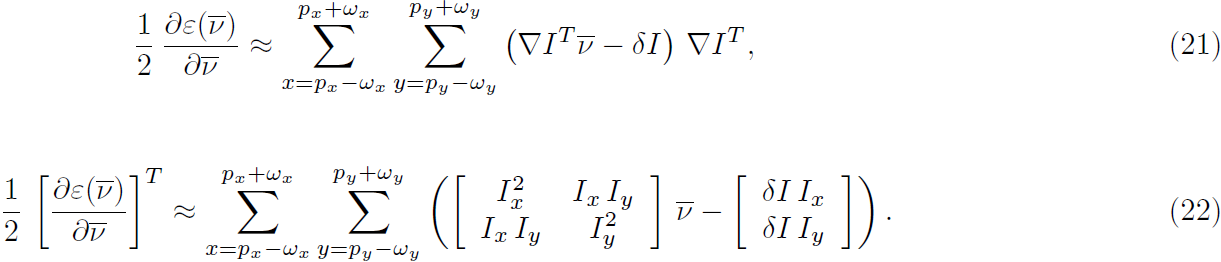

记：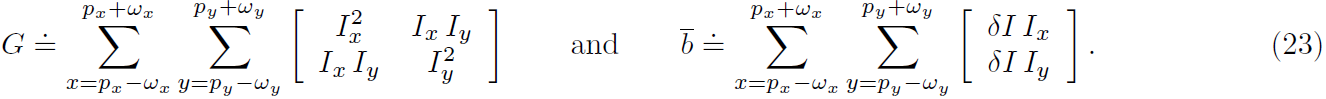

那么22简化为：

从而解得：

显然，这和标准LK算法结果相同！

为了提高精度，还可以在每一层采用牛顿迭代法的方式对光流值进行优化：每次以之前计算出来的光流值作为新的光流初始值。

后续讨论

略……

金字塔LK算法实现

后续补充

应用案例

角点

通常意义上来说，角点就是极值点，即在某方面属性特别突出的点，是在某些属性上强度最大或者最小的孤立点、线段的终点。 对于图像而言，如图所示圆圈内的部分，即为图像的角点，其是物体轮廓线的连接点。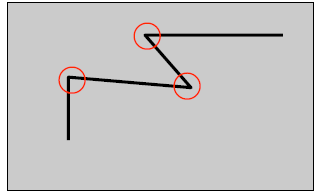

import numpy as np
import cv2
import sys
cap = cv2.VideoCapture("video.mp4")
feature_params = dict(maxCorners=100, qualityLevel=0.3, minDistance=7, blockSize=7)
lk_params = dict(winSize=(15, 15), maxLevel=2, criteria=(cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))
color = np.random.randint(0, 255, (100, 3))
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)                     # 选取好的特征点，返回特征点列表
mask = np.zeros_like(old_frame)
while(1):
    ret, frame = cap.read()
    if frame is None:
        break
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)  # 计算新的一副图像中相应的特征点的位置
    good_new = p1[st == 1]
    good_old = p0[st == 1]
    for i, (new, old) in enumerate(zip(good_new, good_old)):
        a, b = new.ravel()                                                               # ravel()函数用于降维并且不产生副本
        c, d = old.ravel()
        mask = cv2.line(mask, (a, b), (c, d), color[i].tolist(), 2)
        frame = cv2.circle(frame, (a, b), 5, color[i].tolist(), -1)
    img = cv2.add(frame, mask)
    cv2.imshow('frame', img)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)
cv2.destroyAllWindows()
cap.release()

以上代码直接调用cv2里面的方法进行角点检测及跟踪。