原论文链接 Visualizing and Understanding Convolutional Networks_2013 参考博客 可视化卷积网络

本文进行模型的可视化，从而找到对分类结果影响比较大的特征，在此基础上对模型进行调优。

当输入一张图片到卷积网中时，网络会逐级产生特征，但究竟是图片中的那一部分刺激网络产生了特定特征，没法直接得到；作者想到了一种办法：将产生的特征通过反卷积技术，重构出对应的输入刺激，而重构的刺激只会显示真正有用东西，作者就可以通过分析这些信息来分析模型，实现模型调优。

我们可以把卷积网络看成多层过滤器，它在每层不断过滤掉无用的信息保留下真正有用的信息（激活输出）。我们现在想要做的是，将被过滤的信息映射到原本的像素空间，看究竟是哪些信息激活了网络深层节点。

激活的理解：此概率来源于神经元，神经元只有在激励超过阈值才会被激活产生输出。类似Relu和Sigmoid都是来模拟这个过程的。反应到卷积网络上，通过了非线性激活函数之后的feature map就是激活后的特征。 当然，卷积网络理解方式可能存在很多版本。

Visualization with a Deconvnet

对于网络中间层的结果可视化，我们可以采取Deconvnet将其映射到输入像素空间的方法：在网络中间每层连接一个Deconvnet将其向输入像素空间进行映射。（如下图所示）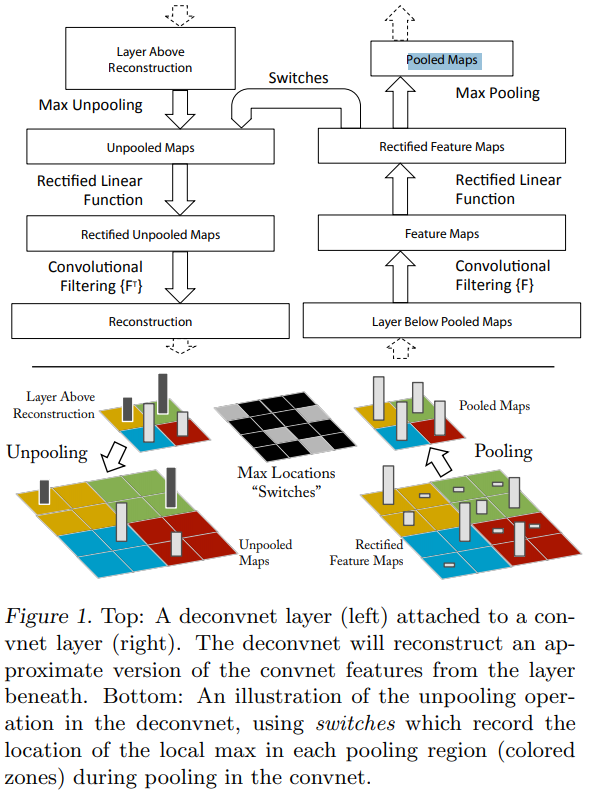
image.png

To examine a given convnet activation, we set all other activations in the layer to zero and pass the feature maps as input to the attached deconvnet layer.（啥意思？） 就是说在中间层其实有很多激活输出（feature maps），每次观察其中一个，都将未被观察者置0

在像素重建的过程中主要是重复三个操作：（1）unpool，（2）rectify，（3）filter（卷积操作）。

每次重建过程，针对中间的某一个feature map而言，所以它只是表示了中间信息的一个部分。

Unpooling

在卷积网络中，最大值池化操作不可逆，为了尽量减小误差，论文中采用了记录最大值池化过程中最大值位置的方式。在反卷积操作时，将该值放到对应的位置上，其余位置填0，实现Unpool操作。

Relu

卷积操作所有的feature maps都是正的，与之对应的重构的feature maps同样应该是正的，所以需要Relu操作。

为何在此处加？

Filter

和卷积网络采用同样的filters，但是是其转置版本。（所以Deconvnet无需学习即可得到！）

使用原卷积核的转秩和 feature map 进行卷积。反卷积其实是一个误导，这里真正的名字就是 转秩卷积操作。 在 unpooling过程中，由于“Switches”只记录了极大值的位置信息，其余位置均用 0 填充，因此重构出的图片看起来会不连续，很像原始图片中的某个碎片，这些碎片就是训练出高性能卷积网的关键。由于这些重构图像不是从模型中采样生成，因此中间不存在生成式过程。

不知道为何能够将其映射到原像素空间，因为并非逆操作啊？

参考以下博客 conv_arithmetic 转置卷积 上面的解释只是阐述了维度不变。那么其为何work？可以参考首次提出此方法的论文。（Adaptive deconvolutional networks for mid and high level feature learning） 卷积的实现是转为矩阵乘法

网络分析

网络不同层

下图展示的是不同层的feature map重构后产生的图像，左边为重构的图像，右边为原图与之对应的patch。可以看到，网络浅层主要是提取到了一些局部特征，越到深处网络激活的特征越趋于全局。比如，第二层提取到了轮廊，第三层提取到一些纹理，第四层更具区分性的特征（狗狗的脸），第五层就展示了一类物体。
image.png
image.png

数据变换

下图展示了平移、伸缩、旋转三种变换对不同层输出特征影响以及最终分类结果的影响。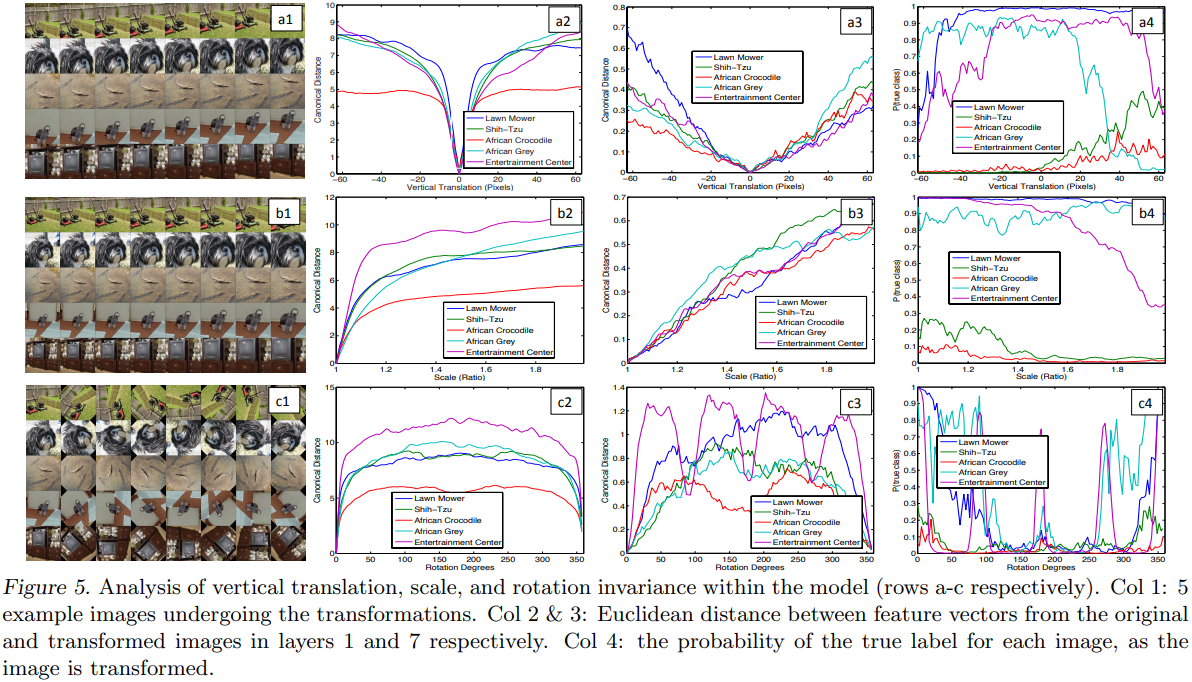
image.png
从图中可以看到：

模型结构选择

不同的卷积核大小，不同的卷积步长会产生不同的效果。
image.png
上图的(b)和(c)展示了大卷积核大步长和小卷积核小步长产生的特征差异。可以看到：在第一层小卷积核，小补偿产生的无效特征要少很多；在第二层，小卷积核，小步长的特征更清晰，混叠更少。

The first layer filters are a mix of extremely high and low frequency information, with little coverage of the mid frequencies. （如何看出？）Additionally, the 2nd layer visualization shows aliasing artifacts caused by the large stride 4 used in the 1st layer convolutions.

遮挡灵敏性

略！