IOU计算

参考：iou算法

一维情况

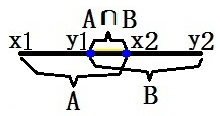
先求交集，求交集即是找到对应交集的区域的范围。
下界： IOU、AUC、ROC - 图2 上界： IOU、AUC、ROC - 图3 交集： IOU、AUC、ROC - 图4 并集：两个集合相加-交集

二维情况

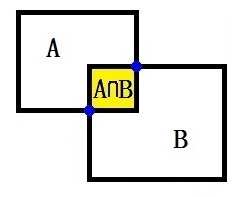
是一维的扩展，可以分别求出两个维度的交集，然后做乘法运算。
设A矩形左上角坐标为：(A1x, A1y), 右下角：(A2x, A2y)；B矩形左上角坐标为：(B1x, B1y), 右下角：(B2x, B2y)；
在x维度：
IOU、AUC、ROC - 图6
在y维度：
IOU、AUC、ROC - 图7
最终：
IOU、AUC、ROC - 图8

三维情况

与之类似。

ROC曲线绘制

https://www.jianshu.com/p/2ca96fce7e81

二分类

对于一个二分类器，其输出分类结果要么0，要么1；与此同时，输入数据的标签同样是要么0，要么1；两者进行组合可以产生四种结果：TP(true positive)、TN(true negative)、FP(false positive)、FN(false negative)

ROC 曲线横坐标是 FPR，横坐标是 TPR。其中 IOU、AUC、ROC - 图9 其中 N 表示负样本个数； IOU、AUC、ROC - 图10 其中 P 表示正样本的个数。根据定义，可以看到 FPR 和 TPR 是一对相互制约的关系。我们总是希望 TPR 越高，FPR 越低越好。但是 TPR 越高，往往意味着模型更偏向于将结果归为 P 类，那么 FPR 往往也会相应地上升；我们希望 FPR 越小，往往意味着模型需要偏向于将结果归为 N 类，从而 TPR 又会相应降低。

如何绘制 ROC 曲线呢？
原理很简单：对于一个二分类问题，假设模型输出的结果表示的含义是正类的概率。那么通过设置不同的阈值。规定概率大于阈值则归为正类，反之负类。那么这样就可以在不同的阈值下（可以从小到大，也可以从大到小。由于样本个数有限，输出的概率结果是离散的，那么往往只需要根据模型输出的离散结果进行离散取值）将当前模型预测的结果进行 FPR 和 TPR 的统计，从而得到一系列的点，这些点连接即可得到 ROC 曲线。
绘制时采用对应的 python 包即可：

from sklearn import metrics
# 真实 label
y = np.array([0, 0, 1, 1])
# 网络对正例预测的概率值
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
# 计算 auc
auc = metrics.auc(fpr, tpr)

多分类

多分类是在二分类上进行扩展，每次处理以一类为 P 类，其它类为 N 类，即可得到一系列的 AUC 曲线。
此处略。

AUC

AUC （Area Under ROC Curve）是用来定量描述 ROC 曲线的量。它表示的是 ROC 曲线下的面积。理想的模型得到的理想曲线是矩形 IOU、AUC、ROC - 图11 （黑体表示二维向量）左边和上边组成的曲线，实际模型不能达到理想模型的效果，只能取逼近它。所以曲线越偏向于左边和上边，则表示模型的结果越好，与之对应的是 AUC 值越大。